Интенсификация формирования цифровых ресурсов объектов организационной системы с учетом их геолокации, характеризующих эффективность функционирования и взаимодействия с объектами других организационных систем, создает предпосылки для формирования цифрового способа коммуникаций, с помощью которого организуется взаимодействие территориально распределенных элементов.

Применительно к социально-экономическим системам результатом этого взаимодействия является процесс влияния деятельности одной организационной системы, которую в дальнейшем будем называть основной, на деятельность других систем, в свою очередь оказывающих воздействие на основную систему. Отношения, связи и взаимодействие объектов указанных систем определяют признак их территориальной связанности [5]. Наличие этого признака позволяет сформулировать следующее определение.

66 в ыпуск 1/2020

Под территориально связанными социально-экономическими системами будем понимать совокупность нескольких систем, среди которых есть основная, объединяющая в организационное целое однородные объекты с распределенной по территории геолокацией для выполнения заданных целей, и системы, находящиеся с основной во взаимодействии как потребители результатов ее деятельности. Эффективность достижения целей по взаимодействию объектов территориально связанных социально-экономических систем определяется управляющим центром каждой системы. В зависимости от значимости объектов и уровня эффективности взаимодействия управляющие центры этих систем выделяют ресурсное обеспечение объектам основной системы [4].

Результаты анализа значимости объектов основной системы при взаимодействии с территориально связанными системами позволяют определить совокупность действий администрации и организовать интеллектуальную поддержку этим действиям в рамках следующих управленческих циклов:

• 1)    распределение объемов ресурсно-результати вн ого взаимодействия в зависимости от значимости объектов основной системы O_i , i = 1, I ;

• 2)    выбор показателей объектов основной системы f ( t , d ) , i = 1, I , j = 1, J , g 1 = 1, G j ., G j , t = 1, T , d = 1, D , оказывающих наибольшее влияние на повышение значимости i -го объекта на период перспективного планирования T + 1 1 , 1 1 = 1, T 1 ;

• 3)    управление значимостью объ ектов основной системы с учетом их принадлежности к региональным кластерам d = 1, D и выделения в рамках распределения объемов ресурсно-результативного взаимодействия дополнительных затрат на изменение выбранных показателей.

Первый управленческий цикл включает следующие действия:

• •    картографическая визуализация результатов ГИС-ориентированного мониторингового оценивания функционирования объектов основной системы с учетом показателей их результативного взаимодействия со с вяз анными межотраслевыми межрегиональными системами и подсветкой контуров d = 1, D регионов, в которых расположены объекты основной и связанных с ней систем;

• •    фиксация результатов анализа зн ачимо сти объектов основной системы O_i , i = 1, I на непрерывной шкале R i ( T + 1 1 ) , i = 1, 1 , 1 1 = 1, T 1 ;

• •    распределение объ емн ых по каз ателей результативного взаимодействия основной системы f j о ( T + 1 1 ) , j ₀ = 1, J ₀, 1 1 = 1, T 1 в виде заданий объектам основной системы обеспечивающих компенсацию от управляющего центра затрат на выполнение заданий, которые составляют основу результативного взаимодействия с территориально связанными системами;

• •    распределение затрат на рес урс ное о бес печение в рамках систе мы U_n , n = 1, N и связанных систем Z n ( T + 1 1 ) , n = 1, N , 1 1 = 1, T 1 между объектами O i , i = 1, I .

Интеллектуальная поддержка принятия управленческих решений по распределению затрат на ресурсное обеспечение функционирования объектов основной системы базируется на следующей структурированной информации:

• •    временные ряды объемных показателей результатов результативного взаимодействия основ но й сист емы со связанными на период перспективного планирования f j * ( t + 1 1 ) , j о = J , 1 1 = ГЛ;

Горячко В.В. Алгоритмизация интеллектуальной поддержки...    67

• •    временные ряды затрат на ресур сно е обе спе чение основной системы U_n , n = 1, N связанными системами Z_n ( T + 1 1 ) , n = 1, N , 1 1 = 1, T 1 ;

• •    временные ряды оценок значимости объектов основной систем ы при в заи модействии со связанными системами на непрерывной шкале R i ( T + 1 1 ) , i = 1, 1 , 1 1 = 1, T 1 ;

• •    временные ряды прогнозных оценок показателей социально-эконо мич еског о со стояния в рамках географической локации регионов f pd ( T + t 1 ) , d = 1, D , j d = 1, J d , 1 1 = 1Л;                                                ’

• •    привязка объектов основной системы к географической локации регионов O id , i d = M d , U I d = I .

d = 1

Интеллектуальная поддержка принятия управленческих решений с использованием перечисленных структурированных информационных ресурсов осуществляется на основе параметрической схемы распределения ресурсного обеспечения.

При распределении объемных показателей результативного взаим одей ствия с учетом потребностей объектов основной системы f jpd ( T + 1 1 ) , d = 1, D , j id = 1, J d , 1 1 = 1, T 1

f o d ( T + t 1 ) = f^ ( T + T 1 H ( T + t 1 K d ( T + t 1 ) ( A - R id ( T + t 1 ) ) ,

где параметр p . о ( T + 1 1 ) определяется из условия

D I d

EE f ,-"id ( ^{T +} t 1 ) = f ( ^{T +} t 1 ) для ^всех f id - ⁰, d = 1 id _______ _______ _______ ________

• d = 1, D , i d = 1, I d , j 0 = 1, J 0 , t 1 = 1, T 1 ;

параметр p ,₀._a ( T + 1 1 ) - характеризует социально-экономические положения d -го региона.

Распределение затрат каждой n-й связанной системы на ресурсное обеспечение основной системы осуществляется с учетом потребностей объектов основной системы zn (T +11), n = 1,N, in = 1,I,

' n , 1 1 = 1, T 1

;*n(T +11)z" (T + T1 )-в'n (T +11)(A — R„), zi

где параметр β ^' _i ^' _n находится из условия

I n

E z n ( ^{T +} t 1 ) = ^Zn ( ^{T +} t 1 ) Для всех Z in ( ^{T +} t 1 ) > ⁰ , i n =1                          ________ ________ _________

• n = 1, N , i n = 1, I n , t 1 = 1, T 1 .

Структурная схема алгоритма интеллектуальной поддержки управления распределением ресурсного обеспечения между объектами основной системы приведена на рисунке 1.

Как видно из выражений (1)–(2), объем ресурсного обеспечения i -г о о бъекта основной системы из всех источников зависит от значимости R_i объекта O_i , i = 1, I или на дискретной шкале от позиции в рейтинговом списке r_i , i = 1, I . Поэтому объекты основной системы заинтересованы в выделении затрат из общего ресурсного обеспечения Z i ( T + T 1 ) с целью перехода на более высокую позицию по значимости r n ( T + T 1 ) = r i ( T + T 1 ) v , 1 1 = 1, T 1 , где V - число позиций продвижения в рейтинговом списке. Поскольку на вели-

68 в ыпуск 1/2020

чину r влияет значение интегральной оценки F i ( T + T 1 ) , которая, в свою очередь, зависит от значений показателей мониторинга f ( T + T 1 ) i = 1, I , g = 1, G , j_g = 1, J_g , то величина ν определяется увели чен ием показателей f_ijg . Среди указанных показателей есть наиболее влия тель ные m = 1, M . Именно на их увеличение целесообразно выделить средства z mi , m i = 1, M ; из общих затрат Z . .

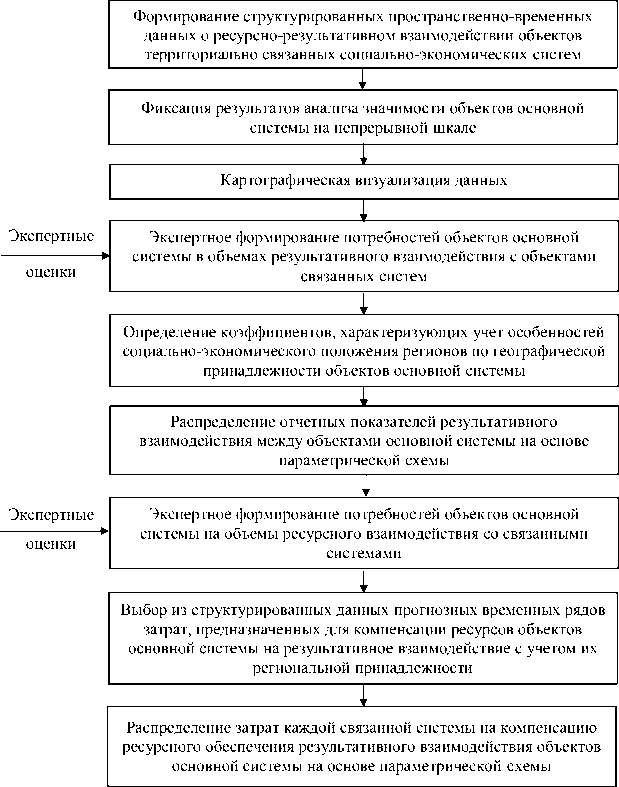
Рис. 1. Структурная схема алгоритма интеллектуальной поддержки управления ресурсно-результативным взаимодействием с учетом значимости объектов основной системы

Управление этим процессом базируется на дв ух оптимизационных задачах:

• •    выборе показателей мониторинга f_im , m = 1, M , наиболее влиятельных на изменения значимости объекта;

• •    определении таких значений z_m ^* _i , m_i = 1, M_i при распределенном ресурсном обеспечении объекта основной системы, при которых происходит продвижение на дискретной шкале значимости на ν позиций.

Управленческий цикл в рамках первой задачи включает следующие действия, обеспечивающие интеллектуальную поддержку принятия решений:

• •    формирование оптимизационно й м одели;

• •    ранжирование показателей j_g = 1, J_g , входящих в каждое g -е, g = 1, G направление мониторинга, и вероятностная интеграция рангов;

  Горячко В.В. Алгоритмизация интеллектуальной поддержки...    69

  
  

  • •    интеграция вероятностной интеграции рангов и рандомизированного поиска решения оптимизационной задачи;

  • •    фо рми рование множества доминирующих вариантов набора влиятельных показателей m = 1, M и экспертный выбор окончательного варианта.

    70 в ыпуск 1/2020

  Для формирования оптимизационной модели введем булевые оптимизируемые переменные:

  
  

  x_i

  
  

  1, если показатель f_jg включается в набор влиятельных показателей m = 1, M ,

  0 в противном случае,

  
  
  
  

  j = 1, J , g = 1, G . j_g , _g , g , .

  Задача состоит в минимизации числа показателей, входящих в набор m = 1, M :

  G = 1 J g

  EE x ig ^ min.

  
  
  
  

  При этом необходимым условием является то, чтобы из каждого направления мониторинга в число влиятельных показателей вошло не менее одного показателя

  J g

  
  

  где c jg

  
  

  E ^c«^xig ^ 1, g = 1, G , j_t = 1

  1, если в показатель f_jg относится к g -му направлению, 0 в противном случае.

  
  
  
  

  Объединяя критерий оптимизации (4), ограничения (5) и требования к оптимизируемым переменным (3), получаем следующую оптимизационную модель:

  
  

  G J g

  EE x ig ^ min.

  
  
  
  

  J g

  X c jg x g ^ ¹, g = ¹, G ,

  j g ^{= 1} f l, x ig =j 0, j g = ¹, J g , g = ¹, G .

  Второе дейс тви е состоит в проведении экспертного априорного ранжирования направлений g = 1, G мониторинга показателей f_ig по каждому направлению по степени их влияния на возможность перехода i -го объекта основной системы на более высокую позицию в рейтинге [2]. Получим значения a_g , принимающие значения от 1 до G , и значения a_jg , принимающие значения от 1 до I_g . Проведем вероятностную интерпретацию рангов в виде вероятностей, которые будут использоваться на первом шаге k = 1 рандомизиро-

  
  

  ванного поиска решения задачи (6):

  P g =

  
  

  1/ a_g

  
  

  p xjg

  
  

  G ,

  ^E g . , 1/ a .

  1/ a jg

  
  

  E ': = ,/ a.'

  
  

  G

  E p g = i;

  g . 1

  J g

  E p X «= i.

  j g =

  
  
  
  

Поскольку от значений (7) зависит эффективность поиска [2], интегрируем их в рандомизированную схему для определения вероятностных параметров на к = 2, 3, . . итерациях:

pk, 1=pkg. + ж (А«т (x.)), (8)

p‘ g + 1 = p g ⁺ ® 2 (^Д jg ^Т ( x jg ) ) , ⁽⁹⁾ где ж . ( • ) , ж ( • ) - функции преобразования вариаций эквивалентной задачи оптимизации A jg Т при случайных значениях переменных x c jg [3].

В результате при заданном числе итераций K получаем наборы со значениями x^K_jg = 1 или 0, из которых, в зависимости от величины вероятностей (8)–(9), выбираем 5–7 доминирующих вариантов [Там же].

Окончательно выбирается вариант на основе экспертного ранжирования [2] и определения варианта с наименьшим рангом. Значения x^K_jg = 1 определяют т е п оказат ели, которые включаются в набор влиятельных показателей для объекта O_i , i = 1, I , m_i = 1, M_i .

Структурная схема алгоритма интеллектуальной поддержки управления выбором показателей, влияющих на повышение рейтинга объекта основной системы, приведена на рисунке 2.

Решение второй задачи рассмотрено в [1].

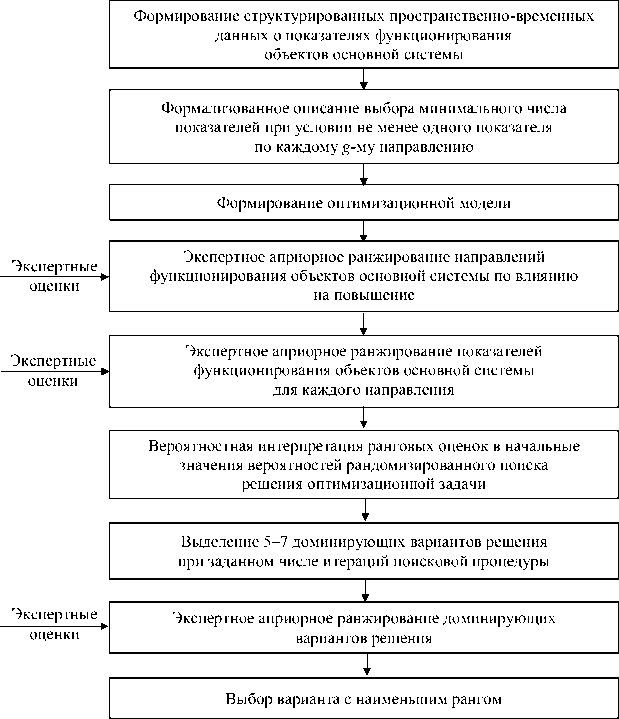
Рис. 2. Структурная схема алгоритма интеллектуальной поддержки управления выбором показателей по влиянию на повышение рейтинга объекта основной системы

Лисицкий В.В., Калинин Т.В., Миганов А.Г., Столбов А.В. Метод распределения...    71

Целевым результатом алгоритмов интеллектуальной поддержки принятия управленческих решений с использованием оценок значимости объектов основной системы при взаимодействии с территориально связанными социально-экономическими системами являются эффективные управленческие действия по распределению объемов ресурснорезультативного взаимодействия, выбору показателей объектов основной системы, оказывающих наибольшее влияние на повышение их значимости, а также достижению объектами основной системы более высокого уровня значимости в рамках взаимодействия с управляющим центром и связанными системами с учетом региональной принадлежности.