Алгоритмы и программное обеспечение для моделирования импульсных процессов

В статье рассмотрены вопросы разработки и программной реализации разностных схем для численного моделирования процессов импульсного деформирования твердых тел.

Для моделирования этих процессов построена математическая модель и алгоритм решения задач динамического деформирования. Задача может рассматриваться в различных постановках – осесимметричная, плоское напряженное состояние, плоское деформированное состояние.

Алгоритм предусматривает использование различных конечно-элементных сеток (регулярных, нерегулярных, смешанных, сформированных в других пакетах). Элементы могут быть 3-угольные, 4-угольные. Конечно-разностная схема реализована в виде алгоритма "поэлементной сборки", что повышает ее эффективность, а также позволяет применять распараллеливание.

Рассмотрены три основные задачи динамического деформирования тел при импульсном нагружении – удар деформируемого тела о жесткую стенку, осадка образца, деформация тела под действием приложенного внешнего давления. Реализованы три модели поведения материала – упругая, упруговязкопластическая модель, модель грунта.

Разработан препроцессор для оперативного выбора геометрических и силовых параметров задачи, модели материала, необходимых схемных параметров. Решение задач выполняют исполнительные модули. Результаты могут быть представлены в виде деформируемой области и напряженно-деформированного состояния тела в различные моменты времени, усилий в зонах контакта с преградой или поверхностями пресса.

В статье приведены результаты численных расчетов и дано их сравнение с экспериментальными данными. Особое внимание уделено оценке влияния схемных параметров, зависящих от типа конечного элемента, на результаты решения.

• 2.    Уравнения движения

Рассмотрим уравнения движения и их конечно-разностную аппроксимацию на примере осесимметричной задачи, что не нарушает общности рассуждений (рис. 1). Движение рассматривается в плоскости, проходящей через ось симметрии Oz , и считается не зависящим от угловой компоненты.

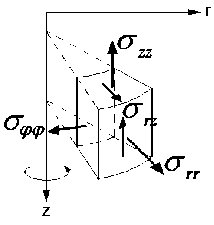
Рис. 1 . Схема для осесимметричной задачи

Запишем уравнения сохранения им пульса [1-3]:

p v z

дагг да а zz          zr        zr дz     д r     r а + а +а -а дz    д r       r

Здесь р - плотность среды; vz, vr -компоненты вектора массовой скорости по осям Oz и Or; а - компоненты тензора напряжений Коши. Система уравнений (1) описывает движение материальной частицы среды в эйлеровой системе координат под дейст- вием тензора напряжений aij.

Компоненты тензора скоростей деформаций связаны со скоростями частиц диффе- ренциальными зависимостями Коши

.    д vz       .    д vr      .

zrr

^zz          ,    ^rr ~   ,   £фф,

Оz          О rr

.    1 ( д v_z

£„ =— —— +-

2 уд r    д z у

Для построения численной схемы выполняется дискретизация области, т.е. строится конечно-элементная сетка, а затем для каждого J -го узла сетки формируется конечноразностное уравнение движения для компонент скорости и координат.

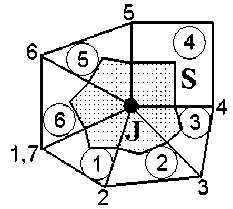
Рис. 2 . Область интегрирования S для J -го узла

Для получения разностных уравнений интегрируем уравнения (1) по площади S (рис. 2).

Поскольку рассматривается осесимметричная задача, выделим в правой части интегралов недивергентные ~, wr и дивергентные части. При этом полагаем, что за один шаг по времени движение считается "замороженным", т.е. величины в каждом элементе по- стоянны.

В результате для компонент скорости получены соотношения

„•- w z х ¹ k k -H-,T⁽ k J v z        + ^1/ / j ^{[ а} zz ⁽ r k +1 r k ) ^a zr ⁽ z k +1 z k^{) ]}

M,  ² M j k =1

j

V•= w-            cr(k)(r            k)(z -z A vr M. 2MJ y^zr (rk+1 rk) arr (zk+1 zk)]

Mj = NS [pkAj], k=1

~   NS (azr)~ Ns kr -a^^}AAkj wz = У        ,  wr = У.

^k = 1   ⁽ r s ) k               ^k = 1       ⁽ r s ) k

Здесь k - номера ячеек, окружающих узел j ; NS - число элементов, окружающих узел J ; ( p , a ij ) _k - плотность и тензор напряжений в k -й ячейке; A _k j - площадь части S конечного элемента, окружающая узел j ; ( r \ - r -координата геометрического центра элемента.

Суммирование производится по всем элементам, окружающим узел J (рис. 2, 3).

Закон сохранения импульса выполняется точно, если узел сетки является центром тяжести его "звезды". Закон сохранения массы разностной аппроксимации не подвергался, поскольку для рассматриваемого конечного элемента он выполняется автоматически в силу лагранжевого подхода к описанию среды и отсутствия потоков массы через ребра ячеек.

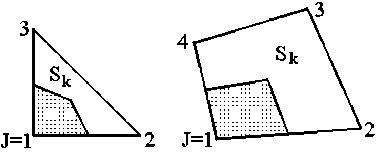
Рис. 3 . Вклад k -го элемента в область интегрирования для J -го узла

Для оптимального вычисления правой части в (3) при интегрировании (1) по области S используется метод поэлементной сборки по всем элементам (1 v Ne). Для этого вводят ся понятия узловых усилий и узловых масс:

Ne                      Ne

F j = X ( A F Z ) jk 3 _jk , F j = X ( A F П )_jk 8 _jk , k = 1                              k = 1

Ne

M n E \ M . ^ . , 8 jk = {1, j e e k ; 0, ^ }. k = 1

Каждый узел J (рис. 3) в конечном элементе k окружает часть площади Sk всего элемента, которая будет определять соответствующий вклад в узловые силы и массы. Эта площадь ограничена линиями, соединяющими середины прилежащих сторон и геометрический центр элемента.

На рис. 3 для узла 1 показана площадь Sj = Ak j, а на рис. 4 - соответствующие площади для всех узлов данного элемента k: в треугольнике - это A , A , A , в четырех- угольнике - Ak 1, Ak2 , Ak3 , Ak4

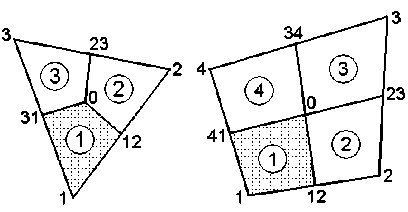
Рис. 4. Схема поэлементного вклада при вычислении усилий и масс

Соответствующий вклад в узловые силы и массы, например для локального узла 1 треугольного элемента k , имеет вид

( a f; \_к= К ( Г 31 - r j - ^ ( z 31 - z j +

, ^G zr A k 1 -i n

( I s ) k     ’

( A F r )1 k = ^[ ^ zr ^{( r} 31 - ^r 12 ) - ^ rr ^{( z} 31 - ^z 12 ) ⁺

⁽ ^ zr   ^ff ) Ak 1 n_n

( rs ) k            ’                  '

A M Ik = ^{[ p} k A k 1 ^] .

В результате, с учетом центрирования по двум временным слоям, обеспечивающим 2-й порядок точности, получены разностные соотношения

• -    для компонент скорости:

( V z ) ” ^{+ 1/2} = ( V z ) ” ^{- 1/2} +A tⁿ • ( F z ) ” / M ” ,

( V r ) ” ^+1/2 = ( V r ) ” ^{- 1/2} +A t ” • ( F r ) ” / M ” ;

• -    для координат узлов:

n + 1       n . A. n + 1/2 /    \ n + 1/2

zj  = zj+A t     • (vz ) j, n +1      n        n+1/ 2         n+1 / 2

rj   = rj +A t     • (vr ) j.

Шаг по времени определяется из условия устойчивости [3]

f A x ^{( e} ) 1

At = min

( e ) { L • C 0 J

„        .(

Здесь Axv 7- характерный размер элемента (минимальная высота в треугольнике или половина диагонали в четырехугольнике), L - число Куранта, Co - скорость звука.

• 3.    Физические уравнения

Рассмотрим для краткости только модель упруговязкопластичного материала (металлы).

Пластическое течение и объемная сжимаемость рассчитываются независимо [3]. Объемная сжимаемость, согласно принятому подходу, описывается зависимостями среднего давления от текущей плотности. Взаимовлияние может осуществляться через зависимость условия текучести от давления.

Компоненты тензора скоростей деформаций s’ связаны с компонентами скорости vi дифференциальными соотношениями Коши (2), а компоненты тензора деформаций sij определяются интегрированием соответст- вующих компонент тензора скоростей деформаций для данной материальной частицы.

Вычисление скоростей деформаций в элементе производится с использованием разностной аппроксимации. Для получения разностных соотношений используется интегральное представление частных производных. С учетом центрирования переменных по времени для треугольного элемента в момент t _H+1/2 получены соотношения

5z1г

Т =    [vz 1 (r2 - ra)+ vz2 (r3 - rl) + vz3 (ri - дz2 дz * дr

= ^ ^[ v z 1⁽ z 2

^{2 z} 3 ) ⁺ v z 2^{( z} 3 ² z i ) ⁺ v z 3⁽ z l ² z 2 )1(8)

^ =    [vr 1(r2 - r3) + vr2 (r3 - rl) + vr3 (rl - дz2 дr2

T =     [ v r 1^{( z} 2 ^{2 z} 3 ) ⁺ v r 2 ⁽ z 3 ² z 1 ) ⁺ v r 3^{( z} 1 ^{2 z} 2 ) 1

д r2

Отсюда скорости деформаций

.    дz ’     .    д r ’     .    1  д z ’     д r ’

^zz = -7-, ^ rr = -7-, ^ zr = ^(^ ⁺ V") . ⁽⁹⁾ д z         д r       2   д r    д z

Тогда новые значения деформаций

$ ^{+ 1} = ^ + А_£ ” ^+1/2,          (10)

где A = A_{n+l /2}- площадь элемента в момент t n + 1/2 , tei ^{+ 1/2} = ^ &n + 1/2 ^- приращения деформаций, A t _{n+1 /2} - шаг по времени.

Для 4-угольного элемента получены соответствующие соотношения. Численные расчеты для 4-угольных сеток показали, что при значительном деформировании элементов разностная схема теряет устойчивость, так как увеличивается погрешность при определении скоростей деформаций. Поэтому для определения скорости деформаций в 4-угольном элементе выбрана следующая схема.

В элементе находим 2 треугольника по принципу короткой диагонали, определяем в них скорости деформаций, а затем усредняем по площади. Расчеты подтвердили правильность этого подхода.

Для определения тензора напряжений с учетом упруговязкопластических свойств среды нужно определить интенсивность деформаций сдвига eU = (3 / 2)e;jeij , при- ращение A eU и скорость пластической деформации eU• =/3/2)eP• ej• = [AeU / At]n+1/2.

Тензор напряжений представим в виде суммы шаровой и девиаторной составляющих a = PI + S, (11) где I - единичный тензор, S - девиатор тензора напряжений, P - среднее давление.

Для повышения устойчивости вычислений a i ^{+ 1} определяется с учетом того, что интенсивность деформаций, скорость интенсивности пластической деформации и температура берутся с полуцелого временного слоя tn + 1/2 .

Пластическое течение материала описывается моделью упруговязкопластической среды [1, 2]. Условие текучести записывается в форме Мизеса с пределом текучести as, зависящим от деформации, скоростей деформаций и температуры. Согласно [1] запишем эту зависимость в виде as (eU ’ eU ’ 0) = a0 (6,) • [ae (eU)+ aM (ep)], (13)

где a e ( e U ) , a ^ ( e U ^j ) , a_g ( 0 ) - функции, учитывающие деформационное упрочнение, вязкое упрочнение, температурное разупрочнение.

Деформационное упрочнение представляется зависимостью [1]

a e ( e U ) = a S0 [1 + k s (1 2 exp( 2 b_se j ))] ,  (14)

где ks « 0,25 ; bs = 25 - параметры модели, подбираемые при описании экспериментальных кривых a (^) для статических испыта ний при нормальной температуре; as - ста- тический предел текучести.

Для вязкого упрочнения применим ап- проксимацию [1]

Р • ^av ^{( e} u ) =

0 P^a s

( (7 ■ x )/б ) ^Х ,

где р , х - экспериментальные параметры материала, x = lg( e U • ) е [1; 6].

Данные многочисленных испытаний показывают существенное изменение деформационных и прочностных свойств металлов при повышенных температурах. Зависимость предела текучести от температуры аппроксимировали функцией [1]

⁰ в ^{( О )} = expl П • ( 7 , • О ! 0 p ) s ^{0 ]}, (16) где О - абсолютная температура; в _р - темпе

Связь между гидростатическим давлением и текущей плотностью описывается нелинейной зависимостью, состоящей из двух ветвей:

ратура плавления; щ , п , ^s _e — параметры мо

P^{n + 1} = max{ - K ln( ^Р - 1); A ( ^Р ) ” p - A }, (19) Р о        Р о

дели.

где K - модуль объемного сжатия; A, п_р -

Предполагается, что влияние температуры на предел текучести при больших скоростях деформации подобен ее влиянию при процессах деформирования, близких к статическим.

Температура определяется из уравнения баланса энергии за счет пластического деформирования. Влияние объемной сжимаемости для средних скоростей удара (до 1 км/с)

модуль и показатель адиабаты для данного материала.

Второе соотношение в (19) справедливо при больших давлениях, достигаемых при распространении ударных волн.

Для сглаживания разрывов в схемах

не превышает 50-600 С. Разностный аналог уравнения баланса энергии имеет вид

сквозного счета введена искусственная вязкость q ” ^{+ 1/2} [3], вычисляемая только при сжа-

тии материала:

О

n + 1

n    0 : ^{+ 1} ( e u , О , e U • ) ( д e u ) n ^{+ 1}/²

О +--;=----------------

Л р ” ^{+ 1} C v

, (17)

q

” + 1/2

= ^ -

P o A [a d q

V I V I )

-

_ I ~ q L P o C 0^ A

V

V’

V

” + 1 / 2

где е_у - теплоемкость.

Девиатор напряжений вычисляем по закону упругости в дифференциальной форме с использованием производной Яуманна [3], так как рассматривается движение лагранжевой материальной частицы в эйлеровой фиксированной системе координат. Поскольку компоненты тензора напряжений отнесены к эйлеровой системе координат, то нужно учесть поворот материальной частицы за текущий временной шаг с помощью поправок 5 " ^{+ 1} [3].

В результате получим

где q_v , q_L - коэффициенты квадратичной и линейной искусственной вязкости, C - местная скорость звука.

В результате получаем полные напряжения a +1 = Si”+1 + P”+1 + q”+1/2 .    (21)

S ” ^{+ 1} = S ” + 2 G'( д£ ^{п + 1/2} - Д е ” ^{+ 1/2} ) + 5 ” ^{+ 1}, zz         zz                  zz              V             zz

S n ^{+ 1} = S n + 2 G '( д ^ ” ^{+ 1/2} -Д £ ; ^{+ 1/2} ) + 5 ” ^{+ 1}, rr          rr             \ rr                V /       rr ,

S”+1 = S” + G '(де”+1/2)+ 5”+1, zr          zr          у zr J zr ,

S

” + 1 pp

Sn zz

-

n

Srr ,

где Де ” ^{+ 1/2} = DV" ^{+ 1/2} /3 - изменение объемной деформации; G' - модуль сдвига материала.

В ходе вычислений проверяется условие текучести (12), которое отражает ограниченность девиаторных компонент тензора напряжений 0 _u ( e U ^{+ 1} ) . Если в пространстве напряжений мы выходим за пределы упругой области, то вычисленные по закону упругости компоненты девиатора тензора напряжений "переносятся" по нормали на поверхность текучести [3].

4. Граничные условия

Граничные условия в задачах соударения, проникания и действия взрыва на грунтовые массивы и элементы конструкций делятся на кинематические, динамические и смешанные [1-3].

Кинематические условия (на части поверхности S заданы перемещения или скорости) реализуются на поверхностях жесткой заделки, осях и/или плоскостях симметрии.

Динамические условия (на части поверхности S заданы поверхностные нагрузки) реализуются на свободных поверхностях, поверхностях с заданным внешним давлением.

Смешанные условия (на части поверхности S заданы одновременно и перемещения (скорости) и поверхностные нагрузки) реализуются на контактных границах (деформируемое тело - продукты детонации, деформируемое тело - жесткое тело, деформируемое тело - деформируемое тело).

Температурные эффекты на контактных поверхностях не учитываются.

Отметим, что граница контакта тел заранее неизвестна и определяется в ходе решения задачи, т.е. может возникать изменение типа граничных условий. Например, точки ударника и преграды могут находиться в контакте либо отходить от границ, тогда они считаются свободными. Указанные особенности обусловливают необходимость постоянного контроля геометрической близости точек ударника к границе преграды, и наоборот.

• 5.    Программный комплекс для моделирования импульсных процессов

Программный комплекс реализован в программной среде Compaq Fortran и Delphi; он состоит из препроцессора, модуля выбора из БД и корректировки физических параметров материала и набора исполнительных модулей, выполняющих решение задачи импульсного деформирования.

Препроцессор в интерактивном режиме выполняет выбор задачи, математической модели, параметров (физические, экспериментальные, схемные, конечно-элементную сетку), формирует для исполнительной части входной текстовый файл *.tm1 . На рис. 5, 6 приведены две начальные формы препроцессора (выбор задачи, параметров).

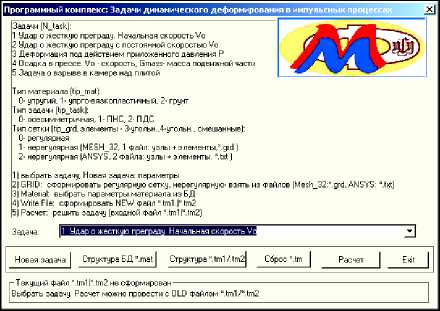
Рис. 5. Начальная форма препроцессора

Параметры модели материала выбираются из соответствующей базы данных (БД) и редактируются. Выполнена стандартизация создания и корректировки БД, что позволяет использовать в расчетных модулях различные модели материалов, при этом не внося изменений в препроцессор. Это позволяет постоянно модернизировать программный комплекс, вводя в него новые модели.

Конечно-элементные сетки могут быть построены препроцессором (регулярные сетки) или взяты из текстовых сеточных файлов, полученных в ANSYS [4] (2 файла *.txt ) или MKE_MТДТ/ Mesh_32 [5] (файл *.grd ).

В сеточных файлах предусмотрены все форматы матрицы конечных элементов: старый формат – [ i, j, k) ]; стандартные форматы ANSYS – [ i, j, k, k ]; [ i, j, k, 0 ]; [ i, j, k, l ] .

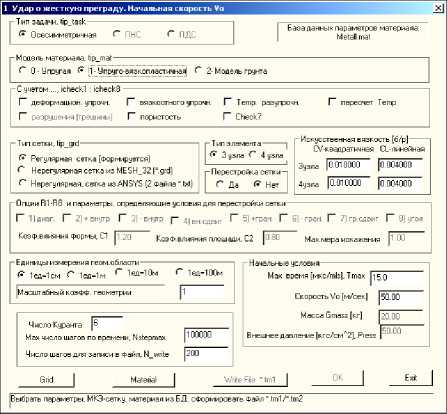
Рис. 6. Форма выбора параметров

Точность решения зависит от качества деформируемой сетки, поэтому в исполнительных модулях предусмотрен оперативный режим перестройки треугольной сетки [1]. Для каждого элемента определяется мера искажения ^ = С₁ ^ + С₂ ^₂ эталонного элемента. Здесь C , C – константы влияния формы и площади. Правильный выбор предельного значения меры искажения ц_й , C₁ , C ₂, а также коэффициентов искусственной вязкости для треугольных (CL3,CV3) и четырехугольных (CL4,CV4) элементов позволяет получить решение, достаточно хорошо согласующееся с экспериментом.

Процесс решения сопровождается периодической визуализацией сетки деформируемого образца, записью промежуточных и окончательных результатов (НДС) в текстовые файлы (*.res,*.msh ) для последующей графической визуализации постпроцессором. На каждом временном шаге в текстовый файл *.txt записываются номер шага N ; текущее время T (мкс); укорочение L/L₀ (см); текущая скорость V (м/сек); усилие в зоне контакта для последующего построения графиков и анализа решения задачи.

• 6.    Примеры работы пакета программ

В качестве одной из задач импульсного деформирования рассматривается задача соударения упруговязкопластического цилиндра с жесткой стенкой. Эта задача является классическим тестом двух- и трехмерных схем для решения задач импульсного деформирования тел. Численное моделирование задачи соударения позволяет определять параметры моделей на основе сравнения с экспериментальными данными [6].

Расчеты проводились на треугольных и четырехугольных сетках для материалов: дюралюминий, тантал, уран, бериллий, сталь. Приведем некоторые результаты. На рис. 7 показаны результаты расчета соударения деформируемого цилиндра с жесткой стенкой при различных начальных скоростях удара. Расчеты выполнялись на разных сетках, при разных свойствах материала, скоростях удара.

Сравнивалась величина укорочения цилиндров после удара. Получено совпадение результатов в пределах 7% для всех пяти металлов во всем диапазоне скоростей.

Рис. 7. Начальная и конечная форма цилиндра при ударе с различными скоростями (169м/с, …)

ления θ = 1400⁰С; статический предел текучести σ^o = 0,9 ГПа.

s ,

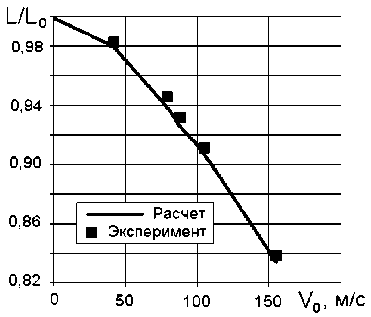
Рис. 8 . Укорочение урановых цилиндров при ударе с различными скоростями

Были проведены расчеты удара бериллиевым цилиндром на различных сетках (регулярных треугольных, регулярных четырехугольных, смешанных). Данные сравнения приведены в таблице. Наблюдается хорошее соответствие расчетных данных, что говорит о возможности применения сеток различной структуры для расчета импульсных процессов.

Результат расчетов удара на разных сетках

V 0 (м/с)	L/Lo (эксперимент )	Расчет L/Lo на различных типах сеток
		▲	■	▲+■
158	0,970	0,966	0,961	0,965
181	0,963	0,958	0,953	0,956
203	0,958	0,953	0,947	0,951
205	0,953	0,947	0,940	0,945
273	0,932	0,925	0,917	0,922

На рис. 8 сравниваются расчетные и экспериментальные [6] величины остаточного укорочения L / L ₀ уранового цилиндра. Параметры материала: удельный вес γ = 18,7 гс/см³; объемный модуль K = 210 ГПа; модуль сдвига G = 80 ГПа; модуль адиабаты A =20 ГПа; показатель адиабаты n_p = 5,8; теплоемкость C_V = 0,96Кдж/кг·К; температура плав-

На рис. 9 представлены результаты расчета соударения полой сферы и полого цилиндра с жесткой стенкой. Сетки инкорпорированы из пакета ANSYS [4]. Показаны начальная (слева) и конечная (справа) конфигурации. Рисунок иллюстрирует возможности расчета динамических задач на сетках произвольной структуры, что позволяет рассматривать тела произвольной формы.

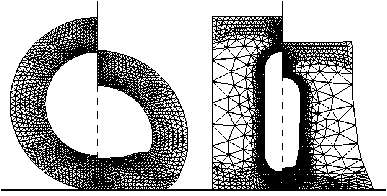
Рис. 9 . Расчет соударения сферы и цилиндра на сетках, сформированных в ANSYS

Пример расчета динамической осадки неоднородного образца в плоской постановке приведен на рис. 10.

Рис. 10 . Расчет динамической осадки образца

• 7.    Заключение

Разработан программный комплекс для решения различных задач импульсного деформирования твердых тел в двухмерной постановке. Показана возможность использования регулярных и нерегулярных трех- и четырехузловых сеток.

Выполнены численные эксперименты для сравнения с экспериментальными данными, на основании которых определены параметры модели для пяти металлов. Определены оптимальные схемные параметры (коэффициенты искусственной вязкости, параметры перестройки сетки и т.д.).

Проведены расчеты, которые показали, что каждый тип сеток оптимален для своего класса задач и условий деформирования.