An Integrated Approach to Drive Ontological Structure from Folksonomie

Published Online November 2014 in MECS DOI: 10.5815/ijitcs.2014.12.05

/* look for the tag in WordNet*/

• 7                 if not Exist then

• 8                  end if

• 9    tag =Stemming(tag)

  /*The stemming task reduces tags to their stem or root*/

• 10           end if

• 11   CleanDataSetFile.add(Tag)

• 12    end while

• B.    Preparation of tags

In this step, we generate a list of tags in their generality order and a vector space representation of tags. The generality degree is based on the FDU measure that counts the frequency of use of a given tag by distinct users. The vector space representation is based on an ameliorated version of our proposed similarity measure CDU (Co-occurrences in Distinct Users). Although this later outperforms the Co-occurrence measure and ameliorates results when used as the basis to calculate other similarity measures as the cosine one, it suffers from having non-normalized values, so that it cannot be the input for other steps such as clustering and hierarchy extraction. These steps are based on comparison between similarity values that require to be normalized. In the prior work, we tackled this problem by calculating the cosine similarity matrix using the CDU matrix. We call this new version of similarity measure NCDU (Normalized CDU).

Before describing the FDU and NCDU measures, we first give a definition of folksonomy and its elements.

Definition 1: Folksonomy

A folksonomy is defined as a tuple F = { T , U , R ,7} , where T is the set of tags that comprise the vocabulary expressed by the folksonomy; U, R are respectively the sets of users and resources that annotate and are annotated with the tags of T; and Y = {(it, t , r )} e U x T x R is the set of assignments (annotations) of each tag to a resource by a user u.

A post is a triple (u,t_ur,r ) with и £ U, r £ R and anon-empty set t_ur = { t ET \ (u,r,t ) £ Y } .

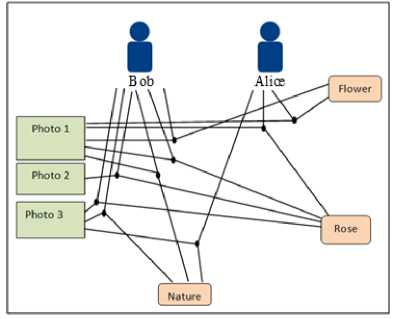
Fig. 2. An example of a folksonomy

Fig. 2 displays an example of a folksonomy. In the following, we use this running example to illustrate the proposed measure.

Generality measure: A first natural intuition is that the more general tags are simply the more often used ones, since they are well known by users. We capture this intuition in the generality measure “FDU”.

Definition 2: FDU generality measure

The FDU generality measure is an adapted version of frequency that counts number of distinct users annotating resources with a given tag. Formally, we define it as follows:

∀ t, ∈ T , u ∈ U,FDU ( t )= card, {( и ) ∈ U | t ∈ tur }  (1)

Below, we report the resulting similarity FDU values of the example.

Table 1. The resulting FDU values

Tags	Flower	Rose	Nature
FDU	2	2	2

Similarity measure: As measures for relatedness are not well developed for three-mode data such as folksonomies, we need to narrow triples by one. Various solutions have been proposed to calculate similarities between tags and resources based on two-mode views of the data [25]. Unlike the prior work where we used the macro-aggregation solution, in this paper we use a tag-tag binary representation for each user instead of the tagresource representation, then we aggregate across users. This representation ameliorates runtime performance, because the resources’ number is significantly bigger than tags one (especially after the cleansing task), so the tag– resource representation necessitates more space memory and calculating time.

The values of the tag-tag per-user binary representations are w (t 1 ,t2) ∈ {0.1 }, where t 1 and t 2 are pairs of tags.w (t ,t2)=0 means that t1and t 2 do not appear together in any post associated to the user “u”.w (t Y ,t2)=1 means that t₁ and t₂ co-occur at least once in the posts of the user. Formally :

∀ (tl , t₂) ∈ T , u ∈ U, r ∈ R

WM (tl , f2)={1

if ∃ ^ur ∶ (tl , t2 ) ∈ tur

0 else

For the folksonomy example in Fig.2, the binary representation is shown in Table 2 and Table 3 for the users Bob and Alice respectively.

Table 2. Bob’s binary matrix

Tags Tags	Flower	Rose	Nature
Flower	-	1	1
Rose	1	-	1
Nature	1	1	-

Table 3. Alice’s binary matrix

Tags Tags	Tags	Rose	Nature
Flower	-	1	0
Rose	1	-	0
Nature	0	0	-

NCDU is an ameliorated version of CDU. It is calculated by summing the binary matrix across users, then dividing on the smallest generality degree of each pair of tags. The advantage of this second version of CDU is not restricted only on considering the three modes of a folksonomy all at once, but also on generating normalized and more accurate values of similarity.

Definition 3 : NCDU Similarity measure

The NCDU similarity measure is an adapted version of CDU. Formally, we define it as follows:

∀ t1, t2 ∈ T , u ∈ U, r ∈ R:

NCDU ( ti , ti )=    ^∑ u^ ( , h                   (3)

(      (   ),      (   ))

Below, we report the resulting similarity matrix NCDU in table 4.

Table 4. The resulting NCDU matrix

Tags Tags	Flower	Rose	Nature
Flower	-	1	1/2
Rose	1	-	1/2
Nature	1/2	1/2	-

This new measure permits us to compare values easily in the step of generating the hierarchy. Moreover, it avoids calculating another matrix as cosine matrix or others. This is because of the normalization as well as the flexibility that offers our new algorithm of clustering which deals with spares matrices. This algorithm is the focus of the next section.

• C.    Context identification and disambiguation

Despite the advantages of social tags, they suffer from various vocabulary problems. Ambiguity (polysemy) of the tags arises as users apply the same tag in different domains. On the other side, the lack of synonym control can lead to different tags being used for the same concept. These problems are being investigated in the literature. There are approaches that attempt to identify the actual meaning of a tag by linking it with structured knowledge bases [22, 26].

Other works apply probabilistic models and clustering techniques on the tag space according to the tag cooccurrences in item annotation profiles [27, 28, 29].

In this paper, we follow a clustering strategy as well, but in contrast to previous approaches, our proposition provides the following benefits:

• •    Instead of using standard clustering processes, we propose to apply a fuzzy clustering technique that allows tags to belong to more than one cluster. Similar tags are belonging to the same cluster, whereas ambiguous tags are found in the intersection of two or more clusters.

• •    Instead of using simple tag co-occurrence similarity measure, we use the new similarity measure NCDU .

The literature provides many examples for context identification and disambiguation. These approaches consider hard clustering techniques as a way to assign a set of tags into distinct clusters so that tags in the same cluster are more similar to each other than to those in other clusters. This clustering task figures the meaning of tags by collecting his similar tags or his context, but supplement efforts must be perused to tackle ambiguity problem. In [22] the disambiguation activity analyzes each group of similar tags found in the context identification in order to find tags with different meanings. Benz et al [8] applied a standard average-link hierarchical algorithm [30] to disambiguate tags.

Inspired by prior work, and after having limited success-producing clusters with other algorithms, we developed Algorithm 2, a new fuzzy clustering algorithm to group similar tags into clusters and to identify ambiguous tags that belong to more than one cluster.

Algorithm 2:    context identification and disambiguation of tags

Inputs:

• -    NCDU[n][n] /*The similarity matrix of tags t₁,…,t_n*/

• -    L_generality/*a list of tags t₁,…,t_n in descending vertex order of their generality measured by FDU */

• -    min_sim/* parameter for the threshold at which a tag is chosen as a center */

Output:

• -    c /* The number of clusters generated*/

• - U[n][c] /* the membership matrix of the tags*/

• 1:    centers [0] ←L generality [0] /* add the first tag in the generality list as the first center */

• 2:    c=1 /* the actual number of clusters*/

3:i=1;    /* index of L generality */

• 4:    while igenerality.size do

  /* testing if the similarity between the new center and the othersis less than the similarity threshold to minimize the similaritybetween the generated clusters*/

5: if NCDU[L generality [i]][allcenters]then

• 6:        c+ =1

• 7:          centers[c]←L_genera li _ty[i]

8:end if

• 9:  i+=1 /* take another tag from the L generality */

10:end while

• 11:    for i=0 tot do

12: for k=0 to c do

13:U=NCDU[i][k] /* membership values*/

14:end for15:end for

• 16:    return (c, U)

We first discuss the algorithm then we offer some insight why such a simple algorithm is extremely successful. The algorithm starts by adding the first tag in the generality list as the first center (line 1), and initializing the number of clusters “c” (line 2). After that, it chooses tags from the generality list to be considered as centers. This choice is based on a similarity threshold to ensure maximizing the distances between centers (lines 4

• 1 0). Once all centers are chosen, the algorithms calculates the membership matrix to be returned with the number of clusters as outputs.

This new algorithm overcomes the limitations of the Fuzzy C-means clustering (FCM) [11] and of most of clustering algorithms. We cite these limitations below: • The number of clusters “c” must be predefined: the main disadvantage of FCM and of the majority of clustering algorithms is the obligation to define a fixed number of clusters. This task is very difficult whatever the nature of the data, and more difficult in our case because defining how many clusters can be generated when clustering a set of tags in a folksonomy is not a trivial task.

• •    The value of the fuzziness degree “m” in FCM is a prerequisite for the algorithm:   in the case of the

disambiguation task, this parameter represents how many senses an ambiguous tag can have in a given dataset. The value of this parameter is often 2, which means that no tag can have more than two different senses, and all ambiguous tags have the same meanings count.

• •    Attributing tags to clusters is based on the distance between these tags and the centers of clusters, but these centers are not effective tags, so the context of a tag is based on the other tags in the same cluster, so is not clearly defined because a cluster can have noisy tags.

• •    The results as sensitive to the initial guess, like the centers and the membership matrix, and a good choice for this guess is not evident.

• •    Clustering algorithms have mostly long computational time (complicated calculations, and lot of iterations).

Our algorithm overcomes all these shortcomings as it decides by itself the number of clusters. This is achieved by adding new centers while there are tags not classed. It also doesn’t require any value of the fuzziness parameter, so it extracts the effective number of senses that an ambiguous tag has depending on the similarity values between a tag and centers of the associated clusters. In addition, the context extracted by our algorithm for the tags is clearly defined since centers of clusters are a set of chosen tags from the folksonomy, so they can be considered as the definitions of meanings of clusters. Furthermore, unlike the other algorithms of clustering, this new algorithm doesn’t need any initial guess as it doesn’t use any arbitrary information, so the results do not change when rerunning the algorithm except if the dataset is changed.

Moreover, this new algorithm is simple and doesn’t necessitate long computational time. This will be demonstrated in the experimental section by comparing it with FCM. At the end of the context identification and disambiguation step, we have a set of overlapped clusters. The tags that belong to the intersection are ambiguous tags, and the number of their meanings is the associated clusters count. Once this step is achieved, we can generate the hierarchy of tags. This task is discussed in the next section.

D. Semantic identification

Most of the approaches associating semantic entities to tags rely on string matching techniques to find candidate ontology concepts and then use the tag context to choose the one that better describes the meaning of a tag. However, this activity implies the transition from a flat space, i.e., without hierarchies, in the folksonomy side, to a hierarchical space in the ontology side. Some works tackle this problem by associating tags initially to WordNet Synsets, and then the Synset hierarchical structure is compared against ontologies [16]. In a comparative study realized by [31], it was proven that the algorithm of Heymann et al [7] outperforms all the algorithms introduced in the study.

In this paper, we propose Algorithm 3 that extend Heymann’s algorithm by providing the following improvements:

• •    Instead of using generality measured by degree centrality in the tag-tag co-occurrence network [32] as in [8], we use FDU as generality measure. Thereby, we take the dimension of the user into account.

• •    Tags underneath the root are the centers generated in the context identification and disambiguation step.

Algorithm 3: Semantic Identification

Inputs:

• -    Lgenerality/*a list of tags t 1 ,…,t n in descending vertex order of their generality measured by FDU */

• -    nc[t 1 ],…,nc[t n ]/* The count of clusters nc[t 1 ],…, nc[t n ] where the tag is included */

• -    min_sim/* parameter for the threshold at which a tag becomes a child of a related parent rather than the root */

  - c /* the centers count*/

• -    Centers[c] /* the centers set generated in the clustering step*/

Output:

• -    Hierarchy

• 1:    Hierarchy←< root>

• 2:    for i=1 to c do

• 3:   Hierarchy←centers[i]

4:Lgenerality. Remove(centers[i]);

/* remove the tag from the generality list*/

• 5:    end for

• 6:    for i=0 to i L generaiity I do

• 7:     t i ← L g _enera li _ty[i]

• 8:    k=nc[t i ]

• 9:   maxCandidateVal ← 0

• 10:   repeat /*if t_i is an ambiguous tag, repeat steps 7

to

• 17 for each of its senses.*/

• 11:     for all t j e getVertices(Hierarchy) do

  /*identify the most similar existing tag t j to t i */

• 12:     if CDUN(t i ,t j ) >maxCandidateVal then

  /* computes the cosine similarity between ti and tj */

• 13:       maxCandidateVal ←NCDU(t i ,t j )

• 14:       maxCandidate ← t j

• 15:     end if

• 20:      Hierarchy ← Hierarchy i>

• 21:    endif

22:k=k-1

• 23:   Until k =0 /* all senses of t_i are added to the

hierarchy*/

• 24:    end for

• 25:    Return (Hierarchy)

The algorithm starts with a tree with a single node “root” that represents the top of the tree (line1). Then the centers generated by the clustering algorithm are put underneath the root without forgetting to remove them from the generality list (lines 2-5). Each tag is then added in the decreasing order of how general the tag is. The algorithm adds each tag to his most similar one in the tree if their similarity is greater than a similarity threshold (lines 7-18), else it is added under the root (lines 19-20). If the tag is ambiguous then it repeats steps 10-23 for each of its senses.

• IV.    Experiments

We perform a set of experiments in order to quantify the influence of the proposed measures of tag relatedness, and tag generality on emergent tag semantics in a folksonomy. As well as to evaluate the ability of the new clustering algorithm to define context of tags and to detect ambiguous ones. We will first provide details on our dataset and then explain each experimentation step before discussing the results.

• A.    Dataset

  We used a snapshot of the Flickr3 metadata database gathered in the period from November 24^th to December 31^th, 2005. Originally it contained |U|= 111, 920 users, |R|= 3,253,390 resources, and |T|= 374,076 tags. In the cleansing step of our approach, we choose the most relevant tags based on their frequency and their meaningfulness, as described in section 3.1. This resulted in a data set of roughly 18,329 images. The associated vocabulary has well over 6,798 terms chosen by 1,904 users.

• B.    Preparation of tags

In this step, we generate a list of tags ordered by their generality degree. The generality measure implemented is the proposed one (FDU). Table 5 and 6 depict excerpts of this list for Flickr and delicious dataset respectively.

16:end for

• 17:    if maxCandidateVal>min_sim then

  /* t j is the most similar tag to t_i*/

• 18:     Hierarchy ^ Hierarchy u i >

  /* t_i is added to the hierarchy under t j */

• 19:    else

3

Table 5. An excerpt of generality list of Flickr dataset measured by FDU

Tag	Generality degree
Food	4561
Music	1114
Sport	856
Restaurant	373
Japan	366
Transport	276
Friend	265

Table 10. Most similar 4 terms to some tags using Co-occurrence

	(1)	(2)	(3)	(4)
Architecture	Red	Fish	Travel	January
Canada	Photo	Fish	Doughnut	Drink
Art	Tokyo	June	Topv	Reflection
Fun	People	July	Team	Beer
Cat	House	France	Grill	Cookie
Band	Travel	China	Macro	Birthday
Famous	Scott	South	Brighton	Dance
Car	April	Travel	Red	Birthday

Table 6. An excerpt of generality list of Delicious dataset measured by FDU

Tag	Generality degree
Web	8680
Design	4720
Html	2950
Blog	2373
Search	2280
News	2200
Art	1290

Table 7. An excerpt of the NCDU Matrix

	Food	Girl	Airline	Music	Sport
Actress	0,00	0,67	0,00	0,33	0,00
Adventure	0,20	0,00	0,00	0,00	0,40
Advertise	0,58	0,00	0,00	0,08	0,08
Airplane	0,61	0,00	0,50	0,05	0,05
Banjo	0,00	0,00	0,00	0,71	0,00
Baseball	0,10	0,02	0,00	0,00	0,86
Guitar	0,00	0,02	0,00	0,83	0,01

Table 8. Most similar 4 terms to some tags using NCDU

	(1)	(2)	(3)	(4)
Architecture	Rio	Skyscraper	Historic	Building
Canada	Quebec	Edmonton	Ontario	Toronto
Art	Actress	Rio	Craft	Fine
Fun	Food	Lifestyle	Teenager	Zoo
Cat	Kitten	Food	Dolphin	Amazon
Band	Music	Ballroom	Gig	Guitarist
Famous	Actress	Food	Interestingness	Celebrity
Car	Nissan	Automotive	Ford	Mustang

Table 9. Most similar 4 terms to some tags using Co-occurrence

	(1)	(2)	(3)	(4)
Architecture	Animal	Flower	Cat	Tree
Canada	Food	Animal	Flower	Cat
Art	Animal	Music	Flower	Tree
Fun	Music	Animal	Friend	Cat
Cat	Animal	Flower	Tree	Dog
Band	Music	Live	Rock	Nightclub
Famous	Food	Yahoo	Interestingness	Brazil
Car	Day	Race	Bahrain	Animal

In this step, we generate also a similarity matrix of our folksonomy based on the NCDU measure. This similarity measure gives more accurate results than CDU, cooccurrence, and cosine. As an example, we give in table 7 an excerpt of the NCDU matrix and in Table 8-10 we give the most similar 4 terms to some tags.

• C.    Preparation of tags

As explained above, context identification and disambiguation are performed in one-step by applying a new clustering algorithm. Fig. 3 and 4 depict examples of ambiguous tags “player”, and “adventure” from Flickr. Fig.3 shows an example of the ambiguous tag “design” as they are detected by the algorithm.

ns 0.6				player
0.5
0.4				■ player
л ч 0.3
Л 3 0.2
Л 1
0.1 0
	О ' о		0.0.0.^ о "° '^ о О с 5 " = | Е 8    £ а - 2

Fig. 3. The ambiguous tag ”player” as detected by the algorithm

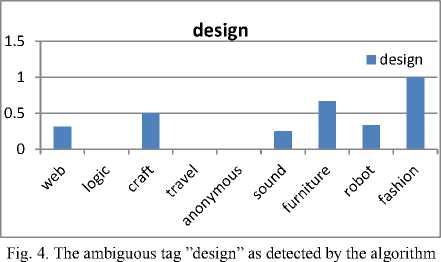
Table 11 shows other examples of ambiguous tags detected by this algorithm.

Table 11. An expert of discovered ambiguous tags with their context

Tags	Cluster centers
Track	Sport / transport

Entertainment	Music/sport
Swing	Music/sport
Speed	Sport/ transport / engine
Music	Mp/ loop/ sound
Spider	Web/ robot
Video	Multiplication/ sound

• D.    Semantic identification

In this step, we have generated hierarchies of tags using the algorithm described in Section 3.4. Fig. 5. and 6., illustrate excerpts of these hierarchies for Flickr and Delicious tags respectively.

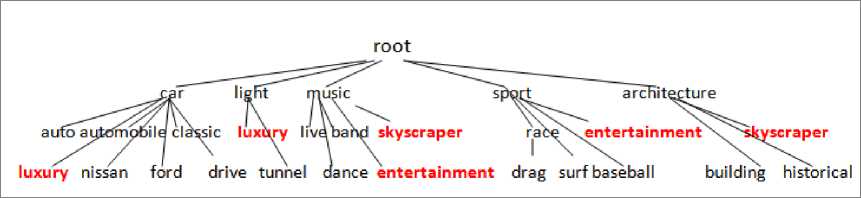
Fig. 5. A small excerpt from the tag hierarchy created for Flickr tags (red tags are ambiguous ones)

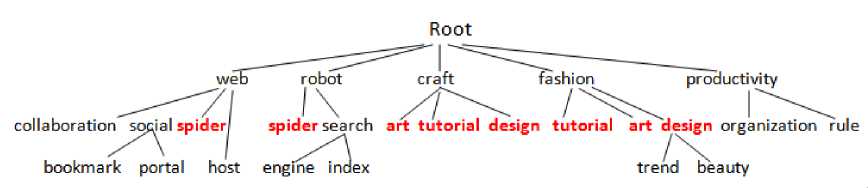
Fig. 6. A small excerpt from the tag hierarchy created for Delicious tags (red tags are ambiguous ones)

• E.    Evaluation

In order to evaluate the quality of the learned hierarchy, we compare it with manually built categorization schemes from WordNet and Wikipedia. Despite that, it is not obvious to find a valid similarity score for two hierarchical structures. For this purpose, we use the measures proposed by [8], namely F-measure and taxonomic overlap measures. The principal is to find a concept present in the two hierarchies and to extract excerpt from both ontologies containing this concept, then the similarity of the two hierarchies depends of the similarity of the two excerpts.

Based on these measures and both ontologies we run several experiments to assess the quality of our approach. For this purpose, we have generated taxonomies based on co-occurrence, cosine, and NCDU measures. The results of the comparison are depicted in Fig. 7 based on taxonomic overlap, and in Fig. 8 based on F-measure.

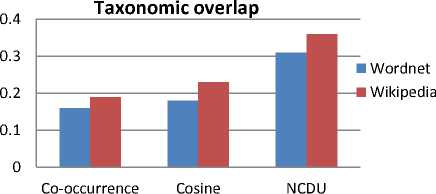
Fig. 7. Taxonomic overlap based comparison between the learned hierarchical structures and the reference ontologies from WordNet and Wikipedia

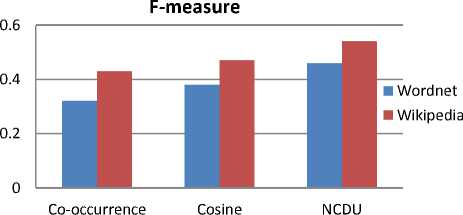
Fig. 8. F-measure based comparison between the learned hierarchical structures and the reference ontologies from WordNet and Wikipedia.

We have also tested the quality of the proposed similarity measure (NCDU). For this reason, we have used Kendall rank correlation coefficient referred to as Kendall's τ coefficient. It is a statistic used to measure the association between two measured datasets.In our experiments, we calculate τ correlations between the similarity values based on co-occurrence, cosine and NCDU measures on one hand and the reference similarity values provided by the WordNet grounding measure on the other hand. The formula of τ is as follows:

(number of concordant pairs) -(number of discordant pairs) τ=-------J--------------

Р (Р-1)

Where P is the total number of pairs, and concordant pairs are defined as follows:

Given two pairs p1= (t 1 ; t 2 ) and p2= (t 3 ; t 4 ). p1 and p2 are concordant if t 1 > t 3 and t 2 > t 4 , or if t 1 < t 3 and t 2 < t 4 . Values of τ ranges from -1 to 1, where -1 means that all the pairs are discordant, and 1 means that all are concordant.

Fig. 9 plots Kendall’s correlation between generated similarities, and the WordNet reference.

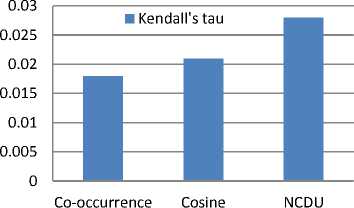
Fig. 9. Experimental results of comparing generated similarities with WordNet reference

We have used the same formula to compare the proposed generality measure FDU with the frequency based generality measure. However, here we have another definition of concordant pairs and discordant ones. Given a pair of tags p= (t 1 ; t 2 ), p is a concordant pair if we have t 1 > t 2 in a generality measure as well as in WordNet.

Fig. 10 illustrates comparison between these generality measures.

The objective of evaluating a fuzzy clustering algorithm is to seek clustering schemes where most of the vectors of the dataset exhibit high degree of membership in one cluster. For this purpose, we have used the partition coefficient (PC) [11] to compare our algorithm to the FCM.

=

1∑∑

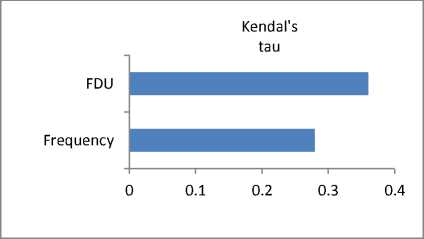
Fig. 10. Experimental results of comparing generality degrees with WordNet reference.

Where n, and k are tags count and clusters count respectively.

We perform a set of experimental results to compare the performance of our new algorithm and the FCM. The experiments are done on a personal computer with Intel core i3 2,4 GHz at 64 bit, 4 GB of memory and 464 GB hard disk. It is obvious that our new algorithm outperforms in a remarkable way the FCM algorithm in term of quality of clusters and in term of performance as shown in Fig. 11 and Table 12.

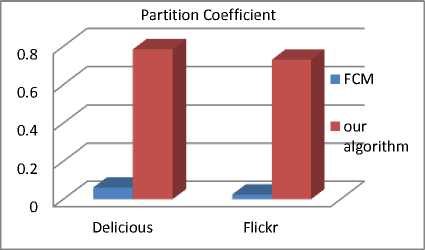
Fig. 11. Experimental results of comparing the quality of our new algorithm and the FCM one based on the partition coefficient PC.

Table 12. Experimental results of comparing the runtime performance of our new algorithm and the FCM.

	Delicious	Flickr
FCM’s runtime in seconds	622,349	593,288
Our algorithm’s runtime in seconds	1,214	1,035

• V.    Conclusion

Folksonomies have their own shared vocabularies and relations, which can be extracted as an ontological structure. In recent years, there has been a growing number of research works trying to associate semantic information to tags in folksonomies. The main objective of these works is to identify the shared conceptualizations hidden in folksonomies.

Although several approaches have been proposed to bring structure to folksonomies, they do not come without limitations. These include the inability to decide the rules generated by association rule mining as to which term is more general or narrow, and tags that cannot be found in the upper ontologies. Moreover, tags disambiguation task and calculus of similarity between tags still suffer from several limitations.

In this paper, we have proposed an integrated approach to extract ontological structures from collaborative tagging systems. We proposed a simple representation of the folksonomy in the vector space model to reduce calculations time. Our approach tries also to overcome the limitations of the other approaches by introducing all levels of a folksonomy in calculating similarity between tags. We propose also anew algorithm to define context of tags and to detect ambiguous ones. Moreover, we ameliorate the approach of Heymannet al [7] by employing the clusters generated in the context identification and disambiguation task, in the hierarchy generation task. The study shows the approach has significant potentials for ontology extraction from folksonomies.

For future work, we will attempt to ameliorate the similarity measure used in this work by combining it with semantic similarity measures like those presented in [33].

Moreover, we plan to improve the approach by discovering non-taxonomic relations by detecting tags representing verbs and their related tags. Finally, we plan to extrinsically assess the quality of our results by integrating them in the context of various tasks such as tag disambiguation, result visualization, and ontology evolution.