Анализ динамики и тенденций изменения ВРП Воронежской области на основе модели авторегрессии первого порядка

Валовой региональный продукт (ВРП) является главным макроэкономическим показателем динамики и уровня развития экономики. Он отражает результат воздействия целого комплекса факторов, среди которых ведущим является объем инвестиций в основной капитал. Поскольку инвестиции являются мультипликатором экономического развития, увеличение объема инвестиций в экономику

Слинькова Н.В. Анализ динамики и тенденций изменения ВРП Воронежской области на основе модели авторегрессии первого порядка // Вестник ВГУИТ. 2018. Т. 80.  № 3. С. 382–385.

прямо пропорционально влияет на объемы валового регионального продукта и в текущем, и в последующих периодах. При этом можно утверждать, что такое влияние является взаимным – увеличение объемов ВРП, в свою очередь, стимулирует приток инвестиций в экономику региона и способствует дальнейшему росту ВРП.

Ввиду высокой степени корреляции между показателями объемов инвестиций и ВРП, а также прямой зависимости между

Vestnik VGUIT [Proceedings of VSUET]. 2018. vol. 80. no. 3.

ними, в некоторых работах [1–3] предлагается использовать модель линейной регрессии для анализа данных показателей. Однако такой подход не дает информации о долгосрочном влиянии инвестиционной деятельности на экономику, не учитывает инерционности, присущей сложной системе экономики государства или региона, а также мультипликативной роди инвестиций.

Вышесказанное позволяет сделать предположение о целесообразности использования авторегрессионной модели для анализа динамики и прогнозирования объемов ВРП. Целью данной работы является изучение возможностей использования авторегрессионных моделей для анализа и прогнозирования состояния экономики региона, а также построение такой модели по данным Воронежской области, оценка адекватности и качества модели.

Теоретический анализ и исходные данные

Включение в эконометрические модели значений результативной переменной в предыдущие моменты времени в качестве факторов возможно с помощью моделей авторегрессии. Модели этого типа описывают случаи, когда влияние причины на следствие является пролонгированным. В общем случае модель авторегрессии можно представить в следующем виде:

y = a + b 0 x t +c 1 y t-1 + … +c n y t-n , (1) где n – порядок модели авторегрессии.

Таким образом, с помощью подобной модели можно учесть инерционность изучаемого явления, когда уровень результативного показателя в текущем периоде в значительной степени зависит от его уровней, достигнутых в предыдущих периодах.

Описанные свойства авторегрессионных моделей во многом соответствуют основополагающим характеристикам динамики валового регионального продукта. Рассмотрим построение модели авторегрессии на примере показателей валового регионального продукта и инвестиций в основной капитал в Воронежской области (таблица 1) [4].

Воронежская область является динамично развивающимся регионом с диверсифицированной экономикой. В течение всего периода с 2000 года в области не наблюдалось снижения ВРП даже в кризисные для экономики РФ годы. Объемы инвестиций в основной капитал также стабильно возрастали в рассматриваемом периоде. Таким образом, можно говорить о высокой устойчивости экономики региона (рисунок 1) .

Таблица 1.

Показатели экономического развития Воронежской области за 2000–2016 гг.

Table 1.

Indicators of economic development of the Voronezh region for 2000-2016

Годы Years	Инвестиции в осн. капитал, млн руб. Investments in fixed assets, mln. rubles	ВРП, млн руб. GRP, mln. rubles
2000	8 262,00	49 523,90
2001	10 409,00	60 014,60
2002	15 964,00	83 001,10
2003	19 756,00	100 143,30
2004	21 845,00	117 197,60
2005	28 652,00	133 586,60
2006	38 867,04	166 176,50
2007	65 319,29	222 811,90
2008	94 168,00	287 072,10
2009	94 788,00	301 729,10
2010	125 825,50	346 568,20
2011	155 244,86	474 973,90
2012	182 334,32	563 965,40
2013	216 983,05	611 720,40
2014	240 272,22	717 667,20
2015	264 659,81	805 969,60
2016	270 992,14	841 375,70
2017	294168,51	–

*На момент написания статьи официальные данные о размере ВРП Воронежской области за 2017 г. отсутствуют

* At the time of writing, official data on the The amount of GRP of the Voronezh region for 2017 are absent

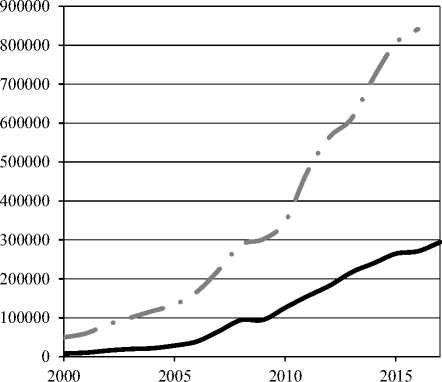
^^^^^^w Инвестиции в основной капитал, млн.руб

^^^^w ♦ Валовой региональный продукт, в текущих ценах, млн.руб

Рисунок 1. Динамика ВРП Воронежской области и объемов инвестиций в основной капитал [4]

Figure 1. Dynamics of GRP of the Voronezh region and the volume of investment in fixed capital

Экспериментальная часть

Можно отметить, что направление динамики ВРП и объема инвестиций в основной капитал в Воронежской области имеет схожие характеристики, коэффициент линейной корреляции для рассматриваемых показателей составляет 0,997. Построим по имеющимся данным двухфакторную авторегрессионную модель первого порядка AR(1), учитывающую влияние инвестиций в основной капитал и значений ВВП в предыдущем периоде. Модель будет иметь вид y t = a + b o x t +c 1 y t -1 +S t , где x t - объем инвестиций в основной капитал, млн руб., y t – ВРП Воронежской области в текущем периоде, млн руб., y t -1 – ВРП Воронежской области в предыдущем периоде, млн руб., S t - случайная (стохастическая) компонента.

Наличие лаговых значений результативного признака в правой части уравнения приводит к нарушению предпосылки МНК о делении переменных на результативную (стохастическую) и факторные (нестохастические) [5, с. 325]. Кроме того, существует корреляционная зависимость между лаговыми переменными и ошибкой [6, с. 191]. Присутствие таких свойств у авторегрессионных моделей делает невозможным получение несмещенных, эффективных и состоятельных оценок параметров модели с помощью обычного МНК. Одним из способов преодоления данной проблемы является использование инструментальных переменных [7, с. 212]. Такие переменные должны в значительной степени коррелировать с исходными переменными, но не должны иметь корреляционной связи с ошибкой модели. В качестве инструментальной переменной возьмем переменную y t -1 , определяемую соотношением y t -1 = d o +d i x t -1 , в котором коэффициенты d 0 и d 1 получены с помощью обычного МНК. Получим уравнение инструментальной пере-менной y_t -1 = 38737,9 + 2,793 x t -1 .

В [5, с 327] отмечена проблема мультиколлинеарности факторов y t -1 и x t , которая возникает вследствие функциональной зависимости между y t -1 и x t -1 . В тех же источниках предлагается для снижения негативного влияния мультиколлинеарности на оценки параметров включать в модель фактор времени в качестве независимой переменной ( t ). Поэтому далее будут рассмотрены два вида уравнения авторегрессии y t = a + b o x t +c 1 y t -1 +S t и y t = a + b o x t +c 1 y t -1 + с 2 t + S t .

При оценке параметров уравнения y t = a + b o x t +c 1 y t -1 +S t с ненулевой константой a выявлено, что значимость данной константы ниже заданного уровня значимости в 5%. Экономический смысл данного параметра также неочевиден, поэтому построена модель 384

с нулевым свободным членом. МНК получено следующее уравнение:

y t = 0,917x t + 0,597y t-i +8111,334 t.   (2)

Полученная модель имеет высокие показатели значимости и адекватности: коэффициент детерминации R ² равен 0,9986 (нормированный R ² = 0,92), F-статистика Фишера составляет 3168,9 (табличное значение 3,49), средняя ошибка аппроксимации 5,8%. Все коэффициенты при факторных признаках модели также являются значимыми на уровне 5%. Однако проверка модели на автокорреляцию в остатках, проведенная с помощью критерия h Дарбина показала, что гипотеза об отсутствии автокорреляции отклоняется, поскольку h = 4,95, и нарушается условие t a/2 < h < 1 1 -0/2 , где t_o /2 = -1,96, 1 1 - a/ 2 = 1,96 -квантили распределения Стьюдента порядка a/2,1-a/2 . Таким образом, оценки параметров данной модели не могут считаться несмещенными, т. к. нарушено одно из условий теоремы Гаусса-Маркова.

Найдем МНК оценки параметров уравнения авторегрессии без учета фактора времени, получим:

y t = 29512,23 + 1,579 x t + 0,485 ŷ t-1 .   (3)

Полученная модель также имеет высокие показатели значимости и адекватности: коэффициент детерминации равен 0,996, F-статистика Фишера составляет 1811,14 (табличное значение 3,49), средняя ошибка аппроксимации 6%. Все коэффициенты при факторных признаках модели являются значимыми на уровне 5%. Критерий h Дарбина для данного уравнения составляет 1,36, условие t a/2 < h < 1 1 -a/2 , при t a/ 2 = -1,96, t 1 - a/ 2 = 1,96 выполняется. Таким образом, гипотеза об отсутствии автокорреляции в остатках принимается.

Для прогноза значений ВРП и интерпретации полученных оценок параметров будем использовать модель авторегрессии без учета фактора времени. Используя данные об объеме инвестиций в основной капитал в 2017 г., можно рассчитать прогнозное значение ВРП. Оно составит 902306,9 млн руб. Определим границы возможных значений ВРП по формуле:

^{y ˆ}0 ^{± t} 1 - α ; n - k - 1 ^{⋅ s}y ˆ 0                (4)

где   y ˆ ₀   – расчетное значение прогноза;

t1-α;n-k -1 – значение t-критерия Стьюдента на уровне значимости a при числе степеней свободы n-k-1 (n – число наблюдений, k – число параметров модели);  syˆ   – выборочная среднеквадратическая ошибка, рассчитанная по формуле:

Sy = Socm • 41 + XT0(XTX)-1 X0    (5)

где s ост – остаточная сумма квадратов отклонений.

При заданном уровне значимости (α = 0,05) значение ВРП за 2017 г. будет находиться в пределах от 854559,52 млн руб. до 950054,27 млн руб.

Важным свойством полученной модели является возможность оценки масштабов влияния инвестиций в основной капитал на динамику ВРП в краткосрочной и долгосрочной перспективе [8]. Увеличение инвестиций на 1 млн руб. приводит к росту ВРП в текущем периоде в среднем на 1,58 млн руб. и на 3,07 млн руб. в долгосрочной перспективе.