Анализ эффективности дискретных покрытий рабочих органов при очистке растительного сырья

DOI:

Анализ состояния развития очистительного оборудования для растительного сырья, картофеля, моркови, лука и других видов овощей и корнеплодов свидетельствует о том, что значительная часть его использует в качестве рабочих органов абразивные вкладыши, усовершенствование которых является одним из эффективных методов улучшения его эксплуатационных характеристик.

Механический способ очистки, реализованный на рассматриваемом типе машин, позволяет получать полуфабрикат с высокими потребительскими свойствами, создавать машины небольшой производительности, пригодные для использования как на предприятиях пищевой промышленности, так и в общественном питании. Все это свидетельствует о необходимости исследования возможностей совершенствования абразивных покрытий рабочих органов очистительных машин [1].

Удаление с клубней наружных покровов происходит в рабочих камерах овощечисток периодического действия острыми гранями абразивных зерен. Клубень, попадая на абразивную поверхность, приводится по отношению к ней в относительное движение. В момент соприкосновения с абразивной поверхностью клубень трется об нее, в результате чего между ними возникает сила трения, направленная в противоположную инерционной силе сторону. Одновременно происходит закручивание клубня и степень изменения скорости и направления движения клубня в результате соприкосновения его с абразивной поверхностью в значительной мере зависят от взаиморасположения соседних клубней и участка соприкосновения поверхности клубня с абразивной поверхностью. Осуществим более детальное рассмотрение процесса очистки с помощью моделирования.

Моделирование и численный эксперимент

Рассмотрим классическую модель движения клубня в камере очистительной машины [2]. Она предполагает следующие допущения: клубень рассматривается как правильная сфера, перемещение которой происходит под действием центробежной силы, силы трения и силы собственной тяжести клубня без учета влияния остальных клубней, находящихся в рабочей камере. Как показывает многолетний опыт использования рассматриваемого оборудования, подобная модель позволяет достаточно точно определить кинематику движения клубня по рабочей камере, в том числе и рассчитать угол, под которым основная масса клубней попадает на рабочую абразивную поверхность.

При попадании на плоскую часть абразивной чаши клубень начинает вращаться с ней, но с меньшей скоростью. Между диском и клубнем наблюдается проскальзывание, которое можно учесть коэффициентом проскальзывания, равным:

_{l =} ω _р - ω _к

ω р

где ω _к – угловая скорость клубня картофеля;

ω _р – угловая скорость рабочего органа.

Тогда скорость продукта относительно днища будет равна:

ω к ¹ = l ω р                 (2)

Коэффициент проскальзывания, как правило, принимают равным 0,2.

С учетом этого замечания на первом участке, плоском диске чаши, это условие в соответствии с описанным выше характером перемещения клубней запишется в виде:

C≥T или m⋅4π2⋅n2⋅l2⋅r≥f⋅m⋅g,         (3)

где n – частота вращения чаши, об/сек; f – коэффициент трения (принимается в пределах от 0,8 до 1,3); m – масса клубня; r – переменный радиус вращения клубня.

На втором участке, конусном, на клубень картофеля действуют те же силы C – центробежная, Т – сила трения и G – вес клубня. Под действием этих сил клубень должен быть выброшен к стенке. При составлении уравнения сил, действующих на клубень, появляется такой конструкционный параметр, как угол при вершине конуса Θ.

Раскладывая эти силы на две составляющие: перпендикулярно наклонной стенки чаши С_N и G_N , а также направленные вдоль этой поверхности C_O и G_O можно записать

C_O = C ⋅ sin θ ; C_N = C ⋅ cos θ ; G_O = G ⋅ cos θ ; G_N = G ⋅ sin θ .

Спроецируем силы, действующие на клубень, на оси O и N. Проекции силы тяжести и центробежной силы на ось N будут уравновешиваться силой реакции N со стороны наклонной стенки:

N = C N + G N            (4)

Под действием силы реакции N возникает сила трения, направленная в сторону, противоположную скорости движения клубня относительно диска:

T = f • ( C n + G n )             (5)

Условие движения клубня на этом участке определяется уравнением:

C o >  G o + T             (6)

Для условий движения клубня картофеля на участке поверхности конуса необходимо, чтобы составляющая силы инерции, действующая вдоль конусной поверхности, превосходила суммарное воздействие от сил трения и скатывающей силы.

Это можно записать следующим образом в преобразованном виде:

m m p (1 - 1 ) 2 r sin 0> mg (cos 0 + f ),   (7)

где r – расстояние от оси вращения чаши до центра клубня, g – ускорение свободного падения.

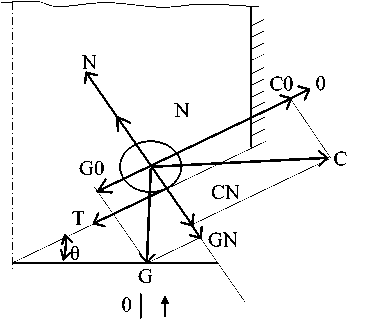
Рисунок 1. Схема силового взаимодействия клубня картофеля с конической частью абразивной чаши

Figure 1. Scheme of the power interaction of the potatoes tubers with cone-shaped part of abrasive chalice

Принимая в данном процессе т к = 38 рад/с, r = 0,1 м, l = 0,6, получают значение для угла подъема Θ = 0,34 рад. При производстве абразивных чаш с запасом берут угол при вершине конуса, равный 30 градусам.

Для оптимизации процесса очистки необходимо установить траекторию движения и рассчитать угол вылета клубня с конической чаши. Рассмотрим отдельно взятый клубень картофеля. Предполагая его однородной сферой и не учитывая влияние на него других клубней, определим траекторию его движения по конической чаше и угол, под которым клубень вылетит к стенке. Угол наклона конусной чаши к горизонту примем 30 градусов.

На находящийся на конической чаше клубень, действуют следующие силы: сила тяжести G = mg, направленная вертикально вниз, центробежная сила C = mm2 (1 -1 )2 r, стремящаяся отбросить клубень на цилиндрическую стенку, и сила трения, направленная противоположно вектору скорости [3]. Для расчетов примем следующие значения величин:

m = 0,2 кг - масса одного клубня; g = 9,81 м/с²

• - ускорение свободного падения; т = 40 рад/с, угловая скорость вращения конической чаши;

• 1    = 0,4   - коэффициент проскальзывания

клубня по чаше; r , м – переменный радиус вращения клубня, изменяется от 0 до 0,25 м.

Под действием этих сил клубень совершает составное движение (рисунок 2). Переносное движение будет вращательным вокруг оси Z с переменной скоростью тк = т(1 -1) = 24 рад/с, относительное движение будет прямолинейным. Тогда в любой момент времени переносная скорость ue = ткt будет направлена перпендикулярно к плоскости треугольника OMZ, а отно-dl сительная скорость — = — будет направлена r dt вдоль прямой 1 = OM .

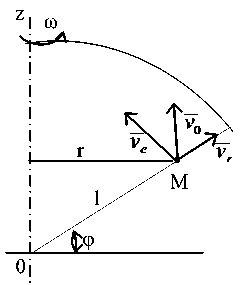
Рисунок 2. Схема векторов скоростей клубня

Figure 2. Scheme of vector of tubers velocities

По теореме сложения скоростей найдем, что вектор абсолютной скорости и_а = ue + u _r , а угол его наклона к горизонту будет искомым углом подъема спирали 0( t ).

Из треугольника скоростей нам известно ctg(0) = —-. Рассмотрим изменение скоростей

Ur и угла подъема спирали, происходящее за пренебрежимо малое время dt. Учтем, что расстояние от вершины конуса до места нахождения клубня 1 = OM связано с переменным радиусом враще-

30 ^

ния r следующей зависимостью: r = 1 cos( ^^).

3               dl

Тогда А — = m 1 , а. А — = — e К 2              r dt

.

Из треугольника скоростей определим соотношение: ctg(0) = ^e-^-AU

.

В таком случае приращение угла подъема за пренебрежимо малый промежуток времени составит: A0 = arcctg ^e = arcctg (— ю_к t ) (7)

A u r           2 К

Проинтегрируем выражение по времени t:

0 = tarcctg (20,76 1 ) + 2,41 - 10 - 2 ln(1 + 431 t ²) (8)

В левой части мы получим значение угла 0, а в правой его зависимость от времени. Нам останется только определить, какое время проведет клубень на конической чаше [4].

Рассмотрим, на что расходуется подаваемая от электродвигателя энергия (его мощность N Э = 0,75 кВт ). С учетом потерь в соединительных муфтах ( п м = 0,99 ) и ременной передаче п рем = 0,97 на вал конической чаши подается следующая мощность: N к = N Л . Ч™ = 0,75 - 0,99 2 - 0,97 = 0,71кВт.

Она будет расходоваться на сообщение кинетической и потенциальной энергии клубням, находящимся на конической чаше. Их количество примем равным 25 % от всей массы загруженных клубней, то есть суммарная масса единовременно находящихся на конической чаше клубней будет равна M = 5,5 кг.

Получим уравнение энергетического баланса, из которого можно выделить требуемое время t . При составлении уравнения коэффициент α будет учитывать потери на трение, а коэффициент β – взаимодействие клубней между собой. Оба коэффициента зависят от модуля упругости картофеля и, соответственно, от срока его хранения. Причем значение α будет возрастать, а значение β будет уменьшаться при хранении с уменьшением модуля упругости. Но их произведение при этом меняться будет незначительно и может быть принято при расчетах значению 0,65. Уравнение будем решать в системе Mathcad [5].

N K = „Р (Mg*^ + M («^ cos ^{0 1} ) (9)

Корнем этого уравнения является значение времени t = 0,07с, которому соответствует угол 0 = 35 градусов.

Проанализируем полученную формулу и попытаемся определить, насколько существенными будут изменения значений t при варьировании следующих величин: l и ю _к . Учтем при

Ю р ^{- Ю} .

этом, что l =— ---- и, следовательно:

^ю р

^Ю к = Ю р ( 1 - ¹ )               (10)

Сама же величина коэффициента проскальзывания изменяется от 0,3 до 0,45. Рассчитаем соответствующий угол Θ для трех значений коэффициента проскальзывания (0,3; 0,4; 0,45) с помощью указанной выше формулы в системе Mathcad. Полученные результаты сведем в таблицу 1

Таблица 1

Результаты численного эксперимента

Table 1

The results of the numerical experiment

Коэффициент проскальзывания, l	Скорость вращения клубня Ю к , рад/с	Время контакта t , c	Угол вылета Θ, градусы
0,35	26	0,05	29,1
0,4	24	0,07	31,6
0,45	22	0,08	33,8

Проанализировав полученные данные, можно сделать вывод о несущественном изменении угла вылета клубней с конической части чаши и о допустимости принятия значения этого угла, равного 30 градусам, для дальнейшего рассмотрения и проведения исследований.

Эти результаты позволяют оптимизировать рисунок нанесение абразивных полос, если принять за метод усовершенствования процесса очистки прерывистое нанесение покрытия. Во многих отраслях успешно внедряется, так называемый, многолезвийный режущий инструмент, изготавливаемый методами гальваностегии, путем закрепления металлической связкой на металлической подложке высокопрочных абразивных зерен. Такой инструмент, воздействуя на обрабатываемый объект одновременно многими режущими кромками, прочно закрепленными на подложке, имеет большую долговечность и обеспечивает “мягкий” режим поверхностного слоя материала Преимущество такого покрытия состоит в том, что контакт очищаемого объекта с рабочим органом периодически прерывается, следовательно, исключается тепловое насыщение поверхностных слоев обрабатываемого материала. Такой подход позволяет повысить качество очистки при одновременном увеличении производительности, сократить энергозатраты, увеличить время работы абразивов без засаливания, улучшить качество очистки сырья, а также снизить количество отходов.

Одной из возможностей улучшения качества очистки картофеля в камерах конусных картофелеочистительных машин является замена боковых вставок из сплошного абразива на вставки с прерывистым нанесением абразива (рисунок 2).

Такие покрытия рабочих органов состоят из пластмассовой подложки 1 с закрепленными на ней полосами терочных элементов 2, которые имеют дополнительный слой 3 из электропроводного материала (медной фольги). Торцы слоя 3 закрыты металлической связкой. При приведении рабочих органов в движение корнеплоды начинают перемещаться относительно покрытия и прижиматься под действием силы тяжести и центробежной силы к терочным элементам, которые надежно удерживаются на подложке посредством слоя 3. Остро выступающими гранями абразивных частиц терочные элементы 2 снимают с корнеплодов тонкий слой кожуры. Проходя последовательно все абразивные полосы одну за другой, клубни очищаются от кожуры. При этом, проходя каждую очередную полосу терочных элементов 2, они выталкивают из зазоров между отдельными абразивными частицами кожуру от предыдущего клубня в межполосовое пространство. Откуда кожура смывается струями воды.

Конструкционными параметрами таких рабочих органов являются ширина полос a, расстояние между полосами b и их угол наклона ά.

При малых зазорах между терочными элементами в них накапливается счищаемая с картофеля мезга, которая забивает их, приводя к традиционному “засаливанию”. Особенно сильно это влияет на рабочие органы с малой зернистостью. Чрезмерное увеличение зазоров, а, следовательно, и отношения a , приводит к тому, b что наиболее эффективно работают только кромки терочных элементов, которые воздействуя на клубень ударом, по-видимому, отдаляют его от терочной поверхности и не дают ей полностью реализовать свои абразивные способности.

Угол наклона полос ά определяется, исходя из того, что наиболее эффективно процесс очистки идет при движении клубня перпендикулярно абразивным полосам. При таком взаимном расположении будет минимальна величина поперечного закручивания клубня и отклонение его траектории от винтовой, а выталкивание частиц кожуры в межполосное пространство будет идти наиболее активно, что поспособствует уменьшению вероятности засаливания абразива. При прерывистом нанесении абразива очистка идет не только за счет микротрения, но и, как при токарной обработке резцом, за счет процесса резания острой кромкой абразивной полосы (рисунок 3). Пластины с прерывистым нанесением абразиваПоскольку угол наклона абразивных полос определяется по формуле:

ά = 90-Θ,               (11)

для изготовления рабочего покрытия остается только подобрать ширину абразивных полос.

Рассмотренная выше модель движения не учитывала взаимодействие отдельных элементов очищаемого сырья между собой. Такой подход был оправдан при кинематическом расчете угла вылета клубня с конической части абразивной чаши, но не подходит для этапа перемещения картофеля вдоль неподвижной цилиндрической стенки.

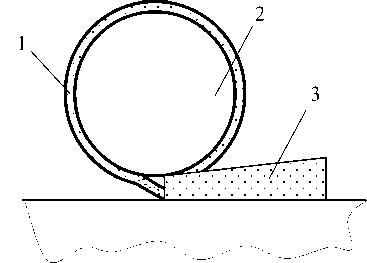
Рисунок 3. Схема воздействия кромки абразивной полосы на клубень

Figure 3. Scheme of the influence of the edge of the abrasive band on tuber

Предполагая отдельные очищаемые элементы (например, клубни картофеля) упругими элементами, заменим их (в плоской постановке) жесткими дисками, соединенными между собой упругими пружинами. Предположим дополнительно крайний левый клубень закрепленным неподвижно (опертым на основную массу очищаемого картофеля). Взаимодействие трех контактирующих между собой и со стенкой рабочей камеры клубней можно тогда рассматривать в рамках следующей задачи: определить частоты свободных колебаний и найти формы главных колебаний системы с двумя степенями свободы, указанной на рисунке ( l 01 и l 02 – длины недеформированных пружин 1 и 2). Система состоит из двух однородных дисков, присоединенных к вертикальным поверхностям пружинами с коэффициентами жесткости с 1 и с 2 и соединенных пружиной с коэффициентом жесткости с 3 .В состоянии покоя пружины с коэффициентами жесткости с 1 и с 2 растянуты соответственно на величины f ст1 ; f ст2 . Пружина с коэффициентом жесткости с 3 сжата на величину f ст1 + f ст2 .

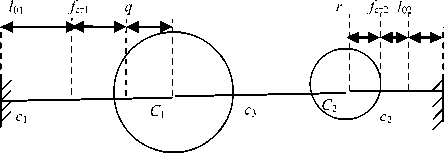
Рисунок 4. Модель взаимодействия клубней Figure 4. Model of the tubers interaction

За обобщенные координаты примем: q, r – горизонтальные смещения центров масс дисков 1 и 2 от положения статического равновесия. На рисунке показано положение системы при положительных обобщенных координатах.

Найдем кинетическую и потенциальную энергии системы. Кинетическая энергия системы состоит из кинетической энергии дисков:

т = т + т = сс + -Icl + сс + J 2 ^ 2 (₁₂)

12 2222,

или

Таким образом,

Т = -^( m ₁ q ² + m ₂ r ²),

П = 1/ 2 с ₁ q ² + 1/ 2 с ₂ r ² +1/2 с ₃ ( q + r ) ²

Т = 1/ 2( а₁₁ + 2 а ₁₂ + а ₂₂);

П = 1 / 2( с ₁₁ q ² + 2 с ₁₂ qr + с ₂₂ r ²).

где q , r - обобщенные скорости; J 1 , J 2 - моменты инерции дисков относительно осей, проходящих соответственно через их центры масс С 1 и С 2 . Моменты инерции дисков будут:

mr ²

J = -r- , i = 1,2          (13)

Здесь а ij – коэффициенты инерции: а 11 = 3 3

т1, а12 = 0, а22 = т2; cij – коэффициенты жесткости: с11 = с1+с3, с12 = с3, с22 = с2+с3.

Для рассматриваемой консервативной системы уравнения Лагранжа имеют вид

q т.к. ®1 = — , r1

r to2 = — r1

то

Т = -(

• 2 .         -2

T i q + m 2 г*

) .

d ( д T ) д T _ дП d (д T ) д T _ дП

—— —  — ^^^^—   — —    --—--

;.

dt ^5 <7 ) д q     д q dt V д i" ) д r     д r

Вычислив производные

Потенциальная энергия системы равна работе сил при перемещении системы из отклоненного положения в нулевое (положение статического равновесия). Потенциальную энергию системы вычислим как потенциальную энергию деформированных пружин. Деформации пружин следующие: λ 1 = q + f ст1 – для пружины с коэффициентом жесткости с 1 , λ 2 = r + f ст2 – для пружины с коэффициентом жесткости с 2 ; λ 3 = q + r + f ст1 + f ст2 – для пружины с коэффициентом жесткости с 3 . Следовательно,

П = 1/2 C 1 (q + f_cm 1 )² - 1/2 с + 1/2 с ₂( r + f_{cm 2})² -- 1/2 с 2 + 1/2 с 3 ( q + r + f em 1 + f em ₂) 2 - 1 / 2 с 3 ( f em 1 + f m 2 ) 2

I T = 0

д q дП

— = сц q + с12 r дх1

I T = 0- д r дП

д T

— = ан q, д <7

d ( д T )

—I — I = а,, q dt V д <7 )        -

,

д T

— = о, r , 22

д r

----= с ₂₁ q + с ₂₂ r . дx ₂

d (I t ^ dt V д r^- )

= а ₂₂ r

и подставив их в уравнения Лагранжа, получим

а₁₁ q = - с₁₁ q - с ₁₂ r - а₂₂r = - с ₂₁ q - с ₂₂ r , (18)

или после упрощений

П = 1 / 2 с ₁ q ² + 1/2 с ₂ r ² + 1 / 2 с ₃( q + r )² +

⁺ с 1 Cm 1 ⁺ с 2 f m 2 ⁺ с 3 ⁽ 4 ⁺ r ) ⁽ / ст 1 ⁺ / ст 2 ).

Из условий покоя рассматриваемой системы, находящейся под действием сил, имеющих потенциал, имеем:

где с 21 = ^с 12 .

Таким образом, для данной системы дифференциальные уравнения свободных колебаний имеют вид:

а₁₁ q + с₁₁ q + с ₁₂ r = 0, а ₂₂ r + с ₂₁ q + с ₂₂ r = 0. (19)

Частное решение этих уравнений:

q = Asin ( kt + в ), r = Bsin ( kt + в ),   (20)

дП д q

q = 0 r = 0

^с 1 j ™ 1 ^{+ с} 3⁽ j ™ 1

+ / ст 2 ) = 0,

q = 0 r = 0

= ,+cAf , + f a = o. 2 ст 2 3 ст 1 ст 2        .

Потенциальная энергия системы с учетом условий покоя имеет вид:

П = 1 /2 с ₁ q ² + 1/2 с ₂ r ² + 1/2 с ₃( q + r )². (16)

где A и B – амплитуды главных колебаний; k – частоты свободных колебаний; β – начальная фаза колебаний.

Уравнение частот, вытекающее из данной системы дифференциальных уравнений, имеет вид:

( с 11 - а 11 k ²) ( с 22 - а 22 k ²) – c ₁²₂= 0. (21)

Корни этого биквадратного уравнения, соответствующие квадратам частот, определим по формулам:

2     a 11 c 22

k l,2 =

+ a 22 c ll ⁺ V ⁽ a ll c 22 ⁺ a 22 c ll )    ⁴ a ll a 22 ⁽ c 11 c 22    c ll )

2 a ₁₁ a ₂₂

.

Пусть в рассматриваемой задаче: массы однородных дисков т 1 = 0,18 кг, т 2 = 0,18 кг, коэффициенты жесткости пружин: с 1 = с 2 = с 3 = 135 Н/м, тогда а 11 = (3/2) т 1 = 0,27 кг; с 11 = с 1 + с 3 = 270Н/м; с 12 = с 3 = 135Н/м; а 22 = (3/2) т 2 = 0,36 кг; с 22 = с 2 + с 3 = 270 Н/м. Следовательно, частоты свободных колебаний k 1 = 500с^-1; k 2 = 1500 с^-1.

Коэффициенты распределения, соответствующие частотам k 1 и k 2 , в общем случае имеют вид

B 1

A 1

^C ll    аИ^k l

Cl2 - al2kl cl2 al2 kl с22 - а22к'

B д 2 =— = A 2	c ll	a ll k 2	C l2	a l2 k 2	(22)
	с 12	a l2 k 2	с 22	a 22 k 2

В данном случае ^ = - 0,43; ц 2 = 3,46. Уравнения, определяющие первое главное колебание, примут следующий вид:

ql = Al sin (5001 + Pl),(23)

Г = -0,43 A sin (5001 + Д).(24)

Уравнения, определяющие второе главное колебание:

q 2 = A2 sin (l5001 + в2),(25)

r2 = 3,46 A2 sin (l5001 + в2 )•(26)

Общее решение дифференциальных уравнений представляет собой сумму частных решений:

q=q 1 +q 2 = A 1 sin( 500t+β 1 )+ A 2 sin(500 t+β 2 ), (27)

r = r 1 + r 2 = 0,43 A 1 sin( 1500t+β 1 ) +

+3,46 A 2 sin(1500 t + β 2 )        (28)

Значения A i и β i определяются по начальным условиям задачи.

Полученные решения позволяют усовершенствовать конструкцию рабочей камеры, размещая абразивные элементы в тех зонах цилиндрической обечайки, где клубень, контактирующий со стенкой камеры, наиболее интенсивно прижимается к рабочей поверхности. Эти зоны определяются с учетом скорости вращения клубня картофеля и собственной частоты колебаний рассмотренной системы из трех прилежащих к рабочей поверхности клубней.

В общем случае на геометрию расположения абразивных полос должны влиять упругие характеристики пружин – модули упругости мякоти картофеля. Следовательно, учет сезонных изменений структурно-механических свойств картофеля требует применения различных рабочих органов при очистке свежесобранного картофеля и картофеля, прошедшего определенный срок хранения. Кроме того, на частоту колебаний и, соответственно, на требуемую ширину абразивных полос будет влиять масса очищаемых клубней.

Проведем численное моделирование, применяя систему Mathcad. Рассмотрим для этого следующий интервал изменений массы клубней и коэффициента жесткости картофеля. Массу примем изменяющейся от т 1 = 0,18 кг до т 1 = 0,27 кг, а коэффициент жесткости – от с 1 = 135 Н/м до с 1 =160 Н/м (причем при хранении жесткость уменьшается). Построим графики зависимости частот k 1 и k 2 от массы клубня и его жесткости.

Как выяснено ранее, к геометрическим параметрам рабочих органов относятся ширина абразивных полос и расстояние между ними. Для их расчета зададим следующие величины: ώ = 9,6 (рад/ с) – угловая скорость вращения клубня относительно стенок рабочей камеры, d = 0.48 (м) – диаметр рабочей камеры, l = d • π (м) – длина окружности рабочей камеры. Найдем ширину нанесения абразивных полос b(i):

b(i):= o- (29) k ₂( i )

Выводы

Проведенный обзор литературы и анализ практического опыта свидетельствуют о том, что применяемые в настоящее время сплошные абразивные вкладыши на основе зерна карбида кремния и органических связок не могут обеспечить выполнение поставленных условий ресурсосбережения при необходимом качестве получения полуфабриката – очищенных овощей. Более того, они не отвечают современным требованиям по надежности. Настоящими исследованиями выяснено, что для решения указанных проблем целесообразно применение абразивных покрытий с заранее прогнозируемой топологией нанесения абразивного зерна Она, в частности, определяется частотой собственных колебаний очищаемого продукта, обуславливающей ширину наносимых абразивных полос. Для картофеля с учетом возможных колебаний массы клубней и сезонных изменений упругих свойств картофеля эта величина будет колебаться в пределах: от 8,14 мм (при массе 0,18 кг и жесткости 135Н/м) до 9,69 мм (при массе 0,27 кг и жесткости 160 Н/м).