Анализ эффектов ориентации сетки при решении задач многофазной фильтрации с использованием метода конечных элементов
Автор: Гриф А.М.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Технические науки
Статья в выпуске: 12-2 (75), 2022 года.
Бесплатный доступ
Рассматривается влияние эффекта ориентации конечноэлементной сетки при решении задач многофазной фильтрации с использованием специальной математической модели, основанной на использовании метода конечных элементов, явном расчете поля давления и специальной вычислительной схеме для расчета насыщенностей. Проведен вычислительный эксперимент на модели реального месторождения высоковязкой нефти Республики Татарстан, состоящего из нескольких пластов и нескольких десятков действующих скважин. Полученные результаты показывают, что описанная схема моделирования процесса фильтрации с использованием метода конечных элементов не подвержена влиянию ориентации конечноэлементной сетки.
Многофазная фильтрация, моделирование, нефтяное месторождение, метод конечных элементов, конечно-элементная сетка
Короткий адрес: https://sciup.org/170196970
IDR: 170196970 | DOI: 10.24412/2500-1000-2022-12-2-109-114
Текст научной статьи Анализ эффектов ориентации сетки при решении задач многофазной фильтрации с использованием метода конечных элементов
Создание высокоадекватных моделей нефтяных месторождений является основополагающим фактором эффективной разработки и оптимизации технологий нефтедобычи [1, 2]. Широко применяемые для решения задач многофазной фильтрации методы конечных объемов и конечных разностей обладают существенными недостатками, связанными с ограниченной геометрической гибкостью и низкой точностью моделирования разноконтрастных сред [3, 4]. Существенной проблемой при их применении является эффект ориентации сетки - решения, полученные при раз личных поворотах сетки вокруг оси Oz, имеют крайне большие различия, которые могут быть компенсированы лишь повышением порядка элементов. В последнее время для решения задач фильтрации получило распространение применение метода конечных элементов [5, 6], и было необходимо проанализировать, насколько его использование позволяет снижать значимость ориентации сетки.
Математическая модель. Моделирование процесса фильтрации осуществляется с помощью решения уравнений [7, 8].
-div(ри") = "|(ФР"5-), " = 1,M, U" =-K Km grad (P + P"), m = 1M,
где и" - фазовая скорость фильтрации с насыщенностью Sm , фазовой проницаемостью к", вязкостью р и плотностью mm р ; P и P - давление в коллекторе и капиллярное давление фазы; К и Ф - аб- солютная проницаемость и пористость порового пространства.
В случае моделирования несжимаю-щейся смеси, система (1)-(2) становится эквивалентной краевой задаче с условиями на границе
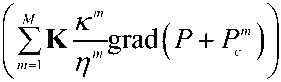
M. K mm d P
m = 1
n m d n
Г2
= 0,
где Г j - проницаемые границы расчетной области Q , через которых в месторождение может поступать нефть/вода, а Г2 - верхняя и нижняя границы расчетной области и элементы перфораций в скважинах.
Для решения краевой задачи (3)-(4) используется метод конечных элементов. В этом случае область моделирования Q представляется в виде объединения конечных элементов Q, а давление представляется в виде непрерывной функции P = 2 p^., коэффициенты разложения j которой могут быть найдены в результате решения СЛАУ
Ap = b .
Здесь вектор p составлен из искомых коэффициентов, а элементы матрицы A и вектора правой части b задаются с помощью соотношений
M К
m
A = JI К2—gradv, • gradVidn,
1=1n )
Q V m--
Mm b, = J OvidQ-J К2—gradP
Г2 Q ^ m = 1 n
• gradv dQ.
По распределению давления можно рассчитать скорость фильтрации смеси
u
1 i
к
-K 2—grad 2 PjVj+ Pm m=1 П V j )
и значения мгновенных объемов, перетекающих через грани смеси
Qy =J uT • nd Г. (6)
i Г i i 1
В этом случае мгновенные объемы отдельных фаз можно найти с использованием соотношения
m
Г i ,Q e
m
"Г i , Q e M П /
Список литературы Анализ эффектов ориентации сетки при решении задач многофазной фильтрации с использованием метода конечных элементов
- Aziz K. S.A. Petroleum Reservoir Simulation // Applied Science Publ. Ltd., London, UK. 1979.
- Shirangi M.G., Durlofsky L.J. Closed-loop field development under uncertainty by use of optimization with sample validation // SPE Journal. Society of Petroleum Engineers, 2015. Vol. 20, № 5. P. 908-922.
- Doyle B., Riviere B., Sekachev M. A multinumerics scheme for incompressible two-phase flow // Computer Methods in Applied Mechanics and Engineering. Elsevier B.V. 2020. Vol. 370. P. 113213.
- Jo G., Kwak D.Y. An IMPES scheme for a two-phase flow in heterogeneous porous media using a structured grid // Computer Methods in Applied Mechanics and Engineering. Elsevier B.V. 2017. Vol. 317. P. 684-701.
- Jackson M.D., Gomes J.L.M.A., Mostaghimi P., et al. Reservoir modeling for flow simulation using surfaces, adaptive unstructured meshes and control-volume-finite-element methods // Society of Petroleum Engineers - SPE Reservoir Simulation Symposium 2013. Society of Petroleum Engineers. 2013. Vol. 2. P. 774-792.
- Abd A.S., Abushaikha A. Velocity dependent up-winding scheme for node control volume finite element method for fluid flow in porous media // Scientific Reports. Nature Research, 2020. Vol. 10, № 1. P. 1-13.
- Numerical modeling of multi-phase flow for various junctions of water and oil saturated layers in 3-D porous media / M.G. Persova, Y.G. Soloveichik, I.I. Patrushev, A.M. Grif // Actual problems of electronic instrument engineering, Novosibirsk, 2-6 Oct. 2018. Vol. 1, № 4. P. 212-215.
- Ovchinnikova A.S., Patrushev I.I., Grif A.M. Modeling of Gas-liquid Mixture Flow Considering the Processes of Gas Liberation and Dissolution // Actual problems of electronic instrument engineering (APEIE-2021): proc. of the 15 intern. sci. and techn. conf., Novosibirsk, 19-21 Nov. 2021. - Novosibirsk: Publ. NSTU, 2021. P. 568-572.
- Persova M.G., Soloveichik Y.G., Vagin D.V., et al. The design of high-viscosity oil reservoir model based on the inverse problem solution // Journal of Petroleum Science and Engineering. Elsevier B.V. 2021. Vol. 199. P. 108245.


