В работе [1] даны постановка и метод решения нелинейной задачи диффузии и испарения эмиссионно-легирующих элементов (активаторов) твердотельных катодов генераторов низкотемпературной плазмы. Ранее [2] решена теплофизическая задача для электродных узлов цилиндрической геометрии катодов данного класса. В сильноточных плазменных системах (СПС), функционирующих в экстремальных условиях по уровням температур на рабочих токах до 15кА, наиболее работоспособными являются составные катодные узлы из сопряженных элементов: «катод (активированный вольфрам) – корпус узла (обойма из меди)» [3]. Здесь при строгой постановке диффузионной задачи необходим учет температурного поля, так как экспериментально показана его решающая роль в динамике выхода активатора из объема катодных структур данной конструкции. Совместное рассмотрение этих задач позволяет сформулировать обобщенную задачу электро- и тепломассопереноса в активированных электродах для решения практически важной проблемы увеличения функциональных характеристик и ресурса СПС.

Постановка задачи

Формулируемая обобщенная задача для электродных структур цилиндрической симметрии (рис. 1. [2]) предусматривает решение системы из трех нелинейных уравнений в двумерном приближении:

• а)    уравнения теплопроводности

  d T 1 д с к Р . . ,=-т- d t r д r

  
  

  .     . ^дТ-

  r ^ k ^{( Т} - )— д r

  
  

  + х (Т - )

  
  

  д Т

  
  

  д z

  
  

  + Г2/ ^ к (Т - );

  
  

• б)    уравнения непрерывности тока

  1 д r д r

  
  

  r^ k ^{( т} - )

  
  

  д U - д r

  
  

  д

  + — дz

  
  

  ^ к ^{( Т} - )

  
  

  д U - дz

  
  

  = 0 ,

  
  

j- =(j2 + jT,   Jr =—^k № I5r,   jz =-at (T-)cUk I & для катодного узла (к = 1 - катод, к = 2 - обойма);

• в)    уравнения диффузии для катода

  д n д t

  
  

  1 д r д r

  
  

  д

  + — дz

  
  

  д n

  дz ’

  
  

D (Tk) = D oexp(-Q^), kTk где Tk - температура; ck, pk, Xk, оk - соответственно удельная теплоемкость, плотность, коэффициент теплопроводности, удельная электрическая проводимость материалов катодного узла ; jk - плотность тока; Uk -потенциал электрического поля; n, D, D0, Qa, - соответственно концентрация, коэффициент диффузии, фактор диффузии, энергия активации легирующего элемента (присадки); k -постоянная Больцмана; t - время. Решение этих уравнений с соответствующими граничными условиями проведено в [1, 4].

В данной задаче решение ищем в два этапа. Сначала ставится тепловая задача и методом установления определяется стационарное температурное поле Т 1, ₂ ( r , z ) в катодном узле в целом. Затем, используя полученное распределение Т 1, ₂ ( r , z ) на пространственно-временной сетке тепловой задачи численным методом конечных разностей по локально-одномерной схеме прогонки, находится поле концентрации во вставке n ( r , z ).

Результаты расчетов и обсуждение

При численном моделировании процессов диффузии и испарения активатора наиболее важным параметром является коэффициент р, характеризующий долю атомов, возвратившихся на катод в результате рециклинга [1]. В процессе счета коэффициент р варьировался от 0 до 1. Соответствующим выбором значений р можно моделировать различные режимы работы катода. Например, режим при р=0 (свободное испарение без учета ионно-атомного рециклинга) соответствует неустановившемуся режиму работы катода в момент поджига или отключения дуги, когда происходит наиболее интенсивный унос материала присадки с рабочего торца. Теоретически безэрозионный режим работы катода может быть достигнут, когда в месте привязки дуги устанавливается динамическое равновесие между испарением с поверхности и возвратом активатора в виде ионов (п=1). В данном случае, характеризующемся эффективным механизмом рециклинга, по истечении 60 мин концентрация эмиссионного компонента в пятне составила величину 0,92 от первоначальной, в то время как концентрация за пятном уменьшилась до 0,17. Здесь ресурс работы катода в течение одного включения плазменного устройства оп -ределяется динамикой выхода и испарения присадки за пятном и с боковой поверхности. Расчетное содержание присадки в месте контакта дуги с катодом получается наиболее близким к экспериментальному при п = 0,9 - 0,95.

Влияние длины вылета катода из обоймы L c на динамику выхода активатора из объема электрода проанализируем на примере торцевого ( L c = 0) и стержневого ( L c = 1 см) катодов, рассмотренных в тепловой задаче [2]. По аналогии с графиками изотерм построим линии равных концентраций в объеме электрода .

На рис. 1. показаны кривые изоконцентраций n / n ₀ ( n , n ₀ - текущая и начальная концентрации) в полуплоскости осевого сечения электродных узлов (I - катод, II - обойма). Распределения, полученные для торцевого катода (рис.1 а), по характеру напоминают его изотермы. Они имеют вид таких же плавных линий, плотно охватывающих область горячего пятна.

В стержневом катоде (рис. 1б) конфигурации кривых изоконцентраций кардинально изменяются. Здесь они сгущаются не в зоне катодного пятна, а на периферии рабочего торца электрода, что связано с более интенсивным обеднением присадкой боковой поверхности электрода. В области же пятна испарение активатора компенсируется возвратом его в виде ионов на катод. В торцевом катоде характер выхода активатора на рабочую поверхность и соответственно распределение n ( r, z ) внутри электрода совершенно другие. Здесь унос присадки происходит в основ -ном с поверхности катодного пятна. Этот факт можно объяснить следующими причинами.

Во-первых, из-за высокой температуры в пятне и его окрестности ( Т > 3400 K) скорость испарения материала в этих местах резко возрастает. Во-вторых, при таком уровне температуры происходит интенсивный рост зерен матрицы вольфрама (рекристаллизация), что существенно уменьшает диффузионный поток присадки из более удаленных слоев катода. В расчетах процесс рекристаллизации учитывался тем, что в диапазоне от 2900 К до температуры плавления матрицы коэффициент диффузии уменьшался (~ до 2 порядков) обратно пропорционально температуре электрода [5]. Рассмотренные выше факторы вызывают быстрое обеднение активирующим элементом области пятна торцевого катода. В стерж-107

невом катоде уровни температур ниже и профиль их имеет более пологий и плавный характер [2]. Этим обеспечивается равномерная и эффективная подпитка рабочей поверхности активатором. Кроме того, как видно из рис. 1 б, диффузия осуществляется из более удаленных и обширных областей, чем в катоде с L c = 0.

В силу этих причин работоспособность катода значительно увеличивается. Таким образом, можно сделать вывод о том, что применение активированных тугоплавких металлов эффективно в катодных узлах с большими объемами равномерно прогретой части электрода с достаточно высокой интегральной температурой, когда L c / d 1 >> 1 ( d 1 - диаметр катода).

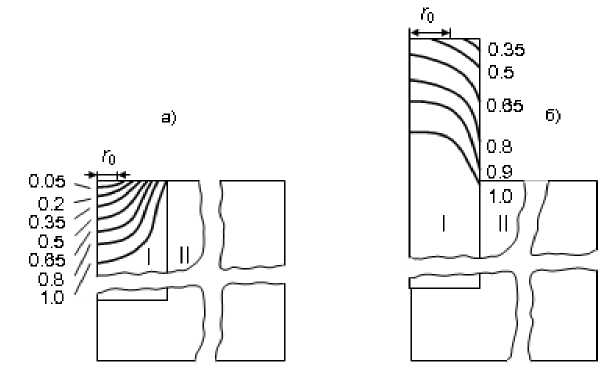
Рис. 1. Изоконцентрационные линии в торцевом (а) и стержневом (б) катодах. I = 600 A, t = 20 мин

Проанализируем динамику уноса активирующего элемента с рабочих поверхностей рассматриваемых электродов в процессе их функционирования.

На рис. 2 показаны распределения присадки по рабочей поверхности этих катодов после 5 мин их работы. На поверхности торцевого катода в пределах опорного пятна разряда r ₀ = 0,15 см концентрация за это время уменьшается больше, чем на порядок (кривая 1 ). При этом наиболее интенсивное обеднение происходит в области, непосредственно прилегающей к пятну. Аналогичная картина наблюдается и на стержневом катоде L c =1 см с опорным пятном r ₀= 0,31 см (кривая 2 ).

Однако здесь уровень концентрации активирующего элемента значительно выше ( n / n о > 0,6), а профили распределения по поверхности более равномерные.

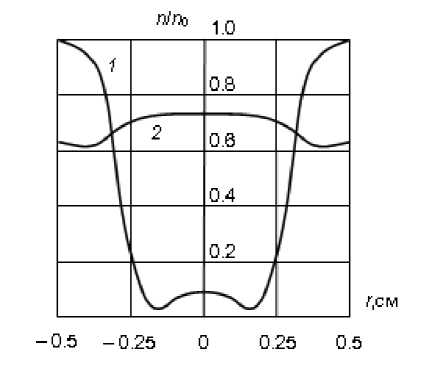
Рис. 2. Распределение активатора по диаметру рабочей поверхности торцевого ( 1 ) и стержневого ( 2 ) катодов

После 10 мин работы присадка в центре горячего пятна торцевого катода полностью исчезает (рис. 3, кривая 1 ), а на стержневом катоде к этому времени устанавливается постоянный уровень концентрации n / n ₀ = 0,63 (кривая 2 ), т.е. наступает динамический баланс между потоками поступающей и расходуемой присадки. Аналогичное явление происходит и на боковой поверхности электрода (рис. 4), но здесь равновесие наступает примерно после 15 мин работы катода. В дальнейшем на всей рабочей поверхности электрода содержание активирующей присадки не изменяется.

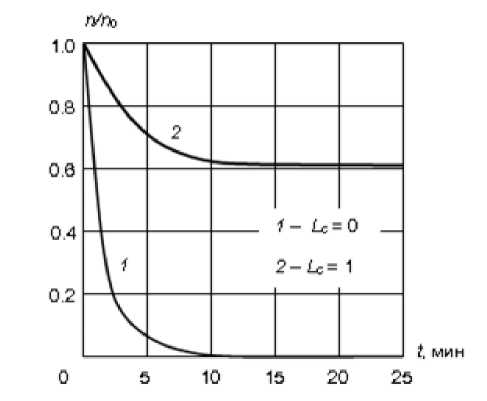
Рис. 3. Зависимость концентрации активатора в центре рабочих поверхностей катодов от времени

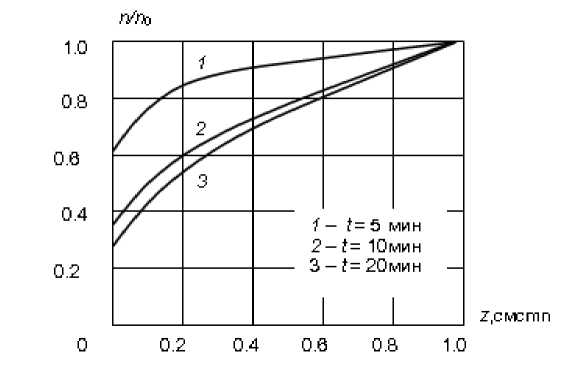
Рис. 4. Распределение концентрации активатора по цилиндрической поверхности стержневого катода

Такая динамика выхода и уноса активатора из катода объясняется тем, что в расчетах не учитывались изменения эмиссионных свойств и теплофизического состояния электрода в процессе функционирования, влияние этих факторов на характер перераспределения частиц легирующего металла в объеме и на поверхности матрицы.

Заключение

Поставлена и решена в двумерном приближении задача тепломассопе-реноса эмиссионно-активирующих элементов термокатодов цилиндрической геометрии. В совместной постановке решены нелинейные уравнения теплопроводности и протекания тока, диффузии и испарения легирующих компонентов. Анализируются особенности тепломассопереноса активатора в объеме матрицы. Промоделированы и изучены различные режимы его выхода из катода. Показано, что на динамику данного процесса существенное влияние оказывают процесс рекристаллизации материала электрода и механизм рециклинга атомов и ионов металла в прикатодной области стационарного дугового разряда. Исследованы закономерности те-пломассопереноса активирующих элементов в зависимости от теплового состояния и геометрии катодного узла. Установлено, что эмиссионные характеристики электродов главным образом зависят от температурного режима катодного узла.