Анализ решений нелинейного уравнения Матье-Хилла с учётом собственного тока резонансного контура

Введение. Нелинейный параметрический эффект широко используется в электронике для создания малошумящих усилителей и высокоэффективных генераторов, элементов памяти, логических элементов – регистров, счетчиков, дешифраторов, сумматоров и функциональных преобразователей и др. Применение электронной аппаратуры, имеющей в своем составе нелинейные резонаторы, чрезвычайно широко. Нелинейные резонаторы представляют собой колебательные параметрические зонные (или пазонные) системы, работающие в первой или высших зонах неустойчивости колебаний, на высших гармониках.

Резонансные схемы, использующие колебательные контуры, представляют собой нелинейно-параметрические зонные (пазонные) системы (НПС). Они широко используются в качестве высококачественных усилителей, генераторов, преобразователей, а в цифровой технике – триггеров, логических элементов и элементов памяти. Их применение позволяет не только улучшить технические характеристики электронной аппаратуры, но и повышает их надежность в условиях неблагоприятного воздействия окружающей среды. Достоинства таких систем обусловливают их использование в измерительной технике, в качестве датчиков НЧ-диапазона как малошумящих функциональных устройств.

Постановка задачи. Изучение свойств и закономерностей явлений в НПС, работающих в высших зонах неустойчивости, весьма актуально и возможно при разработке точных методик и широкого класса экспериментальных методов. Подобные исследования лежат в плоскости наноэлектроники при изучении нелинейных параметрических резонансных явлений в наноразмерных структурах.

Методы и результаты исследования. Нелинейно-параметрические взаимодействия распространены в природе очень широко и присущи многим нелинейным средам. Колебательные процессы в НПС удобно моделировать с помощью нелинейных электрических цепей, в которых легко получить, описать и исследовать все явления и процессы, связанные с нелинейнопараметрическими взаимодействиями. Нелинейная пазонная система индуктивного типа в общем случае описывается нелинейным дифференциальным уравнением [1]:

^_j^fL + 26 ( t , i ( t )) x ^^ + ю ₀² ( t , i(t )) x i ( t ) = 0,

-

соответственно

J 2                 X ' X Z Z           J              О X ' X Z Z        X Z'

dtdt dL (t, i (t))                                        d2 L (t, i (t))

где 5(t,i(t)) =----dt----+--------- и ®o2 (t, i(t)) = dt"     +

L(t,i(t))    2L(t,i(t))                        L(t,i(t))     L(t,i(t))x C коэффициент затухания и квадрат частоты собственных колебаний резонансного контура.

Для решения уравнения (1) предположим, что влияние собственного тока резонансного контура параметрического преобразователя на рассматриваемую систему отсутствует. Тогда оно преобразуется к уравнению:

d 2i(Udi(U

+ 2 8 ( t ) -i^tl + ro ²( t ) x i ( t ) = 0 .

dtdt

Используя подстановку i ( t ) = Y x e ^ ^{8 (} t ) ^-t , его можно преобразовать к виду:

+ F2(t)xU = 0, где F2(t) = го0'(t)-82(t)- —

-t2                       де           0              -t

При исследовании НПС индуктивного типа кривую намагничивания сердечников катушек индуктивности часто считают безгистеризисной и аппроксимируют гиперболическим синусом [1, 2]. Тогда ток в цепи накачки в случае, если параметрический преобразователь подключен к генератору с напряжением U ( t ) = U m cos rot , определяется следующим образом:

αl

(t) = — x sh

H

fe

( 2 SWro

) sin( rot )

J

В работах [1, 2] было показано, что изменение индуктивности одного сердечника резо- нансного контура будет иметь вид:

L (t) =

^L 0

ch (b sin( rot))

SW ²

b = ^e m приведен-

2 SWro

где Lq =--индуктивность резонансного контура при i(t)=0; αβl ная амплитуда тока накачки; W- число витков обмотки накачки; 5, l - площадь поперечного сечения и длина средней линии сердечника; ω – круговая частота напряжения накачки.

На практике большой интерес представляет НПС индуктивного типа, в которой затухание очень мало, т.е. сопротивление активных потерь значительно меньше реактивных сопротивлений: ( R << X L , R << X C ).

Предположим, что R = 0 (потери в системе отсутствуют). В этом случае:

X L X t ) ^{8 (} t ) = VTT^{; e}

L ( t )

—

1                           1

; ^{F (} t ) = 77777 = ^ro 0 ^{x ch (} b ^{sin rot} ) L ( t )             L ( t ) C

1 где   го д =---- представляет собой квадрат собственной частоты резонансного контура

L 0 C

НПС при отсутствии модуляции индуктивности.

Функция F ² ( t ) имеет физический смысл квадрата круговой частоты собственных колебаний резонансного контура. В дальнейшем для решения уравнения (2) с учётом (3) используем следующее разложение:

ch(b sin rot) = 10 (b) + j^ (—1)k 12k (b) x cos(2krot), k=1

где I 2 k ( b ) – модифицированные функции Бесселя чётных порядков.

В случае R = 0 уравнение (2) имеет вид:

—- + ® 0 ² ( 1 0 < b ) + 2 ^ ( - 1) ^к X 1 2 к ( b )cos(2 k _Ю t))U = 0. dt                   к = 1

Сделав замену переменной ω t= τ , получим уравнение Хилла в виде:

d U f ^ )

+1 ⁰ I dT ² к to 7

№

\

X 1 ₀( b ) + 2 у ( - 1) ^kI 2 k ( b )cos(2 кт ) U = 0

.

к

к = 1

Для решения уравнения (4) можно применить метод Уиттекера, согласно которому № необходимо, чтобы ряд У12к(b) <№ сходился [3].

к = 0

Докажем сходимость этого ряда. Известно, что

№

10( z) + 2 У (-1) к12 к (z) = cos( Z), к=1

где I n ( z ) – модифицированные функции Бесселя порядка n [4].

Прибавив в последней формуле к обеим частям I 0( z ), получим: №

2 ^ ( - 1) ^к1 2 к ( Z ) = cos( z ) + 1 0 ( Z ).

к = 0

Заменив в последнем выражении z на ix , а также используя известные формулы

I n ( ix ) = iⁿI_n ( x ) и cos (ix) = ch(x) , окончательно получаем:

_:г I , к ( x ) = £h * x ) +/0 ( x ) к = 0                   ²

•

№

Таким образом, ряд ^ 1 2 к ( b ) <№ сходится.

к = 0

Применим метод Уиттекера для решения уравнения (4). В случае малости коэффициентов при сомножителе cos(2k τ ) можно получить достаточно хорошее приближение, используя три центральных строки и три центральных столбца определителя Хилла бесконечного порядка [3].

Для уравнения Хилла d ^U + F ²( т ) x U = 0 чаще всего рассматриваются два случая, в dT ²

одном из которых функция F ² ( т ) имеет вид:

F\т ) = 0 ₀ + 20 cos(2 t ) + 2 0 2 cos(4 t ) + ... ,

№ где коэффициенты 0n - заданные постоянные, и ряд У Оn абсолютно сходится.

n = 0

Положив θ -n = θ n , ищем решение уравнения Хилла в виде:

№

U = е ^ ^т У а„е ^{2 niT} ,

n n = -№ где µ – характеристический показатель.

Для определения амплитуды a n имеем систему уравнений:

»

( ц + 2 ni ) ² a n + ^ O m a n - m = 0 ( n = ..., - 1,0,1,...) .             (6)

m =-«

Для определения µ составляется определитель Хилла Δ(iµ). Известно [5], что корни опре- делителя Хилла являются корнями уравнения:

I niu ]

sin ² I —— I = A (0) sin

I 2 )

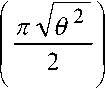
поэтому необходимо найти A ( 0 ) , а затем из (7) найти ц .

Для количественного анализа решения уравнения Хилла ограничимся только коэффициентами O o , O ₁, O ₂, так как при большом количестве коэффициентов O m решение становится неоправданно громоздким при незначительном возрастании точности. Отбрасывание остатка ряда (5) при вычислениях производится исходя из условия O m >> O _m+1 (m>1).

Рассмотрим случаи, когда приведённая амплитуда тока накачки принимает следующие значения: b =1; 1,6; 2,2; при —°- = .

ω 2

В случае b =1, ю =2 ю о находим следующие значения: A ( 0 ) =1,002; ц = -0,563i. Подставив найденное значение ц в (6) и положив O _-1 = O ₁, получим:

-4х ( n -0,282 ) 2 х a n + O 1 х ( a n _{+ 1} + a n - 1 ) + O _o х a n = 0.

Приняв значения n равными 0, 1, -1, получим однородную систему из трёх уравнений с пятью неизвестными. Положим a 2 = a -2 = 0. Тогда получим однородную систему трех уравнений с тремя неизвестными, в которой свободной переменной будет a 0 . Решив эту систему, получим:

a -1 = – 0,005 a 0 , a 1 = – 0,019 a 0 .

Таким образом, величину амплитуды колебаний определить нельзя. Это подтверждает тот факт, что теория линейных дифференциальных уравнений с периодическими коэффициентами не может дать ответа на вопросы о величине стационарной амплитуды, процессе ее установления и т.д. [1, 2, 6].

Положим a 0 = –1. Тогда: a -1 = 0,005, a 1 = 0,019. Подставив значения a 0 , a 1, a -1 и взяв мнимую часть, находим искомую функцию U ( т ):

U ( т ) = sin ( 0,563 т ) + 0,019 х sin ( 1,437 r ) - 0,005 х sin ( 2,563 т )

Ток i ( т ) равен:

ch ( b sin τ )

i ( т ) = U ( т ) х------------ .

L ₀

С учетом (8) окончательно получаем выражения для тока i ( т ) во всех случаях.

При b = 1 и ю = 2 ю ₀ получим:

i ( т ) = —(1,269sin(0,563 т ) + 0,161 х sin(1,437 т ) - L 0

• -    0,143 х sin(2,563 т ) - 0,005 х sin(3,437 т ) + 0,003 х sin(4,563 т )).

При b = 1,6 и ю = 2 ю ₀:

i (т ) = —(1,78 sin(0,67 T ) + 0,52 x sin(1,33 T ) - ^L 0

• -    0,39 x sin(2,67 T ) - 0,05 x sin(3,33 T ) + 0,02 x sin(4,67 T )).

При b = 2,2 и ω = 2 ω 0 :

i (т) = — (2,97 x sin(0,87T) +1,81 x sin(1,13т) - sin(2,87T) -L0

• -    0,39 x sin(3,13 T ) + 0,1 x sin(4,87 T ) + 0,03 x sin(5,13 T )).

На рис.1 приведены в нормированных единицах графики функций i = i ( т ) для значений b =1, 1,6 и 2,2. Из графиков видно, что в областях устойчивого решения уравнения Хилла установившиеся параметрические колебания существовать не могут. В этих областях наблюдаются случайные колебания с постоянно изменяющейся амплитудой и фазой, т.е., как говорят, в этих областях нелинейный резонатор НПС индуктивного типа «шумит».

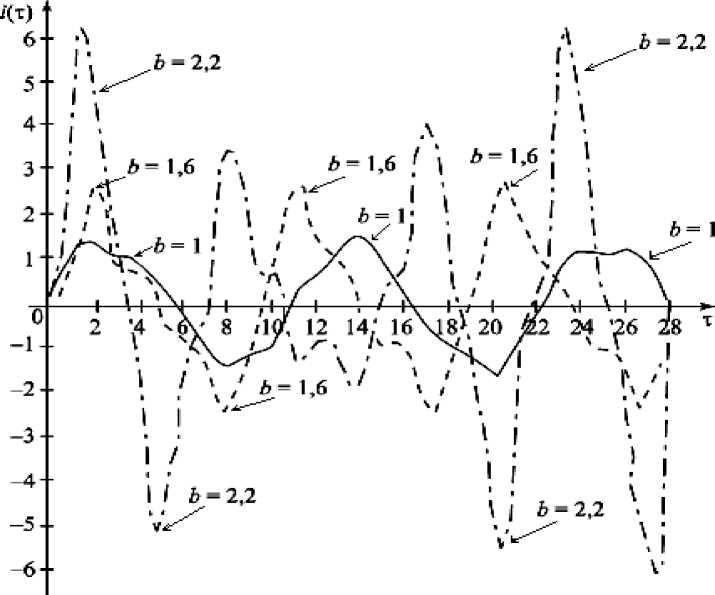
Рис.1. Кривые, описывающие механизм усиления тока в резонансном контуре при увеличении приведенной амплитуды тока накачки b. Обозначения на рис.: b=1 – сплошная линия;

b=1,6 – пунктирная линия; b=2,2 – штрихпунктирная линия

В работах [1, 2] был рассмотрен случай питания нелинейно-параметрического преобразователя индуктивного типа от генератора напряжения. Аналогично производится расчет и в случае питания от генератора тока. Рассмотрим случай, когда генератор имеет синусоидальную форму тока:

it ( t ) = I m ^{sin( to t} ). (9)

Динамическая индуктивность контура описывается выражением [1, 2, 7]:

2 SW ²

L (t) = —,= в i 2н W 2 + a2l2

Ц( H) = -1 x

α H2

11 +'

α ²

Подставив выражение (9) в формулу (10) и сделав преобразования, получим выражение для динамической индуктивности:

L ( t ) =

2 L 0

W2I2    2         , з m sin2 (tot) +1 l2α2

SW ²

^{где L} 0      ,

αβl

.

Обозначим

W ² I m ² l ² α ²

= 2 m ² . Применив соотношение 2sⁱn ^{2 (} ®^t ) = 1 ^— c^os^{(2 to t} ) и сделав

несложные преобразования, получим:

~

L (t) = I 2 0•

m ² cos(2 ω t )

J 12----

\1

~2

где ^L 0 = "T==.

V1 + m ²

В случае R =0 (для системы без потерь) для квадрата круговой частоты собственных колебаний резонансного контура F ² ( t ) выше была получена формула (3). Тогда с учётом выражения (12):

F ²( t ) = ¹ ® 2 '41 + m ^{2 -}з /1 — m—т cos(2 tot ).

2 0          V 1 + m

Отсюда, в случае питания параметрического преобразователя от генератора тока, уравнение (4) преобразуется к виду:

d²U 1 f to Y R 2   1 m ²cos(2 t )       _

+ -I I V1 + m² -3 1 U = 0.

dT    2 V to )           V 1 + m

Воспользуемся известной формулой биноминального ряда:

-       n ( n - 1) 2 n ( n - 1)( n - 2) з

(1 + x ) ⁿ = 1 + nx + —---- ^x ² + '---- Л---- Lx ³ + ...

2!                   3!

Применив эту формулу и подставив значение для переменной x x =

m ² cos(2 τ )

1 + m

получим следующее уравнение для определения напряжения U:

2 2 d U 1 f to g ] /i     2 + I - I V1 + m	1 m 2 cos(2 t )   1 1           -	m 2 cos(2 t ) ^	2      1 — I	x U = 0
dT 2    2 V to )	2   1 + m 2      8	V 1 + m 2 )	J

В уравнении (13) ряд, представленный в квадратных скобках, сходится для любых значе- m2 cos(2τ)

1 + m ²

ний m и τ , так как

< 1

.

Рассмотрим решение уравнения (13) для значений: —0 = 0,9; Im = 103 -10 3A (при ω m=2,444). После подстановки исходных данных получим:

d 2 U + (1,0204 - 0,458 cqs(2 t ) - 0,046 cqs(4 t ) - ...) x U = 0.

dτ ²

Ограничимся для анализа следующим уравнением, в котором для F ² ( t ) учтены только два слагаемых ряда, так как большее количество слагаемых приводит к громоздким вычислениям при незначительном увеличении точности:

dU + (1,0204 - 0,458cqs(2 t )) x U = 0                      (14)

dτ ²

Найдем неустойчивое решение уравнения (14), соответствующее первой области неустойчивости, используя метод Уиттекера [3], согласно которому общее решение уравнения Матье

y-+( + (a - 2q cqs(2t)) x у = 0

dτ ²

может быть записано в виде:

у = A1 ецт x Ф(т, о) + A2e-“; x Ф(т,-о), где A1, A2 – произвольные постоянные; µ – характеристический показатель; σ – параметр, прини-π мающий для неустойчивых решений значения между 0 и - "2 .

Функция Ф ( т , о ) имеет для первой области неустойчивости следующий вид:

Ф (т,о ) = sin( T - о ) + S з sin(3 T - о ) + C 3 cqs(3 t - о ) + ...,

1      1

где S ₃ = — q + — q ²cqs(2 t ) + ... , а ^C 3 = y q ^sin⁽2 ^o ) + ... .

• 3    8    64

Для определения □ имеем уравнение:

• —q ²(1 - q )cqs²(2 o ) - q (1 - — q ²)cqs(2 o ) + ^ q ⁴ -2 q ² + 1 - _a = 0.

  
  

  4       64                 64             15368

Для уравнения (14) q =0,229. Из уравнения (15) находим, что σ =–0,872. Тогда для µ , S 3 , C 3 получим следующие значения: µ =0,113; S 3 =–0,029; C 3 =–0,002. Ограничимся точностью вычислений, равной 3 x 10^-3 (считаем С₃ =0), тогда:

Ф( т , о ) = sln( T + 0,872) - 0,029 sln(3 T + 0,872) .

Отсюда находим функцию y ( τ ):

у ( т ) = A 1 е 0, ^{113 т} [ sin( T + 0,872) - 0,029sin(3 T + 0,872) ] + + A ₂ e ^{- 0,113 т} [ sin( T - 0,872) - 0,029sin(3 T - 0,872) ]

Считая, что y (0) = 0, из (16) получаем А 1 = А 2 .

Постоянные ^{A 1} , ^{A 2} имеют физический смысл амплитуды начальных колебаний в ре- L 0 L 0

зонансном контуре НПС индуктивного типа. Для реальных систем, работающих в первой об- ласти неустойчивости, можно принять

A ¹ = A ² = 10 ³ A . Тогда, учитывая, что i(т ) = y(^{T )} ,

L 0 L 0                                          L ( τ )

получаем:

i ( т ) = WT VIW X, 1

2 L

—

m ² cos(2 τ )

1 + m²

.

Взяв два слагаемых ряда (при m = 2,444), окончательно получим для тока i ( т ):

i(т ) = 1,32 X { е^0Д13т [ sin( т + 0,872) - 0,029 sin(3 т + 0,872) ] +

L 0 (17) + е ^{- 0,113 т} [ sin( T - 0,872) - 0,029 sin(3 т - 0,872) ] } x (1 - 0,428 cos(2 т )) x 10 ^{- 3}.

Полученное решение (17) не учитывает влияние собственного тока резонансного контура НПС на модуляцию индуктивности L ( t ) этого же контура. Это не позволяет математически точно описать процессы установления колебаний в резонансном контуре системы после достижения ими некоторой величины, определяемой, в основном, нелинейностью параметрической системы.

Для устранения этой проблемы воспользуемся методом последовательных приближений, описанным в [8, 9], и с учетом влияния собственного тока резонансного контура параметрической системы на модуляцию его индуктивности, получим выражение для суммарной индуктивности:

L^{( T} ,i^{( T ))} =

'                  1                  '

J[ z „ ± i ( т ) ] ² W ² + a ² l ¹ ,

X

2 SW ²

β

Величина 2m2 с учетом первой гармоники (как имеющей наибольшую амплитуду по срав- нению с высшими гармониками) будет иметь вид:

2 m 2 = W! I m ± dA 1 (^е "  ^{+ е} " " ⁾

l ² a ^{2             2} L 0

В последних полученных выражениях ток i(т) может как суммироваться, так и вычитаться с током Im. Это обусловлено схемными особенностями параметрических преобразователей индуктивного типа, у которых резонансная обмотка на одном сердечнике включена согласно с обмот- кой накачки, а на другом встречно [1, 2, 10, 11]. Учитывая это, суммарная индуктивность L(т, i(т)) и величина 2m2 будут равны:

L ( τ , i ( τ ))

SW ²

г

^в _V-\j [ iH + i(т ) ] ² w ² + 1 ² a ²    д/ [ z'h - i(т ) ] ² W ² + 1 ²a²

2 m ²

2 W ²

l ² α ²

I m

V

;

У

Коэффициент

d

в (18) определяется

d ² A ²

⁺—jb ch _цт .

L 0        У в начале каждого периода

из выражения

² , где

m(0) – величина m, вычисленная в точке, где Im = 0. Такое вычисление коэффициента d вполне оправдано, так как этот коэффициент в течение полупериода изменения индуктивности изменяется медленно.

Вычисление i ( т ) по выражению (17) с учётом влияния собственного тока резонансного контура системы производится до момента перехода решения уравнения (13) из области неустойчивости в область устойчивости. Дальнейшее вычисление i ( т ) производится по устойчивому решению уравнения (13).

На рис.2 и рис.3 приведены расчетная и экспериментальная кривые нарастания и установления колебаний тока в резонансном контуре параметрического преобразователя индуктивного типа, имеющего следующие конструктивные характеристики: 30 витков в обмотках накачки и резонансных обмотках; сердечники К7 х 4 х 2 из феррита 1500 НМ и ёмкость конденсатора резонансного контура С = 0,2 мкФ.

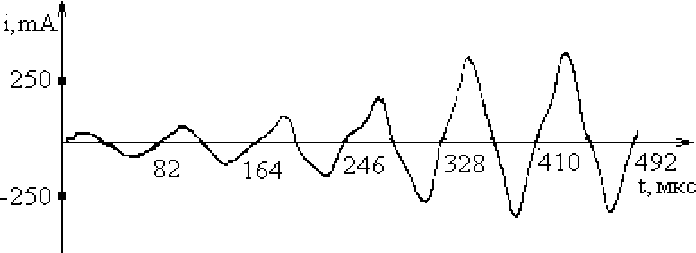
Рис. 2. Расчетная кривая нарастания тока в резонансном контуре

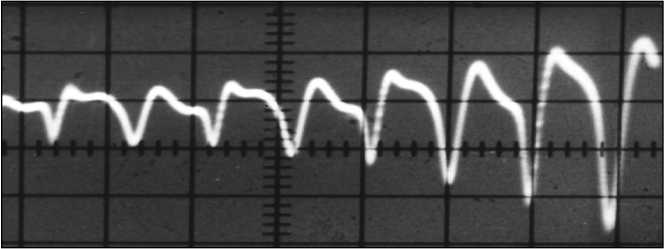
Рис. 3. Экспериментальная кривая нарастания тока в резонансном контуре

Установившееся значение тока резонансного контура для данного параметрического преобразователя рассчитывалось по выражению, являющемуся устойчивым решением уравнения (13) с учетом (19):

i (т) = -^- ( sin( r ) - 0,026sin(3 r ) ) х (1 - 0,428cos(2 r )), 2 L 0

где I 0 – амплитудное значение тока собственных колебаний контура в момент перехода решения из области неустойчивости в область устойчивости.

Аналогично рассмотренному выводу выражения (17) при питании параметрического преобразователя от генератора тока для случая его питания от генератора напряжения такое решение имеет вид:

i ( т ) = X { е 0.055 г [ _sin( _r + 0,898) _ 0,014sin(3 r + 0,898) ]+

L ⁰                                                                       (21)

+ е ^-°’^{055 г} х [ sin( r - 0,898) - 0,014 sin(3 r - 0,898) ] } х (1,26 - 0,28 cos(2 r )) х 10 — ³.

Выводы. Таким образом, при нахождении только устойчивого решения уравнения Матье – Хилла методом Уиттекера амплитуду колебаний в резонансном контуре НПС индуктивного типа определить не представляется возможным. Для её определения необходимо найти и учесть неустойчивое решение уравнения. Сопоставляя выражения (17) и (19) для тока при питании параметрического преобразователя от генератора тока и генератора напряжения , следует отметить, что ток в резонансном контуре нелинейно-параметрической зонной системы нарастает быстрее в случае её питания от генератора тока. Выражения (20) и (21) определяют решение нелинейного дифференциального уравнения Матье-Хилла с учётом установившегося значения собственного тока резонансного контура для изучаемого параметрического преобразователя.

Результаты работы представляют значительный теоретический и практический интерес для проектирования радиоэлектронных систем.