Анализ теплофизических свойств почв криолитозоны по данным мониторинга вертикального профиля температуры

Широкий интерес к освоению Арктической зоны Российской Федерации (АЗРФ) обусловлен как сосредоточенными в ней значительными природными ресурсами, так и стратегическим значением для развития транспортной инфраструктуры и возможностями для социальноэкономического развития регионов. При размещении промышленных и инфраструктурных объектов необходимо учитывать возможные риски для экосистем Арктики. Результаты многочисленных наблюдений показывают заметные изменения характеристик экосистем криолитозоны в последние десятилетия, связанные прежде всего с потеплением климата [1–3]. Эти изменения, в свою очередь, требуют адаптации инфраструктурных объектов и стратегии развития АЗРФ [3, 4]. Масштабное освоение северных территорий может привести к усилению деградации многолетней мерзлоты и изменению всей структуры ландшафтов.

В настоящее время на севере Средней Сибири на территории Таймырского (ДолганоНенецкого) автономного округа наиболее освоенным является Норильский промышленный район (НПР). Нарушение здесь природного состояния криогенных грунтов в результате антропогенных факторов приводит к изменению их структурных и тепловых свойств, что негативно сказывается на устойчивости экосистем и экологической безопасности. Для решения задач экологического мониторинга возрастает необходимость изучения теплофизических характеристик криогенных почв и разработки методов диагностики и прогнозирования их изменений. Особенно актуально это в связи с ростом числа техногенных аварий и нарушений в зоне вечномерзлых грунтов Таймыра и НПР.

Надежное прогнозирование состояния нарушенных криогенных почв требует выполнения расчетов многомерной динамики тепло- и влагопереноса с применением фундаментальных моделей переноса тепла и влаги. Формулирование моделей невозможно без детальных данных о теплофизических свойствах почв, дифференцированных по горизонтам и заданных в зависимости от удельного влагосодержания. Большое количество таких данных получено и сведено к эмпирическим зависимостям от структуры, состава и влагосодержания [5, 6], однако их применимость в конкретных условиях нарушенной почвы может быть необоснованной. Используемые зависимости должны быть верифицированы результатами измерений, независимо выполненных для почв данной локации. Отдельно говоря о коэффициенте теплопроводности почвы, нужно отметить предпочтительность определения этого свойства в натурных условиях [7]. При этом использование специализированных приборов для определения теплопроводности осложнено тем, что сенсор прибора неизбежно вносит возмущение в структуру почвы, а также создает локальное возмущение влагосодержания в своей окрестности, что отражается на результатах измерений [8, 9].

Актуальной является задача отработки методов определения коэффициентов теплопроводности (и связанных с ними коэффициентов температуропроводности) в натурных условиях, свободных от отмеченных факторов погрешностей. Существует широкий класс таких методов, основанных на обработке данных длительного мониторинга температуры почвы, проводимого для набора глубин на данной локации. Установка оборудования для измерения температур на различных глубинах в минимальной степени возмущает температурное поле почвы. В то же время восстановление коэффициентов теплопроводности из данных мониторинга температуры представляет собой сложную задачу, для решения которой существует множество подходов, каждый из которых имеет свои преимущества и недостатки.

Настоящая статья посвящена изучению теплофизических характеристик криогенных почв Норильского промышленного района. Непосредственной задачей исследования является разработка метода восстановления теплофизических свойств почвы путем численной обработки результатов измерений динамики суточных температур почвы на разных глубинах и выявление особенностей свойств грунтов естественных и техногенно-преобразованных почв.

Объекты и методы исследования

На территории НПР распространены два основных типа ландшафтов: равнинные лесотундровые и тундровые ландшафты, которые характеризуются низкой теплообеспеченностью, повсеместным распространением многолетней мерзлоты, невысокой биологической продуктивностью растений. Почвы НПР криогенные, представляют собой сложную систему с высоким уровнем антропогенного воздействия.

Почвенный покров на исследуемой территории представлен в основном криозёмами, сформированными в условиях вечномерзлых грунтов, определяя особенности растительности и гидрологических процессов. Поверхностные горизонты криозёмов, торфяные или грубогумусовые, обладают низкой зольностью, высокой пористостью, высоким влагосодержанием, что определяет низкую теплопроводность этих почв.

Натурные данные многодневного мониторинга температур почв были выполнены в 2023 и 2024 гг. на двух равнинных тундровых участках, на которых распространены наиболее характерные для данной территории типы криогенных почв. Первый участок, расположенный вблизи р. Боганиды, соответствует естественному состоянию почвы (участок 1, рис. 1а), второй представляет собой техногенно-трансформированную почву и расположен у р. Амбарная (участок 2, рис. 1б).

Морфогенетическая характеристика почв приведена в табл. 1. Измерения динамики температуры производились контактным методом с использованием измерителей-регистраторов температуры (логгеров) EClerk-M-2Pt, на металлическом зонде которых расположены два датчика измерения температуры на расстоянии между собой 10 см, с 06.08.2023 г. для участка 1 и с 08.09.2024 г. для участков 1 и 2.

аб

Рис. 1. Почвенные разрезы в местах установки дата-логгеров для измерений температуры, 2024 г.: а) участок 1, фоновая почва; б) участок 2, техногенно-нарушенная почва

Fig. 1. The soil sections near the locations of the temperature loggers installation, 2024: а) the test site 1, intact soil; b) the test site 2, soil under the technogenic impact

Таблица 1. Характеристика криогенных почв в пределах ландшафтов равнинной тундры НПР

Table 1. Characterization of the cryogenic soils within the flat tundra landscapes of the Norilsk region

Признаки трансформации экосистемы	Морфологическое описание
Торфяно-криозёмы, р. Боганида, фоновый участок 1
Нет признаков	Т (0–20 см) – подстилочно-торфяный горизонт темно бурого цвета, сложен растительными остатками различной степени разложения. Рыхлое сложение. Влажный. Насыщен корнями кустарничковых и травянистых растений. Граница перехода по цвету, структуре и содержанию органического вещества заметная. CR (20–45) см – криотурбированный, бурый, не дифференцированный, слабооструктуренный, суглинистый горизонт. CR┴ (45–50) см – мерзлый, с включениями жильного льда, не дифференцированный, серовато-бурый, слабо-оструктуренный, суглинистый горизонт
Криозёмы грубогумусовые, р. Амбарная, нарушенный участок 2
На участке многочисленные останки погибших древесных и кустарниковых растений. Мохово-лишайниковый покров погиб, сохраняется в виде сухого уплотненного слоя с высоким содержанием минеральных частиц. До 30 % площади участка занято минерализованными медальонами. В напочвенном покрове злаки, хвощ, кустарнички, мхи и лишайники отдельными куртинами в стадии начального восстановления (высота мхов 0,5–1 см)	О (0–5) см – горизонт серо-бурого цвета, сложен растительными остатками различной степени разложения. Уплотнен. С поверхности сухой. Граница перехода по цвету, структуре и содержанию органического вещества заметная. CR (5–55) см – криотурбированный, бурый, тиксотропный, не дифференцированный, слабооструктуренный, суглинистый горизонт. CR┴ (70–80) см – криотурбированный, не дифференцированный, бурый с ржавыми пятнами, слабоострукту-ренный, суглинистый горизонт

Существуют разнообразные подходы к определению теплофизических свойств почвы на основе измерения временной зависимости температуры на различных глубинах, в отсутствие данных иного рода, таких как плотность теплового потока. В целом они основаны на решении уравнения теплопроводности (1) в различных приближениях.

„дТ д(.дТ} ( — = — л— .

где С – объемная теплоемкость, Дж/м3, λ – коэффициент теплопроводности, Вт/м, T – темпера- тура, К.

В основном методы определения температуропроводности основаны на сопоставлении амплитуд и фаз суточных (или годовых) колебаний температуры на различных глубинах [10, 11] либо на аналитических [10, 12] или численных приближениях решения уравнения теплопроводности [13]. Кроме этого, развивается отдельный класс подходов построения моделей теплофизических параметров на основе машинного обучения, связанный с обработкой большого числа экспериментальных данных [14].

Наиболее распространенные методы оценки коэффициента температуропроводности основаны на допущении однородности свойств почвы при гармонической временной зависимости температуры. В этом случае амплитуда колебаний температуры убывает с убыванием вертикальной координаты, согласно первому закону Фурье, а смещение фазы колебаний определяется вторым законом Фурье. Исходя из первого закона температуропроводность а, м2/с, рассчитывается как (2):

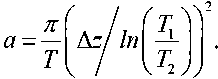
Исходя из второго – как (3):

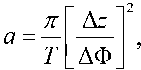
где Δz – разница по глубине между точками измерения температур, м; T 1 и T 2 , – амплитуды колебаний температуры в верхней и нижней точках, К; значения ΔΦ – смещение фазы колебаний по глубине, рад; T – период колебаний, с.

Данные методы перестают корректно работать в условиях, когда временные зависимости температуры далеки от периодических, кроме этого, полученные значения температуропроводности зачастую могут заметно различаться в зависимости от выбора конкретных данных измерений, используемых для расчетов, из всего массива данных.

В этих условиях применимы методы более общего характера, развиваемые как частный случай методов решения обратных задач теплопереноса. В настоящем исследовании использовался подход, близкий к развитому в [15].

В общем случае задача определения теплофизических свойств среды по известным временным зависимостям температуры в некоторых точках является обратной задачей теплопере-носа. В условиях данной работы постановка обратной задачи является следующей. Дан набор координат N точек измерения z i : z 1 >z 2 >…>z N , и для каждой из точек известна измеренная зависимость температуры от времени ризмер ^^ . Решая уравнение теплопроводности (1) в области z 1 > z > z N с заданными условиями первого рода на границах, соответствующих измеренным температурам, требуется определить зависимости коэффициентов уравнения от координаты и времени, λ ( z, t ), C ( z, t ), такие, что достигается минимум величины:

^^(T^zj)-!^^ . (4)

Интегрирование ведется по рассматриваемому временному интервалу. Минимально возможное количество точек – 3, и в этом случае в качестве граничных, для которых величина температуры задается в соответствии с измеренными временными зависимостями, рассматриваются первая и третья, а для второй точки производится минимизация интегрального квадратичного отклонения решения уравнения теплопроводности от измеренной температуры.

Выбран следующий метод решения описанной задачи. Весь интервал времени, в течение которого проводились измерения, разделен на интервалы длиной, равной суткам. Интервалы рассматриваются последовательно, и для каждого из них решается задача определения коэффициентов уравнения теплопроводности, которые считаются неизменными в пределах каждого интервала координаты.

Таким образом, задача определения λ(z, t), C(z, t) сводится к отдельным задачам поиска минимума функции (4). Начальное распределение температуры в первом суточном интервале задается путем линейной интерполяции данных измерений.

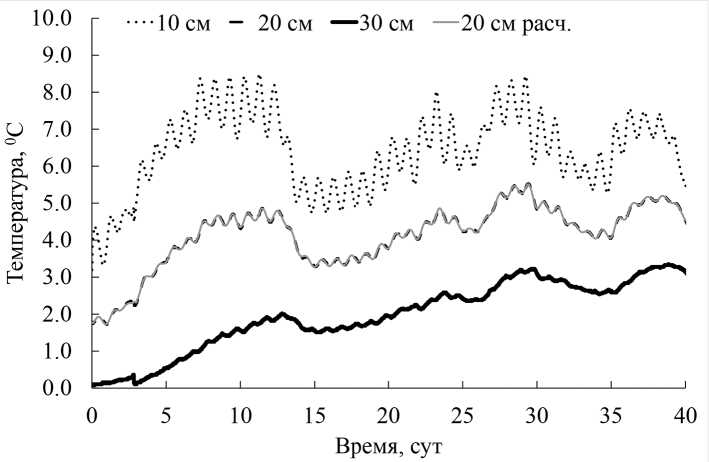
Рис. 2. Суточный ход температур почвы на участке 1 (вблизи р. Боганиды), 2024 г. Данные натурных наблюдений и расчетная температура при восстановлении коэффициента температуропроводности

Fig. 2. Daily variation of soil temperatures in the test site 1 (near the Boganida River), 2024. Field observation data and calculated temperature with the reconstructed the thermal diffusivity coefficient

На рис. 2 представлена для участка 1, 2024 г., динамика температур на глубинах 10, 20 и 30 см и рассчитанная температура на глубине 20 см в результате подбора значений λ ( z, t ), C ( z, t ) для минимизации функции (4).

Одной из особенностей почв данных участков является сохранение достаточно влагонасыщенного состояния в течение практически всего летнего периода, что предполагает меньшие колебания температуропроводности из-за изменения влажности почв. Для сопоставления рассчитанных данных приведены результаты полевых измерений температуропроводности с помощью прибора «TEMPOS» Thermal Properties Analyzer (METER Group, USA) с использованием двух игольчатых щупов SH-3 (табл. 2). В данном приборе одна из игл является источником тепла, а на второй измеряется температура, далее коэффициент температуропроводности рассчитывается на основе решения обратной задачи теплопроводности.

Таблица 2. Осредненные данные полевых измерений прибором «TEMPOS» значений коэффициента температуропроводности

Table 2. Averaged data of field measurements of the thermal diffusivity coefficient values using the TEMPOS meter device

Участок, год	1, 2024	2, 2024	2, 2024
Почвенный слой	10–30 см	0–5 см	10–30 см
∙106, м2/с (число измерений)	0,14 (4)	0,14 (2)	0,4 (6)

Результаты обработки многодневной динамики измерений температуры

Длительный период наблюдений динамики температуры на разных глубинах позволил обработать данные на основе преобразования Фурье (рис. 3, 4). Из результатов преобразования видно, что вблизи поверхности существуют две основные моды: высокочастотная мода, соответствующая суточному циклу, и низкочастотная, соответствующая колебаниям среднесуточной температуры в ходе текущего летнего периода. Наблюдаемое отклонение от 24 часов связано с дискретным шагом по частотам быстрого преобразования Фурье. С увеличением глубины амплитуда суточной моды падает, в том числе и относительно более низкочастотных мод, особенно это заметно для участка 1. Кроме того, для данного участка в торфяном горизонте на глубине 20 см даже наблюдаются небольшие колебания суточной амплитуды около 24-часового периода для 2023 и 2024 гг. Для участка 2 с нарушенной почвой остается доминирующей суточная мода на глубине 20 см, вплоть до моды, соответствующей 4 суткам. Это связано с тем, что торфяной горизонт отличается высокой пористостью и неоднородностью структуры, в то же время для трансформированного участка под небольшим органогенным верхним слоем (примерно до 10 см) на глубине 20 см расположен криотурбированный суглинистый горизонт, имеющий меньшую пористость и большую однородность. Наибольшие ам-

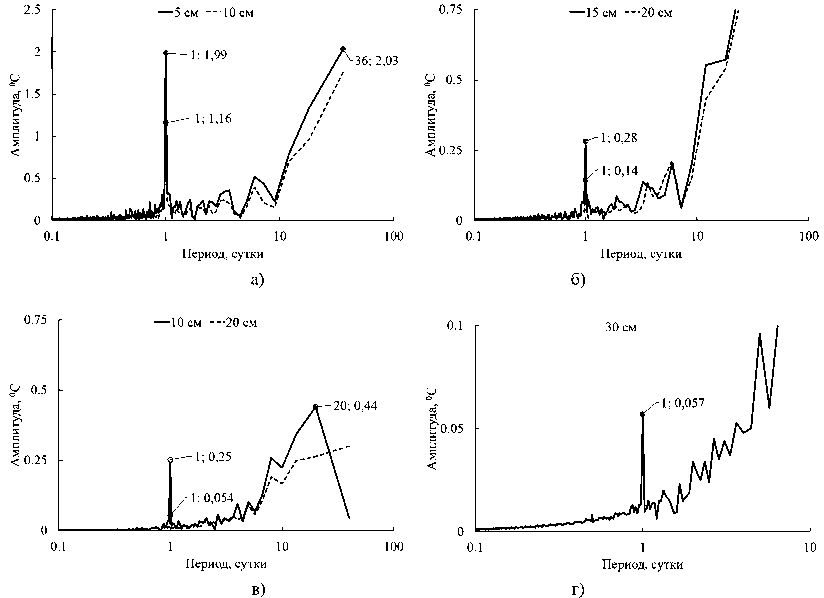
Рис. 3. Зависимость амплитуды от периода колебаний, полученная при разложении натурных данных динамики температуры на участке 1 в ряд Фурье, на глубинах: а) 5 и 10 см, 2023 г.; б) 15 и 20 см, 2023 г.; а) 10 и 20 см, 2024 г.; б) 30 см, 2024 г.

Fig. 3. The result of the Fourier transform of the temperature time dependencies obtained in the test site 1, depths of: a) 5 and 10 cm, 2023; b) 15 and 20 cm, 2023; a) 10 and 20 cm, 2024; b) 30 cm, 2024

– 1020 – плитуды, соответствующие примерно месячному периоду для 2023 г. и полумесячному для 2024 г., связаны с колебаниями среднесуточной температуры, которые, например, хорошо видны из данных натурных наблюдений для участка 1 в 2024 г. (рис. 3). Данные периоды соответствуют только конкретно текущим проведенным наблюдениям и не имеют обоснованного систематического характера.

Полученные характеристики преобразования Фурье были использованы для расчета усредненных коэффициентов температуропроводности с помощью амплитудного (2) и фазового (3) методов (табл. 3) на основе парных данных измерений температур, произведенных одним дата-логгером. Отношения амплитуд и разности фаз колебаний температур в формулах (2) и (3) соответствуют значениям реальной и мнимой частям комплексной амплитуды температуры для суточной моды, полученной при разложении в ряд Фурье соответствующих данных (рис. 3, 4). Использование данных Фурье-разложения позволяет получить усредненное значение коэффициента температуропроводности для исследуемых почв криолитозоны, что особенно оправдано в условиях доминирующего переувлажненного состояния почв в летний период, которое приводит к относительному постоянству теплопроводящих свойств почв.

Для распространяющихся в идеальных условиях гармонических колебаний, в данном случае температур, результаты на основе амплитудного и фазового метода должны совпадать. В рассматриваемом случае расхождения в значениях температуропроводности колеблются примерно от 1,5 до 5 раз. При этом наибольшие расхождения наблюдаются в переходных областях из одного почвенного горизонта в другой: в 5 раз на участке 1 (2024), на глубине 20 см – 30 см переход от торфяной к минеральной суглинистой почве; в 3 раза на участке 2, на глубине 5 см расположена граница органогенного горизонта (табл. 1). Кроме этого, можно отметить, что на участке 1 для 2024 г. происходит более быстрое затухание сигнала по сравнению с 2023 г. (рис. 3). В целом видно, что на участке 1 на глубине 5–20 см получаются близкие средние значения температуропроводности 0,14–0,19∙10–6 м2/с, что согласуется с морфологическими и физико-химическими характеристиками почвенного профиля. Результаты расчета по слою 20–30 см показывают слишком большое расхождение для возможности использования

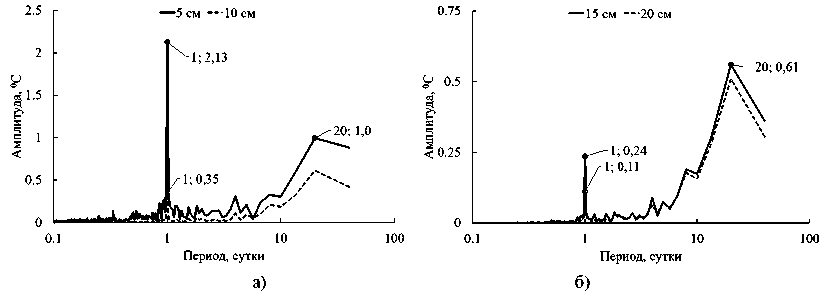
Рис. 4. Зависимость амплитуды от периода колебаний, полученная при разложении натурных данных динамики температуры на участке 2 (2024 г.) в ряд Фурье, на глубинах: а) 5 и 10 см, 2024 г.; б) 15 и 20 см, 2024 г.

Fig. 4. The result of the Fourier transform of the temperature time dependencies obtained in the test site 2 in 2024, depths of: а) 5 and 10 cm; b)15 and 20 cm полученных значений. Для участка 2 наиболее интересен почвенный слой 10–20 см, так как он находится в рамках одного минерального суглинистого почвенного горизонта. Как видно, в техногенно-нарушенной криотурбированной почве температуропроводность растет в 2,5–3 раза по сравнению с фоновой почвой, за исключением тонкого верхнего органогенного слоя.

На основе полученных данных были проведены расчеты для восстановления усредненных коэффициентов температуропроводности для почвенных горизонтов на основе решения обратной задачи теплопроводности. Для участка 1, (2023 г.) была получена динамика коэффициентов температуропроводности для почвенного слоя 10–20 см на основе минимизации разницы температур расчетной и измеренной на глубине 15 см; для участков 1 и 2, (2024 г.) – для почвенного слоя 10–30 см на основе минимизации разницы температур на глубине 20 см (рис. 5). Наблюдаемая средняя разница расчетной и измеренной температур составляет 0,08 (участок 1, 2023 г.), 0,018 (участок 1, 2024 г.) и 0,04 0С (участок 2). Полученные данным методом средние значения температуропроводности представлены в табл. 3. Для участка 1 расчеты на основе многодневных измерений температуры, сделанные с годовым перерывом, показывают практически одинаковый результат. Для участка 2 в суглинистом горизонте наблюдается рост температуропроводности почти в 2,5 раза по сравнению с фоновой почвой, который согласуется с полученным ранее результатом. В целом можно отметить, что рассчитанные средние значения коэффициентов температуропроводности находятся в пределах значений, полученных на основе амплитудного и фазового методов (табл. 3).

Если рассматривать динамику изменений коэффициента температуропроводности (рис. 5), то для участка 1 изменения находятся в интервале 0,12–0,25∙10–6, а для 2–0,27–0,5∙10–6 м2/с. Наблюдаемые скачки коэффициентов связаны с достаточно резким изменением температуры, так, для участка 1 (2024 г.) на 15 и 30 сутки происходит заметное снижение амплитуд изменения температур на глубине 10 см (рис. 2), которое приводит к провалу численных значений температуропроводности. Исключение подобных значений изменит среднее значение коэффициента с 0,17 до 0,18∙10–6 м2/с.

Полученные расчетным методом средние коэффициенты температуропроводности для всех используемых методов в сравнении с данными полевых измерений по участку 1 имеют

Таблица. 3. Рассчитанные значения коэффициента температуропроводности

Table 3. The calculated values of thermal diffusivity

Амплитудный (2) и фазовый (3) методы
Участок, год	1, 2023	1, 2023	1, 2024	1, 2024	2, 2024	2, 2024
Почвенный слой	5–15 см	10–20 см	10–20 см	20–30 см	5–15 см	10–20 см
a∙106, м2/с (2)/(3)/ среднее	0,14/ 0,25/ 0,195	0,12/0,17/ 0,145	0,23/0,13/ 0,18	1,24/0,25 0,745	0,11/0,3/ 0,205	0,41/0,615/ 0,513
Решение обратной задачи теплопроводности
Участок, год	1, 2023		1, 2024		2, 2024
Почвенный слой	10–20 см		10–30 см		10–30 см
∙106, м2/с	0,17		0,17		0,39

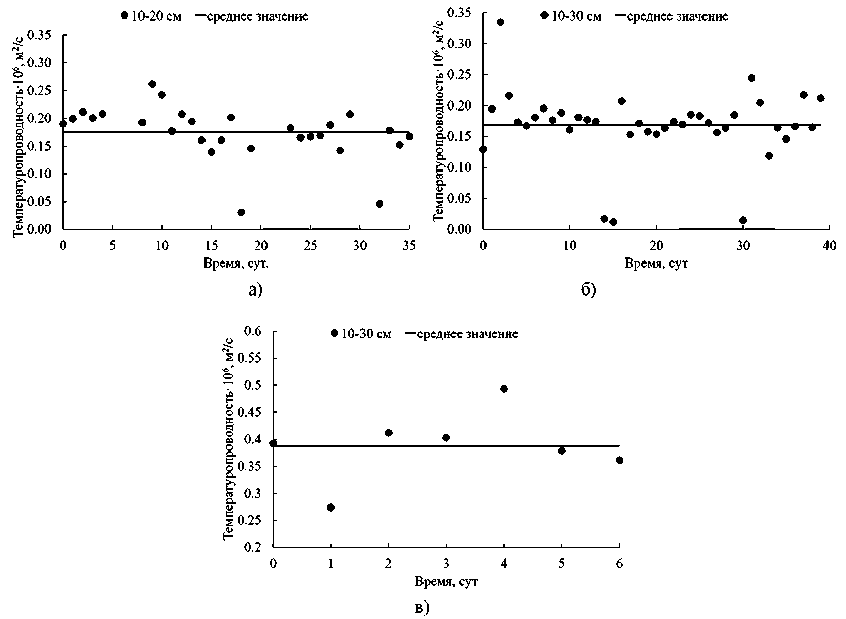
Рис. 5. Рассчитанные коэффициенты температуропроводности: а) для участка 1, 2023 г.; б) для участка 1, 2024 г.; в) для участка 2, 2024 г.

Fig. 5. The calculated values of thermal diffusivity: a) the test site 1, 2023; b) the test site 1, 2024; c) the test site 2, 2024

более высокие значения, до 35 % (исключая значения для 20–30 см, табл. 3). С учетом возможной погрешности измерений самим прибором в почвенном горизонте, имеющем высокую пористость, можно считать результаты достаточно близкими. Для участка 2 с более тяжелой и плотной почвой расчет методом, основанным на решении уравнения теплопроводности, практически совпадает с данными полевых измерений, а среднее значение на основе амплитудного и фазового методов показывает более высокие показатели, примерно на 25 %. Стоит также отметить, что при использовании методов (2) и (3) нельзя априори сказать, какой из них даёт более точный результат, поэтому необходимо использовать среднее значение.

Если рассматривать полученные результаты в совокупности, то для техногенно-трансформированной почвы (участок 2) температуропроводность выше более чем в два раза, чем для фоновой почвы (участок 1), что в итоге приводит к наблюдаемой разнице глубины растепления почв в 1,5–2 раза [16].

Заключение

Исследуемые почвы криолитозоны, распространенные в районе Норильского промышленного района, при техногенной трансформации могут претерпевать серьезные структурные изменения, которые приводят к изменению теплового режима и функционирования почв в це- лом. Это, в свою очередь, определяет такие важные характеристики для инфраструктурных объектов и биологических систем, как глубина растепления и скорость движения границы фазового перехода вода/лед.

На основании данных мониторинга температуры почвы показано, что в природных условиях показатели теплофизических свойств почв не остаются постоянными. В исследуемых почвах трансформация верхнего органогенного горизонта приводит к изменению коэффициента температуропроводности в 2,5–3 раза. Сравнение результатов прямых полевых измерений и обработки данных многодневной динамики температуры различных почвенных слоев демонстрирует в целом хорошее согласование. Но в случае использования амплитудного и фазового метода такое согласование наблюдается только при совместном осреднении значений, полученных обоими подходами, так как температурные колебания не являются идеальными гармоническими. Для третьего метода при расчете могут наблюдаться скачки коэффициента температуропроводности, возникающие при достаточно резком изменении температуры на верхней границе рассматриваемого слоя. Это говорит о том, что в данном случае модель не работает, и, возможно, в почве реализуются другие механизмы переноса тепла, отличные от теплопроводности.

Восстановленные коэффициенты температуропроводности на основе решения обратной задачи теплопроводности подтверждают предположение о сохранении высокого увлажнения почвы в течение летнего периода.

Представленные в статье результаты могут быть использованы при разработке моделей тепло- и влагопереноса, в том числе для нарушенных почв, расположенных в НПР.