Анализ термодинамических циклов низкотемпературных установок с учетом массопеременности хладагента

Теория, расчет и практика показали, что переход от циклов с постоянной массой агента к аналогичным циклам с переменной массой агента позволяет повысить эффективность энерго-хладоциклов от 20÷80 % в холодильной технике, в том числе тепловых насосов, до 40–100 % – в криогенной технике, теплоэнергетике, в том числе на АЭС, ТЭЦ. Это значит, что каждая 2-я и 3-я из станций могут быть законсервированы при повышении термического КПД работающих станций в 2–3 раза после их соответствующей модернизации по изложенному способу без существенных капитальных затрат. При этом решаются вопросы не только энергопотребления и энергосбережения в регионах, но и многие экологические проблемы [1].

Идея массопеременных (аддитивных, А -циклов) циклов, приближающихся по термодинамической эффективности к циклу Карно, была выдвинута в начале 1980-х гг. экс-президентом Международного института холода проф. Хазелденом [2–4]. Экспериментальная проверка цикла, аналогичная циклу Хазелдена, действительно показала его высокую эффективность. Термодинамический КПД обычной типовой холодильной машины, работающей в массопеременном, т. е. аддитивном, режиме возрастал на 20–30 %.

Такой эксперимент был поставлен в Московском институте химического машиностроения [5–6]. Высокая эффективность аддитивных циклов, используемых в различных областях техники, отмечалась и в других работах ученых [7–15].

Целью работы является получение зависимостей и разработка схем для создания и модернизации низкотемпературных установок с использованием массопеременности хладагента для повышения их эффективности и снижения эксплуатационных затрат на предприятиях пищевой промышленности.

Материалы и методы исследования

Для повышения эффективности термодинамических циклов применяли теоретические методы исследования и произвели испытания на одноступенчатой холодильной машине. Предлагаемый способ повышения эффективности существующих и вновь создаваемых машин относится к тем из них, которые работают по прямым – энергетическим ( Э ) и обратным – холодильным ( Х ) циклам. Эффективность первых, как известно, определяется термическим КПД, η (1), а вторых – холодильным коэффициентом, ε (2).

η =

ε =

Т- Т 0 _Т;

Т 0

Т- Т0 , где Т – высший температурный уровень агента в Э и Х циклах; Т0 – низший температурный уровень агента в Э и Х циклах.

Отсюда следует, что для заданных значений Т и Т 0 для 1 кг рабочего агента, величины η и ε всегда будут больше там, где средние за цикл величины температуры Т и разности температур Т и Т 0 будут для агента наименьшими. Для каждого конкретного Э и Х цикла этого можно добиться, перераспределив между температурами Т и Т 0 массу агента так, как показано в общем виде на рисунке 1 – для Э и Х циклов или на рисунке 2 – для Э цикла Ренкина.

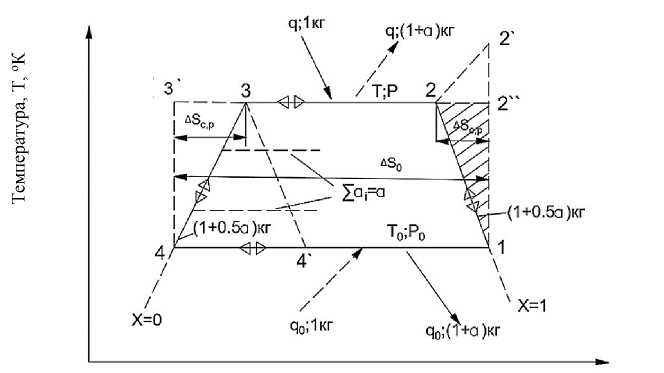
Энтропия, S, Дж/(кгК)

Х – степень сухости пара агента; α i – элементарные массы агента от процесса 3-4 к процессу 1-2; q, q 0 – удельные тепловые потоки на температурных уровнях Т и Т 0 для Э- (сплошные линии) и для Х- (пунктирные линии) циклов.

Рисунок 1 – Внутрицикловое перераспределение массы в цикле в координатах Т-S

Как видно из рисунка 1, обычный дроссельный Х -цикл 1–2'–3'–4' превращается при использовании А -фактора в цикл 1–2–3–4, где 1–2 процесс охлаждаемого сжатия агента по правой пограничной кривой ( Х =1), а процесс испарительного охлаждения агента 3–4 позволяет производить дросселирование агента без дроссельных потерь в т. 4. Графический и аналитический анализы неаддитивного ( НА ) Х -цикла Карно (1–2''–3'–4) позволяют сделать вывод, что их бесконечно большое количество по контуру (1–2–3–4) уменьшит в нем удельную работу сжатия с учетом А-фактора α на величину заштрихованной на рисунке 1 площади. Эта работа сжатия ( ℓ ) будет определяться по формуле (3):

ℓ=ℓ к ∙ (1–α ),

где 1 к - удельная работа в цикле Карно; ос - элементарная масса агента.

Удельная работа в цикле Карно определяется формулой (4):

ℓ к = ∆Т ∙ ∆S 0 .

Элементарная масса агента (а)определяется по формуле (5):

о = ^S/2^S o ,

где AS = AS с = AS р , если AS с ^ AS р , тогда AS = (AS_C + AS_p)/2.

мулой (6):

Величина холодильного коэффициента при этом для Х -цикла будет определяться фор-

_ ^ карно

1-а .

На рисунке 2 показана та же идея для осуществления аддитивного А-цикла Ренкина (процессы 1–2–3–4) вместо обычного неаддитивного (НА) – прототипа (процессы 1–2–3'–4). При этом получаемая в турбине в процессе 2–3 работа будет больше на величину заштрихованной площади (см. рис. 2) для А-варианта, так как расширяемый в турбине агент по сравнению с прототипом постоянно увеличивает свой средний располагаемый теплоперепад за счет дозировок потоками αi при промежуточной температуре Тi и промежуточном давлении Рi. Более того, в этом цикле по сравнению с прототипом имеется возможность для регенеративного теплообмена обратного потока агента после турбины с прямым потоком. Удельная величина регенеративной теплоты на рисунке 2 показана горизонтальной штриховкой. Аналогичная величина положительного воздействия А-фактора α на работу Э-цикла показана на этом рисунке косой штриховкой.

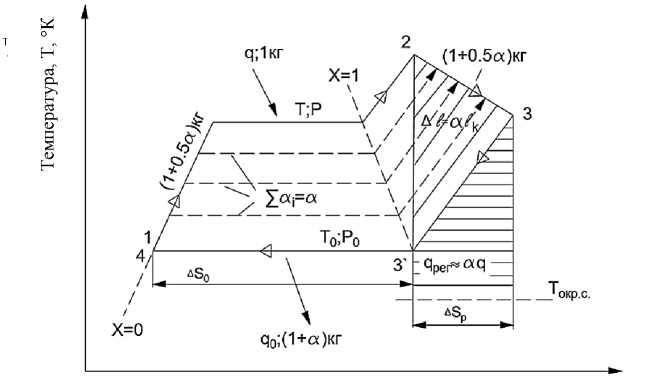
Энтропия, S, Дж/ (кг К)

Х – степень сухости пара агента; α i – элементарные массы агента; q, q 0 – удельные тепловые потоки на температурных уровнях Т и Т 0 для Э- (сплошные линии) и Х- (пунктирные линии) циклов.

Рисунок 2 – Внутрицикловое перераспределение массы в цикле Ренкина в координатах Т-S

С учетом этого величина термического КПД ( η ) для А -цикла будет определяться формулой (7):

_1+а

η = ηкарно     ,(7)

1-( где ηкарно – КПД цикла Карно; α – элементарная масса агента, определяется формулой (8).

α = ∆Т ∙ ∆Sр / 2ℓк ,(8)

где ∆Т = Т 2 – Т 0 , при ∆S р →∆S 0 для Э-циклов (см. рис. 2) и при ∆S→∆S 0 для Х-циклов.

Анализ циклов (см. рис. 2) показывает, что для КПД цикла ( η ) и холодильного коэффициента ( ε ) будут справедливы выражения (9) и (10) соответственно:

η = 3η карно.

ε = 2ε карно.

А -способ работы применим для хладо- и теплонасосной и крио- и теплонасосной техники (ХКТ), энерготехники на ТЭЦ, ТЭС, АЭС, ДВС, газотурбинных установок и др.

Проведем анализ цикла Хазелдена (1–2–3–4), суть которого показана на рисунке 3. Пар хладагента (ХА) сжимается в винтовом компрессоре (ВК) в состоянии, близком к сухому насыщению – кривая 1–2. Теплота сжатия при этом отводится от компрессора частично испаряющейся в нем жидкостью ХА, которая подается в ВК в зазор между его роторами и корпусом в дополнение к охлаждаемому и уплотняющему ВК маслу, но противотоком к сжимаемому в винтовом компрессоре пару ХА. Процесс испарительного охлаждения жидкого ХА в ВК – 3–4 идет по левой пограничной кривой (Х=0, где Х – степень сухости пара ХА). Процесс конденсации ХА – 2–3 идет при температуре Т, а процесс кипения – 4–1 – при температуре Т0. Таким образом, имеется реальная возможность осуществления обратного (0) холодильного цикла (1–2–3–4), эффективность которого так же легко оценить с помощью рисунка 3, как и прямого цикла (П). Анализ рисунка 3 показывает, что если отрезки пограничных кривых 1–2 и 3–4 аппроксимировать соответствующими пунктирными прямыми 1–2 и 3–4, то легко провести аналогию между А-циклом (1–2–3–4) и эквивалентным ему О-циклом Карно (1–2'–3'–4).

Действительно, геометрические пощади этих циклов под соответствующими отрезками 1–2 и 3–4 равны таким же треугольным площадкам над ними: 1–2'–2 и 3–3'–4. Это значит, что площади сравниваемых А -цикла и цикла Карно равны.

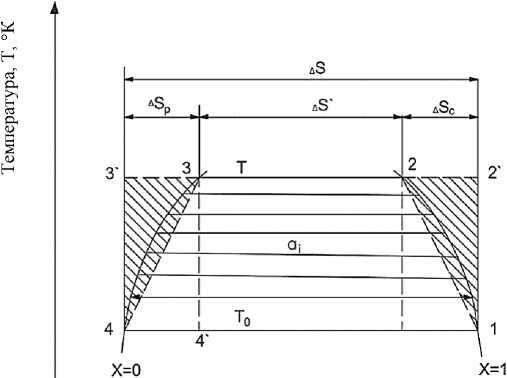
Энтропия, S, Дж/(кг К)

Рисунок 3 – Анализ цикла Хазелдена в координатах Т-S

Следовательно, их эффективности одинаковы. Термодинамический смысл площадок А -цикла под линиями 1–2 и 3–4 в координатах Т-S состоит в том, что они полностью соответствуют требуемой дополнительной холодопроизводительности в А -цикле для того, чтобы обеспечить охлаждение в этих процессах: от т. 1 до т. 2 при S ↓ и Т ↑ – при сжатии, от т. 3 до т. 4 при S ↓ и Т↓ – в процессе расширения или перед ним. Эти процессы кипения ХА в ВК на рисунке 3 показаны в виде горизонтальных векторов как потоки ( α i) пара, отводимого при испарении агента в процессе 3–4 к сжимаемому сухому пару в процессе 1–2.

Таким образом, из условия отношения рассматриваемых площадей А-цикла к площади этого же цикла можно получить соотношение для определения величины А-фактора (α), т. е. того дополнительного количества агента ∑αi (11), которое обеспечит холодом про- цессы 1–2 и 3–4:

ASC    Д5р a = уш = a + ap —— +—— = ^          р 2LS 2LS

№_c+ Д5 р

2LS '

где ^S_c, ^S p - изменение энтропии агента, соответственно в процессе 1-2 и 3-4 (рис. 3); AS – изменение энтропии агента в процессе 4–1; α с , α р – величина А -фактора, соответственно, для процесса 1–2 и 3–4.

Дополнительные площади диаграммы Т-S (см. рис. 3), эквивалентные α с и α р , представляющие собой добавочную работу, соответственно ℓ с и ℓ р , необходимую для работоспособности А -цикла 1–2–3–4, показаны на рисунке 3 штриховкой.

В соответствии с этим интенсивная составляющая удельной работы А -цикла будет равна (12):

ℓ и = ℓ карно ∙ (1-α) = ∆Т ∙ ∆S ∙ (1-α) = [q 0 ∙ (1-α)] / ε к ,             (12)

где ∆Т = Т – Т 0 – температурный диапазон работы; ∆S = ∆S' + ∆S с + ∆S р – энтропийный диапазон работы сравниваемых А -цикла и цикла Карно; q 0 = ∆i 1-4 = Т 0 ∙ ∆S – удельная массовая холодопроизводительность сравниваемых циклов, а ∆i 1-4 = i 1 - i 4 – разность энтальпий агента в соответствующих точках цикла; ε к = τ/(1-τ) – холодильный коэффициент идеального цикла Карно, τ = Т 0 /Т .

Удельная работа А -цикла с учетом аддитивной, т. е. экстенсивной, составляющей будет определяться выражением (13):

ℓ = ℓ к = ℓ и + αˑℓ к = q 0 /ε к = ℓ и + ℓ э ,                      (13)

где ℓ э – величина А -составляющей удельной работы или экстенсивная составляющая ее часть равна

ℓ э = αˑℓ к ,                                      (14)

где ℓ и – интенсивная составляющая удельной работы А -цикла.

Результаты исследования и их обсуждение

Возвращаясь к циклу Хазелдена (см. рис. 3) [3], видим, что этот цикл по эффективности не только сравним с циклом Карно, но и превосходит его, несмотря на наличие в нем двух необратимых процессов теплообмена 1–2 и 3–4. В данном случае это не противоречит законам термодинамики с учетом наличия в этих процессах теплообмена без потерь между прямыми и обратными потоками агента в цикле.

На основании изложенного на рисунке 3 следует, что внутри цикла 1–2–3–4 величины А -фактора α с и α р для соответствующих им процессов 1–2 и 3–4 изменяются от нуля в начале каждого из них (т. 1 и т. 3) до максимальной величины – в конце (т. 2 и т. 4), это означает, что средние для этих процессов и цикла в целом их величины можно принять равными 0,5 от максимальных. Следовательно, удельная работа А -цикла с учетом аддитивной составляющей будет определяться выражением (14), а интенсивная составляющая удельной работы А -цикла - выражением (16):

ℓ = ℓ и + 0,5ˑαˑℓ к = [q 0 ∙ (1-0,5ˑα)]/ε к = ℓ к ∙ (1-0,5ˑα).                (15)

ℓ э = -0,5α ∙ ℓ к .                                          (16)

Экстенсивная составляющая удельной работы А -цикла Хазелдена взята со знаком « - », так как площадь диаграммы этого цикла именно на эту величину получается меньше площади цикла Карно, эквивалентного ему. Эффективность А -цикла Хазелдена и аналогичных ему так называемых внутриаддитивных циклов ( ВА ) на основании вышеизложенных зависимостей будет определяться выражением (17):

ε ВА = ε к /(1–0,5ˑα).                                (17)

Для случаев, когда А -фактор обеспечивается внецикловыми потоками, отличными от внутрицикловых потоков α i , (см. рис. 3), цикл можно назвать циклом с внешней аддитивностью ( ВНА ).

В этом случае зависимости, аналогичные вышеприведенным, будут иметь вид (18) и (19):

ℓ ВНА = ℓ к ∙ (1-α) + α ∙ ℓ к = ℓ и + ℓ э ,                                  (18)

где ℓ ВНА – удельная работа для обратных ВНА -циклов.

ε ВНА = ε к ,                                             (19)

где ε ВНА – холодильный коэффициент для обратных ВНА -циклов.

Для обратных ( 0 ) циклов с А -фактором между процессами конденсации и кипения агента или между аналогичными им процессами охлаждения и нагревания при однофазных 0 -циклах холодильный коэффициент определяется выражением (20):

ε' ВА = ε к /(1-0,5ˑα'),                                  (20)

где α' = ∆Т'/2∆Т – величина А -фактора для процессов теплообмена; ∆Т' – максимальные изменения температур фазового перехода в фазовопереходном аппарате (испарителе или конденсаторе) или в фазовопостоянном, вызванные А -воздействием.

Простейший случай такого А -воздействия – это применение регулярного по всей длине аппарата дросселирования некоторого количества паровой фазы α' из конденсатора в испаритель, с тем чтобы в первом температура конденсации ступенчато понижалась, а во втором – ступенчато повышалась при элементном исполнении того и другого. Тогда, аппроксимируя эти ступенчатые линии некоторой прямой, можно говорить о температуропеременных процессах фазового перехода для чистых или азеотропных агентов.

При полном А -воздействии в обратных ( 0 ) циклах на все их процессы в соответствии с (16) и (19) справедливо выражение (20), а холодильный коэффициент будет определяться выражением (21):

ε' ВА < ε ПА > ε ВА .                                    (21)

ε ПА = ε к /(1-0,5ˑα-0,5ˑα').                            (22)

Зависимости (21) и (22) справедливы также при внутрицикловом воздействии на агент, для этого случая, т. е. для ВНА -цикла, ε ПА будет равна ε к .

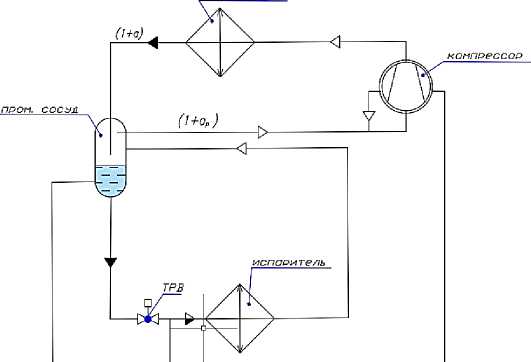
На рисунке 4 представлены реальные схемы (варианты) модернизации одноступенчатых холодильных систем, использующих принцип аддитивности. Произведены предварительные испытания по схемам а - в (рис. 4) на хладагентах R404, R410 и R600a, которые показали повышение холодопроизводительности и повышение коэффициента холодильной мощности на 25–30 %.

конд еноа тор

-4--[хмМх—^

а

Рисунок 4 – Схемы модернизации одноступенчатых холодильных систем: а - схема с промежуточным сосудом, с регулированием расхода хладагента и охлаждением компрессора

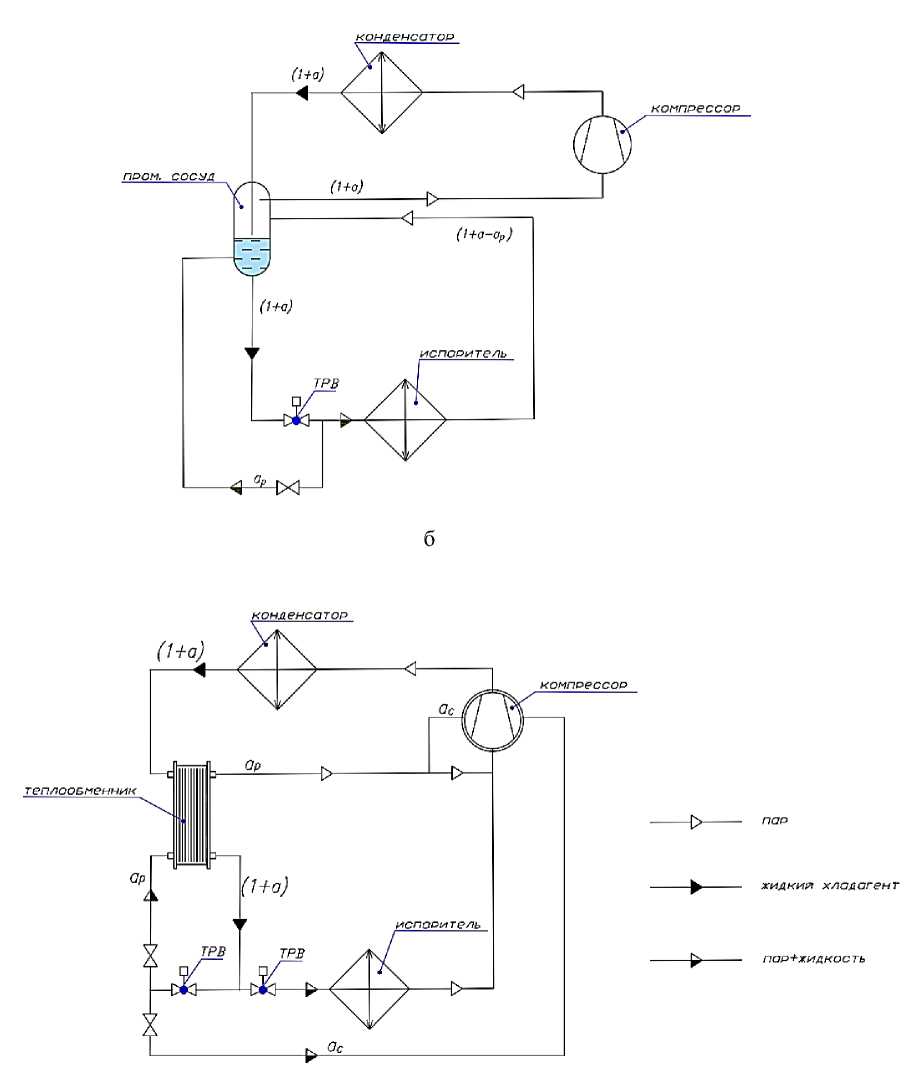
в

Рисунок 4 (продолжение) – Схемы модернизации одноступенчатых холодильных систем: б - схема с промежуточным сосудом, с регулированием расхода хладагента; в - схема с теплообменником-переохладителем и с охлаждением компрессора

Планируется произвести широкое комплексное исследование с использованием факторного анализа на природных, углеводородных хладагентах и на синтетических хладагентах, которые не разрушают озоновый слой земли и не оказывают влияние на глобальное потепление, с целью выдачи практических рекомендаций для модернизации существующих установок и при установке новых.

Заключение

Полученные зависимости и схемы холодильных циклов с использованием массопере-менности хладагента является основой для практического усовершенствования холодильных и теплоэнергетических установок предприятий пищевой промышленности с целью повышения эффективности этих установок и снижения эксплуатационных затрат.

Реальные схемы систем холодоснабжения, представленные на рисунке 4, позволяют согласно предварительным испытаниям повысить холодопроизводительность путем переохлаждения, а также увеличить холодильный коэффициент на 25–30 % в том числе и за счет использования процесса сжатия в компрессоре с отводом теплоты;