Аналог уравнения Эйлера и необходимые условия оптимальности второго порядка в одной задаче оптимального управления с переменной структурой

Среди множества задач оптимального управления особое место занимают задачи оптимального управления многоэтапными процессами, так называемые задачи оптимального управления системами с переменной структурой (напр. [1–7]). Ряд задач оптимального управления, описываемых на различных отрезках времени, изучен в работах [1–7].

В статье ставится и рассматривается задача оптимального управления, описываемая совокупностью дифференциальных и интегральных (типа Вольтерра) уравнений. Доказано необходимое условие оптимальности первого порядка в форме уравнения Эйлера. Затем получены необходимые условия оптимальности второго порядка для классических экстремалей и изучен случай вырождения аналога, условия Лежандра — Клебша.

1 Постановка задачи

Допустим, что управляемый непрерывный процесс на фиксированном отрезке времени T = T 1 и T 2 ( T 1 = [ t 0 , t 1 ] , T 2 = [ t 1 , t 2 ] ) описывается совокупностью обыкновенных дифференциальных и интегральных (типа Воль-терра) уравнений вида:

x = f (t, x, u), t e T, x (tо ) = xo,                                              (1)

t

У ^{( t ) =} f g ^{( t}, s, У ⁽ s ) , v ⁽ s )) ^ds + ^{G (} x ^{( t} 1 )) , t ^{G T} 2 ,                   ⁽²⁾

t ₁

Здесь f (t, x, u) (g(t, s, y, v)) — заданная n (m) -мерная вектор-функция, непрерывная по совокупности переменных вместе с частными производными по (x, u)((y, v)) до второго порядка включительно, 10,11,12 (t0 < t1 < 12) — заданы, x0 — заданный постоянный вектор, G(x) — заданная m -мерная дважды непрерывно дифференцируемая вектор-функция, u (t) (v(t)) — r (q) -мерный кусочно-непрерывный (с конечным числом точек разрыва первого рода) вектор управляющих воздействий со значениями из заданного непустого, ограниченного и открытого множества U (V), т. е.

u ( t ) e U c R^r , t e T , v ( t ) e V c R q , t e T ₂ .

Пару ^{( u} o^{( t} ) ^v o ^{( t} ) )

, удовлетворяющую вышеприведенным условиям, на- зовем допустимым управлением.

Под решением системы (1), (2), соответствующим допустимому управлению (uo (t),vo (t)), понимается пара (xo(t),yo(t)), удовлетворяющая соотношениям (1), (2), где xo (t) — непрерывная и кусочно-гладкая век тор-функция, а yo (t) — непрерывная вектор-функция.

Предполагается, что каждому допустимому управлению соответствует единственное решение системы (1), (2). Рассмотрим задачу о минимуме функционала

I (u,v) = Фх (x (t1 )) + Ф2 (У (t2 ))

( " • ( t ) , V ( t ) )

при ограничениях (1)–(3).

Здесь Ф1 (x), ф2 (y) — заданные дважды непрерывно дифференцируе- мые скалярные функции.

Допустимое управление, доставляющее минимум функционалу (4) при ограничениях (1)–(3), назовем оптимальным управлением, а соответст- вующий процесс (uo (t),vo (t),xo(t),yo (t))

— оптимальным процессом.

2 Формула для приращения функционала

Пусть ( u ^o ( t ), v ^o ( t ), x ^o ( t ), y ^o ( t ) ) — фиксированный допустимый процесс.

Через

( u ( t ) = u ^o ( t ) + A u ( t ) , v ( t ) = v ^o ( t ) + A v ( t ) , x ( t ) = x ^o ( t ) + A x ( t ) , y ( t ) = y ^o ( t ) + A y ( t ) ) обозначим произвольный допустимый процесс и запишем приращение функционала качества

AI (uo ,vo ) = I (u,v)-1 (uo ,vo ) =

= [^1 (x (t1 ))- Ф1 (xo (t1 ))] + [^2 (y (t2 )) - Ф2 (yo (t2 ))] .

Далее ясно, что ( A x ( t ), A y ( t )) является решением задачи

A x ( t ) = f ( t , x ( t ) , u ( t )) - f ( t , x ^o ( t ), u ^o ( t ) ) ,

A x ( t о ) = 0,

t

Ay (t) = J[g (t, s, y(s),v(s))- g (t,s, yo (s), vo (s))]ds + t1                                                                               (8)

+G(x (ti))- G(xo (11)).

Предположим, что у ⁰( t ), p ^o ( t ) — пока произвольные n и m -мерные соответственно вектор-функции.

При этом из (6) и (8) получаем справедливость тождеств t1                                                           ti

Jv° (t) Ax (t) dt = Jyo (t)[f (t,x (t),u (t))-f (t,xo (t), uo (t))]dt, (9)

t ₀ t ₀

Jpo (t) Ay (t) dt = Jpo (t)[G(x(t1))-G(xo (11))]dt +

⁺J p ^o ( t ) k g ( t , s , y ( s ) , v ( s ) ) - g ( t , s , y ^o ( s ) , t ,               L t 1

v ^o ( s ) ) ] ds dt .

Учитывая тождества (9), (10), приращение (5) функционала (4) запишем в виде

AI (uo ,vo ) = [Pi (x ( t, ))- ф, (xo (ti ))] + [^2 (y (t2 ))- фг (yo (t2 ))] + ti

+y ^o ( t , ) A x ( 1 1 ) - Jt/& ^o ( t ) A x ( t ) dt -                       (11)

t ₀

t 1                                                                                                                                    t 2

-Jyo (t)[ f (t,x (t),u (t))- f (t,xo (t), uo (t))] dt + Jpo (t)Ay(t)dt - t0t1

t 2               ,

_ ° ( 5 ) ) ] d5

dt —

-J Jp° (5)[g(5,t,У (5),v (5))-g(5,t,У° (5), tiL i

• — j p ° ( t ) [ G ( x ( t , ) ) — G ( x ° ( t , ) ) ] dt.

t ₁

Полагая

N ⁽ P °^{( t} ) , ^x ) = P ° ' ^{( t} ) G ^{( x} )

и используя формулу Тейлора, формулу приращения (11) запишем в виде

, х d^'(x° (ti))           1         dV(x° (ti))

A1 (u°,№) =----' Ax(ti) + -Ax'(ti)-----' Ax(ti) + ax            2          ax

+j Ф2 ( У (2 )) ^g (12, t, - (t) , _( t ))-g ( t 2, t, yO ( t ), v° ( t ))] dt + ° (||Ax ( ti )||2 ) + 'y

• 1.    , ( / 2^2 (У° ( t 2 )). , X 1 t2.      x52 N (p° (t ), x° ( ti ))

+ TAУ ( t2 )---------- AУ ( t 2 )-H^ ( ti )---------------Ax ( t 1 ) +

2             d y               2 t               d x

+ O 2

t 1                                                                                                            -1

(||AУ ( t2 )ll)+ v°' (t)—j Gx (x° ( ti )) po (t)dt Ax ( ti ) —jV ° (t )Ax (t)dt

t i

t 0

t i

t 0

t i                                                                                                                                  t 2

—Jv° (t)[f (t,x(t),u (t)) — f (t,x° (t), u° (t))]dt + Jp° (t)AУ(t)dt — t 0                                                                                                                                 ti

5, t, ti  _?1

У ( t ) , v ( t ) ) ^— g ( ⁵ , t , У ° ( t ) , v ° ( t ) ) ] d⁵

dt

—

,j ° 3 ( t ,| ^{A (} t 1 )||² ) t i

dt .

Здесь o ( a ² ) величина более высокого порядка чем а ², т. е. o ( a ² )/ а ² ^ 0 при а ^ 0.

Введя аналоги функций Гамильтона — Понтрягина посредством формул

H ( t , x , u , v ° ) = V °' f ( t , x , u ) ,

M ( t , У , v , P ° ) =

5^2 (У° (12))

------------g(t2,t,У,v) + JP° (5)g(t,5,У,v)d5 , ауt формулу приращения (12) запишем в виде:

ti Г“I

AI(u° ,v° ) = -j[H(t, x (t), u (t), v° (t)) — H(t, x° (t), u° (t), v° (t))] dt + t0

1. ,, ₄^d2 p ' ( x ^o ( t i ) )             i           a ² p 2 ( y ^o ( t ₂ ) )

⁺ 2 ^{A x (} t i)— a X²— ^{Ax (} t 1 ⁾⁺ 2 ^A y ⁽ t 2)—"^A y ⁽ t 2 ^)—

— J [ M ( t , y ( t ) , v ( t ) , P ^o ( t ) ) — M ( t , y o ( t ) , v ^o ( t ) , P ^o ( t ) ) ] dt + t ₁

+ ¹ | A x ^^ N^t l^

t ₁

. V ( t i ) + ^{d p} i ^{( x} o ⁽ t i ) ) a x

A x ( t i ) +

‘

—

J ^( У ( ti )) Po ( t ) dt Ax ( ti ) — ti

t 2

—Jpo (t)Ay(t)dt + oi t1

t ₂

t ₁

Предположим, что ( v o ( t ) , p ^o ( t ) ) является решением системы уравнений V ^o ( t ) = — H ( t , x ^o ( t ) , u ^o ( t V ( t ) ) ,

vo (ti) =—dPi M t1))+J gx (xo (ti)) po (t) dt, po (t ) = My (t, yo (t), vo (t), po (t)).

Тогда формула приращения (13) может быть представлена в виде:

A l ( u ^o ,v ^o ) =                                  (i4)

t ₁

t ₂

= — J H_M '( t , x ^o ( t ) , u ^o ( t ) , v o ( t ) ) A u ( t ) dt — J M V ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) A v ( t ) dt — t ₀ t ₁

^— ! J [^{A x} '( t ) H xx ( t , ^x o ( t ) , u o ( t ) , ^ o ( t ) ) ^{A x} ( t ) ^{+ 2 A u} '( t ) H ux ( t , ^x o ( t ) , ^u o ( t ) , ^ o ( t ) ) ^{A x (} t ) ⁺ 2 _{t 0}

+A u ' ( t ) H uu ( t , x ^o ( t ) , u ^o ( t ) , V o ( t ) ) A u ( t ) ] dt — ! ^[ [A y ‘ ( t ) M yy ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) A y(t ) + 2 _{t 1}

+ 2 A V ( t ) M vy ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) A y ^{( t} ) + . i „ d² P i ( x ^o ( t i ))    , , ^+A v ( t ) M vv ( t , y ( t ) , ^v ( t ) , p ( t ) ) ^{A v} ( t ) ] ^dt + 2 ^{A x} ( t i )—d x ^—”^{A x} ( t i ) ⁺

⁺ 2 ^A y ' ( t 2 )    P 2 ⁽ y 2 ^{( 2} ) ) ^A y ( t 2 ) ^— P3 ( t , |^{A x} ( t i )||² ) ^{dt +}

^{2                d y}                   t i

^{+ o} i ^{( A ( t} i )| ^{2 ) + o} 2 ^{( A} y ^{( t} 2 ) |^{2 ) —} 2 ^{A x}' ^{( t} i ^{) 5} N ⁽ P d _x 2^{X ( t i} ) ) ^{A x ( t} i ) .

3 Оценка нормы приращения состояния

Из тождеств (6)–(8), используя условие Липшица, получим t

IlAx(t) - L jiiAx(^)+iiAu(sяds,                        (15)

t0

t

||AУ (t) - L 2 j[AУ(т ) +1|A v(т Я dT + L з| |Ax (t 1 )|,                  (16)

t ₀

где L i = const >  0, i = 1,3 — некоторые постоянные.

Применяя к неравенствам (15), (16) обобщенную лемму Гронуолла — Беллмана, (напр. [8]) получим справедливость оценок

t

IIAx(t)- L4 jl!Au(sJIds ,                                   (17)

t ₀

||^A У ^{( t ) - L} 5

t

j||A v (s )| ds +||Ax(t 1 )| t1

где L i = const >  0, i = 4,5 — некоторые постоянные.

Из (18) с учетом (17) следует, что

II^A У ^{( t ) - L} 6

tt

J||A v (s ) ds + J||A u (s )| ds t1                                     t0

L, = const >  0 .

4 Вариации функционала (4) и уравнения в вариациях

Из (6)-(8) получаем, что приращение ( A x ( t ), A y ( t )) траектории

( x ^o ( t ) , y ^o ( t ) ) является решением следующей линеаризованной системы

Ax (t)=fx (t, xo (t), uo (t ))Ax (t)+fu (t, xo (t), uo (t ))a u (t)+odi^ (t )i+iiA u (t )i), (20)

A x ( t 0 ) = 0,

AУ(t) = j[gy (t,s,yo (s), vo (s))Ay (s) + gv (t,s,yo (s), vo (s))Av(s) + t1                                                                                   (22)

+o(||Ay ( s )|| + ||Av (s )||)] ds + Gx (xo (t, ))Ax (t,) + о (||Ax ( t, )||).

В силу открытости множеств U и V

( u ^o ( t ), v ^o ( t ) ) можно определить по формуле

AuE (t ) = s5u (t), t e T1,

AvE (t) = e 8v (t), t e T2.

специальное приращение

Здесь 5 u ( t ) e R^r , t e T , 8 v(t ) e R^q , t e T ₂ — произвольные кусочнонепрерывные (с конечным числом точек разрыва первого рода) ограниченные вектор-функции, а £ — произвольное, достаточно малое по абсолютной величине число.

Допустим, что ( A x , ( t ) , A y , ( t )) специальное приращение траектории ( х ^о ( t ) , y ^o ( t ) ) , соответствующее приращению ( u ^o ( t ), v ^o ( t ) ) .

Из (20)–(21) ясно, что

Ax, (t) = J [fX (s,xo (s), uo (s))Ax, (s) + fU (s,xo (s), uo (s))Au (s) + t0

+o(||Ax (s )|| + ||A u (s )||)] ds,

Ay, (s) = J [gy (t,s,yo (s), vo (s))Ay, (s) + gv (t,s,yo (s), vo (s))Av, (s) + +o(|Ay, (s )|| + ||A v, (s )||)] ds + Gx (xo (,,))Ax, (t,) + o(||Ax, (t,)||).

Теперь ( A x , ( t ) , A y , ( t )) будем искать в виде:

Ax, (t) = ,Sx (t) + o(,; t),

Ay,(t) = ,Sy (t) + o (.; t), где (Sx(t),Sy(t)) — пока неизвестная (n + m) -мерная вектор-функция.

Принимая во внимание оценки (17) и (19) в (24)–(25), докажем, что в разложении (26) ( S x ( t ), S y ( t )) является решением следующего уравнения в вариациях:

S x ( t ) = f x ( t, X ^o ( t ), u ^o ( t ) ) S x ( t ) + f ( t, x ^o ( t ), u ^o ( t ) ) S u ( t ) ,

S x ( t о ) = 0,

Sy (t) = J [gy (t, s,yo (s), vo (s))Sy (s) + gv (t,s,yo (s), vo (s))Sv (s)]ds + t1

+Gx (xo (t,)) Sx (t,).

Учитывая (23), оценки (17), (19) и разложения (26) в формуле приращения (14), приходим к разложению

AI, (uo ,vo) = I (uo + Au, ,vo + Av,)-1 (u o,vo ) =

= -,

t ₁ t ₂

J Hu( t, xo (t), uo (t), vo (t)) Su (t) dt + f Mv( t, yo (t), vo (t), po (t ))Sv (t) dt t0t1

, ²     I,)⁵² ” ! ^{x (} t ¹ ) ).?              1⁸² ^ ^{2 (} y ⁽ t ² )Li

+T f(ti)   ax2   Sx(ti)+Sy (t1 )^— Sy(t2)

-

—5 x '( t , )

-2 S N (po (t), xo (t,)) d

5 x ( t , ) -

^J         dx²

^- 1

^t 1

—J[ax‘(t)Hxx (t,xo (t), uo (t), V (-))5x(t) + 25u‘(t)Hux (t,xo (t), uo (t), V (t))5x(t) + t0

+5u'(t)Hu (t,x (t), uo (t), V (t))au(t)]d—J^t)Myy (t,yo (t), vo (t), po (t))ay(t)+ +2aV(t)M,(t,yo(t), vo(t),po(t))ay(t) +

+av(t)Mvv(t,yo (t), vo (t), po (t))5v(t)]dt}+o(s2).                    (30)

Из разложения (30) ясно, что первая и вторая вариации (в классическом смысле (напр. [9; 10])) функционала критерия качества (4) имеют соответственно вид:

—/

5 ¹ I ( u ^o ,

v ^o ; 5 u , 5 v ) = — J h „ '( t , x ^o ( t ) , u ^o ( t ) , V ^o ( t ) ) 5 u ( t ) dt + L

^{1 2}                                                      X

⁺J M V ( ^t , y ^o ( ^t ) , v ^o ( ^t ) , p ^o ( ^t ) ) ^a v ( ^t ) ^dt , t 1                                                                   J

a2I(uo ,vo; 5u,av) = d2® (xo (t,))                  d2^ (yo (t2))

=ax(t,)^3^1225x(11)+ay(12) ф2 2(2)) ay (12 )— оx                        оy

. vaГ'2:N(p(t)■ xo(t,)) 5x ( -1 ) J

a x ²

dx ax(t, )—|Гах'(t)Hxx (t,xo (t), uo (t), vo (t))ax(t) t

+2au(t)Hux (t,xo (t), uo (t), v (t))ax(t)+au(t)Huu (t,xo (t), uo (t), v (t))au(t)]dt+ a2®,(yo(t2))           12r

+ay (12)—. 2     5у (12 )—J[ay' (t) Myy (t, yo (t), vo (t), po (t ))ay (t)+

O y

+25v'(t)Mvy (t,yo (t), vo (t), po (t))ay(t)+ av'(t)Mvv (t,yo (t), vo (t), po (t))av(t)]dt.

Запишем интегральное представление решения ( 5 x , 5 у ) уравнения в вариациях. Решение линейной задачи Коши (27), (28) допускает представление (напр. [9; 11])

a x ( t ) = J f ( t, т ) / u ( т ,x ^o ( т ) , u ^o ( т ) ) a u ( т ) d T ,          (33)

где F ( ‘, т ) ( n х n ) — матрица Коши, являющаяся решением задачи

F T ^{( t , T} ) = - F ⁽ ‘ ^{, T} ) Jx ^{( т} , У ^{О ( т} ) v ^{O ( т} ) ) , F ⁽ ‘ , ‘ ) = ^E 1 ,

( E₁ - ( n х n ) единичная матрица).

Решение S y ( t ) линейного неоднородного интегрального уравнения (29) допускает представление [12-14]

t

S У (‘ ) = J R (‘,T)

‘ 1

T

Jgv (T,s,yo (s), vo (s))Sv(s)ds + Gx (xo (‘ 1 ))Sx (‘ 1)

‘ 1

t

+J gv ( ‘,T, УО (T ), vo (T )) Sv (T ) dT + Gx ( xo ( ‘ 1 )) Sx ( ‘ 1 ), t1

dT +

где R ( t , s ) — ( m х m ) -матричная функция (резольвента), которая удовле-

творяет матричным интегральным уравнениям

t

R(‘,T) = JR(‘,s)gx (s,T,yo (T), vo (T))ds + gy (‘,T,yo (T)

T

vo

(t )),

t

R(t,t) = Jgy (s,t,yo (t), vo (t))R(s,t)ds + gz (t,t,yo (t), vo (t)).

T

Из (34), используя формулу Дирихле (напр. [9]), будем иметь

tt

Sy(‘)=J JR (‘,s)gv (s,T,yo (T) t1 L t

vo (t )) ds

S v (t ) d T +

+J R (t,t ) Gx (xo (t1)) Sx (t1) dT +

‘ 1

t

+Jgv (‘,T, yo (T) , vo (T))Sv (T)dT + Gx (xo (t 1 ))Sx (t 1 ).

t 1

Следовательно,

^y(t)=J JR(t,s)gv(s,T,yo (T), vo (T))ds+gv (t,T,yo (T), vo (T)) t1 L t

t

J R(t,t)Gx (xo (t1))dT + Gx (xo (t1))

. t 1

Принимая во внимание (33), в (35) получим

tt

S x ( t ₁ ) .

S v ( t ) d T +

Sy (t) = J JR(t,s)gv (s,T,yo (t), vo (t))ds + gv (t,T,yo (t), vo (t)) Sv(t)dT +

t1 L t

+J J R(t,t)Gx (xo (‘1))dT + Gx (xo (11))

‘ о L ‘ 1

F ( ‘ 1 , s ) f u. ( s , x ^o ( s ) , u ^o ( s ) ) S u ( s ) ds .(36)

Положим

t

Q , ( t^{, T} ) = f R ( t , s ) g v ( s ^{, T} , y ^o ( ^T ) , v ^o ( ^T ) ) ds + g v ( t ^{, T} , y ^o ( ^T ) , v o ( ^T ) ) ,

T

^Q 2 ( t , s ) =

t f R (t,t) Gx (xo (t,))dT + Gx (xo (t,))

t 1

^F ( t 2 , s ) fu ( s , xo ( s ) ,

uo

⁽ s ) ) .

Тогда формула представления (36) записывается в виде tt

5y(t) = f Q, (t,t) 5v(t)dT + f Q2 (t,s) 5u(s) ds.(37)

t1

Из первых вариаций (31) и (32) функционала качества в силу извест

ных результатов классического вариационного исчисления следует, что вдоль оптимального процесса ( u ^o ( t ) , v ^o ( t ) , x ^o ( t ) , y ^o ( t ) ) выполняются

соотношения

t i                                                                                             t 2

f H ‘ ( t , x ^o ( t ) , u ^o ( t ) , V ( t ) ) 5 u ( t ) dt + f M' _v ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) 5 v ( t ) dt = 0,(38)

t о                                                                                             t i

5 x '( t _i )

^d ® ( ^x ( t i ) ) a x²

, _{x ( x} a² ® , ( y ^o ( 1 ₂)) _{( x} ^{5 x} ( t i ) + ⁵ y ' ( t 2 )   2 ⁵ У ( t 2 ) -d y

- 5 x '( t _i )

■- - S N ( p o ( t ) , x o ( t , ) )

f      ax ti

t i

5 x ( t _i ) - f |^ 5 x '( t ) H xx ( t , x ^o ( t ) , u ^o ( t ) , v o ( t ) ) 5 x ( t ) + t o

+ 2 5 u '( t ) H ux ( t , x ^o ( t ) , u ^o ( t ) , V ( t ) ) 5 x ( t ) + 5 u '( t ) H uu ( t , x ^o ( t ) , u ^o ( t ) , ^ ° ( t ) ) 5 u ( t ) ] dt -

^- f [ ⁵ y ' ( t ) M yy ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) ⁵ У ( t ) ^{+ 2 5 v} '( t ) M y ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) ⁵ y ( t ) t i

+ 5 v ‘ ( t ) M vv ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) 5 v ( t ) ] dt > 0.                     (39)

Соотношения (38), (39) являются неявными необходимыми условиями

оптимальности первого и второго порядка соответственно.

Из (38), применяя схему, например из [i0], получим

H u ( e , x ^o ( 0 ) , u ^o ( 0 ) , v ^o ( 0 ) ) = 0, для всех 0 е [ t ₀ , t _t ) ,             (40)

M v ( 5 , y ^o ( £ ) , v ^o ( ^ ), p ^o ( ^ ) ) = 0, для всех ^ е [ x 0 , x , ) .           (4i)

Здесь и в дальнейшем через 0 е [ t ₀ , t , ) ( ^ e [ t _t , 1 ₂ )) обозначена произ

вольная точка непрерывности допустимого управления u ^o

( t ) (v ( t ) ) .

Пара соотношений (40), (41) есть аналог уравнения Эйлера [9; 10] для рассматриваемой задачи.

Каждое допустимое управление ( u ^o ( t ) , v ^o ( t ) ) , удовлетворяющее

уравнению Эйлера (40), (41), назовем классической экстремалью.

С помощью неравенства (39) удается получить необходимые условия оптимальности второго порядка, носящие конструктивный характер. Полагая в неравенстве (39) Su(t)^ 0 и Sv(t) = 0, получаем, что вдоль класси- ческой оптимальной экстремали

2—^ 5х (ti) + Sy '(t2)----—2—Sy ( t2 ) -

-Sx'( ti)

t ² a ² n ( p o ( t ) , x o ( t i ) )

^J         a x²

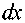
Sx (ti)-

t ₁

-J[Sx'(t)Hxx (t,xo (t), uo (t), y° (t))Sx(t)+2Su'(t)Hux (t,xo (t), uo (t), y° (t))Sx(t) + t0

+Su*(t)H,u (t,xo (t), uo (t), v° (t))Su(t)Jdt - t2

• - J S y ' ( t ) M ( t , y ^o ( t ) , v ^o ( t ) , p ^o ( t ) ) S y ( t ) dt >  0.                (42)

t ₁

При этом решение уравнения в вариациях (27) принимает вид t1

S y ( t ) = J Q₂ ( t , s ) S u ( s ) ds .                        (43)

t ₀

Используя представление (33) и (43) займемся преобразованием отдельных слагаемых в неравенстве (42).

Имеем a2^ (x° (t, Sx'(ti) Ф1 ( 2( 1))Sx(ti) = ax t1 t1      , _ < , x                          x d2rn (xo (t,))

= JJSu'(^)/u'(r,xo (t), uo (t))F(ti,T)-----—2-----x

dx xF(ti,s) fu (s,xo (s), uo (s))Su(s)dsdT

Sx '(t_)[ t2 d2N(p:(t),x:(^ dt 1 Sx (tx)= L.        dx           J t1t

= JJ ^{S u} ' ( t ) ^f ‘(r, x ^o (t )

t ₀ t

^u ° ( ^T ) ) F ' ( t r ^r )

-i 52 N (po (t), xo (t)) dt j         ax t0

xF(ti,s)fu (s,xo (s), uo (s))Su(s)dsdT, t1

J5u'(t)Hux (t,x- (t), u- (t), V- (t))5x(t)dt = t0

t Г t                                                         1

=J jS u ' ( т ) H ( т , x ^- ( т ) , u ^- ( т ) , v ^- ( т ) ) 5 x ( t ) dt f ( t , x ^- ( t ) , u ^- ( t ) ) 5 u ( t ) dt ,

$ Lt                                                 J

J5x'(t)Hxx(t,x-(t), u-(t), V(t))5x(t)dt =JJ5и(т)/и'(т,x-(т), u-(т))x

t ₀

t ₁

tt ₀

j F ( t, т ) H xx ( т , x ^- ( т ) , u ^- ( т ) , ^ ( т ) ) F ( t , s ) dt f_u ( s,x ^- ( s ) , u ^- ( s ) ) 5 u ( s ) dsd тах ( т , s )

т ,

J5y‘(t)Myy (t,y- (t), v- (t), p- (t))5y (t)dt = t1

^t 1 ¹ 1                          ¹ 2

= jj 5U '(т ) J ^ t ,т ) Myy ( t , УО ( t ) , VO ( t ), PO ( t )) Q2 ( t , s ) dt t oto                L ti

5 У ‘(12 )

52^2 (yo (12 )) dy2

5 У (12 ) =

5 u ( s ) dsd т ,

t ₁ t ₁

jj ^{5 u , ( т} ) Q 2 ^{( 1} 2 ^{, т} )

t ₀ t ₀

5 2 ^ 2 ( У ^О ( ¹ 2 ) ) d y²

Q ₂( 1 ₂, s ) 5 u ( s ) dsd т

Введя обозначение

K(т,s) = -Л'(т,xo (т), uo (т))

F ‘(11,т)

5 ^2< P i ( ^x o ( ^t i ) ) d x²

F (11,s)

t ₁

+ J   F‘(t1,т)Hxx (t,xo (t), uo (t), vo (t))F(11,s)dt - тах(т, s)

—F ‘(t1,т)

- Q2(12,т )

t ₂

J t1

a - N ( p o ( t ) , x - ( 1 1 ) ) d_t

5 ² ^ 2 ( У ^- ( ¹ 2 ) ) d y²

^Q 2 ( ¹ 2 , s )

F (t1,s )-

^f u ( s , x o ( s ) , ^U o ( s ) ) ,

и учитывая тождества (44)–(49) в неравенстве (42), получим

t ₁ t ₁

+ JJ S u ' ( т ) K ( т , s ) S u ( s ) dsd т + t ₀ t ₀

+2J

t ₀

t ₁

J S u ' ( т )

t

d2H(t, x (t), uo (t), -/ (t))

d u d x

F ( т ,t ) dt f_u ( t , x ^o ( t ) , u ^o ( t ) ) S u ( t ) dt + (51)

t ₁

+ J S u ‘ ( t ) H_uu ( t , x o ( t ) , u ^o ( t ) , ^ ° ( t ) ) S u ( t ) dt <  0. t ₀

Теперь предположим, что S u ( t ) = 0, S v ( t ) ф 0. Тогда из представлений (33), (37) следует, что S x ( t ) = 0, а

S У ( t ) = J Q i ( t , т ) S v ( т ) d т .                          (52)

t ₁

При этом неравенство (39) примет вид

д^ (yo (t,))          2Г

Sy ‘(12)    2^2     ’ Sy (12 )-J[Sy ‘(t) M. (t, yo (t), vo (t), po (t)) Sy (t)+ (53)

^{c y}

+2Sv'(t) Mvy ( t, yo (t), vo (t ), po (t )) SУ (t ) +

+ 2Sv‘(t)M (t, yo (t), vo (t), po (t))Sv (t)> 0.

Используя представление (52), убеждаемся в справедливости тождеств

, x d'^. (yo (12))    , x t2t2                  d'^. (yo (12))Sy'( t2 )---------- Sy ( t2 ) = J JSv'(t) Q?i'(t2,т )----------- QI ( t2, s )Sv(s ) dsdт, (54)

a y              tt                 c y

J Sv‘(t)Mvy (t, yo (t), vo (t), po (t))Sy (t) dt = t1

t 2     t 2

^J  J SV '(т ) Mvy (т, yO (т ) ,

1 1 L t

vo (т), po (т)) Qi (т, t) dt Sv (t) dt,

t ₂ t ₂

= JJ Sv,(т)

t ₁ t ₁

t ₁

J Sy '( t ) Myy ( t , yO ( t ) , vO ( t ) , pO ( t )) Sy ( t ) dt = t0

t ₂

J   Qi( t,т ) Myy ( t , yo ( t ) , vo ( t ), Po ( t )) Q1 (t , s ) dt тах(т, s)

S v ( s ) dsd т .

Полагая a2^ (y° (t2))

C(т,s) = -Q‘(12,т) Ф2 dy2 k 2Qi (12,s) +

+ ^f    Q‘(t,т)Myy (t,yo (t), vo (t), po (t))Qi (t,s) dt max (т, s)

и учитывая тождества (54)-(56) в неравенстве (53), получаем t 2 t 2

j j Sv '(т) C (т, s) Sv (s) dsdт + t1 t1

t 2

t 2

+ 2 j j S v ' ( т ) M_V y ( т ,y ^o ( т ) , v ^o ( т ) , p ^o ( т ) ) Q i ( т , t ) dt S v ( t ) dt +

t 1

t                                                                                                 _ t 2

+ j S v ‘ ( t ) M_w ( t , y o ( t ) , v ^o ( t ) , p ^o ( t ) ) S v ( t ) dt <  0.

t ₁

Теорема 1. Для оптимальности классической экстремали ( u ^o ( t ), v ^o ( t ) ) в задаче (1)-(4) необходимо, чтобы неравенства (52), (58) выполнялись соответственно для всех S u ( t ) e R , t e T 1 и S v ( t ) e R^q , t e T ₂ .

Непосредственным следствием теоремы 1 является теорема 2.

Теорема 2. Для оптимальности классической экстремали ( u ^o ( t ) , v ^o ( t ) ) необходимо, чтобы выполнялись соотношения:

u‘Huu (0,xo (0), uo (0), И (0))u < 0, для всех 0 e [t0,t1), u e Rr, v ‘ M (£,yo (^), vo (£), po (^)) v < 0, для всех £ e [t1,12), v e Rq.

Утверждение теоремы 2 есть аналог условия Лежандра — Клебша [9; 10].

Изучим случай вырождения аналога условия Лежандра — Клебша.

Определение 1. Классическую экстремаль ( u ^o ( t ) , v ^o ( t ) ) назовем особым в классическом смысле управлением, если для всех 0 e [ t ₀ , t 1 ) , u e R^r и £ e [ t 1 , 1 ₂ ) , v e R q выполняются соответственно соотношения u ‘ H „„ ( 0 , x ^o ( 0 ) , u ^o ( 0 ) , И ( 0 ) ) u = 0, v ‘ Mw ( ^ , y o ( ^ ) , v ^o ( ^ ) , p ^o ( ^ ) ) v = 0.

Предположим, что ( u ^o ( t ) , v ^o ( t ) ) — особое в классическом смысле оптимальное управление, ц — произвольное натуральное число, l j >  0, j = 1, ц — произвольные числа, u j e R^r ( v j e R q ) — произвольный вектор, ⁰ j ^{e [ t} 0 , t i ) ⁽ ^ j ^e [ t i , t 2 ) ) , ^j = 1, Ц ^{( t} 0 <  ⁰ i <  ⁰ 2 < ... < ⁰ ц < t i ) , ( t 1 <  ^ 1 <  ^ ₂ < ... <^ _ц < 1 ₂) — произвольные точки непрерывности управления u ^o ( t ) ( v ^o ( t ) ) .

Положим

г

5uE (t ) = Z^ (t - £; e, -1 j - uj) - j=1

А

г

^{5 и} ц ⁽ t ) = Z ^{5 v ( t - £} ; 6 ^- l j ^- v j ) ^-

V             j = 1                        7

где 5 u ⁽ t - £ ; e j - 1 j - u , ) ⁽ 3 v ⁽ t - £ ; 6 j - 1 j - v , )) — игольчатого типа управляющей функции u ^o ( t ) ( v ^o ( t ) ) - определяемая формулой

вариация

5 u ( t - £ ; e , - l ,. - u , ) =

u , -

V^е , - ⁶ . + , ) ■

0- t g t,\ [ e , - e , + l , £ ) -

5 v ( t - ^£ ; ^ j - l j -у^ = <

v

L , ⁶ ■ , ) ^-

- t G T2\ L,^ + l,£ )J

Суммирование вариаций (61) ((62)) определяется аналогично работам [15-17].

Учитывая (59) ((60))- в неравенстве (52) ((58)) имеем:

£ ²

г                            г

Z l.lju ‘ к (e-j u.+Zlu‘ Hux (e-xo (e) - uo (ej- v° (e))x     <63>

_ .' - j = 1                                              . = 1

i - 1

X l . f u ( e -x ^o ( e . ) - u ^o ( e . ) ) u . + 2 Z l j F ( e - e j ) f u ( e , -x ^o ( e , ) - u ^o ( e j ) ) u

г г

г                              г

Z l . l j V ’ N ( 6 - 6 , ) V j + Z l VM vy ( 6 - y ^o ( 6 ) - v ^o ( 6 ) - P o ( 6 ) )

i - 1

X l.Q1 (6-6.)V.+ 2ZljQ1 (6-6j)

( г ² ) < 0.

Из неравенства (63) ((64)) в силу произвольности £ (г) следует- что г                            г

Z l.lju ‘ к (e-ej.) uj+Zlu‘ Hux (e-xo (e)- uo (ej- v° (e>

X

i - j = 1                                              i = 1

i - 1

l . f u ( e - x ^o ( e . ) - u ^o ( e . ) ) u , + Z l j ^( e - e j ) f u (e_P x ^o ( e j ) - u ^o ( e j ) ) u j < 0-

г

'‘ N ( 6 - j V j + Z l . VM vy ( 6 - y o ( 6 . ) - v ( 6 . ) - p ( 6 . ) )

i - 1

X l.Q1 (6.-6) V.+ 2 Z ljQ1 (6-6j) Vj < 0.

I                L                       j=i                   J

Таким образом- доказана теорема 3.

Теорема 3. Для оптимальности особого в классическом смысле управ

ления (uo (t),vo (t)) необходимо, чтобы для любого натурального числа ц неравенство (65) ((66)) выполнялось для всех lj >0, j = 1,ц, 9j^\t0,tx)

fe^,t2)), j = 1Ц,  (tо < 91 < 9 <... <0Ц< ti)  ((ti < £ < ^2 <... <^ц< t2))  и u,e R j R).

Необходимое условие оптимальности (65) ((66)) относится к классу многоточечных необходимых условий оптимальности особых в классиче ском смысле управлений [12; 15-21].

Непосредственным следствием теоремы является теорема 4.

Теорема 4. Для особого в классическом смысле оптимального управ ления (uo (t), vo (t))

поточечное неравенство

u ‘ \ K ( 9 , 9 ) + H ux ( 9 ,x ( 9 ), u ^o ( 9 ) ) ^ ° ( 9 ) ) f ( 9 ,x ( 9 ) , u ^o ( 9 ) ) ] u <  0, (67)

(v'[N(£,^) + M (^,yo (^), vo (^), po (^))gv (£,yo (^), vo (^))]v < 0) (68) выполняется для всех u e Rr (v e Rq) 9 e \t0,11) (^ e \t1,12)).

Следует отметить, что необходимое условие оптимальности (65) ((66)) остается в силе также при вырождении условий оптимальности (67) и (68).

Заключение

В работе впервые рассматривается задача оптимального управления с переменной структурой, описываемая в различных отрезках времени дифференциальными и интегральными (типа Вольтерра) уравнениями.

При предположении открытости области управления доказаны необходимые условия оптимальности второго порядка, позволяющие при вырождении аналога условия Лежандра — Клебша доказать многоточечные необходимые условия оптимальности особых в классическом смысле управлений. Они позволяют существенно сузить множество классически особых управлений, подозрительных на оптимальность и остаются в силе при вырождении аналога условия Габасова — Кирилловой [10].