Analysis of the Avalos-Triggiani problem for the linear Oskolkov system of the highest order and a system of wave equations

Let Q be a bounded domain in R n ,n = 2, 3, with sufficiently smooth boundary dQ. Let u = col(u 1 , u ₂ , ..., u _n ) be a n — dimensional velocity vector n = 2, 3 , the scalar function p be a pressure, and the vector w = col(w 1 .w ₂ , ...,w _n ) be a vector of displacement of a body, which occupies the domain Q _s , and is immersed in a fluid occupying the domain Q f . Therefore, Q = Q s U Q f , Q s П Q f = dQ s = r s is the common boundary of Q s , and Q f . Let us denote the outer boundary of Q f by r f (see Fig. 1). Our goal is to investigate the Avalos-Triggiani problem [1,2] for the case when the fluid in Q f is an incompressible viscoelastic Kelvin-Voigt fluid of the highest order K ( K = n 1 + ... + n _M ) [3]. The considered mathematical model is determined by the system

M n m - 1

(1 — K V^u t — v V 2 u + (u • V )u — ^ ^ A m,s V ² w _m,_s + V p = 0

m =1 s =0

V (t,x) G (0,T] x Q f = Q Tf ,

∂ w m, 0 ∂t

= u + a m W m, 0 , a m G R - , m = 1, M

^{V ( t} , x) ^{G Q} Tf ,

∂wm,s dt = SWm,s-1 + am Wms, S =1, Пт —

^{V ( t} , x) ^{G Q} Tf ,

V- u = 0,       V (t,x) G Q Tf ,

w _tt — V 2 w + w = 0    V (t, x) G (0, T ] x Q _s = Q _Ts

with the boundary value conditions ulrf = 0,       V(t,x) G (0,T] x rf = rTf,

Wm,slrf = 0,       V(t,x) G rTf, u = wt,       V(t,x) G (0,T] x rs = rTs,

∂u ∂w

-     = pv      V(t,x) G rTs(9)

∂ν ∂ν and the initial value condition

(w(0, • ), w t (0, • ), w i , o (0, • ),..., W M,n m — i (0, • ), u(0, • )) = = (w o , w i , w 0 , o ,..., w M,n m — i ) ^G H ,

wher e H = ( H 1 (Q s )) ⁿ x (L 2 (Q s )) n x H i , o x ... x H m^- i xH f and H m_s = (L 2 (Q s )) ⁿ , m = 1, M,s = 1, n m - 1, H f = { f G ( L 2 (Q f )) n : V • f = 0 in Q f and [ f • v] | _r f = 0 } .

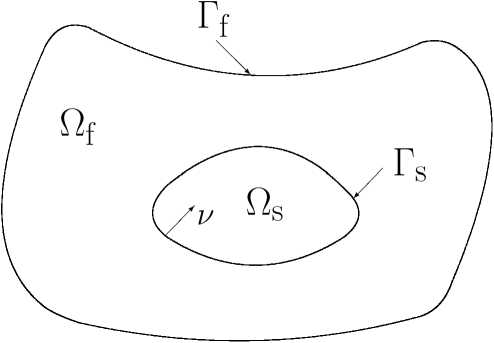
Fig. Physical model

In system (1), the parameters κ and µ characterize the elastic and viscous properties of the fluid, respectively, the parameters A _m,s determine the time of pressure retardation (delay), v is a unit normal vector. In the case of a zero-order Oskolkov system, i.e. K = 0, and к = 0 , problem (1) - (9) was investigated in [1,2], and for K = 0 and к = 0 - in [4,5]. The results of this work generalize the results of [6, 7] to the case of the Kelvin–Voigt model of the highest order.

• 1.    Reduction to the Cauchy problem

Following [1,2], we assume that p ( t ) satisfies the following elliptic problem:

Ap = 0 in QTf, ∂u ∂w p = dV •v - aV •v on rTs’                      (ii)

dP = Au • v on r Tf .

∂ν

Then the pressure p can be represented as follows:

p(t) = D s { ( , t

• ^v-- dV~ • ^V ) r } ⁺ N f ^{((A u (t)} • ^v ) r _Tf )

in    Q Tf ;

where the Dirichlet map D s is defined by the relations

{ A h = 0 in Q f , dh= g on  ^Г ’

— = 0 on rf ’ ∂ν and the Neumann map Nf is defined by the relations

{Ah = 0 in Qf, h = 0 on rs, ∂h dv =g on rf •

Then original system (1) – (5), which describes the interaction of the fluid and the body immersed in the fluid, takes the form

M n m - 1

(1 - kV ² ) u t - v V ² u + ( u • V )u - EE A m,s ^V 2 w m,s + G 1 w + G 2 u = ^{0     (12)}

m =1 s =0

V (t’X) G (0’T] x Q f = Q Tf ’

∂ w m, 0 = u + a ∂t	m W m, 0 ’ a m G R - ’ A m,s G R + ’ m = 1 ’ M      V ( t’X ) G Q Tf ’     (13)
∂ w m,s ∂t	= S W m,s - 1 + a m W m,s ’ S =1’ П т - 1       V (t’ x) G Q Tf ’         (14) V- u = 0’                                    (15)

w tt - V 2 w + w = 0 with the boundary value conditions	V (t’X) G Qts	(16)
u| r f = 0 ’	V ( t’X ) G V Tf ’	(17)
w m,s | r f = 0 ’	V (t’X) G ? Tf ’	(18)
u ≡ w t ,	V (t’X) G Г т5 ’	(19)
where G i w = V{ D s { ( tWt l	• V ) r }} in Q Tf ’
G 2 u = -V{ d , { ( ^V) F Ts } +	N f ((A u ( t) ■ v) r Tf ) }    in Q Tf •

Based on the corresponding results for the operators L and M [8] , problem (12) – (19), in which pressure is excluded, will be written as an abstract Cauchy problem

Lv = Mv,  v(0) = v ₀ ,                            (20)

Here v = col(w,w t , W i , o ,... W m, o , W i , i , ..., W i ,i i ..., W m, i , ..., W m,1 m ,u ) , where l m = П т - 1,m = 1,M .

We study the problem (20) using the results obtained in [9–12].

Lemma 1. Let к E R , ^ E R + , the operators L and M be linear continuous operators from G to H (L,M E L ( G , H ) ), then there exists L - E L H Here is the space G = ( ҢШ П x ( H ² (Q _s )) n x £, 0 x ... x Ө м,_П т — 1 x G f , where G m,_s = ( H ² (Q _S )) n , m = GM s = 1, n m - 1, G f is closure according to the norm of the space ( H ² (Q _s )) of the space of infinitely differentiable solenoid functions such that (17) – (19) are fulfilled.

Theorem 1. For any к E R , ^ E R + and v ₀ E G , there is the unique solution to the problem (20) v E C “ ((0 ,T ], G)

In conclusion, we note that the corresponding stochastic models can also be considered using the approach outlined in [13–15].

Acknowledgments. The work was carried out within the framework of solving problems for the development of the laboratory of Differential Equations and Mathematical Physics of Yaroslav-the-Wise Novgorod State University. The authors express their gratitude to Professor G.A. Sviridyuk for his attention to the work and discussion of the results.