Analysis of the Existence of Periodic Solutions of the Systems of Nonlinear Differential Equations with a Small Parameter

1.    Introduction and Assistive Information

Many natural processes are oscillatory. In the mathematical formulation, such processes correspond to problems that have periodic solutions. Oscillatory processes are usually described by differential equations. A typical example is an equation of the form:

x + x = ^ • f ( x, x ) ,

where ^ is a small parameter. It is known that for ^ = 0 equation (1) has periodic solutions. If ^ = 0, then some perturbations arise in the right-hand side of this equation and, possibly, periodic solutions do not exist. Therefore, the problem is to find conditions under which the equation (1) has periodic solutions.

The study of the system of the form (1) originates from the work A. Poincare [1] and A. M. Lyapunova [2]. Among the many works devoted to the further development of the theory of a small parameter, it is sufficient to mention the works of B. I. Bogolyubov [3], I. G. Malkin [4], J. Guckenheimer [5], A. N. Tikhonov [6], A. D. Morozov [7] and others.

The determining role in the study of equations with a small parameter is played by the linear parts of the equations, the properties of which allow us to study the issues of the existence of periodic solutions of nonlinear equations.

The transition to equations with “essential” nonlinearities, as a rule, requires the development of fundamentally new approaches and methods. A significant contribution to the theory of such equations was made by the works of M. A. Krasnoselsky and his students, Yu. I. Neimark, V. A. Pliss, F. Hartman and others. In these works, topological, qualitative and approximate methods for studying various classes of nonlinear equations were developed.

According to the Poincare method, the solution to the equation (1) is sought in the form [1] x(t) = x o ( t ) + ^x i (t) + ^ 2 X 2 ( t ) + ... + ^ n X n (t) + ...

By equating the coefficients of the same powers of µ , we obtain a system of recurrence relations, for each of which it is necessary to use methods of variation of arbitrary constants to find a solution. However, there are systems in which the use of this method is not effective. An example of such a system could be a nonlinear system of the form

( x = У,

1 y = ^ • x • cos x — x, where µ is a small parameter.

For such systems, other alternative methods are used [8].

Nonlinear systems depending on a small parameter were also the subject of research by L. S. Pontryagin [9] and others (see, for example, [10, 11]). Let us briefly present some auxiliary information from the theory of dynamic systems on the plane and from the general theory of nonlinear analysis (see, for example, [12–16]). Let us consider a system of the form

^X = - TH + VP ^{( x,}y,V), y = dH ⁺ vq ^{( x,}y,v).

For ^ = 0 we get a Hamiltonian system ∂H ∂H x = - ay, y = ax, the integral of which is H(x,y) = C. It is assumed that for the considered values of C (C1 < C < C2) the curves H(x,y) = C are closed curves. Let x = ^(t,C), y = ^(t,C) be a solution of the system (3) corresponding to some curve H(x,y) = C.

Consider the integral

τ

I(C Ч

[р^-Ж ⁰⁾/ - q^,^, ⁰V]

dt,

where т = т(C ) — period of functions ^ and ^ . This function is called the Pontryagin function. Along with this function, the function is considered

τ

I'(C ) = I \p'_x W, 0)

+ q y (^Ж ⁰⁾] dt.

Theorem L. S. Pontryagin’s [12, p. 203]. If for some value C = C o the conditions are satisfied

I (Co) = O, I ‘(Co)=0, then there are numbers e > 0 and 6 > 0 such that:

• a)    for anyone ц, | ц | <  6, system (2) has in e — neighborhood of the curve H(x,y) = C o one and only one limit cycle, and at ц ^ 0 it contracts to this curve;

• b)    this limit cycle is a rough limit cycle, stable, when ц • I ‘ ( C o ) <  0 , and unstable, when Ц • I ‘ (C o ) >  0 .

The conditions of Pontryagin’s theorem assume that the functions p and q are differentiable. We study the conditions for the existence of a cycle for the more general case, when the functions p and q are only continuous.

For proof of the main statements obtained in the work, topological methods are used, in particular, the apparatus of rotation of vector fields. These methods originate from the works of J. Leray and Y. Schauder [17]. Below we will provide the necessary information from this theory.

First of all, let us recall some definitions and concepts (see, for example, [13]).

Let E be a real Banach space and Q C E be a bounded domain. Let a completely continuous operator A acting in E be defined on the closure Q of the domain Q, and let Ax = x for any x G Q; where Q is the boundary of the domain Q. Then an integer characteristic Y (I — A, Q) is defined, which is called the rotation of the completely continuous vector field Ф х = x — Ax on the boundary Q of the domain Q.

Two non-degenerate on Q (i. e. not taking zero values on Q) completely continuous vector fields

Ф o x = x — A o x,  x G Q ,

Ф1x = x — A1x,  x G Q, are called homotopic on Q if there exists a family of non-degenerate on Q vector fields

Ф(Х, x) = x — A(X, x), x G Q, X G [0,1], such that the operator A(X, x) is completely continuous with respect to the set of variables X and x, and

Ф(0,x) = Ф o x, Ф(1 ,x ) = Ф ₁ x.

The homotopy relation of vector fields has the following properties:

Property 1.1. If Ф о and Ф 1 homotopic on Q, that

Y (Ф o , Q) = Y (Ф 1 , Q) .

This property allows us to reduce the calculation of the rotation of complex vector fields to the calculation of the rotation of simpler fields.

Property 1.2. If the likenes A Q of the domain Q lies in the subspace E o C E and Q П E o = 0 , then the field Ф x = x — Ax is defined on the boundary Q o of the domain Q o = Q П E o with a value on E o . Let Q o = 0 . Then the equality y (Ф , Q) = Y (^ ; Q o ) is true.

Property 1.3. Let a completely stable vector field Ф x = x — Ax be non-degenerate on the boundary of Q bounded domain Q and continuity of its closure Q and Y (Ф , Q) = 0. Then the field Ф has at least one singular point in the domain Q.

It follows from property 1.3 that each sign of non-zero rotation of the field Ф on the boundary Q of the domain Q is a sign of the existence of at least one solution of the equation Ф x = 0 in the domain Q.

2.    Statement of the Problem and Main Results

Let us consider a system of differential equations, the vector notation of which has the form x = Ax + ef (x,e),                                  (4)

where x = ( x i , X 2 , X 3 ) € R ³ , A is a square real matrix, f ( x, e ) — a continuous vector function over a set of variables ( x,e ) € R ³ x [ — e o , e o ], e o >  0, e — parameter. In what follows, it is assumed that the spectrum a ( A ) of the matrix A has the representation: a ( A ) = {± ie,Y } , ^e >  ⁰ , Y = ⁰

Of interest is finding conditions on the vector function f ( x,e ) under which there exist non-zero periodic solutions of the system (4) for sufficiently small non-zero values of ε .

For the study of the question of the existence of cycles, the starting point was the classical theorem of L.S. Pontryagin [1, p. 214], which was formulated for systems of equations on a plane under the assumption of analyticity of the function f ( x,e ) with respect to the set of variables x, ε . In contrast to Pontryagin’s conditions, below we do not assume differentiability of the function f ( x, e ); the continuity condition of this function with respect to both variables is sufficient. We also note that the system we are considering is not Hamiltonian. It should be noted that in the case of x € R ² the system (4) was considered in the work [8].

Under the assumptions made regarding the spectrum of the matrix A, there exists a nonsingular matrix U, such that replacing x = Uy the system (4) leads to the system yi = вУ2 + egi(yi,y2,y3,e)

< ^y2 = - ^вУ 1 + ^eg 2 ⁽ У 1 ,У 2 ,У 3 ,£)                              ⁽⁵⁾

,У’ з = Yy 3 + ^eg 3 ⁽ y i ^,y 2 ^,y 3 ^{,e )} .

Note that systems (5) and (4) are equivalent.

On the right side of the system (5) we define an analogue of the Pontryagin function [1]

2 π

F M

[ g ₁ (p cos p,p sin p, 0 , 0) cos p + g ₂ (p cos p,p sin p, 0 , 0) sin ^ ] dp.

Let us recall that the norm in the space of continuous functions is defined by the following equality: ||x( t ) || = max t | x ( t ) | , where | • | is the euclidian norm in space R ³ .

Let us formulate a necessary condition for the existence of periodic solutions of the system (4) at e ^ 0, e >  0.

Theorem 1. Suppose that for some sequence of values e = e k = 0 , e k ^ 0 , for к ^ от the system (4) has a periodic solution x(t + W k ,e k ) = x(t,e k ) , with the smallest period & k = w(e k ) >  0 , satisfying the condition C i ^ ||x ( t,e k ) | <  C 2 , where 0 < C i < C2 — are given numbers. Then there exists p o € [ C i ,C 2 ] , such that F ( p o ) = 0 .

The formulated necessary condition, under some additional restrictions on the behavior of the function F(p) in the neighborhood of the solution of the equation F(p) = 0, is also a sufficient condition for the existence of a periodic solution of the system (4) for small | e | >  0, namely, the following theorem is valid.

Theorem 2. Let p o >  0 be a solution to the equation F(p) = 0 , and in the neighborhood [p o - S o , P o + S o ] points p o , where p o — S o >  0 , function F(p) = 0 for p = p o , and F(p o — S o ) • F(P o + S o ) <  0 . Then the system (4) for sufficiently small values of | e | >  0 has a non-stationary w(e)-periodic solution x(t,e).

The proofs of the theorems are given below.

3.    Transition to Polar Coordinates

For e = 0, system (5) is a linear system, and its general solution has an explicit representation, from which it follows that any solution (y i (t),y 2 (t),y 3 (t)) with initial condition ( y i (0) ,y 2 (0) , 0), | y i (0) | + | y 2 (0) | >  0 is a cycle with period в in the plane ( y i ,y 2 , 0). Therefore, for T >  0 the solution is ( y _i ( t, е),у ₂ (t,E),y 3 (t,E)), | y 1 (0 , e) | + | y ₂ (0 , e) | >  a >  0 satisfies the condition r ² (t,E) = y 2 (t,E) + y 2 (t,E) >  0 for anyone | t | C T for sufficiently small absolute values e and у з (0 , e) .

Let (y1(t), y2(t), y3(t)) be the solution of the system (5), satisfying the condition r(t) = Vy2^) + y2(t) > 0. Believing yi = r cos v,  У2 = r sin V,  Уз = Уз,                         (6)

we get r = E[g1(r cos v, r sin v, Уз,е) cos v + g2(r cos v,r sin v, Уз, e) sin v],

• < v = - в - r [ g i ( r cos v,r sin v,y 3 ,E )sin v — g 2 ( r cos v,r sin v,y 3 ,E )cos v ] ,        ⁽⁷⁾

.Уз = Yy 3 + Eg 3 (r cos v, r sin v,y 3 , e) .

Let us assume that for the solution y ( t ) of the system (5) for a given value of e the righthand side of the second equation of the system (7) is not equal to zero for all t . Then time t can be expressed through the polar angle v ^: t = T ( v ), T ( v ( t )) = t - Let’s define complex functions p ( v ) = r(T ( v )), Y ( v ) = y 3 ( T ( v ))- It is easy to show that these functions satisfy the system of equations

^ρ dϕ dY dϕ

= ^ER i ⁽ p^,Y,v^{,E )} , = ^R 2 ⁽ P^,Y,v^{,E )} ,

where

R i ⁽ P^,Y,v^{,E )} =

p ( g i cos v + g 2 sin v )

R 2 ⁽ P^,Y,v^{,E )} =

- вр - E [ g i sin v - g 2 cos v ] ’ P ⁽ YY + ^Eg 3 )

- вр - E [ g i sin v - g 2 cos v ] ’

g i = g i (p cos v,P sin v,Y,e ) i = 1 , 2 , 3.

Conversely, if p ( v ), Y ( v ) is the solution of the system (8) for a given e and satisfies the condition - вр + E ( g 2 cos v — g i sin v ) <  0, then a monotonically decreasing function is defined

ϕ

^{T (} v ⁾ = ./

pW d^

-вр^) + E(g2 cos ^ - gi sin ^) ’ and vector function (r(t), v(t), Уз(t)) = (p(T-i(t)),T-i(t),Y(T-i(t))) is a solution to the system (7).

Under these conditions, in particular, to each ω -periodic solution of the system (7) (and, consequently, of the system (4)) there corresponds a 2 n -periodic solution of the system (8).

Thus, we have established the validity of the following lemma.

Lemma 1. If x ( t ) = Uy(t) is a solution (4) , the function (r(t), v(t),y 3 (t)), defined by the equalities (6) , satisfies the condition E(g 2 cos v - g i sin v ) <  в^г, then vector function ( p ( v ) , Y ( v )) = (r(T(v)),y 3 (T ( v ))) is a solution to the system (8) .

Conversely, if (p(p),Y(p)) is a solution of the system (8) , and the function p(t) is determined from the equation T(p) = t, then the vector function (r(t),p(t),y 3 (t)) = (p(p(t)), p(t),Y(p(t')')') is a solution of the system (7) , where the function T(p) is defined by the equality (10) .

If, in particular, the function x(t) = Uy(t) is ш-periodic, then the corresponding function (p(p),Y(p)) is 2n-periodic, and ш = T( — 2n).

4.    Proof of Theorem 1

<1 Let for some sequence of values e = Ek = 0, Ek ^ 0, for k ^ от the system (4) has a periodic solution x(t + Шк,Ек) = x(t,Ek) with the smallest period Шк = ш(Ек) > 0, satisfying the condition 0 < Ci C ||x(t,Ek)\ < C2. Then y(t,Ek) = U-1y(t,Ek) is a solution of the system (5) for e = Ek. Without loss of generality, we can assume that the sequence y(t,Ek) uniformly converges to some function yo(t). The function yo(t) is a bounded solution of the system (5) for E = 0. It follows that the third coordinate of the sequence y(t, Ek) uniformly tends to zero. Therefore, after the transition to polar coordinates (6) for the obtained sequence (r(t,Ek),p(t,Ek),y3(t,Ek)) the first coordinate r(t,Ek) > 0. According to Lemma 1, this sequence corresponds to a sequence of 2n-periodic solutions p(p,Ek), Yfa,Ek) of the system (8):

I

d^d^ k ) = ^E k R 1 ⁽ p ⁽ p^,E k ^{) ,Y (} p^,E k ),^^,E k ) , dY^T ) = R 2 ⁽ P ⁽ ^^,E k ^{) ,Y (} ^^,E k ),p^,E k )■

Let us integrate the first equality of this system from 0 to 2 n over the variable ^ , taking into account the 2 n -periodicity of the function p(p, E k ). Reducing the resulting equality by E k , we have

2 π

У R i (p(p,E k ),Y(p,E k ),p,E k ) dip = 0.

By definition of the sequence (p(p,E k ),Y(p,E k )), the first coordinate uniformly converges to some number p o ^ C i , the second coordinate to zero. Therefore the sequence R i (p(p,E k ),Y(p,E k ),p,E k ) converges uniformly to - 1 ( g i ( p o cos p, p o sin p, 0, 0) cos p + g 2 (p o cos p, p o sin p, 0, 0) sin p ). Therefore, after passing to the limit under the integral sign at k ^ от , we obtain that p o is a solution to the equation F(p) =0. >

5.    Proof of Theorem 2

• < Let us consider a system of integral equations

p ⁽ p) ^- p ^{(2 n )} = ^Ef ^R i ⁽ p ^{( s )} , ^{Y ( s )} ,s, ^{e ) ds}, ⁰ ϕ                                                (11)

Y(p) - Y(2n) = f R2(p(s),Y(s),s,E) ds, where are the functions Ri(p(s), Y(s), s, e), R2(p(s~), Y(s), s, e) are defined by equalities (9) in the domain e(g2 cos p — gi sin p) < вг. Every solution of the system (11) defines a 2n-periodic solution of the system (8), and conversely, to each 2n-periodic solution of the system (8) there corresponds a solution of the system of integral equations (11). If we show that the system (11)

has a solution for small values of £ >  0, then, according to lemma 1, the system (4) also has a periodic solution. Thus, theorem 2 will be proved. At the boundary of Q(5 o ,oq) region

^Й,М = {(p(p),yЫ): llp(p) -poll < ^o, IIYЫН  0 is a fixed number, in the space of continuous vector functions C[0, 2n] we consider families of completely continuous vector fields

^ ⁽ P>^{Y,e )(} V ⁾

ϕ рЫ -р(2п) -£JRi(p, Y, s,e) ds,

ϕ

Y ( p ) - Y (2 п ) - У R 2 (p, Y, s, £ ) ds

^ ⁽ P^{,Y,e )(} P) =

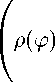
ϕϕ

— p ^{(2 n )} + £ yF⁽ p ^{( s ))} ds, Y ⁽ p ) ^- Y ^{(2 п )} + в YY ^{( s )} ds

We will show that for sufficiently small £ >  0 on the boundary Q( J o ,^ o ) of the domain ^( ^ 0 , ^ o ) these vector fields are linearly homotopic: there exists £ o >  0, such that

A$⁽P^,y,£⁾⁽^ + ⁽ 1 ^- А)Ф(р,У,£)(^) = ⁰

⁽V A ^{g [0 ,} 1 ^{]) (}V £ ^{G (0 , £} o ^{]) ( p}, Y ) G ^( J o , ^ o ) .

Indeed, if we assume the opposite, then there are sequences £ k ^ 0, £ k >  0, A k G [0 , 1], ( P k ,Y k ) G Q( £ o ,M, such that

'                              p

P k ( p ) - P k (2п) = £ k / [A k R i (p k (s), Y k ( s ) ,s,£ k ) - (1 - A k ) F ( p k (s))] ds, ϕ ⁰                                                               (14)

^Y k ⁽ p ) ^{- Y} k ^(2п) = } ^^A k R 2 ⁽ P k ^{( s )} , ^Y k ^{( s )} , ^s, ^£ k ) ^{- (1 - A} k ) в ^Y k ^{( s)}J ds.

From the limited sequence (pk,Yk) and equality (14) its equicontinuity follows. Therefore, without loss of generality, we can assume that it converges to some vector function (p*(p),Y (p)) and Ak ^ A*. Note that from the equalities (14) it follows that p*(p) = p*(0), а Y*(p) is a solution to the equation dY = - Yy dϕ β and satisfies the condition y(0) = Y(2n). Therefore, (p*(p),Y(p)) = (p*(0),0). Further, from the condition that (p*(p), Y*(p)) G Q(5o,oq) it follows that p*(p) = po + J or p*(p) = Po - J.

On the other hand, assuming equality (14) p = 2 n and reducing the resulting equality by ε k , we have

2 π

[ ^A k R 1 ^{( p} k ^(s), ^Y k ^(s), ^s, ^£ k )     ^{(1 A} k ^{) F ( p} k ^(s)) ] ^{ds 0 .}

Let’s move to the limit at k ^ w in this equality. We get

/[ - p ( g i < p - < s ) 0

cos s, p * ( s ) sin s, Y * (s), 0) cos s

+ g 2 ( p * ( s ) cos s,p * ( s )sin s,Y *

(s), 0) sin s) - (1

- A * ) F ( p * (s))

ds = 0 .

Given that Y =0, p * ( s ) = const G [ p o — e,p o + e ], it follows from the last equality that p * ( s ) = p o . This contradicts the condition that p * ( ^ ) = p o + 6 or p * (A = p o — 5 . The obtained contradiction proves that for sufficiently small e >  0 on the boundary Q( 5 o , a o ) of the domain Q( ^ o ,a o ) the vector fields (12) and (13) are linearly homotopic.

Now let us consider the family of vector fields

ϕ

2 π

^ A ⁽ p^{,Y,e )(} ^ = p^

— p (2 n ) + e у F(p(s)) ds + eA J F ( p ( s )) ds,

ϕ

^{Y (} ^ )

—

ϕ                 2 π

Y (2 n ) + Y IY ( s ) ds + YA [ Y ( s ) ββ

0 ϕ

ds

at 0 C A C 1. It is easy to show that there exists e o >  0, such that for all 0 < e C e o and any 0 C A C 1 on the boundary of Q( 6 o ,a o ) the domain Q( 6 o ,a o ) Фд^ , Y, e )( ^ ) = 0. In particular, for A = 0 we obtain the original vector field (13), and for A = 1 we obtain

2 π                                      2 π

^ i ⁽ p^{,Y,e )(} ^ =

p ⁽^) - p ^{(2 n )} + ^e У F ⁽ p ^{( s ))} ds, ^{Y (} ^ ) - ^{Y (2 п )} + в У ^{Y ( s ) ds}

Operator

2π                 2π e у F (p(s)) ds, y/y(s) ds],

defining the vector field Ф 1 , acts from the closure of the domain Q( 5 o ,a o ) of the space of vector functions C [0 , 2 n ] into the subspace of constant functions. Therefore, according to the Leray-Schauder lemma [17], the rotation of the completely continuous vector field Ф 1 on the boundary Q( 6 o ,a o ) of the domain Q( 6 o ,a o ) coincides with the rotation of its restriction

_

Ф 1

(p,Y )= ^2neF ( p ) , 2 nYY^

on the boundary of the intersection of the region ^( ^ o , a o ) with the space of constant vector functions, that is, a rectangular region { ( p, Y ) : | p — p o | < 5 o } , | Y | < a o .

Thus, the equalities are valid

7 ^(ф 1 , ^Q) = Y ^(ф 1 , ^Q) =

sign F (p o + g o ) — sign F (p o — g o ) 2

Therefore, rotation 7 (Ф , Q) fields (14) on the boundary Q of the domain Q are non-zero. This implies the existence of a 2 n -periodic solution of the system of equations (8) in the domain Q, and by lemma 1 the system (4) has an w -periodic solution for sufficiently small e >  0. >

Remark. The results above can be extended to the case where the dimension of the solution space is greater than three.

6. Example

Consider a system of the form

X 1 = - X 1 - X 2 + Х з + Ef 1 ( x i ,X 2 ,X 3 ,e ) ,

< X2 = - X 2 + Ef 2 ( x i ,X 2 ,X 3 ,e ) ,                                     ⁽¹⁵⁾

Х^з = -2xi + X3 + ef3(xi,X2,X3,e), where f1 =

( X 2 - X 1 ) ² + ( Х з - X 1 ) ² - 2

• sign

(( Х 2 - Х 1 ) ² + ( Х з - Х 1 ) ² - 2) • ( х з - x ₂ ) + ЕХ 2 ,

f 2 = 2 •

( Х 2 - Х 1 ) ² + ( Х з - Х 1 ) ² - 2

• sign ^( Х 2 - Х 1 ) 2 + ( х з - Х 1 ) ² - 2^ • ( х з - Х 2 ) + ЕХ 2 ,

f 3 = ( Х 2 - Х 1 ) ² + ЕХ з -

The linear part of the system (15) is determined by the matrix A :

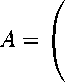
- 1 0

-

- 1

1 0

- 1 0

The spectrum a(A) of the matrix A has the present: a(A) = {±i, -1}. Accordingly, we can assume that in the system (15) the matrix A has a Jordan presentation. Then the system corresponding to the system (5) has the following form yi = У2 + ед1(У1,У2,Уз,е),

^{< y} 2 = - У 1 + ед 2 ⁽ У 1 ,У 2 ,У з ,£),

УУз = -Уз + ?дз(У1,У2,уз,£), where д1(У1,У2,Уз,е) = -2у

2 ^У 2 ⁺ 2 ^У 2

-

i   А

9 sign 77

2       \ 2

о У ^{2 +} 2 У 2

^- 2) ^{У 1 +}(4 ^{у 2}

-

2 У 1 У 2 +4 У 2 ]~^ууз,

д2(У1,У2,Уз,£) = 4У2 - 2У1У2 + 4У2, дз(У1,У2,Уз,у) = 2 •

2 ^У 2 + 2 ^У 2

-

1 -„<12,12

2 ^sign <2^{У1 +} 2 ^У 2

-

2) У 1 + ЕУ з -

After the transition to the polar coordinate system using formulas (6), the system (16) will take the form р = Ф1(рcosр,рsinр,Уз,е) • cosр + д2(рcosр,рsinр,Уз,е) • sinр],

⁽ р = - 1 + Р [ д 2 ( р cos р,р sin р,У з ,е) • cos р - д 1 ( р cos р,р sin р,У з ,е) • sin р ] , .Уз = - Уз + ^уд з (р cos р,р sin р,У з ,е)

where

g i ( p cos p,p sin p,y 3 ,e

) = ^{- 2}p ^    2 ⁽ P 2 - ^l) sign ( 2(P 2 - i) )

cos p +4 p ² - 2 p ² cos p sin p - еу з ,

g 2 (p cos p,p sin р,у з ,е) = 4 p ² - 2 p ² cos p sin p,

g 3 ( p cos p,p sin р,У з ,е) = 2 p •

Let’s introduce the functions

2( p 2 -ⁱ⁾

sign Q( p ² - 1)^ cos p + ЕУ 3 -

g ii ⁽ p) = ^- 2 p •

sign 2pp — ч) .

g i2 ⁽ p ) = g 2i ⁽ p ) = p ² ,    g 22 ⁽ p ) = 0

P i^ ) = cos p,  P 2 ⁽ p ) = ^Q i ⁽ ^ ) = 4

and we rewrite the last equalities in the form

-

2 cos p sin p,   Q 2 ( y ) = 0 ,

g i = g ii (p)P i (p) + g i2 P 2 ( p ) - еу з ,    g 2 = g 2i Q i ( p ) .

The function F(p') corresponding to the system (16) will take the following form

^{F (} p ) = ^{- 2 n}p

sign

(2

2 - 4

The function F(p) at the point po = I is equal to zero. If we take the neighborhood [po + ^o, po - ^o] point po, then at 5o G (0, I) function F(po + ^) < 0, and F(po — ^o) > 0. It follows that the conditions of theorem (2) are satisfied, therefore, the system has a periodic solution for small е > 0. Note that here the function F(p) is continuous, but not smooth, since at the point po = i it has no derivative.