Ant colony system algorithm with dynamic pheromone updating for 0/1 knapsack problem
Автор: Abdullah Alzaqebah, Ahmad Adel Abu-Shareha
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 2 vol.11, 2019 года.
Бесплатный доступ
The 0/1 Knapsack (KP) is a combinatorial optimization problem that can be solved using various optimization algorithms. Ant Colony System (ACS) is one of these algorithms that is operated iteratively and converged emphatically to a matured solution. The convergence of the ACS depends mainly on the heuristic patterns that are used to update the pheromone trails throughout the optimization cycles. Although, ACS has significant advantages, it suffers from a slow convergence, as the pheromones, which are used to initiate the searching process are initialized randomly at the beginning. In this paper, a new heuristic pattern is proposed to speed up the convergence of ACS with 0/1 KP. The proposed heuristic enforces an order-critical item selection. As such, the proposed heuristic depends on considering the profit added by each item, as similar to the existing heuristics, besides the order of item selection. Accordingly, the proposed heuristic allows the items that are added at the end to get more value in order to be considered in the beginning of the next round. As such, with each cycle, the selected items are varied substantially and the pheromones are vastly updated in order to avoid long trapping with the initial values that are initialized randomly. The experiments showed that the proposed heuristic is converged more rapidly compared to the existing heuristics by reducing up to 30% of the cycles required to reach the optimal solution using difficult 0/1 KP datasets. Accordingly, the times required for convergence have been reduced significantly in the proposed work compared to the time required by the existing algorithms.
Ant Colony System, Heuristic Optimization, Combinatorial Optimization, Knapsack Problem, 0/1 Knapsack Problem
Короткий адрес: https://sciup.org/15016568
IDR: 15016568 | DOI: 10.5815/ijisa.2019.02.02
Текст научной статьи Ant colony system algorithm with dynamic pheromone updating for 0/1 knapsack problem
The optimization problems are those require searching for the best solution among the set of all feasible solutions[1]. Generally, the optimization problems are enormous, accordingly, in order to promote the advances in solving these problems, the research community has come up with common, generalized and simple forms of these problems. Examples of these common forms are the traveling salesman problem (TSP), the knapsack problem (KP) and the graph coloring problem [2]. The 0/1 knapsack problem is a combinatorial (i.e.: discrete variables) problem that is categorized as an NP-complete problem with an exact algorithm that runs in exponential time.
The 0/1 knapsack problem is formed by the following inputs: A fixed-size knapsack and a set of items and the following output: A selected subset of items, such as, the obtained benefits/values from this subset is maximized while the weights/sizes of the subset is less than or equal to the weight/size of the knapsack. Accordingly, each of the items in the input set can be either be selected or unselected. The selected items are represented by the value 1, while the unselected items are represented by the value 0. Thus, the name 0/1 knapsack problem was given. Besides the 0/1 knapsack problem, there are other forms of the knapsack problems, such as: 0/1 multi-objective knapsack problem [3], multi-dimensional knapsack problem [4], multiple knapsack problem [5] and subset problem [6]. The differences between these problems are either due to the constraints on the input or the output form.
The optimization algorithms were proposed either to solve the optimization problems that do not have known exact algorithms that find the best solution or to solve problems, such as the 0/1 knapsack problem, that have exact algorithms but they consume unaffordable time [7]. The optimization algorithms search the solution space and find a nearly optimal solution in a finite time. Compared to the exact, the optimization algorithms find a nearly optimal solution more rapidly, preserve the computational resources while scarifying limited accuracy.
The presence of the optimization algorithms is related to the significant of the underlying problems. The significant of the 0/1 knapsack problem has gained from its enormous application, such as the resource allocation problems which occur in the financial field, the industrial field, the architecture and other fields. To solve these critical problems, various optimization algorithms were proposed to solve the 0/1 knapsack problem, such as the simulate annealing [8, 9], the genetic algorithms [10, 11], the swarm optimization [12, 13] and the ant system (AS) optimization [14]. The differences between these optimization algorithms with respect to the 0/1 knapsack problem in specific and optimization problems in general, are: the ability to find the optimal solution, the quality of the generated solution, the non-trapping in local optima and the speed of convergence.
Ant System (AS) optimization algorithm was proposed by Marco Dorigo in 1996 [15] and inspired by the foraging behavior of ants in the colony. The ants are communicating with each other during foraging using chemical pheromones that is dropped on the trails. Accordingly, ants are guiding each other by the pheromones that are concentrated on the trails. Overall, the shortest path between the food and the nest is marked with high concentrated pheromones, as illustrated in Fig. 1. The ants start exploring the surrounding for food by following random paths. As the ants find the food, these ants tend to leave pheromones on the way back to the nest that depends on the quality or the amount of the gathered food.
Nest Food
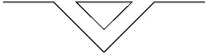
1. All Ants are in the nest. There is no pheromones in the trails
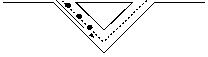
2. The foraging of the ants start. There is a 50% probability that the ants take the shortest path, and 50% of the ants take the other path.
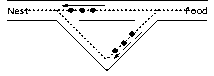
3. The ants that took the shortest path reached the destination earlier and return to the nest faster. Making more journeys and add more pheromones.
Fig.1. Ant Colony Foraging Behavior [17]
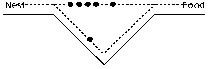
4. The pheromone on the shortest path increase as more ants use it for nest-food travelling journey
AS optimization algorithm simulates the foraging behavior of the ants using artificial ants, each of which construct a solution that follows the representation of the underlying problem. Then, an amount of artificial pheromones that are simulated the actual phenomes, are associated with the constructed solution based on its quality. Running this process for a finite number of cycles lead eventually to find the optimal solution for the underlying problem. AS was empirically proved to find solutions for many problems, including KP, with guaranteed matured solution [16].
A better version of AS is the Ant Colony System (ACS), which uses heuristic patterns besides the associated pheromones to guide the searching process. Although, ACS has many advantages, it has limitation embodied in its slow convergence, as the pheromones, which are used to guide the searching process are initialized randomly at the beginning. In this paper, a new heuristic pattern is proposed to overcome the slow convergence of ACS with 0/1 knapsack problems. The proposed heuristic combines the gathered profit before adding an item with the pheromone updating rules. As such, the proposed heuristic depends on considering the profit added by the item, as similar to the existing heuristics, besides the value gathered so far, which allows items that are added at the end to get more value in order to be considered in the beginning of the next round. Accordingly, with each cycle, the selected items are varied substantially and the pheromones updating is rapidly implemented to avoid long trapping in the initial values. The rest of this paper is organized as follows: Section 2 gives a brief review of the related work. Section 3 discusses the proposed approach with the proposed heuristic mechanism. Section 4 is devoted to discuss the experiments and the results. Finally, the conclusion is given in Section 5.
-
II. Related Work
Several extensions to the popular AS optimization were developed in the last decades. Elitist Ant System (EAS) [18] improved the pheromone updating rules by incorporating all the solutions in the previous cycle with the best solution so far. Only the best solution so far, can contribute to pheromone increment with value equal to one (e.g.: maximum value), while the component of the other solutions contributes with less value and based on their added values. Accordingly, strong increment is added to the components of the best solution to increase the exploitation of the solution space.
Rank-based Ant System (RAS) [19] also modifies the pheromone updating by incorporating the m -best ranked solutions in the previous cycle with the best solution so far.
Min-Max Ant System [20] uses two updating rules, these rules are: Iteration-Based (IB-update), which gives strong bias towards to the best solution in the iteration, however suffers from trapping in local optima and BestSolution (BS-update), which gives even more bias towards the best solution in the iteration so fat.
Ant Colony System (ACS) [21] implements various improvements to AS. First: ACS uses the pseudo-random proportional, by selecting the components of the solution depends on both the pheromones and the heuristic value of each component. Second, ACS uses BS-update with evaporation. As such, only a particular portion of pheromone increment is applied after each cycle. ACS is currently the most utilized versions of the AS.
In order to solve the lacks of pheromones in the initial stages and slow exploration, various approaches were developed, which varies with their nature. The first approach is based on using other optimization with AC, in this context, genetic algorithm were used to explore the search space initially followed by AC [22]. Zhang and Wu [22], for example, proposed to combine ACS with genetic algorithms, which is faster in exploring the solution space, and slower compared to ACS in exploiting the solution space. Accordingly, genetic algorithm is used initially to explore the space followed by exploiting the final solution using ACS. Although ACS solves much of the limitations in AS and its variations, it still suffers from slow convergence, as the pheromones, which are used to guide the searching process are initialized randomly at the beginning. The second approach focus on the heuristic pattern, which are used with the pseud-random in selecting objects at each cycle and accordingly influence the exploring process marginally.
There are three patterns that are used with 0/1 knapsack problem, these are: static, dynamic and squared. In the static patterns, the heuristic is calculated as the ratio of the profit coefficient to the weight coefficient multiplied by the total knapsack capacity. For the dynamic approach, the heuristic is calculated as the ratio of the profit coefficient to the weight coefficient multiplied by the current knapsack load capacity [23]. The squared approach, the heuristic is calculated as the ratio of the square profit coefficient to the square weight coefficient [24]. The dynamic heuristic patterns make varied updating of the pheromones after each cycle compared to the static one.
-
III. Proposed Work
In the proposed approach, the heuristic is integrated with the pheromone updating while changing the order by which the items are added to the knapsack. Accordingly, this creates varied constructed solutions. Overall, the proposed approach focuses on the variability of the item selection process.
-
A. Problem Formation
The 0/1 knapsack problem can be represented by a knapsack of fixed-size, W , and a set of n items, S ={o 1 ,o 2 , .., o n }, in which each item or object, o i , has a value vi and a weight wi . The objective function is to maximize the value of the selected items in the output subject to the limitation of knapsack capacity, as given in (1).
max
∑
XtOt ,
subject to
∑
XiWiW t=l
Wℎere xt ∈ {0,1} (1)
Using ACS, KP can be solved by running multiple ants in each cycle, each of which constructs a solution using the objective function that is given in (1). The probability of choosing an object at each step for each ant depends on the pheromone and the heuristics that are calculated at that object. After each cycle, the pheromones at each object is updated based on the quality of the solution(s) in which the object was loaded, as given in Algorithm 1.
As given in Algorithm 1, in line 1 and line 2, the form of the problem, the number of ants, and the pheromones are initialized. Line 3, line 4 and line 5 initiate looping over cycles, ants and object per-solutions. Object
selection is implemented in line 6 and line 7 stochastically based on the calculation at line 7, where, α: pheromone significance, β: heuristic significance, ρ: evaporation rate and τ: the pheromone concentration value.
Algorithm 1. Ant Colony System for Knapsack Problem
Begin
-
1. Parameter Initialization
-
2. Set initial pheromones
-
3. While (Not Stopping Condition)
-
4. For (1to K) // K is the number of ants
-
5. For ( 1 to n) // n is the number of objects
-
6. Select an object o i with probability
-
7. p i =τ i α* μ i β /⅀ i τα* μβ for wi ≤ W
-
8. EndFor
-
9. EndFor
-
10. Update BestSolution
-
11. Update Pheromones with evaporation
-
12. EndWhile
End
-
B. Convergence Speed-Up Approach
To increase the diversity of the solutions, the order by which the elements are selected is altered, which in turn will create diverse solutions. As known in knapsack problem, the order by which the items are inserted into the knapsack affects the content of the final solution. The first item(s) selected for solution influence the selection of the rest of items. Accordingly, changing the first selected item(s), without effecting the fitness/profit, will change the whole solution, without degrading the results.
To implement such rapid order-critical solution construction, a new heuristic pattern is proposed and integrated with the pheromones updating in order to speed up the convergence process. The proposed heuristic depends on considering the profit of the solution, as similar to the existing heuristics besides the profit obtained so far in the same solution. Accordingly, the value added by any object, depends on its association with other objects. Choosing an object, a then an object b does not have the same influence as choosing b then a.
-
C. Overall Processes
In the proposed approach, each object is given a different pheromone increment rate based on the solution profit and the situation of the knapsack before adding the object. The optimization processes are implemented as given in Fig. 2. First, a set of ants is created, each of which assigned an empty solution. Then, as the ants move from a state to another, an object is added to the underlying solution based on the solution construction process. An ant reaches the final state when the knapsack capacity is reached. After all the ants finish the solution construction process, the heuristic calculation is implemented followed by implemented the pheromone updating process and pheromone evaporation.
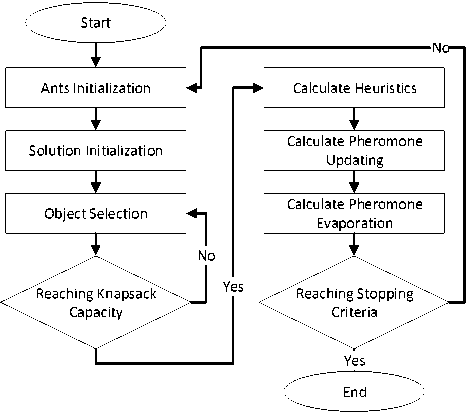
Fig.2. Knapsack Data Categories
-
D. Solution Construction
Each ant constructs a solution by adding an object in each step to the initialized empty solution. An object is selected with a probability value, as given in (2).
рк = [чп^
1 2ЕТ£]“ЕМ£]^
where, τ i is the pheromone concentration on the object i , u i is the heuristic calculated at the object i , α is the pheromone significance and β is the heuristic significance.
-
E. Pheromone Trails Updating
The pheromone associated with each object is updated after each cycle based on the solutions that are formed by that object, as given in (3).
Т (t + 1)=p т(0 + (1-р Ж (3)
where , τ i is the pheromone concentration, ρ is the evaporation rate and Δ τ i is the increase value of the pheromone, as calculated in Equation (4).
Дт = £ 1/(1 + (Vbest - V//Vbes) + vt//vbest solutions where, Vbest is the profit of the best solution so far and V is the profit of the solutions, in which the object i are presented. The variable Vt is the current solution profit and γ is the convergence rate [0-1]. As such, the amount of pheromone at an object increases significantly if the object is added to a loaded knapsack, while the incremental portion is identical to the original ACS, when the object is added to an empty knapsack.
-
F. Heuristic Calculation for Solution Construction
The probability of selecting an object depends on both the pheromone, which is updated based on the profit of the solutions that are constructed by the object and the heuristics, which depends on the profit and the weight of the object. In the proposed work, the heuristic is calculated as given in (5).
Hi = (VM) * Wc (5)
where, Vi and Wi are the profit and the weight of the object, Wc is the remaining capacity before adding the object. This calculation is similar to the dynamic approach for heuristic calculation.
-
IV. Experimental Results
Although testing cases in most of the recent literature showed that the knapsack problem is easy to solve and can be solved using the exact algorithm in almost pseudopolynomial time, Pisinger [25] “show that the knapsack problem still is hard to solve for these algorithms for a variety of new test problems”.
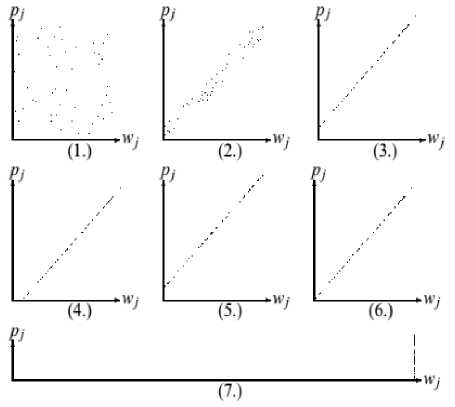
Fig.3. Knapsack Data Categories [25]. (1) Classical Data, (2) Weakly Correlated, (3) Strongly Correlated, (4) Inverse Strongly Correlated, (5) Almost Strongly, (6) Subset Sum, (7) Uncorrelated with Identical Weights.
Accordingly, in order to distinguish the hard knapsack problems from other, the knapsack problems, as illustrated in Fig. 3, were classified into seven categories based on Pisinger [25]. These categories are: 1) classical data, 2) uncorrelated data with identical weight, 3) weakly correlated data, 4) strongly correlated data, 5) subset data, 6) inverse strongly correlated data and 7) almost strongly correlated data. The first three categories are easy to be solved and are used often for testing the knapsack problem’s solution in the literature. The second three categories are difficult to be solved. While the seventh category is very similar to the strongly correlated data, which is difficult to be solved.
In this paper, various datasets from these categories are utilized, with various number of objects. The settings for the experimental results were determined as given in Table 1 for the original and proposed approaches. In the experiments 14 datasets were used, each of which contains 100 problem instances with various number of objects and various item weights and knapsack capacity. Table 2 lists the properties of these datasets.
Table 1. Parameter Settings
|
Parameter |
Value |
Parameter |
Value |
|
Alpha |
1.0 |
Number of Rounds |
1000 |
|
Beta |
1.0 |
Number of Ants |
10 |
|
Evaporation |
0.95 |
Gamma |
0.6 |
Table 2. Summary of the Utilized Datasets
|
Dataset ID |
Type of Data |
# objects |
# instances |
|
Uncorrelated50 |
Uncorrelated |
50 |
100 |
|
Uncorrelated100 |
Uncorrelated |
100 |
100 |
|
WeaklyCor50 |
Weakly Correlated |
50 |
100 |
|
WeaklyCor100 |
Weakly Correlated |
100 |
100 |
|
StrongCor50 |
Strongly Correlated |
50 |
100 |
|
StrongCor100 |
Strongly Correlated |
100 |
100 |
|
InvStrongCor50 |
Inverse Strongly Correlated |
50 |
100 |
|
InvStrongCor100 |
Inverse Strongly Correlated |
100 |
100 |
|
AlmStrongCor50 |
Almost Strongly Correlated |
50 |
100 |
|
AlmStrongCor100 |
Almost Strongly Correlated |
100 |
100 |
|
Subset50 |
Subset Sum |
50 |
100 |
|
Subset100 |
Subset Sum |
100 |
100 |
|
IdnWeight50 |
Uncorrelated/Identical Weight |
50 |
100 |
|
IdnWeight100 |
Uncorrelated/Identical Weight |
100 |
100 |
The experiments are conducted by randomly initialized the pheromones with both the original and the proposed approach. Then, the output profit from the constructed solution is monitored after each cycle. The profits are affected by the pheromones updating process, thus, the better the updating is the faster the optimal profit is reached. Moreover, the number of cycles required to reach the convergence state with the optimal solution is reported.
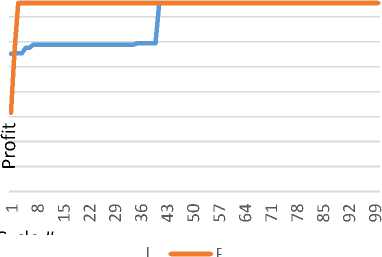
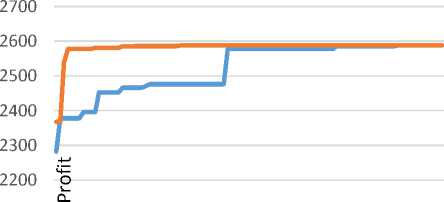
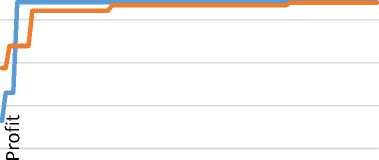
Fig. 4, Fig. 5, Fig. 6, Fig. 7 and Fig. 8 give examples of the results of running the original ACS and the proposed approach over selected instances from “StrongCor50” dataset. The results show that the proposed approach converge faster compared with the original ACS. More specifically, with the rising line of the proposed approach in Fig. 4, for example, it proofs that the proposed approach converges faster, and makes a great enhancement of the gained profit within the first few cycles, compared to the original that makes strong changes after a considerable number of cycles. Even with the instances problems, at which the original approach outperforms the proposed approach, as given in Fig.8, it is noted that the proposed approach makes great changes in the first few cycles, but the original was also fast as well, which prove that the proposed achieved the intended goal.
Proposed
Cycle #
^^^^^^Original
Fig.4. Output Results after each Cycle for Selected Problem 1
mcлLЛг^^mcлLЛг^^mcлLЛг^^ г^г^(^lmm't'tLЛ^£)ю^^cocлcл
Cycle #
^^^^^*Original ^^^^^ Proposed
Fig.5. Output Results after each Cycle for Selected Problem 2
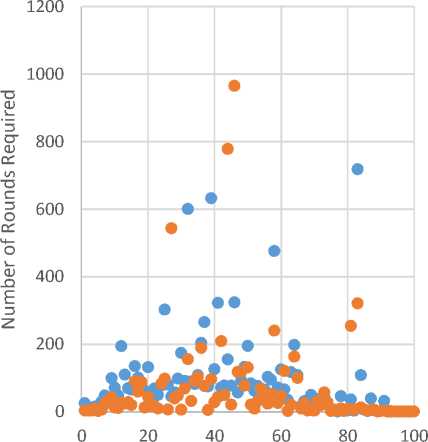
The results of the proposed algorithm, compared with the original ACS, for the 100 problems of the first dataset (Uncorrelated50) are illustrated in Fig. 9. More round comparisons are given in Appendix A. It is noted that the proposed approach requires less number of cycles/rounds to converge compared to the original ACS. The rest of the results, for the other datasets, are summarized in Table 3 and Table 4. As noted, both of the original and proposed finds the optimal solution, with equal accuracy value that is almost 99%. However, the proposed approach is clearly faster than the original one, in most of the problem instances. It is to be noted that the pseudorandom plays a major role in the convergence. Accordingly, with some instance, one of the approaches converge faster not because of the pheromones but because of the randomization process.
As noted in Table 4, the proposed approach sacrifices insignificant accuracy compared with the original one, as the pheromone increment is given to some objects with low profits. However, this reduction in the accuracy is trivial.
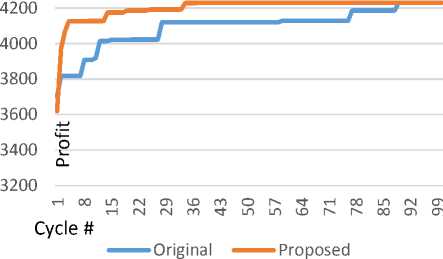
Fig.6. Output Results after each Cycle for Selected Problem 3
Round Comparisons
-
• Original • Proposed
-
Fig.9. Round Comparison of the Original and Proposed Approaches over Uncorrelated50Dataset

oo m Г~ 00
>4 00
Cycle #
Original
Proposed
Fig.7. Output Results after each Cycle for Selected Problem 4
oo m r~ 00
H CO 1Л N СЛ ID н гч гч m
Table 3. Summary of the Results’ Speed
Dataset ID
Average Number of Rounds
Rounds Reduction
Original
Proposed
Uncorrelated50
91.59
65.9
28%
Uncorrelated100
349
322.97
7%
WeaklyCor50
486.65
441.23
9%
WeaklyCor100
596.99
493.94
17%
StrongCor50
388.13
326.78
16%
StrongCor100
523.58
468.3
11%
InvStrongCor50
433.13
391.78
10%
InvStrongCor100
529.87
429.29
19%
AlmStrongCor50
393.52
381.93
3%
AlmStrongCor100
483.95
417.13
14%
Subset50
14.34
10.08
30%
Subset100
4.77
4.24
11%
IdnWeight50
238.28
233.44
2%
IdnWeight100
470.6
447.58
5%
Average
357.4571
316.7564
13%
In summary, the average rate of cycle reduction of the proposed approach compared to the original is 11.4%.
Cycle #
^^^^^^Original
Proposed
-
Fig.8. Output Results after each Cycle for Selected Problem 5
Round Comparisons
Table 4. Summary of the Results’ Accuracy
|
Dataset ID |
Accuracy |
|
|
Original |
Proposed |
|
|
Uncorrelated50 |
100% |
100% |
|
Uncorrelated100 |
99.79% |
99.79% |
|
WeaklyCor50 |
99% |
99% |
|
WeaklyCor100 |
98.36% |
98.36% |
|
StrongCor50 |
99.80% |
99.80% |
|
StrongCor100 |
99.19% |
99.19% |
|
InvStrongCor50 |
98.91% |
98.91% |
|
InvStrongCor100 |
98.46% |
98.46% |
|
AlmStrongCor50 |
99.78% |
99.78% |
|
AlmStrongCor100 |
99.21% |
99.21% |
|
Subset50 |
100% |
100% |
|
Subset100 |
100% |
100% |
|
IdnWeight50 |
99.85% |
99.85% |
|
IdnWeight100 |
99.31% |
99.31% |
|
Average |
99% |
99% |
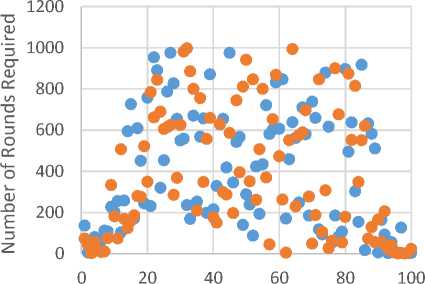
• Original • Proposed
Fig.A.1. Round Comparison for Selected Dataset 1
Round Comparisons
-
V. Conclusion
In this paper, the slow convergence of AC with KP is solved by introducing new heuristics that integrated with the amount of pheromone increase after each cycle. The proposed heuristic integrates the gathered profit so far with the amount of pheromone increment to enforce diversity in the selected items. As such, the amount of pheromone increment at an object increases significantly, if the object is added to a loaded knapsack, while the incremental portion is identical to the original ACS, when the object is added to an empty knapsack. Accordingly, the original ACS treated all objects of a given solution as the same in term of the amount of pheromone increment. On the other hand, in the proposed approach, each object is given different pheromone increment based on the solution profit and the situation of the knapsack before adding the object. The experimental results in seven categories of datasets range from easy to difficult showed that the proposed approach is clearly faster than the original one in most of the problem instances. Nevertheless, with some instances, the original approach seems to converge fast due to the nature of the problem. It is to be noted that the pseudo-random plays a major role in the convergence. Accordingly, with some instance, one of the approaches converge faster not because of the pheromones but because of the randomization process.
Appendix A
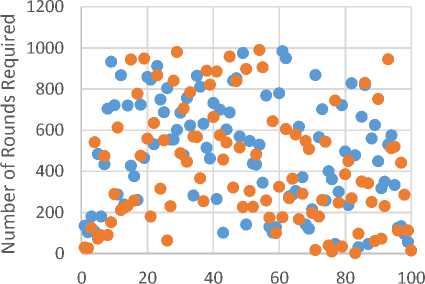
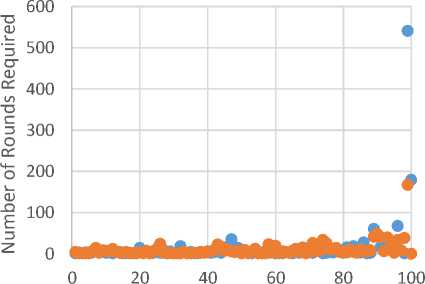
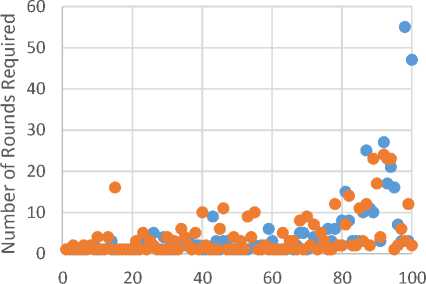
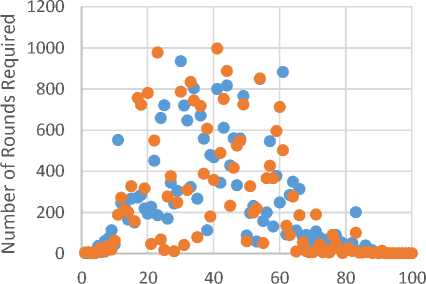
More results are illustrated in Fig. A.1, Fig. A.2, Fig. A.3, Fig. A.4 and Fig. A.5.
• Original • Proposed
Fig.A.2. Round Comparison for Selected Dataset 2
Round Comparisons
• Original • Proposed
Fig.A.3. Round Comparison for Selected Dataset 3
Round Comparisons
Original Proposed
Fig.A.4. Round Comparison for Selected Dataset 4
Round Comparisons
Original Proposed
Fig.A.5. Round Comparison for Selected Dataset 5
Список литературы Ant colony system algorithm with dynamic pheromone updating for 0/1 knapsack problem
- Shareha, A.A.A., M. Rajeswari, and D. Ramachandram, “Textured Renyi Entropy for Image Thresholding”, in Computer Graphics, Imaging and Visualisation, 2008. CGIV'08. Fifth International Conference on. 2008. IEEE.
- Shehab, M., A.T. Khader, and M.A. Al-Betar, “A survey on applications and variants of the cuckoo search algorithm”, Applied Soft Computing, vol. 61, p. 1041-1059, 2017.
- Bazgan, C., H. Hugot, and D. Vanderpooten, “Solving efficiently the 0–1 multi-objective knapsack problem”, Computers & Operations Research, vol. 36, no. 1, p. 260-279, 2009.
- Wang, L., et al., “A human learning optimization algorithm and its application to multi-dimensional knapsack problems”, Applied Soft Computing, vol. 34, p. 736-7432, 015.
- García-Martínez, C., F.J. Rodriguez, and M. Lozano, “Tabu-enhanced iterated greedy algorithm: a case study in the quadratic multiple knapsack problem”, European Journal of Operational Research, vol. 232, no. 3, p. 454-463, 2014.
- Gimadi, E. and I. Rykov. “Efficient Randomized Algorithm for a Vector Subset Problem”, in International Conference on Discrete Optimization and Operations Research. 2016. Springer.
- Jacobson, L. and B. Kanber, Introduction, in Genetic Algorithms in Java Basics. 2015, Springer. p. 1-19.
- Liu, A., et al. “Improved simulated annealing algorithm solving for 0/1 knapsack problem”, in Intelligent Systems Design and Applications, 2006. ISDA'06. Sixth International Conference on. 2006. IEEE.
- Egeblad, J. and D. Pisinger, “Heuristic approaches for the two-and three-dimensional knapsack packing problem”, Computers & Operations Research, vol. 36, no. 4, p. 1026-1049, 2009.
- Thiel, J. and S. Voss, “Some experiences on solving multiconstraint zero-one knapsack problems with genetic algorithms”, INFOR: Information Systems and Operational Research, vol. 32, no. 4, p. 226-242, 1994.
- Hua, Z. and F. Huang, “A variable-grouping based genetic algorithm for large-scale integer programming”, Information Sciences, vol. 176, no. 19, p. 2869-2885, 2006.
- Ye, B., J. Sun, and W.-B. Xu, “Solving the hard knapsack problems with a binary particle swarm approach”, in Computational Intelligence and Bioinformatics, 2006: p. 155-163, Kunming, China.
- Tan, R.R., “Hybrid evolutionary computation for the development of pollution prevention and control strategies”, Journal of Cleaner Production, vol. 15, no. 10, p. 902-906, 2007.
- Zhao, P., P. Zhao, and X. Zhang, “A new ant colony optimization for the knapsack problem”, in Computer-Aided Industrial Design and Conceptual Design, 2006. CAIDCD'06. 7th International Conference on. 2006. IEEE.
- Dorigo, M., M. Birattari, and T. Stutzle, “Ant colony optimization”, IEEE computational intelligence magazine,vol. 1, no. 4, p. 28-39, 2006.
- Sim, K.M. and W.H. Sun, “Ant colony optimization for routing and load-balancing: survey and new directions”, IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, vol. 33, no. 5, p. 560-572, 2003.
- Blum, C., “Ant colony optimization: Introduction and recent trends”, Physics of Life reviews, vol. 2, no. 4, p. 353-373, 2005.
- Dorigo, M., V. Maniezzo, and A. Colorni, “Ant system: optimization by a colony of cooperating agents”, IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 26, no. 1, p. 29-41,1996..
- Bullnheimer, B., R.F. Hartl, and C. Strauss, “A new rank based version of the Ant System”, A computational study, 1997.
- Stützle, T. and H.H. Hoos, “MAX–MIN ant system”, Future generation computer systems, vol. 16, no. 8, p. 889-914, 2000.
- Dorigo, M. and L.M. Gambardella, “Ant colony system: a cooperative learning approach to the traveling salesman problem”, IEEE Transactions on evolutionary computation, vol.1, no. 1, p. 53-66, 1997.
- Zhang, Y.D. and L.N. Wu., “Bankruptcy prediction by genetic ant colony algorithm”, in Advanced Materials Research, 2011.
- Leguizamon, G. and Z. Michalewicz, “A new version of ant system for subset problems”, in Evolutionary Computation, 1999. CEC 99. Proceedings of the 1999 Congress on. 1999. IEEE.
- Schiff, K., “Ant colony optimization algorithm for the 0-1 knapsack problem”, Technical Transaction, Automatic Control, vol. 52, p. 39-52, 2013.
- Pisinger, D., “Where are the hard knapsack problems?” Computers & Operations Research, vol. 32, no. 9, p. 2271-2284, 2005.


