Application of fuzzy logic to assess banks' credit risk

The work of banks is associated with lending activities, investment of funds, and therefore in their activities should take into account the risks of loss of funds. To this end, banks regularly identify significant risks and analyze the causes of their occurrence. To reduce risks, banks make a financial assessment of the situation of individuals and legal entities. Deciding on the basis of which method to build a scoring system that determines the rating is a difficult problem, since the quality of the solution depends both on the model and on the quality of the available data, their noisiness and heterogeneity. The bank evaluates the financial position of the client, first, based on the information available to the bank about the client and, secondly, by requesting additional information on income from the client himself. Further, the data is processed according to its own algorithm adopted in each bank and a customer reliability rating is obtained. The rating is an aggregated assessment of the client's financial position. The rating model for assessing credit risk is quite popular and consists of a set of quantitative and qualitative characteristics of the client. These characteristics are checked, analyzed by the bank and they determine the creditworthiness of the client.

To conduct an adequate analysis of the client's financial position in terms of qualitative characteristics, reliable, from the point of view of the bank, sources of information are used [1]. These are accounting data, data from the tax service, documents received from various departments of the bank. Nowadays, it has become popular to analyze customer data posted on the Internet, media, and social networks.

For quantitative analysis, the data provided by the client in the financial statements is used.

It should be noted that each bank uses its own methodology for calculating the customer's reliability rating and assessing his financial position.

Domain analysis

One of the most popular methods for determining the credit rating based on the summation of points [2]. Quantitative and qualitative characteristics, according to expert judgment, are determined in the form of points. The score based on a rating scale, from highest (good) to lowest (bad). To determine the final indicator of the client's financial position, the arithmetic mean of the points considered based on the sum of all criteria, quantitative and qualitative characteristics.

For example, there is a group of indicators of the bank XXX: quantitative, qualitative and corrective characteristics of the client ( X i ). Each group is characterized by n characteristics.

For each group, the average score of the analyzed group is calculated, and is calculated using the following formula:

average

E ( X 1 + X 2 + X n ) £ X n

where X _average – the average score of the characteristics of the analyzed subgroup; X_n – the analyzed parameter of the characteristics of the subgroup; X ₁ – subgroup indicator; X ₂ – a subgroup indicator.

For each subgroup, the total number of points of quantitative, qualitative parameters and indicators calculated which adjust the client's credit rating. The client's credit rating determined by the formula:

R = ^ X1 average + ^ X2 average + ^ X3 average, where X1average – the average score of the quality parameters of the Client; X2average – the average score of the quantitative parameters of the Client; X3average – the average score of the correcting parameters.

Based on the totality of the assigned points, taking into account the established intervals of the scoring values, the final credit rating of the client (R) and his financial position are determined.

The Table 1 contains a description of the client's financial position in accordance with the rating determined by the parameters of bank XXX.

Table 1

Compliance of the rating with the assessment of financial position

Score Min	Score Max	Rating R	Financial position	Description
0	˂ 1.5	С	not satisfactory	Low degree of creditworthiness. The main indicators of the financial position assessed as satisfactory or close to satisfactory, but their stability is questionable. The company has serious enough problems or is at a significant risk of serious problems
≥ 1.5	˂ 5	В	satisfactory	Average degree of creditworthiness. The financial position assessed as satisfactory and stable in the short term. The company has no problems that could lead to loss of creditworthiness
≥ 5.1	≤ 8	А	high position	High degree of creditworthiness. The financial position assessed as good and stable in the long term. The company has no discernible problems

The aim of the work is to develop fuzzy multi-connected models [3, 4], designed to predict the receipt of a positive or negative decision to receive a banking product, including the assessment of the credit rating of a legal entity (Client).

Modeling method

The use of fuzzy logic methods in credit scoring is not new, it is presented in works [5–8], and however, with the growth of information technologies, new opportunities for their implementation appear. Currently, neural networks and systems with fuzzy logic have proven themselves well in forecasting in the form of a fuzzy neural network [9–12]. The concept of “fuzzy set” fuzzy set, introduced by L. Zadeh in 1965 [13], admits that the characteristic function (the function of membership of an element in a set) can take any values in the interval [0, 1], and not only values 0 or 1. This relation is described using the membership function µ → [0, 1]. L. Zadeh proposed, by analogy with the theory of probability, to use the function [14] as a mathematical model of the linguistic uncertainty of the object [15]:

x е X :[10]. Y = p.(x, B), where Y is the result of calculating the function, expressing the measure of uncertainty (fuzziness) for a specific object x е X; p is a continuous function such that p: X ^ [0, 1]. In essence, the function p determines the distribution of uncertainty on X; X – the domain of definition of the function μ.

The domain of definition specified by an ordered set of values, of an arbitrary nature, called a universal set (or universe).

The support of the function ц ( x , B ) is the subset w с X , on which the function ц ( x , B ) takes on a nonzero value. The set of real numbers usually given as a universal set; B – a vector of function parameters, usually numeric.

Fuzzy inference systems based on rules [16], which can be represented by the following types of production rules, containing in the right-hand sides: three types of production rules, containing in the right parts, can represent constants: constants

R6 :if x1 is X10, x2 is X0, .., xm is Xmm, then y = c0,(1)

fuzzy sets

R6 :if x1 is X0, x2 is X0,.., xm is Xm, then y is Y6,(2)

and linear equations

R6 :if xiis Xi0, x2 isXО,.,xm isXm,(3)

m y6=c о+ Eclx, l=1

where 6 = 1, n, l = 1, m; 6 - is the rule number; n - number of rules; l - number of input; m - number of input variables; c6=(c0,c16,.,cm) - vector of coefficients; X6,Y6 - fuzzy sets characterized by membership functions X^ (xl, dl6), Y6 (y, d6) the shape, size and location of which depends on the vec tors of parameters dl6 и d6.

Fuzzy forecast models are calculated using the formula:

y ⁶= f ( X ⁶ ( k ) , Z i ( k ) e ⁶ ) ,                                                                           (4)

where ԑ i – the vector of parameters and structural elements of the fuzzy i -th model (rules 1, 2, 3).

In this case, the following conditions must be observed [17]:

• 1.    There is at least one rule for each linguistic term of the output variable.

• 2.    For any term of the input variable, there is at least one rule in which this term used as a prerequisite (left side of the rule). Otherwise, there is an incomplete fuzzy rule base.

To predict the bank's decision ( Y j ) to issue a banking product (BP) to the Client, apply fuzzy models like (1)–(3), with parametric and structural learning algorithms and implementing the concept of “soft computing” [18].

Let us introduce the following notation:

Qualitative parameters of the Client X i :

Quantitative indicators of the Client Z i :

Z ( k ) = ( Z 1 ( k ) . Z n ( k ) ) .

The variables defining Y j , respectively: Z j ( k ) = ( Z 1 j ( k ) . Z nj ( k ) ) .

Indicators adjusting the Client's credit rating (ԑ i ):

G ( b ) = ( G 1 ( b ) . G n ( b ) ) and ^accordingly ^G j ( ^b ) = ( ^G 1 j ( ^b ) . ^G nj ( b ) ) .

In addition, it is necessary to take into account the type of banking product (BP) having the number g = 1, N .

Then, according to formula (4), to predict the optimal solution Y j in the b -th bank, fuzzy models of forecasting the optimal solution Y j are required, we obtain the formula:

y g = f ( u g ( k ) , Z g ( k ) G g ( b ) s g ) ,                                                               (5)

g = 1, m, j = n, where m - the number of bank products; n - sample length; sg - a vector of parameters and structural elements of the fuzzy j model.

The accuracy of the forecast is the proximity of the calculated y^g_j to the given Y^g value is estimated by the value of the criterion, which is a function of the error:

J ( ^{s g ( b} ) ) = ^^{s g ( b} ) ) .

Next, you need to check the fuzzy model by the condition:

1 ^N

Ji = 77Я y ( p )^{- y} i p , ^v i = 1, q ,

N s = 1

0 <  J i <  0,2.

In the process of training the model, it is possible to change the number of variables in groups, therefore, to simplify formula (5), we introduce the notation U ( k ) , Z ( k ) and G j ( b ) through X j we obtain formula:

y^g = ^f ( ^ug ( x ij ) , ^Zg ( x j ) ^Gg ( x ij ) ^{s g} ) .                                                               ⁽⁶⁾

Table 2 shows the groups of input variables that influence the decision to provide a banking product ( Y i ).

Table 2

Groups of input variables influencing the decision to provide a banking product

Variable name	Variable label	Categories of Possible Values	Measurement scale
Dependent variables
Y i	Customer not receiving banking products. Receipt of a banking product by a client	0 – bad 1 – good	Nominal
Independent variables
x 1	Principal (client) region	0 – not incl. to the register 1 – incl. to the register	Nominal
x 2	Limit of the banking product of the principal (client) in the given bank	Strong. Good, Satisfactory, Weak	Quantitative
x 3	Number of applications in this bank	Strong. Good, Satisfactory, Weak	Quantitative
x 4	Procurement Law	0 – not incl. to the register 1 – incl. to the register	Nominal
x 5	Principal's form of ownership	0 – not incl. to the register 1 – incl. to the register	Nominal
x j

It should be borne in mind that each bank has individual scoring models [19], in this case we have 39 different models that are built according to these variables. Thus, passing to the new designations of the input variables x i : l = 1, j = 1, q = 39 where q is the number of fuzzy forecast models by formula (4), we obtain y j :

y j = ^f j ( x ij , ^s j ) ^;

R6 : ifx1 (k) is X®, x2 (k) is X^, ., xj (k) is X®, ., xm (k) is Xm; y® (k) = ci0 + c®x1 (k)+. + cijxj (k)+. + cimxm (k), e = 1,n, i = 1,q, where X- fuzzy sets described by membership functions: X(Xj, die), depending on the input variables xj and the parameter vectors e e e e dij = ( dij 1, dij 2,., dij c), where e = 1, n, j = 1, m, i = 1, q; e, ni - number and number of production rules of a fuzzy model predicting the i-th probability indicator yj ; cj - coefficients of linear equations.

The production rules and the fuzzification operation form a fuzzy model [20], which has the following analytical form:

ni

-«1 (k) = S(C) x?(MT)•

= 1

where ( c i ) = ( c ^ , c ®, . , c m ) - vector of coefficients of the linear equation of the 6-th rule;

e = 1,n; Xi (k) = (pe, pex1 (k),..., pexm (k)) - extended input vector of the 6th rule, containing as a multiplier a nonlinear fuzzy function of parameters di

Pe(d®) =

W®

S e= W ^e’

where W ® - the truth value of the 6-th rule, equal to the product of the membership functions.

W0= Xi(X1). Xi( X 2 )... X0( Xm ).

The vector e is refined by the identification algorithm, we indicate parametric (coefficients of linear equations c = {c^}, parameters = {dj},

e = 1, n, j = 1, m, i = 1, q) and structural elements (the number of rules n and the number m and the composition of the variables).

Getting the forecasting valuey_;- (k) , ncheck the accuracy of the forecast and if the value J nj (i) not lower than the permissible value J П = 0.8 and satisfies the condition J П ( i ) >  J П , then we accept.

The structure of a multiply connected fuzzy model is shown in Fig. 1.

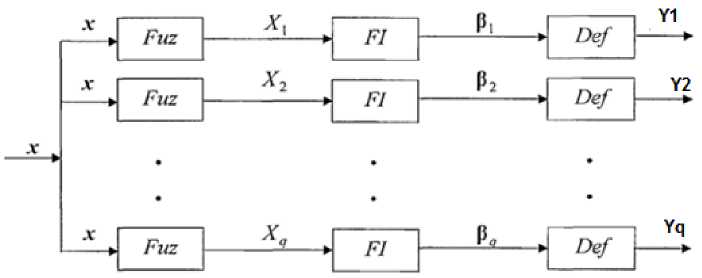
Fig. 1. Structure of a multiply connected fuzzy model

The model is focused on the simultaneous processing of incoming data from many clients and for different banks and different scoring models, so the entire space of incoming data is divided into subspaces using the FCM clustering method. The calculation was performed in the MATLAB system. Fig. 2 shows a fragment of the result of the proposed methodology in a multi-banking system.

Среднее число банков, по которым не прошел скоринг = 3 из 19 Суммарное количество заявок = 2000.0

Количество нераспределенных и отправленных на повтор заяврк= 59 счетчик всех проходов, включая обработку потерянных х = 2059 (' Kb[ 0]=0.01', ' Zbotn[ 0] =0.01027', ' \xf0\xe0\xe7\xed\xe8\xf6\xe0 Kb-Zb^ otn = -O.OOO27') ('КЬ[1]=0.01', ' Zb otn[ l]=0.01253', ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb _п otn = -0.00253’1 ('Kb[2]=0.01', ' Zb otn[ 2] =0.01366',' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.00356') ('Kb[3]=0.01', ' Zb otn[ 3] =0.01002',' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -2e-05’) ('Kb[4]=0.01', ' Zb otn[ 4] =0.01151’, ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb _n otn = -0.00151') (’Kb[5]=0.0r, 'Zb otn[5] =0.01349', ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb Otn =-0.00349') ('Kb[6]=0.01', ' Zb otn[ 6]=0.0111', ’ \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.0011') ('Kb[7]=O.O2', ' Zb otn[ 7] =0.02063',' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.00063') ('Kb[8] =0.03', ' Zb otn[ 8] =0.0292', ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb^ otn = 0.0008') ('Kb[9]=0.04', 'Zb otn[9] =0.04315', ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb Otn =-0.00315') ('Kb[10]=0.05', ' Zb otn[ 10]=0.05174’,' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.00174') (’Kb[ll]=0.06’, ' Zb otnj ll] =0.06469’, ’ \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.00469') ('Kb[12]=0.07', 'Zb otn[ 12] =0.06981', ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = 0.00019') ('Kb[ 13) =0.08', 'Zb otn[ 13] =0.0827', ¹ \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb Otn =-0.0027') ('Kb[14]=0.09', ' Zb otn[ 14]=0.09',' \xfO\xeO\xe7\xed\xe8\xf6\xeO KI>Zb otn = 0.0') (’ Kb[ 151=0.1’, ' Zb otn] 15] =0.10061’,¹ \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = -0.00061') ('Kb[16]=0.12', 'Zb ,otn[ 16] =0.11956’, ' \xfO\xeO\xe7\xed\xe8\xf6\xeO Kb-Zb otn = 0.00044') ('Kb[17]=0.13', ' Zb otn[ 17] =0.13367', ' Vf0\xe0\xe7\xed\xe8\xf6\xe0 Kb-Zb Otn =-0.00367') CKb[18]^0.14^p, ^,Zb_TOtn[18]=0.1199^,_J¹ \xfO\xeO\xe7\xed\xe8\xf5\xeO K^Zb_otn = 0.0201’) »>

• Fig. 2. A fragment of the result of the algorithm

Conclusion

To predict the customer's rel iability rating, three types of fuzzy models we re taken, for certain groups of customer financial indica tors and the requirements of banks. For each mo del, production rules are proposed, membership functions are defined.

The developed mathem a tical model for assessing the client's rating and pred icting the decision to receiv e a banking product based on the fuzzy inference rule made it possible to fin d the most acceptable conclusion. The results obtained were proposed to be used in a multi -banking web-oriented system of providing banking products to corporate clients.