Аналитическое определение температурных полей биополимеров в формующем канале экструдера при коэкструзии

Отдельным сегментом на рынке экструдированных комбикормов являются коэкстру-дированные продукты. Это продукты, состоящие из зерновой оболочки, внутри которой находится начинка (жировая, белковая, витаминная и т.д.). Коэкструдаты являются самыми «молодыми» на отечественном рынке.

Анализ течения термолабильных неньютоновских сред в каналах экструдера требует дополнительной оценки тепловой обстановки, так как неучет диссипативных явлений и не-изотермичности может привести к нежелательным эффектам перегрева и снижению качества готовой продукции.

Рассмотрим экструдер для получения коэкструдированного продукта с расположением жировитаминной начинки внутри зерновой оболочки.

Целью работы является аналитическое определение распределения температурных полей в жировитаминной начинке, которая термо лабильна. В результате декомпозиции каналов по тепловой обстановке выделены следующие участки (рисунок 1): от выхода насоса до корпуса экструдера (I); по толщине корпуса (II); пред-матричная зона (III); коэкструзионная формующая головка (IV). Рассмотрим последовательно теплообмен на всех этих участках.

Теплообмен на участке I можно рассматривать как теплообмен при стационарном движении среды в режиме идеального вытеснения по трубопроводу диаметром 2 мм и длиной 21 мм с температурой среды на выходе, составляющей 60 °С и температурой окружа-ющей среды 20 °С.

Дифференциальное уравнение энергии для стационарного течения с умеренными скоростями в круглой трубе в отсутствие внутренних источников тепла, градиентов концентрации и градиента давления в цилиндрической системе координат ( z , r , О ) таково:

di      di uP— + VP-— dz    dz

1 d( ;t*)

1 rX

r drV  dr J

= 0 ,

где u , v - скорости среды аксиальном направ-лении z и радиальном r соответственно; р , X - плотность и теплопроводность среды; О - угловая координата; t - локальная температура; i - энтальпия среды.

Ограничимся рассмотрением случая течения среды с постоянными физическими свойствами, тогда d i = c p dt, где C p - теплоемкость среды.

В этом случае (1) принимает следующий вид.

dt uP cp — + vP cp dz

d t d r

—

X d f dt) X d21 — — r— + ~2TT2" r dr V dr J r2 d92

= 0,

Следует заметить, что для несжимаемой жидкости уравнение (2) справедливо и без допущения об отсутствии градиента давления.

Далее будем рассматривать гидродинамически стабилизированное и осесимметричное течение ( v = 0, d ² t1 d 9 ² = 0), тогда (2) упрощается:

1 d f d t ) d ² t u d t --I r — 1 + —- = , r d r V d r J d z ² a d z

где a = X pcp - температуропроводность среды.

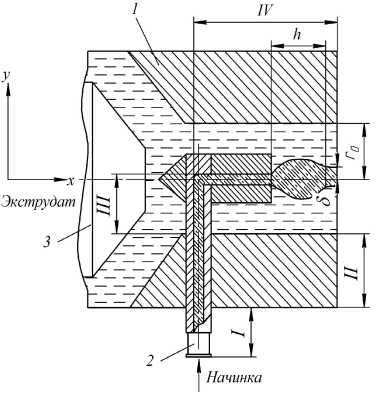
Рисунок 1. Расчетная схема течения экструдата и начинки в формующем канале экструдера: 1 - корпус формующей головки; 2 - подводящий патрубок; 3 - шнек

Без потери точности можно пренебречь аксиальной теплопроводностью по сравнению с радиальной ( d ² 1 /d z ² = 0 ).

ST_L — 1 = Pe ^{— 1}

d ² T_L 1 dT_L

dR ² R dR )

1 5 f 5 1 i u 5 1 -—I r — 1 = -— r d r ( d r ) a d z

dTL ( 0, 5 )

.

dR

= 0;

Для отыскания частного решения уравнения (4) замкнём его граничными условиями

t ( r , 0 ) = t f ;

d t ( 0, z )

d r

t (rp, z ) = t

= 0;

d ² T_L dR ²

T l ( 1, 5 ) = 0, где s , T L – изображение Z и T . После преобразования (17) имеем:

1 dT

+-- L

—

R dR Pe

I T_L + 1 L

Pe

1=0

w ,

Запишем соответствующее однородное уравнение для (20):

где r 0 – радиус канала; t f , t w – температура начин-

ки на входе в экструдер и температура стенки.

В силу предположения идеального течения среды следует, что u = const. Для дальнейшего анализа системы (4)-(7) приведём её к безразмерному виду с учётом того, что t f >  t w , с

d^T L + 1 dT L — ^t_Tl = 0.

dR ² R dR  Pe ^{— 1 L}

Умножим (21-3.79) на R ²:

помощью относительных параметров

R = Д r 0 ; Z = zr ^ ; T = ( t - t w )Д t f - t w ) ;

Pe = ur₀/а к виду:

R 2 <^ + RdT L — dR ²

Пусть:

— S/Pe = ц ²,

S

dR Pe

—

T R T L = 0.

—

, тогда

1 d f _n9 T I   „ d T

R = Pe ;

R d R ( d R )     d z

T ( R , 0 ) = 1;

^ T ^ = 0;

d r

T (1, z ) = 0

R ² d-T^L + R^T L + ц ² r ²t = 0, dR ²     dR ^L

а это есть уравнение Бесселя, которое имеет следующее общее решение:

T l ( R , 5 ) = C 1 1 0

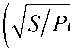
Раскроем слагаемые в левой части уравнения (8):

1 d A d T I 1 fd T _n5 ² T I d ² T  1 d T

R =       + R =    + ;

R d R ( d R ) R (d R d R ² ) d R ² R d R

где I 0 , K 0 – модифицированные функции Бесселя и Ганкеля; С 1 , С 2 – константы интегрирования.

Частные решения неоднородного урав-

нения определяется из соотношения:

At+A

Pe ^{— 1 L} Pe ^{— 1}

= 0,

откуда TL = 1/ S и общее решение уравнения (20) станет:

T l ( R , 5 ) = C 1 1 0 (N Pe^ R ) + C 2 K 0 (# P^R ) + S

С учетом (12) математическая модель теплообмена на участке І примет окончательный вид:

d T = Pe — 1 d Z	f d 2 T 1 d T I + (d R 2 R d R }	;       (13)
T ( R , 0) =	1;	(14)
d T (M= d R	0;	(15)
T (1, z ) = 0 Применим в системе (13)-(16)		(16) интеграль-
ное преобразование Лапласа по переменной Z :

Постоянная С 2 = 0, т. к. при R→0

K 0 ( JsjPeR- -> -^х) , тогда:

T l ( R , 5 ) = C 1 1 „ ( V S/Pe ^{— 1} R ) + S

Константу С 1 определим из условия (19):

T l (1, 5 ) = C , 1 0 (V S/Pe " ' ) + S = 0.

C = -

sI о (7 S Pe -¹ ) ^.

На основании этого решение задачи в изображениях таково:

T l ( R , s ) = S

I о (7 SiPe -' R )

SI о (7 S/Pe - ' ) ' (24)

T ( R , Z ) = 2 X ^{Jо ( р} ” ^К ) exp ( - p n Pe ^{- l} Z ) n = 1 p n ^J 1 ( p n )     ^V ’

Найдем среднюю по сечению температуру:

T ( Z ) = 2 } RT ( R , Z ) dR = 4 X ^exp ( - p n Pe "1 Z ) . о                        n = 1 pn      ^{V               7}

Как видно из (24) для отыскания оригинала соблюдены все условия применения второй теоремы Ващенко-Захарченко. Применим оператор обратного преобразования Лапласа к (24):

L - [ T L ( R , s ) ] = L -

S

- L ^{- 1}

Очевидно, что L ¹

S

I о (7 Sp ^{- 1} R )

sI ₀

(7 SiPe -')

= 1.

Для определения оригинала второго слагаемого введём обозначения:

Ф ( R,s ) = I о (7 S/Pe-¹R ) ; / ( s ) = sI о (7 S/Pe ^-1) .

Найдем корни / ( s ) = G: 1. S = G; 2. и множество корней уравнения:

I ₀

= о,

но I о (7 SlPe -¹ ) = J о ( i^S^e "1 ) , по— этому это уравнение эквивалентно уравнению:

J о ( p ) = о.

Вычислим //( s ) :

/( s )=Iо(TS/Pe7)+s    1 I, se

Определим:

Ф ( R ,о ) = 1; / ' ( о ) = 1; ф ( R , p ) = J о ( p R ) ;

/ ' ( p ) = 2 7 s/^Pe ' 1 1 (7 s/^Pe ' ) = 2 гДрё-¹i -1 1 1 (7 $/^Pe ' ) =

= ^- 2 p iI 1 (7 sJPe ¹ ) =^- 2 p ^J 1 ( p ) .

С учетом формулы обращения:

^ф ( ^{R ,о} )    ” ^ф ( ^R , p n )    / 2_P -1₇\

^{+ X} < exp ( ^- P n ^Pe Z )

/ ( ^о )     n = 1 / ( P n )      ^V ’

получим окончательное решение задачи:

Анализируя полученное решение, можно сделать вывод о том, что на этом участке происходит охлаждение среды. Для получения количественных показателей необходимо определить критерий Pe.

Воспользуемся формулой Дарси:

к P U 2 l

2 d r

где § - коэффициент сопротивления трения; d r = 2 r 0 ; l – длина канала,

В силу высокой вязкости жировой начинки – режим течения ламинарный, поэтому § = 16/Re, где Re - число Рейнольдса

du

Re = ——

p

2 ru

⁰ , тогда:

p

§ = 8 ^ .

r ₀ u

Подставляя (27) в (26), получим:

^ P =

8 p p u ² l _ 2p lu p

r ₀ u 22 r ₀

2 , r ₀ ²

Откуда:

_u = 2 Pr ²

2 p l p

Перепад давления:

∆p = p 1 – p 2 = 7 – 0,1 = 6,9 MПа = 6,9·10⁶ Па; r 0 = 1·10^-3 м; ρ = 886 кг/м³;

μ = 196 Па·с; l = 21·10^-3 м, тогда:

u =

6,9 • Ю⁶- ( 1 • Ю ^{- 3} ) 2

2 • 886 • 21 • 1о ^{- 3} • 196

= 1 • Ю^-3 м / с

Коэффициент температуропроводности равен a = ^ ( p c_p ) , где:

λ = 0,177 Вт/(м·К); ρ = 886 кг/м³; с P =

2303 Дж/(кг·К), тогда:

a = ^о,1 77 = ₈,67 - ю-s _м ² Д

886 • 23о3                 ¹

В итоге: Pe = u^ = ^{1 - 1о} - 3 ^- 1 ^ = 11,53.

а     8.67 -Ю ^{- 8}

Для инженерных расчетов можно применять приближённую формулу:

T ( Z ) « -4 2 exp ( - ц 1 Z / Pe ) M

На выходе из участка І :

Z = 21 • 10 -3/ 1 • 10 ^{- 3} = 21, первый корень уравнения (25) μ = 2,4048, тогда:

T ( Z ) =---- ⁴ -exp I - 2,4048 2^ 1- I = 1,8 •Ю ^{- 5} ;

• ⁷ ( 2,4048 ) 2     I 11,53 )

T ( Z ) = l-w- = 1,8 •Ю^{- 5}; 1 » t _w.

• ^tf - t w

Полученный результат свидетельствует о понижении температуры начинки на участке І, что может привести к забивке канала. Во избежание этого необходимо теплоизоляция канала на участке І. Следует заметить, что полученная математическая модель легко адаптируется и для других участков.

Рассмотрим участок II. В стационарных условиях устанавливается линейный профиль температур по толщине корпуса. Если температура внутренней стенки составляет 150 ºС, а внешней 20 ºС, то средняя температура стенки равна 85 ºС. Расчеты показывают, что в этом случае температура начинки, прошедшая через корпус составляет как раз 85 ºС. Нет смысла в этом случае продолжать последовательные вычисления, ясно, что при заданной геометрии и скорости течения среды, температура начинки на входе в формующий канал превысит допустимую, что приведет к необратимым изменениям в виде разложения жировых составляющих. Для решения этого вопроса необходимо существенное увеличение числа Pe, что может быть достигнуто увеличением скорости или диаметра канала для начинки или одновременно их увеличении.

Таким образом, необходимо решить оптимизационную задачу по выбору режимных и геометрических параметров. Если иметь в виду неизменность конструкционных характеристик экструдера, то решение этой задачи может быть получено следующим образом.

Пусть Pe есть скорость функции начинки, т. e. Pe = Pe ( u ).