Асимметричные модуляции ускорения свободного падения в задаче о свободной конвекции в замкнутой полости
Автор: Мелентьев Анатолий Борисович, Тарунин Евгений Леонидович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 1 (5), 2011 года.
Бесплатный доступ
Методами математического моделирования исследованы эффекты, возникающие при модуляции ускорения свободного падения в случае тепловой конвекция жидкости, подогреваемой снизу. Решалась задача: конвекция в плоской полости квадратного сечения. Модуляция силы тяжести (симметричная и асимметричная) была образована перемещением полости в вертикальном направлении. Выяснено, что отклонение от симметрии колебаний приводит к уменьшению амплитуды колебаний характеристик конвективного течения.
Конвекции, модуляции, асимметрия
Короткий адрес: https://sciup.org/14729712
IDR: 14729712 | УДК: 532.5
Текст научной статьи Асимметричные модуляции ускорения свободного падения в задаче о свободной конвекции в замкнутой полости
Используемая модуляция была вызвана смещением полости в вертикальном направлении по закону y (t) = ’
a cos ^ t ), 0 < t < T ;
- a cos( ® ( t - T )), T < t < T ,
® = n / T , (1)
® 2 = П /(To — T ).
Вторая производная от смещения (1) создавала дополнительное модуляционное ускорение:
y ( t) = g ( t) =
- a®2 cos ^t, 0 < t < T, aw22 cos w2 (t - T), T < t < T.
ции. Эффекты, связанные с влиянием параметра асимметрии, были исследованы в различных задачах [1]. В наших исследованиях фиксированными были параметр асимметрии £ = 2, число Прандтля Pr = 1. Рассматривались случаи как без модуляции (амплитуда смещения и частота модуляций равны нулю), так и с модуляцией: амплитуда смещения а = 0.1, частота модуляции изменялась для поиска резонансных эффектов в интервале от 0 до значения частоты в 2 раза большее, чем частота собственных (без модуляции) затухающих колебаний. Рассматривалась как симметричная модуляция ( £ = 1), так и асимметричная ( £ = 2).
Для решения задачи использовались уравнения конвекции в приближении Буссинеска, решались уравнения двухполевым методом [2, 3]:
Параметрами модуляции являются: а -амплитуда, Т 0 – полный период модуляции и параметр асимметрии £ = ю 1 / ю 2 = (T0 - T ) / T 1 . Значение параметра асимметрии, равное единице, соответствует симметричной модуля-
д^ д ^ д^ д^ д^ „,чд T
— + (^--1—^) = Д^ + Gr (t) —, д t ду дx дx ду дx
^ T ( ^. д T д^ 8 T 1 ,^
д t д у д x д x д у Pr ,
Д^ + ^ = 0,
где у, ю - функция тока и вихрь скорости, Gr(tt) = Gr + Grmod (t) есть сумма постоянной и модуляционной компонент числа Грасхофа. Модуляция ускорения свободного падения входит в модуляционную компоненту числа
Грасхофа:
, П, 2 nt„
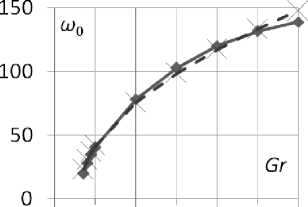
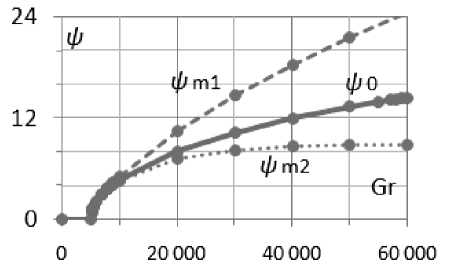
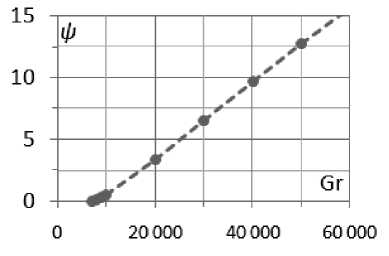
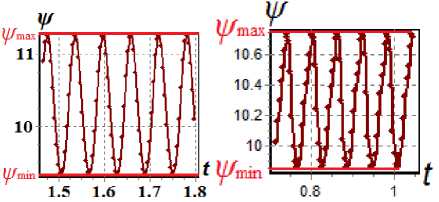
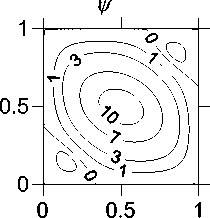
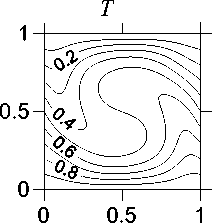
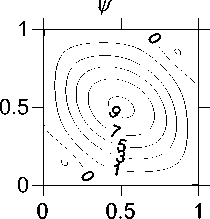
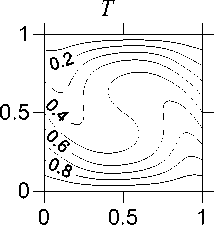
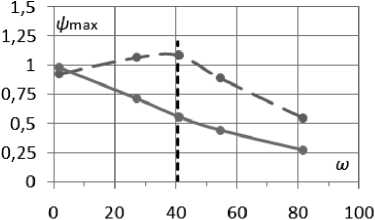
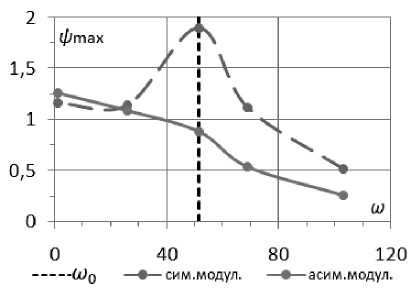
-a(-) cos—,0 Г П .2 п( t - T )T,r a (------) cos------—, T < t < T, [ T - t T - T 10 Уравнения (3) записаны в безразмерных переменных функции тока и вихря скорости. В качестве единиц обезразмеривания расстояния и времени были выбраны размер квадратной полости L и характерное вязкое время ν/L2. Граничные условия соответствовали твердым непроницаемым границам с заданной температурой T Ir = 1 - y. Без модуляции такая задача решалась в работе [1]. 2. Результаты численного решения без модуляций В качестве начального состояния при получении результатов использовалось стационарное решение с возмущение вихря скорости в центре полости ^0 = Ax(1 - x)У(1 - У) • Этому возмущению соответствовало максимальное значение функции тока ^m0 «A-3.3-10-3. В качестве амплитуды возмущений обычно использовалось значение A = 100. Решение системы выполнялось по явной двухслойной схеме с аппроксимацией первых производных конвективных слагаемых центральными разностями. Шаг по времени вычислялся по формуле с запасом, обеспечиваю- щим выполнение условия устойчивости: h2 n 12 + h Уmaxi . Уравнение Пуассона для функции тока решалось на каждом шаге по времени методом последовательной верхней релаксации с оптимальным параметром релаксации [3] до выполнения неравенства max I У^j1 -У^ I i, j i,j i,j < 0.01. (6) Вихрь скорости на границах вычислялся по формуле Тома. Шаг квадратной пространственной сетки равнялся 1/40 (проверочные расчеты выполнялись с шагом 1/60). В процессе счета следили за тем, чтобы сеточное число Рейнольдса [3] не превосходило 2 (это условие необходимо для выполнения условия устойчивости схемы с центральными разностями в конвективных слагаемых). Колебательный характер установления стационарного решения для двух значений числа Грасхофа из интервала 7-103< Gr< Gr^ (61±1)-103 приведен на рис. 1. а б Рис. 1. Зависимость максимума функции тока от времени при а) Gr = 104, б) Gr = 3-104 На рисунках показан способ вычисления периода "собственных" колебаний в процессе установления. Как видно, период этих колебаний уменьшается с ростом числа Грас-хофа. Полученные значения частоты ω0(Gr) представлены на рис. 2. О 20 000 40 000 60 000 Рис. 2. Зависимость ω0(Gr) Методом наименьших квадратов найдена аппроксимационная формула в виде корневой зависимости (пунктирная линия на рис. 2), справедливой для 7-103< Gr< 50-103 с погрешностью не более 20%: Ю (Gr) « 0.6327 Gr - 5621. (7) В вычислительных экспериментах отслеживался процесс установления стационарного режима с погрешностью менее 1%: |ψmn+a1x -ψmnax | |Nun+1-Nun||ωmn+ax1-ωmnax| . (8) |ψmnax| |Nun| |ωmnax| . , где n – номер шага по времени, ψ, ω – максимумы по всей полости функции тока и вихря скорости, Nu – число Нуссельта (отношение интенсивности теплового потока за счёт конвекции к интенсивности теплового потока за счет теплопроводности через всю полость) [2]. Для стационарного решения подкорректирована корневая зависимость максимума функции тока (закон Ландау) от числа Грас-хофа [4]: ψ (Gr) ≈0, 063 Gr-5011 , (9) справедливая c погрешностью не более 4% при 6⋅103< Gr< 58⋅103. Заметим, что число Прандтля в расчетах было равным 1 и потому число Релея равно числу Грасхофа. Зависимость максимума функции тока установившегося течения ψ0 от числа Грасхо-фа на интервале до Gr = 60⋅103 представлена на рис. 3 сплошной линией. Рис. 3. Зависимость ψ(Gr) Штриховые линии определяют характеристики процесса установления. Напомним, что выход на стационарное решение происходил посредством затухающих колебаний. Верхняя линия соответствует первому всплеску максимума функции тока ψm1 (рис. 1, б), а нижняя линия соответствует первому минимуму после первого всплеска ψm2. Как видно, с ростом числа Грасхофа увеличивается размах колебаний установления (ψm1 - ψm2). Рис. 4. Зависимость ψm1 - ψm2 от Gr Для этой зависимости справедлива на интервале 20⋅103< Gr< 60⋅103 формула с погрешностью не более 2%: (ψm1-ψm2) ≈0.00315⋅Gr-2.96. (10) 3. Результаты численного решения с учётом модуляций Перейдем к обсуждению результатов расчета при модуляции согласно формуле (4). Частота модуляций ω соответствует полному периоду модуляции T0 из формул (1) и (2): ω=2π/T . (11) Как при симметричных, так и при асимметричных модуляциях реализуется установившийся режим колебаний. Типичный пример установившегося режима колебаний при значении числа Грасхофа Gr = 3⋅104 и частоты модуляций ω = 51.4 (соответствующей частоте собственных затухающих колебаний ω0) представлен на рис. 5. Рис. 5. Установившиеся колебания при а) симметричной и б) асимметричной модуляции, Gr = 3⋅104, ω = 51.4 В вычислительных экспериментах от- слеживался процесс установления модуляционных колебаний с погрешностью менее 1%: |ψm(na+x1) -ψm(na)x | | Num(na+x1) - Num(na)x | |ψm(na)x | |Num(na)x| < 0.01 (12) , где n – номер колебательного периода (один период – от минимума до следующего мини- мума), ψ , Nu – максимум функции тока по всей полости и числа Нуссельта через полость за один период колебания. На рис. 6 и 7 представлены изолинии функции тока и температуры в момент максимума и минимума значений функции тока при симметричных модуляционных колебаниях, изображенных на рис. 5,а. Рис. 6. Картина течения при максимальном значении функции тока колебательного режима при симметричной модуляции, Gr = 3⋅104 Рис. 7. Картина течения при минимальном значении функции тока колебательного режима при симметричной модуляции, Gr = 3⋅104 На рис. 8 и 9 представлены зависимости амплитуды функции тока, как разности максимального и минимального значений, от частоты модуляции ω при Gr = 104 и Gr = 3⋅104. На рис. 8 и 9 ω0 – это частота собственных колебаний без модуляции, полученная на рис. 2. -----Uq —♦—сим.модул. —♦—асим.модул. Рис. 8. Амплитудная кривая для Gr = 104 Рис. 9. Амплитудная кривая для Gr = 3⋅104 Как видно из рис. 8 и 9, симметричные модуляции с частотой, равной частоте собственных колебаний ω0, приводят к резонансу (прерывистая линия), однако при асимметричных модуляциях такого эффекта резонанса не наблюдается (сплошная линия), что аналогично результатам, полученным в механической задаче [1]. Представленные выше результаты соответствовали интервалу чисел Грасхофа от Gr1 = (5.5±0.5)⋅103 до Gr ≈ (61±1)⋅103. При значениях числа Грасхофа Gr > Gr ≈ (61±1)⋅103 процесс установления собственных затухающих колебаний без модуляций приводил, как и в [3, 4], к регулярным колебаниям. Исследование этой области значений числа Грасхофа планируется в дальнейшем. Выводы 1. Найдены зависимости характеристик колебательного режима установления стационарного решения (частоты и амплитуд) в области чисел Грасхофа, где существует стационарное решение в отсутствии модуляции. 2. Показано, что при модуляции в области рассмотренных чисел Грасхофа реализуется установившийся колебательный режим с частотой модуляции как для симметричной, так и для асимметричной модуляции. 3. Найдена зависимость амплитуды колебаний, вызванных модуляцией для симметричной и асимметричной модуляции. Показано наличие резонансного эффекта модуляции в случае симметричной модуляции.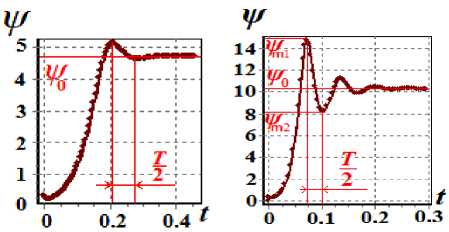
Список литературы Асимметричные модуляции ускорения свободного падения в задаче о свободной конвекции в замкнутой полости
- Тарунин Е.Л. Обзор особенностей асимметричных колебаний//Проблемы механики и управления. Нелинейные динамические системы/Перм. ун-т. Пермь, 2005. №37. С.169-187.
- Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972. С.242-255.
- Тарунин Е.Л. Вычислительный эксперимент в задаче свободной конвекции: учеб. пособие/Иркутск. ун-т. Иркутск, 1990. 228 с.
- Гершуни Г.З., Жуховицкий Е.М., Тарунин Е.Л. Численное исследование конвекции жидкости, подогреваемой снизу//Известия АН СССР. Механика жидкости и газа. 1966, №6.


