Асимптотика решения задачи Дирихле с сингулярностью внутри кольца

DOI:

Исследуем краевую задачу Дирихле еАи(р, ф, е) - (р - с)2nu(р, ф, е) = fр, ф, е), (р, ф) е D,

и ( a , ф , е ) = 0, и ( b , ф , е ) = 0,

,    д ²     1 д 1 д ²

где А = —_у + -—+ -у—у др ² р др р ² дф ²

- оператор Лапласа в полярной системе координат; 0 <  е <<

1 –

малый параметр; n е N , D = {( р , ф ) | a <  р <  b , 0 <  ф <  2 п }, 0 <  a <  c <  b - const;

+x f (р, ф, е)= ^е* fk (р, ф), f(С, ф, 0) * 0, fk(р, ф) е C”(DиГ), Г - граница области D. к=0

Известно [2], что решение задачи Дирихле (1)-(2) существует и единственно при 0 <  е -const. Требуется построить асимптотическое разложение решения задачи (1)-(2) при е ^ 0.

Не нарушая общности, считаем, что граничные условия (2) однородные, так как неоднородные граничные условия и ( a , ф , е ) = Ф 1 ( ф , е ), и ( b , ф , е ) = ^ ₂( ф , е ), ( ф 1 ₂( ф , е ) - бесконечно дифференцируемые функции) с помощью линейного преобразования и ( р , ф , е ) = v ( р , ф , е ) + + ( ^ ₂( ф , е ) ( р - a ) + Ф 1 ( ф , е ) ( b - р )) / ( b - a ), относительно р , всегда можно привести к однородным v ( a , ф , е ) = 0, v ( b , ф , е ) = 0.

В бисингулярно возмущенных задачах одна особенность связана с сингулярной зависимостью решения от малого параметра, а другая – с негладкостью членов асимптотики [3]. В работах [3; 8–11] методом сращивания построены асимптотические разложения решения различных сингулярно возмущенных эллиптических уравнений. А в работах [1; 4–6], используя данную ме- тодику, построены полные асимптотические разложения решения задачи Дирихле с особенностями на границах области. В данной работе доказывается применимость обобщенного метода пограничных функций для решения задачи Дирихле в случае, когда вторая особенность появляется внутри области.

Уравнение (1) является бисингулярно возмущенным. Первая сингулярность – решение предельного уравнения не может удовлетворять граничным условиям (2). Вторая особенность (сингулярность) – коэффициенты ее внешнего разложения имеют нарастающие особенности, когда р >  с , то есть внешнее разложение имеет вид

U ( р,ф,s ) = X^s ku^k ( р,ф ) , при s >  0,                              (3)

к = 0

где и о ( р , ф ) = - f , ( р , ф ) / ( р - с ) ² n , U k ( р , ф ) = -(f k ( р , ф ) — A U k _ч( р , ф )) / ( р - с ) ² n , к е N , U k ( р , ф ) = = O ( ( р- c )^{- 2} n ^{- (2} n ^{+ 2) k} ) , k = 0, 1, 2, ... при р >  с .

Заметим, что асимптотический ряд (3) теряет свойство асимптотичности при | р - с\ < s ^1/(2 n ⁺²⁾ .

Докажем следующую теорему.

Теорема. Для решения задачи (1)-(2), при s >  0, справедливо асимптотическое разложение и ( р , ф , s ) = V ( р , ф , s ) + W ( т , ф , ц ) + Q ( П 1 , ф , X ) + Q ( p ₂, ф , X ),                 (4)

где      V (р, ф, s)=£s kvk (р, ф),      W (т, ф, ц) = f> kwk (т, ф),     Q (П1, ф, x)= XXk^k (П1, ф), k=0                                 k=-2 n                                 k=0

Q ⁽ n 2 , ф , ^{X )} = X ^{х k} ~ k ⁽ П 2 , ф ) , т = ( р - с ) / ц , s = ц ² n ⁺² , р, = ( b - р )/ X , р, = ( р - а ) / X , s = X ² , причем k = 0⁰

V k ( р , ф ) е C ” ( D и Г), W k ( т , ф ) е C ” ( D 0 ), Q k ( П 1 , ф ) е C ” ( D 1 ), q_k ( п 2 , ф ) ^{е С} °( D 2 ) , D j = {( П j , ф )| 0 <  П j < <+ * , 0 <  ф < 2 п }, D 0 = {( т , ф )| | т |<+ да , 0 <  ф < 2 п }, q_k ( ^ 2 , ф ) = O ( е ^{-П 2} ) , q_k ( р 1 , ф ) = O ( е ^{-П 1} ) , k = 0, 1,..., ^при П 1,2 >  + ^ ; ^w ( k -1)(2 n +2)+2+ j ^{( т} , ф ) = ^{0 ( т -2} n j j = 0, 1,-, ² n ^-1; w k (2 n +2) ^{( т} , ф ) = ^{O ( т -(} 2 n + ^{2) )}, w k (2 n +2)+1 ^{( т} , ф ) = O ( т ^{-(2 n +1)} ), k = 0, 1, .... , | т | >  + да .

Доказательство. Доказательство теоремы состоит из двух частей: построение формального асимптотического разложения решения (ФАРР) задачи (1)–(2) и обоснование этого ФАРР, то есть оценки остаточного члена.

Построение ФАРР . Для построения ФАРР задачи (1)–(2) применяем обобщенный метод пограничных функций. ФАРР задачи (1)–(2) будем искать в виде (4). Учитывая граничные условия (2), имеем:

Q (0, ф , X ) = ф 1 ( ф , X ² ), ф 1 ( ф , s ) = - V ( b , ф , s ) - W (( b - с ) / ц , ф , s ),               (5)

Q) (0, ф , X ) = ф ₂( ф , X ² ), ф ₂( ф , s ) = - V ( а , ф , s ) - W (( а - с ) / ц , ф , s ).

Подставляя (4) в (1), получим:

sA V ( р , ф , s ) - ( р - c ) ^{2 n} V ( р , ф , s ) = f ( р , ф , s ) - h ( р , ф , s ), ( р , ф ) е D ,

ц

2 n

:sW

^ С/ т

L5 W   .    5 2 W -т 2 n W )

a + тц дт ( а + тц ) ² дф ²         J

= h ⁽тц, ф, ц ^{2 n + 2} ) ( т , ф )

е D ₀,

д ² Q X д Q др ² b - P 1 X др 1

^{+ X} . v ^QQ ^{- ( b - c - n} 1 ^{X) 2} n ^Q = 0,^{( n} 1 , ф ) ^е D 1 , ( b - p 1 X ) дф

~

д2 Q + X д Q + X2 д2 Q дп2 a + H2X дП2  (a + n2X)2 дф2

X д Q

^{— (} c ^— a ^— П 2 ^х) 2 n Q ~ = 0, ( П ₂, Ф ) e D ₂,

где W = W ( т , ф , ц ), Q = Q ( n 1 , Ф , X ), Q = Q ( n ₂, Ф , X ).

По идее метода, ввели вспомогательный асимптотический ряд в виде функции to h (p, Ф, s)= 2 s khk (p, Ф), которую конкретизируем ниже.

k = 0

+®

Учитывая V ( p , ф , s ) = 2 s k v_k ( p , ф ) , из соотношения (7) для функции v k ( p , ф ) имеем:

k = 0

^v 0 ⁽ p , Ф ) = ^- f ) ⁽ p , Ф ) ^- h 0 ⁽ p , Ф )) / ⁽ p ^- c ^{) 2} n ,

V k ( P , Ф ) = -(f k ( P , Ф ) - A v_k -1 ( р , ф ) - h_k ( p , Ф )) / ( p - c)² n , k e N .

Пусть gk(p, Ф) = fk(p, Ф) - AVk-i(p, Ф), k = 0, 1,., v-i(p, Ф) = 0, тогда Vk(p, Ф) e C(to)(D), k = 0, 1, …, когда hk (p, Ф) = 2 gk, j (Ф)(P — c)j, gk, j (Ф) = д gk (^ ф) | p=c, k = 0, 1, . . j=0                                  j !дpj

Отсюда получаем vk(p,Ф) = — 2gk,j№ — c)j 2n, gk,j(Ф)=д gk 'p'ф)|p=c, k = 0, 1, . . j=2 n                                  j!^p J

+to

Таким образом, мы определили все члены асимптотического ряда V ( p , ф , s ) = 2 s ^kv_k ( p , ф )

k = 0

в области ( D и Г).

Из (8) для функции w k ( т , ф ) имеем:

+to

2 цk+2 n k=—2 n

P ² w k ^(т, ^ф) t дт ²

—

^т 2 n w n ^(т, Ф ) =

+to

— 2 ц k+22

k =— 2 n

дwk (т, ф)

Ц        + ц^ дт

2 ^{д 2} w k ( т , ф )

дф ²

+2

+to2 n —1                     ,      .

+ 2 2 g k , j ( ф ) т ² ц ^{7 +| 2 n + 2 )} k .

k = 0 j = 0

Для функций w k ( т , ф ) ставим следующее предельное условие:

w k ( т , ф ) ^ 0, при т ^ ± to , k = -2 n , -2 n + 1, ... .

Получаем следующие задачи:

д ² w

^Lw — 2 n =----

2 n ^(т, Ф )

дт ²

—

^{т 2 n}w — 2 n ^(т,^ф) = g 0,0 ^(ф) , w _{-2 n} ( т , ф ) ^ 0, при т ^ ± да ,

Lw -2 n + j = g 0j• ⁽ Ф ^{) т} j ^{- Ф} -2 n + j ^{( т} , Ф ), w -2 n +j ^{( т ,} Ф ) ^ ⁰, при ^т ^ ± ^да , ^j = 1, ², ., ² n ^- 1,

Lw k (2 n +2)+ 5 = ^{- Ф} k (2 n +2)+ 5 ^{( т} , Ф ), w k (2 n +2)+ 5 ^{( т} , Ф ) ^ ⁰, при ^т ^ ± ^to , ⁵ = ^{0,1 k} = ⁰, 1, . ,

Lw k (2 n +2)+2+ j = g k+1,,j ^{( ф ) т} j ^{- Ф} k (2 n +2)+2+ j ^{( т} , ^{ф )}, w k (2 n +2)+2+ j ^{( т} , ^{ф )} ^ ⁰, при ^т ^ ± ” , j = 0, 1, …, 2 n – 1; k = 0, 1, …,

. ( a d w_k _i( t , ф) d ² w_k_ ₂(t , ф)

где Ф k ( t , ф ) =    k ¹      + ^k„4 .

дт         дф ²

Докажем следующие вспомогательные леммы.

Лемма 1. Пусть f(T)f2(ф)C”(D0). Тогда задача д z(т, ф) -т2nz(т, ф)= f_(t)f2 (ф),    (т, Ф)е D0

дт имеет единственное решение z(т, ф)е C"(D0) в классе функций, растущих не быстрее какой-либо степени т, когда т ^ ±да.

Доказательство . Пусть т = ^{n + y} n '+ 1 t и z ( t , ф ) = z 1 ( T ) f ( ф ), тогда получим

z[(t)-(n +1)2/(n+1)(n +1)2n/(n+1)t2nz 1 (t) = (n +1)2/(n+1)f1 (n +1n+1t),     t e R, или zf(t)- (n +1)2t2(n+1)-2z1 (t) = (n +1)2/(n+1) f1 (n +Уn+Tt)     t e R .

Фундаментальная система решений соответствующего однородного уравнения z‘'(t)-(n +1)212(n+1)-2 z1(t ) = 0

имеет вид ^{ U ₂₍ n +1) ⁽ t ), U 2( n +1) ^(- t )}, где U 2 ( n + 1 ) ( t ) = ^ K 1/2 ( n + 1 )⁽ t n ⁺ 1 ) , t > 0, K 1/2( n +1) – функция Макдональда [7]. Приведем некоторые свойства фундаментальной системы решений { U _{2( n +1)}( t ), U 2( n +1) (– t )}:

• а)    Вронскиан этих решений равен

W ( U 2( n +1) ( t ), U 2( n +1) (- 1 )) = 2( n + 1)cosec( n / (2 n + 2);

• б)    при t = 0 имеем

  - n /(2 n+2)   /    ,    \                    7-( n+2)/(2 n+2)/

1 \

2 n + 2 J ^;

U2(n+1)(0) =-----rl I, U'2(n+1) (0) =-------prl -

V П V 2 n + 2 У

• в)    при t ^- + да функция U ₂ ( _{n +1} ) ( t ) экспоненциально убывает: U ₂( _{n + 1}) ( t ) ~ t ^{n /2} e t ;

• г)    при t < ^{0: U} 2 ( n + 1 )⁽ t ) = ^й ^_л cos ec 2 ( n ^K+ 1 ) I 1/ ( 2 n + 2 )⁽ t n ^{+ 1 )+} K 1/ ( 2 n + 2 )⁽ t n + 1 ^)J, где I 1/( ₂ n +2) (№ +1 ) ^-

• функция Бесселя мнимого аргумента;

• д)    при     t ^ - да     функция     U ₂ ( _{n +1} ) ( t )    экспоненциально растет:

U 2 ( n + 1 ) ( t ) = cos ec 2( ^ + 1) 1 1 1 ^{- n /2} e t" ^{+ 1 (}1 + O ⁽ 1 1 ^{-( n + 1 )} )) .

С помощью фундаментальной системы решений { U _{2( n +1)} ( t ), U _{2( n +1)} (– t )} мы можем записать явное решение неоднородного уравнения (15):

^{z (} t , Ф ) = f 2 ( ^ ) c^U 2 ( n + 1 ) ^{( t} ) J ^U 2 ( n + 1 )^(- S ) f 1 ⁽ n + ^{1 n} + ¹S^dis +

-да

⁺ f 2 ^) c^U 2 ( n + 1 )^(- t ) J ^U 2 ( n + 1 )^{( s} ) f 1 ( n ^ y n + T ^s ) d^s , t = ^T / n + У Й + Т.

t

С помощью этой леммы мы можем записать явные, единственные решения задач (11)–(14):

w -2n

(        t

+to

^{( t} ) J ^Z 1 ⁽ s ) d^S

t

^{( t} , Ф ) =- g 0,0 ⁽ Ф ^{) с} z i ^{( t} )J z 2 ( 5 ) d^S + z 2

V     -to w-2n + j (t, ф) = CZ1(t) J (g0, j (Ф)S j - Ф-2n+j (s, T))z2 (s)ds +

-to

⁺ cz 2 ^{( t} ) J ⁽ g o, j ⁽ Ф ) s j ^-ф - 2 n + j ⁽ s , Ф )к ⁽ s ) ds , j = i²,-.,² n ^- 1;

t

W k ( 2n + 2 ) + m ^{( t}, ф ) = CZ 1 ^{( t} ) J ^Ф k ( 2 n + 2 ) + m ⁽ S , Ф ) Z 2 ⁽ S ) dS ⁺ CZ 2 ^{( t} ) J ^Ф k ( 2 n + 2 ) + m ⁽ S , Ф ) Z 1 ⁽ S ) dS , m = 0,1; -to                                               t

W2k(n+1)+2+j (t, ф) = CZ11 t) JФ2k(n+1)+2+j (S, ф)Z2 (S)dS + CZ2 1 t) J Ф2k(n+1)+2+j (S, ф)Zi(S)dS, j = 0, 1, … , 2n – 1; k = 0, 1, … , где z 1(t) = U2(n+1)(t), z2(t) = U2(n+1)(-1), t = т/n +1 n +1, c = 2(n + 1)cosec(n / (2n + 2) ^ 0.

Лемма 2. Решение уравнения y"(x) - x2ny(x) = xk, n e N, k e Z, x e R разлагается в асимптотический ряд

У (x ) = xk - 2 n 2a jx-2(n+1)j, x >■/

• j=0

при этом ряд (17) можно многократно почленно дифференцировать и он является ФАР решения уравнения (16).

Доказательство . Подставляя асимптотический ряд (17) в (16), имеем:

2 a j ( k - 2 n - 2 ( n +1 ) j )( k - 2 n - 2 ( n +1 ) j -1 ) x^{k - 2 n - 2 ( n + 1 ) j - 2} - 2 a j x k ^{- 2 ( n + 1 ) j} = x^k .

j = 0                                                                            j = 0

И здесь однозначно определяем коэффициенты a . :

a ₀= -1, a 1 = -( k- 2 n )( k- 2 n -1), a j ₊₁ = ( k - 2 n - 2( n + 1) j' )( k - 2 n - 2( n + 1) j' - 1) a j , j = 1, 2, 3, .„

Оценим теперь остаточный член ряда (17). Пусть r(x) = y(x) – ym(x), где m ym (x ) = xk -2 • 2a,x - 2 n+1)j.

j = 0

Тогда для r ( x ) получим уравнение:

r " ( x ) - x ^{2 n} r ( x ) = O ( x ^{k 2 n}"

(2( n +1) m +2) ).

Уравнение (18) имеет двухпараметрическое семейство решений r ( x , C ₁, C ₂). Из этих решений выберем то решение, которое удовлетворяет условиям: r (- to ) = r (+ to ) = 0:

/          , \     /        t                      +to          A

r(t) = O(tk-2n-2(n+1)m-2) z(t) jZ2(s)dS + z2(t) JZ1 (s)dS I, V     -to                   t         J где z 1(t) = U2(n+1)(t), z2(t) = U2(n+1)(-t), t = x /n +1 n +1, c = 2(n + 1)cosec(n / (2n + 2) * 0.

Учитывая асимптотические свойства в) и д) функции U _{2( n +1)} ( t ), получаем:

r ( t ) = о ( t t- ^{2 n -(2( n +1)} m ^{+2)-2 n} ) = о ( t t- ^{2 n -2( n +1)(} m ⁺¹⁾ ), при t ^ ± _да .

Отсюда имеем: r ( х ) = O ( х ^{к- 2 n -2( n +1)(} m ⁺¹⁾ ), при х ^ ± ^ .

Применяя лемму 2, при т ^ ± ^ мы для функции W j ( т , ф ) получаем следующие асимптотические оценки:

w k(2 n +2)+2+ j ( т , ф ) = о ( т ^{2 n +} ' ), j = 0, 1,..., 2 n -1; к = -1,0,.

w k(2 n +2)+ m ^{( т} , ф ) = ^{0 ( т —(2 n +2)+} m ), m = 0,¹; ^к = 0, ¹ ...

То есть V k , w_k ( т , ф ) ^ 0 при т ^ ± ^ , к = -2 n , -2 n + 1, ... . Отметим также, что при е ^ 0 справедливы разложения:

W | — V Ц

+^

b - c

Ц

+^

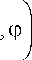
= 1 ^{е k}w к ( ф ) , к = 0

|                  к

,ф,ц| = 1 ц Wk

У к =- 2 n

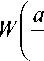
ц

c

-, ф, ц

v к | a1 Ц W I -к=-2 n      V

+ ^

—, ф| = 1е к~к (ф).

^ц У к = 0

А из соотношения (9) при Q ( п₁ , ф , Х ) = 1 Х^_к ( п₁ , ф ) для функции q_k ( п ₁, ф ) имеем: к = 0

у^»|д 2 »к <Л1, ф)

\

+^

к = 0

2 n

V дп2

k

—

а ² ” q_t ( П 1 , ф ) = 1 х ^{к + 1}

д qk (П1, ф)

—

У

к = 0 <

дП 1

+^      2 n

_х к + 2 д ² q k ( П 1 , ф )

\

+ 1^1 C*2. (- 1Ул1«2"—,qt —, (П1, ф)+ 1 Х‘1 Ci, (— 1)jnja

к = 0   j = 0

к = 2 n + 1    j = 0

дф ²

2 n - j

+

У qk - j (П1, ф),

где а = b - c .

Учитывая условие (2), имеем q 2 к (0, ф) = V1, к (ф), q 2 к+1(0, ф) = 0, к=0,1,2, . , дополнительно требуем, чтобы qk(п 1, ф) ^ 0, при П1 ^ +да, к = 0, 1, 2, . . Отсюда lq0 _д q0(п1,ф)-а2nq0(П1,ф) = о, q0(0, ф) = ^ю(ф), lim q0(П1,ф) = 0,         (19)

дп ₁                                        ’ П 1 ^+”

lq_t = :!( - 1 ) ' П 1 ' С j ,а ^{2 n - l}q_t - j ( n 1 , ф ) ₊ ^{д q} 4 ^— 1 ( П 12 ф ) - ^{д 2 qk 2} (р ¹ - ф ) , 1 <  к < n j = 1                                       ^дП 1             дф ²

lq . = 1 ( -D j n ' C . j ,а ^{2 n -} jq_t_' ( П 1 , ф ) +З ^ Ч^- ^{д 2 qk} - ² < ^{П 1} - ^ф) , к >  n j = 1                                     ^дП 1             дф ²

'Ф1,m Ы при к = 2m lim qk (П1, ф) = 0, к = 1, 2, .

П 1 ^+^

0, при к = 2 m + 1, m g N

Так как уравнение у " ( x ) - к ² у = F ( x ), 0 <  x <  да с краевыми условиями у (0) = у ⁰ , у (+ да ) = 0 имеет единственное решение:

1 ( x                   x                   +да                 Л

У (x) = у 0e-kx + — J ek(x-s)F(s)ds - J ek(s -x)F (s)ds + J e-k(x+s)F (s)ds 2 k U            0             0            J, то задачи (19), (20) тоже имеют единственные решения, и при п ^ +да для решения этих задач имеем:

qо (П1, ф)=^1,о(ф)e П1 , q2к+1(П1,ф)=e П1    X njq2к+1,j (ф), j=1

n           n 4k q2к (П1, Ф) = Ф1,к (Ф)e П1 + e П1 Xnjq2к, j (ф), j=1

где q_k j ( ф ) - ограниченные, гладкие функции.

Следовательно,

Q ( р_ь ф, X ) = e ^{П 1 а} n

Л +да      ,                           х +да

X х2к к, к (Ф)+P2 к (п 1, ф)) + X х2к+1P2 к+1 (п 1, Ф) к к=0                              к=0

4 к                                  4 к + 2

где P2к(П1,Ф)=Хп1^2к,j(Ф) P2к+1(П1,ф) = X njq2к+1,j(Ф) j =1

Проведя аналогичное исследование, для решения задачи (7)–(3) получаем:

~ ( П 2 , Ф, X ) = e ^п 2 ^а n

+да+да

X Xк (v2,к (Ф) + P2к (П2, ф)) + X Xк+1P2к+1 (П2, ф) к к=0                               к=0

а= c - a .

Таким образом, мы построили ФАРР (4). Перейдем теперь к обоснованию этого ФАРР.

Обоснование ФАРР . Пусть

R(р, ф, е) = и(р, ф, е) - us(р, ф, е), где s                   2 s+1                                      (2 n+2) s+1

us(р, Ф,е) = Xеkvk(р,ф)+ X хк(qk(п1,ф)+~к(п2,ф))+ X   ^kwk(т,ф), к=0              к=0                                 к=-2 n

R ( р , ф , е ) - остаточный член.

Тогда для R ( р , ф , е ) получим задачу:

еA R ( р , ф , е ) - ( р - c ) ^{2 n} R ( р , ф , е ) = О ( е s ⁺¹ ), е ^ 0, ( р , ф ) е D , R ( a , ф , е ) = O ( e ^-Ш), R ( b , ф , е ) = O ( e ^-Ш), 0 <  X ^ 0,

Применяя преобразование [1; 4-6] и принцип максимума, получаем оценку R ( р , ф , е ) = O ( е ^s ), е ^ 0, в области D и Г. Следовательно, справедливо асимптотическое разложение (4), то есть теорема доказана.

Заключение

Построено равномерное асимптотическое разложение по малому параметру е, решения краевой задачи Дирихле для бисингулярно возмущенного линейного неоднородного дифференциаль- ного уравнения в частных производных эллиптического типа второго порядка с двумя независимыми переменными в кольце. В рассматриваемом случае предельное уравнение имеет вторую особенность внутри кольца, и для этого случая мы доказали применимость обобщенного метода пограничных функций. Методом сращивания тоже можно построить асимптотическое разложение решения исследованной задачи Дирихле, но, на наш взгляд, примененный подход значительно сокращает вычисления. Полученный асимптотический ряд представляет собой ряд Пюйзо. Главный член асимптотического разложения решения имеет отрицательную дробную степень по малому параметру, что свойственно бисингулярно возмущенным уравнениям. Формальное асимптотическое разложение решения задачи Дирихле обосновано принципом максимума.