Assessing Different Crossover Operators for Travelling Salesman Problem

Published Online October 2015 in MECS

Different evolutionary techniques [1-3] have been proposed in literature to solve complex optimization problems. These techniques differ in implementation, but, all of them have very similar formalization of the problem. They start by an initial population of candidate solutions and then apply nature-inspired variation and selection mechanism on select candidate solutions to produce new solutions (offspring), in an iterative fashion. The process is repeated unless some stopping criteria are met. The central idea is that the solutions with better fitness value (according to a given fitness function) will guide the search process towards the optimal solution in the search space. The sketch of an evolutionary algorithm is depicted in Fig. 1.

At the heart of these algorithms is a crossover operator which introduces variation in the population in a systematic way. The crossover operator is stochastic (i.e., probabilistic based) which merges information from two or more parents to produce one or more offspring. Crossover serves two complementary search abilities: exploitation and exploration. That is, it provides new points for further testing upon hyper planes already represented in the population (exploitation), and it also introduces representatives of new hyper planes into the population (exploration).

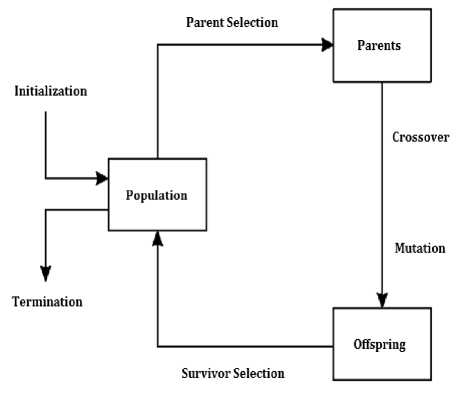
Fig.1. Schematic diagram of an evolutionary algorithm

In literature, different crossover operators have been proposed: Two-Point Crossover (TPX) [4], Partially Mapped Crossover (PMX) [5], Cycle Crossover (CX) [6], Shuffle Crossover (SX) [7], Edge Recombination Crossover (ERX) [8], Uniform Order-based Crossover (UOX) [9], Sub-tour Exchange Crossover (SEX) [10], and Sequential Constructive Crossover (SCX) [11]. These operators have primarily been designed to solve one of the most widely studied optimization problem, Traveling Salesman Problem (TSP), however, they can be adapted to solve other complex optimization problems as well, e.g. scheduling problem.

In this study, the above-mentioned crossover operators are empirically evaluated against four benchmark instances of travelling salesman problem, two symmetric and two asymmetric instances.

The rest of this article is organized as follows. In Section 2, we give a background overview of different crossover operators. The evaluation criteria and test problems are described in Section 3. The empirical study is outlined in Section 4, followed by discussion in Section 5. The article concludes in Section 6.

• II.    Background and Related Work

Different crossover operators have been proposed in literature on evolutionary algorithms, and different studies have been conducted to evaluate the performance of these operators. In [15], the authors compared ten different crossover operators on numerical optimization problems. The select crossover operators are used in genetic algorithms with binary representation. They found that both uniform crossover and reduced surrogate crossover offer competitive performance. In another study [16] , the authors compared the performance of eight different crossover operators on vehicle routing problem. They reported that the best performance was achieved by combining the different crossover operators, whereas the individual performance of the different operators was not good enough to solve the vehicle routing problem. In [17], the authors proposed three crossover operators, namely GA-like one-point, sub-tree, and semantic aware sub-tree, for postfix genetic programming. They evaluated the performance of these on select real-valued symbolic regression problems. They found that the semantic aware sub-tree crossover is best among the three crossover operators.

In what follows, we review the most commonly used crossover operators to solve TSP.

• A.    Two-point Crossover

Two-Point Crossover (TPX) is a typical form of n-point crossover proposed by De Jong [4]. In TPX, two crossover points are pseudo-randomly selected at the same position from each parent chromosome. The parent chromosomes are then split at the crossover points chosen and all data beyond the two select points in either chromosomes is swapped between the two parent chromosomes effectively yielding two offspring.

• B.    Partially Mapped Crossover

Partially Mapped Crossover (PMX) [5] is a two-point crossover. However, unlike the standard two-point crossover as described above, PMX yields one offspring as follows. Two crossover points are selected at the same position from each parent chromosome, and then in a first step the genes are copied from the second parent between the two cut points to the offspring. Then, in a second step, the remaining genes in the offspring before and after the cut point are copied from the first parent in the order in which they appear therein. In case, a gene has already been provided by the second parent (in the first step), the corresponding (i.e. mapped) genes are copied from the first parent, hence the term partially mapped.

• C.    Cycle Crossover

Cycle Crossover (CX) [6] generates offspring by first identifying cycles between two parent chromosomes, and then these cycles are copied from the respective parent chromosomes to form offspring. At the heart of CX is a cycle formation method which works as follows. It starts with the first gene of the first parent, visits the gene at the same position of the second parent, and then goes to the position with the same gene in the first parent, effectively forming a cycle. The same process is repeated to form the remaining cycles. Finally, the indices that form a cycle are used to produce offspring in alternating order.

• D.    Shuffle Crossover

Shuffle Crossover (SX) [7] is a variant of one-point crossover in which, first, the genes are pseudo-randomly shuffled in the parents before applying the crossover. Then after recombination, the genes are shuffled back in reverse order, in the offspring.

• E.    Edge Recombination Crossover

Edge Recombination Crossover (ERX) [8] operator starts by constructing an edge map from nodes which lists all the incoming and outgoing connections for two parents. If a node appears twice, it is marked negative to signify a common edge. This edge map is subsequently used to generate offspring in such a way that the parent structure be preserved as much as possible. The nodes having negative values or with the fewest remaining adjacent nodes are selected before the nodes with more adjacent nodes.

• F.    Uniform Order-based Crossover

Uniform Order-based Crossover (UOX) [9] is different than other crossover operators as it uses a uniform crossover mask (0s and 1s) to construct offspring. In a first cycle, the operator copies genes from the first parent in the slots where the mask has a 1. Then in a second cycle, the remaining genes are copied in the order they appear in the second parent to complete the empty slots in the offspring.

• G.    Sub-tour Exchange Crossover

Sub-tour Exchange Crossover (SEX) developed by Yamamura [10] is used to solve a problem with vary huge data like TSP. It starts by identifying sub-tours including common nodes in both parents. Then, it constructs offspring by copying parents' paths and exchanging the subtours. This crossover operator tends to preserve parent structure by inheriting edges from parents.

• H.    Sequential Constructive Crossover

The Sequential Constructive Crossover (SCX) [11] operator constructs an offspring from a pair of parents using better edges in the parents. SCX also uses the better edges even if they are not in the parents’ structure, which permits it to introduce new and good edges to the offspring. The SCX operator works as follows. It starts with the first node, say s, in the first parent and searches sequentially through each parent to find a legitimate node (not visited yet) in each parent. Suppose the nodes x and y are found as legitimate nodes, the operator constructs a new edge (s, x) if distance(s, x) < distance(s, y), otherwise the new edge (s, y) is constructed. The process is repeated until the offspring is completed. Since the operator preserves the good edges from each parent and also introduces some better edges, it guides the search towards an optimal solution.

• III.    Performance Measure and Evaluation Benchmark

  Different evaluation measures have been suggested in literature to measure the performance of an evolutionary algorithm. In this study, solution quality expressed in terms of cost-minimization is considered the only performance measure. The performance of the select crossover operators was evaluated against one of the most widely studied optimization problem, TSP. TSP is an NP-hard combinatorial optimization problem, in which a salesman has to visit N cities (nodes) by starting the trip from a given city and returning back to the starting city to complete a tour . The constraint is that each and every city should be visited, and it should be visited exactly once. The objective is to find a minimum length tour, which captures resemblance of different real life costminimization problems like spreading a wide-area network. Two types of TSP problems are generally studied: Symmetric TSP and Asymmetric TSP. In a symmetric TSP, the distance between two node x and y is the same as the distance between y and x , whereas in an asymmetric TSP the distance between two node x and y may be different than the distance between y and x . Four benchmark instances of TSP were solved, two symmetric and two asymmetric. The two symmetric instances were ST70 (70 cities) and TSP225 (225 cities), the asymmetric instances were FTV100 (100 cities) and FTV170 (170 cities) [15]. The best known solutions for these problem instances are: 675, 3919, 1788, 2755, respectively [18].

• IV.    The Experiment

• A.    Experimental Setup

  We implemented the system in Matlab-R2009a to run the simulations on a Sony Vaio Core i5-2430M, with 2.4 GHz speed and 4 GB RAM (DDR3). A brief description of this implementation is outlined below.

• •    The solutions were encoded as permutation vectors, where the length of a solution (tour) was the number of nodes in the respective problem instance.

• •    The fitness function was tour length realized as distance between the adjacent cities; the objective was to find the minimum cost tour.

• •    Initial population was sampled randomly; the population size was kept 100 throughout the study.

• •    Parent selection was realized probabilistically as

roulette wheel indexes to calculate probabilities as inverse distances divided by sum of inverse distances (of all candidate solutions in the current population).

• •    Crossover and mutation probabilities were kept 0.8 and 0.01 [19], respectively, throughout this study.

• •    An elitism based survivor selection was implemented, which guarantees that the best solutions from the current generation carry over to the next generation, unaltered.

• •    The maximum number of generations were kept 50000 throughout the study.

In each generation, best and average fitness of population were recorded, similar in spirit to [20], for each crossover operator.

• B.    Results and Analysis

The simulation results in terms of solution quality and speed were recorded for the competing crossover operators on the select problem. We measured the quality of a solution in terms of percentage surplus error value as shown in Equation 1, where optimal value is the known global optimum.

( solution value-optimal value ⁾

=                         ∗100    (1)

optimal value

An ANOVA test was also administered to test whether the apparent differences in the performance gain are statistically significant or not. Table 1 shows the solutionquality results averaged over 20 independent runs, including the overall best solution (Best), the mean of best-of-run solution averaged over 20 runs (Mean), and the standard deviation in best-of-run solution (Std Dev). The results indicate that overall the Sequential Constructive Crossover (SCX) outperformed all other crossover operators, with Edge Recombination Crossover (ERX) offering worst performance. These results are also evident from Fig. 2 and Fig. 3, which depict the evolutions of solutions TSP-70 cities and TSP-100 cities instances, respectively. An ANOVA analysis further revealed that the solution-quality results differed significantly across different crossover operators for the four select problem instances: F (7, 31) = 2.94, F-critical = 2.42, p < 0.05.

Table 2 shows the execution time to complete 50000 generations, again, averaged over 20 independent runs. The results indicate that TPX (Two-point Crossover) completes the required number of generations much faster than the other operators, while ERX (Edge Recombination Crossover) being the slowest one; these results are also evident in Fig. 4. Again, the ANOVA analysis showed that the CPU-time results differed significantly across different crossover operators: F (7, 31) = 8.47, F-critical = 2.39, p < 0.05.

Table 1. Solution quality (percentage surplus error)

Crossover Operator	ST70		FTV100		FTV170		TSP225
	Mean (Std Dev)	Best	Mean (Std Dev)	Best	Mean (Std Dev)	Best	Mean (Std Dev)	Best
TPX	13.79% (1.62)	12.58%	63.82% (3.19)	57.09%	81.08% (11.89)	77.38%	101.76% (15.06)	98.27%
PMX	22.94% (7.26)	20.71%	130.35% (9.02)	127.38%	143.27% (19.16)	127.38%	196.27% (21.35)	192.81%
CX	14.68% (3.19)	12.37%	111.76% (5.32)	108.92%	132.03% (11.74)	128.46%	207.81% (18.11)	203.63%
SX	57.37% (8.92)	54.61%	189.28% (15.03)	182.78%	211.75% (19.56)	206.92%	245.21% (23.95)	239.13%
ERX	66. 21% (7.01)	63.18%	203.06% (13.85)	197.49%	258.04% (19.74)	249.17%	311.11% (29.17)	307.04%
UOX	14.96% (2.78)	13.62%	73.06% (4.19)	71.85%	105.86% (11.97)	102.06%	123.92% (14.82)	118.04%
SEX	16.97% (2.73)	13.58	107.36% (13.18)	103.04%	141.28% (20.96)	137.29%	177.08% (16.28)	173.96%
SCX	2.05% (0.32)	1.74%	14.17% (2.06)	11.97%	34.85% (10.49)	29.72%	45.91% (7.59)	42.97%

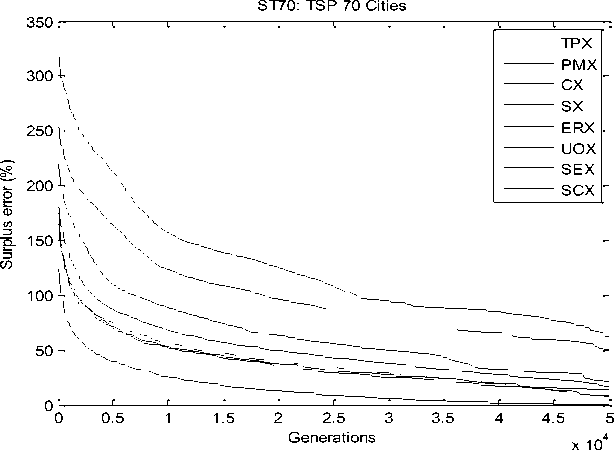
Fig.2. Convergence graph of different crossover operators for TSP-70 cities (symmetric) instance

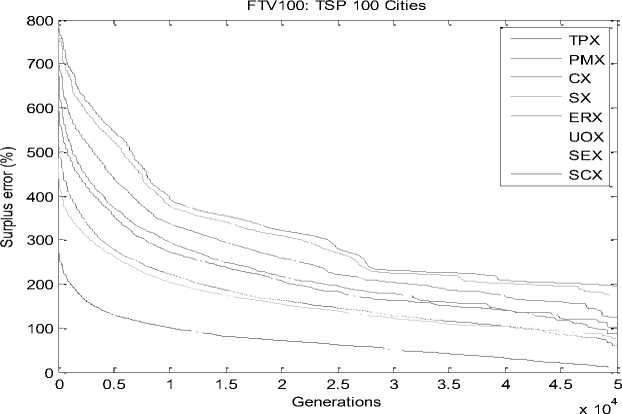
Fig.3. Convergence graph of different crossover operators for TSP-100 cities (asymmetric) instance

Table 2. Mean computational time (seconds) to complete 50000 generations

	ST70	FTV100	FTV170	TSP225
Operator	Mean	Mean	Mean	Mean
	(Std Dev)	(Std Dev)	(Std Dev)	(Std Dev)
TPX	328.91	405.83	653.78	1196.25
	(31.07)	(38.41)	(47.29)	(84.26)
PMX	1186.33	2109.27	5362.29	7109.47
	(180.17)	(173.04)	(276.68)	(418.05)
CX	1073.31	1338.24	2271.05	3691.85
	(131.09)	(146.72)	(163.51)	(274.38)
SX	3591.04	5219.85	7091.57	9591.58
	(219.17)	(527.18)	(318.39)	(612.32)
ERX	7073.18	9401.88	12038.73	16024.51
	(624.11)	(716.06)	(961.01)	(1143.85)
UOX	2392.02	7206.35	9701.18	10851.53
	(144.96)	(412.13)	(367.18)	(1063.71)
SEX	1207.28	1733.94	2174.95	3485.02
	(139.37)	(148.81)	(219.74)	(619.47)
SCX	1403.97	1907.58	2693.08	4106.18
	(97.25)	(154.81)	(172.37)	(394.75)

— ♦ — ST70 — ■ — FTV100  —*— FTV170     TSP225

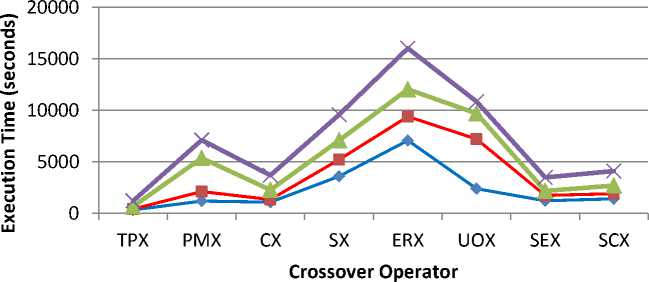
Fig.4. Average execution time of different crossover operators to complete 50000 generations

• V.    Discussion

In the present study, the performance of different crossover operators was evaluated against two dimensions: solution quality and execution time. The study revealed some interesting results.

• •    First, even though not a single crossover operator was able to find the best known solution for the four select TSP instances (the best known solutions: ST70 = 675, TSP225 = 3919, FTV100 = 1788, FTV170 = 2755) [15], overall, Sequential Constructive Crossover (SCX) offered the best performance: on each test problem, the surplus error was marginally above the best known solution as compared to other operators. Interestingly enough, SCX also offered competitive performance in execution time, even though not the fastest one.

• •    Second, Edge Recombination Crossover (ERX) is very slow because of its complex nature, involving lots of computations to construct edge maps. One might expect that this sophisticated and complex

computation benefit in attaining a good quality solution, however, the results suggest otherwise. ERX is found both the slowest in speed and worst in solution quality. Interestingly, Two-Point Crossover (TPX) was observed as the fastest operator. This may be because TPX is relatively simple, it just finds two crossover points, split along those points and glue parts alternating between parents.

When the number of cities is small (e.g., ST70), the performance of different crossover operators is much better as compared to large number of cities (e.g., FTV170). To this end, we combined the results of relatively smaller number of cities ST70 and FTV100, and the results of relatively larger number of cities FTV170 and TSP225, for both solution quality and computational time. The ANOVA analysis on these combined results revealed that the results differed significantly between small and large problems: (Solution quality: F(1, 7) = 2.95, F-critical = 2.13, p < 0.05; Time: F(1, 7) = 7.06, F-critical = 2.68, p < 0.05). This may be interpreted as the different crossover operators evaluated in this study are not that much scalable and their performance may degrade when the problem complexity increases.

• •    Another interesting result came to fore during the analysis of results. The select crossover operators can be clustered into three different groups based on solution quality: SCX in one group, with the best overall performance, TPX and SX in another group, with the worst overall performance and PMX, CX, ERX, UOX and SEX in yet another group, with medium performance. These results are evident from Fig. 2 and Fig. 3. ANOVA analysis further revealed that the difference between three clusters are highly significant: F(2, 11) = 6.91, F-critical = 4.26, p < 0.01.

• •    Finally, it was expected, before analysis of the results, that the solution quality of the different crossover operators would be better for symmetric problems as compared to asymmetric problems. However, the results indicate that there is no significant difference among these crossover operators for symmetric and asymmetric problems: F(1, 7) = 0.85, F-critical = 4.06, p = 0.47.

• VI. Conclusion

In this study, eight different crossover operators were evaluated empirically against two instances of travelling salesman problem (TSP-29 city and TSP-70 city). The select crossover operators were implemented to build an experimental setup upon which simulations were run. The performance of these operators was analyzed in terms of solution quality and computational cost. It was found that SCX outperformed other operators in attaining 'good' quality solution, whereas TPX outperformed other operators in terms of computational cost. Moreover, the select crossover operators can be clustered into three different groups based on solution quality: SCX in one group, with the best overall performance, TPX and SX in another group, with the worst overall performance and PMX, CX, ERX, UOX and SEX in yet another group, with medium performance.

The present study also revealed that the performance of different crossover operators is much better for relatively small number of cities (e.g. 70 cities), both in terms of solution quality and computational time. However, the performance of these operators deteriorated when the number of cities were relatively large (e.g. 170 cities). This raises an interesting question on the scalability of these crossover operators. We conjecture that the performance of these operators may degrade when the problem complexity increases. Interestingly, we did not observe any significant difference on the performance of the select crossover operators for symmetric and asymmetric TSP problems, meaning that they perform equally good on both symmetric and asymmetric problems.