Автокодировщик электрической активности головного мозга человека

Развитие современных междисциплинарных подходов на стыке информационных технологий и физиологии привело к появлению большого числа устройств коммуникации между человеком и компьютером, таких как интерфейсы «мозг–компьютер», окулографических, миографических интерфейсов. Подобные перспективные направления рассмотрены в работах [1–4]. Разрабатываемые устройства коммуникации человека и машины планируется использовать для решения широкого спектра задач, связанных с реабилитацией пациентов неврологического и травматологического профилей, совершенствованием управления различными устройствами: от домашнего компьютера до авиационных систем [5, 6]. Наиболее распространённые задачи, решаемые в настоящее время – это улучшение их аппаратной части, разработка новых алгоритмов обработки полученных сигналов и дальнейшей трансформации их в команды на устройства-эффекторы, поиск новых физиологических феноменов, которые можно использовать как основу для команд, передаваемых по новым интерфейсам [7, 8].

Данная статья посвящена решению задачи сжатия электрической активности головного мозга человека, регистрируемой с помощью электроэнцефалографии (ЭЭГ) с целью получения модели искусственной нейронной сети, способной сжимать первичную информацию с минимальными потерями и воссоздавать исходное состояние с определенной степенью качества, что необходимо для задач машинного обучения и задач машинной классификации.

Цель исследования заключается в разработке метода сжатия ЭЭГ, содержащего полезный сигнал в виде вызванного потенциала (ВП), с последующим восстановлением и сохранением возможности выделения ВП с сохранением его свойств.

Мещеряков Р.В., Вольф Д.А., Автокодировщик электрической активности Туровский Я.А. головного мозга человека

Пусть имеется единичный экземпляр данных электрической активности головного мозга человека, представляющий собой вектор x ( x е M m ) . Требуется получить вектор z размерностью p : p ( x е R p , p <  m) - такой, что можно было бы восстановить x . Более того, на основе z можно оценить (описать) x .

Несмотря на широкую распространённость, существующие алгоритмы обладают следующими недостатками:

• 1.    С одной стороны, на первый взгляд может показаться, что задача достаточно простая и действительно существуют различные алгоритмы компрессии данных, которые бы с легкостью из x получили бы z . Однако, например, применяя ту же элементарную компрессию на базе XOR или используя более мощные алгоритмы типа PPM, LZSS и т. д., по результатам работы данных алгоритмов достаточно сложно будет сказать что-то про x .

• 2.    С другой стороны, данную задачу можно решить с помощью алгоритмов, базирующихся на SVD, понизив размерность пространства ^m до размерности нового пространства ^p , в котором располагается вектор z . Тогда возникает резонный вопрос: насколько минимальным должно быть p , чтобы максимально подробно сказать что-то про x ?

Новизна данного исследования исходит из решения самой задачи сжатия: m -мерный вектор в виде некоторого признака (полученного на основе прикладных данных – электроэнцефалограммы – ЭЭГ), ассоциированного с образцом x (т. е. x ∈ ^m ), с помощью искусственной нейронной сети кодируется в p -мерный вектор z (т. е. z ∈ ^p ); применяя глубокое машинное обучение, находится функция кодирования z = ф (x ), такая, что может быть выполнено декодирование x = ^ ( z ).

1.    Теоретические аспекты автокодирования данных искусственной нейронной сетью. Проблематика.

Автокодировщик (АК) – это разновидность искусственной нейронной сети, целью которой является восстановление входной информации (данных) на выходе. АК выполняет всего две задачи: 1) сжатие входных данных в представление скрытого пространства (или латентного вектора), также известное как информационно узкое место; 2) восстановление выходных данных на основе полученного представления. Сам по себе процесс автокодирования – это неконтролируемый алгоритм машинного обучения, так как алгоритм извлечения признаков определяется в результате глубокого машинного обучения.

Понятие информационно узкого места (англ. Information Bottleneck – IB) было введено Tishby и др. [9]. Данное понятие было представлено вместе с гипотезой о том, что IB может извлекать релевантную информацию, сжимая объем информации, которая проходит через всю нейронную сеть, используя предварительно изученное сжатие входных данных.

Традиционно АК использовались в задачах понижения размерности для изучения информативных признаков. И только относительно недавно АК-модели со скрытыми параметрами, которые используют концепцию априорного и апостериорного распределения, такие как вариационные АК, начали использоваться для построения генеративных моделей, которые могут генерировать новые данные. Это достигается за счет сжатия информации в информационно узком месте таким образом, что из всего набора данных извлекаются только важные признаки, и эти извлеченные признаки (представления) могут использоваться для создания новых данных.

С формальной точки зрения, математическая модель АК может быть выражена следующим образом:

ϕ :χ → F

ψ:F → χ                                     ₍₁₎

9,V = argmin^^ ||х - ^ ° ^||2, где ϕ – функция кодера; X – исходные данные; F – скрытое пространство; ψ – функция декодера.

По сути, нейронная сеть разделяется на два сегмента: кодер и декодер.

Функция кодировщика, обозначенная ϕ , отображает исходные данные X в скрытое пространство F , которое присутствует в IB. Функция декодера, обозначенная ψ , отображает скрытое

Математика

пространство F в IB на выходе. Выход в этом случае совпадает с входной функцией. Таким образом, воссоздается исходное изображение после некоторого обобщенного нелинейного сжатия.

Сеть кодирования может быть представлена стандартной функцией нейронной сети, пропущенной через функцию активации, где z – скрытая размерность:

z = о (Wx+b).(2)

Аналогично сеть декодирования может быть представлена таким же образом, но с другим весом и смещением – b, и потенциально используемыми функциями активации:

x' = о'( WZ+b').(3)

Используя (2) и (3), функция потерь примет вид:

(x,x') = |x-x'||2 =|x-cr'(W'(ct(Wx + b)) + b')|| .(4)

Функция потерь (4) используется для обучения нейронной сети с помощью стандартной процедуры обратного распространения ошибки.

Ввиду того, что вход и выход – это одни и те же данные и, как уже было обозначено выше, что алгоритм машинного обучения АК является неконтролируемым, процесс глубокого машинного обучения АК является самоконтролируемым обучением. Цель самоконтролируемого обучения АК состоит в подборе таких функций кодировщика и декодера, чтобы размерность IB была минимальной для кодирования входного сигнала, но достаточной для его восстановления на выходе.

При достаточно небольшом числе персептронов в слое IB способность воссоздавать входную информацию на выходе будет ограниченным и сильно отличаться от оригинала (высокие потери). Если используется слишком большое количество персептронов, то вообще нет смысла использовать сжатие, АК может начать выполнять задачу по реконструкции исходного сигнала (в проводимом исследовании это отрицательный эффект), не извлекая полезной информации о распределении данных, если:

• –    размерность скрытого представления совпадает с размерностью входа;

• –    размерность скрытого представления больше, чем размерность входа;

• –    для АК предоставляется слишком большой объем данных.

2.    Экспериментальное проектирование модели автокодировщика ЭЭГ сигналов

В этих случаях даже линейный кодер и линейный декодер просто копируют входные данные на выход, не изучая ничего полезного о распределении.

Обобщая изложенные выше теоретические аспекты, можно заключить, что в сети АК, функционально левая часть является кодирующей частью, а правая часть – декодирующей. В идеале можно организовать любую архитектуру АК, задавая размеры IB на основе сложности моделируемого распределения.

Поэтому целью глубокого машинного обучения АК является не копирование входных данных на выходе нейронной сети, а обучение АК восстановлению входных данные таким образом, чтобы информативно узкое место выделяло (как бы узнавало) только полезную информацию.

На сегодняшний день применение АК активно популяризируется в задачах реконструкции изображений и их базовой раскраски, сжатия данных, преобразования изображений в оттенках серого в цветные изображения, создания изображений с более высоким разрешением и т. д. Однако проблема заключается в том, что различные модели АК работают только с данными, которые аналогичны тем, на которых они были обучены, это прикладные данные.

Учитывая приведенные выше теоретические аспекты, был разработан специальный АК для кодирования ЭЭГ-данных. Для получения модели АК использовались прикладные данные, которые представляют собой структурированные записи электрической активности головного мозга человека в результате проведенного эксперимента с устойчиво зрительно вызванным потенциалам (УЗВП, англ. Steady state visually evoked potentials – SSVEP – зрительные вызванные потенциалы устойчивого состояния) – это сигналы, которые головной мозг генерирует в ответ на визуальную стимуляцию с постоянным периодом воздействия.

Когда сетчатка глаза возбуждается вспышками частотой от 3,5 до 75 Гц, мозг генерирует электрическую активность с частотой мигания вспышки [10, 11]. Данный потенциал нашел ши-

Мещеряков Р.В., Вольф Д.А., Автокодировщик электрической активности Туровский Я.А. головного мозга человека рокое применение в задачах разработки и дальнейшей модификации интерфейса «мозг– компьютер» как один из хорошо выявляемых, воспроизводимых и не требующих в большинстве случаев специальной подготовки оператора, феноменов мозговой активности [12–14]. Первичной задачей эксперимента было формирование базы данных с ЭЭГ УЗВП от 30 испытуемых обоих полов в возрасте от 17 до 23 лет (12 девушек и 18 юношей), не имеющих неврологических и психиатрических патологий. Перед экспериментом участники не принимали психотропных препаратов и имели нормальное или скорректированное до нормального зрение. Данные электроэнцефалограммы фиксировались прибором «Нейрон-спектр-4ВП» (ООО «Нейрософт», Россия) на отведениях O 1, O 2, Oz , P 3, P 4 и Pz с частотой дискретизации 5 000 Гц, включенным режектор-ным фильтром и отключенным фильтром высоких и низких частот. Фотостимуляция осуществлялась c частотами 1, 8 и 14 Гц. Длительность каждого сеанса УЗВП составляла 15 с.

С целью создания обучающего массива данных для последующего получения модели АК, способного работать с ЭЭГ-информацией, предварительно была проведена работа по их обработке. В первую очередь произведена фильтрация электроэнцефалограмм полосным фильтром Баттерворта 6-го порядка (order) с пропусканием 2 (lowcut) – 35 (highcut) Гц. Далее сигналы были сгруппированы по частотам фотостимуляции (1, 8 и 14 Гц) и группам отведений « O 1», « O 2», « Oz », « P 3», « P 4», « Pz » для каждого испытуемого. С учетом частоты дискретизации после группировки были получены три матрицы с данными:

N = 30× M = 75000× V = 6 элементов, где:

N – порядковый номер испытуемого;

M – количество семплов в сигнале;

V – количество сигналов в группе по каждому испытуемому (также пусть данная величина обозначает множество, состоящее из {« O 1», « O 2», « Oz », « P 3», « P 4», « Pz »}).

Несложно заметить, что имеются достаточно большие наборы по M для множества V . Для снижения размерности V произведено ресемплирование каждого сигнала в группах до M = 25 000 с сохранением структуры данных.

Аугментация данных осуществлена за счет «разбивки» признака M на окна по 1260 отсчетов с шагом 625 отсчетов. В сумме для каждого отведения получено по 1140 образцов для последующего глубокого машинного обучения АК.

Итоговая архитектура модели полученного АК – «кодер–декодер» – представляет собой симметричный многослойный мульти-адаптивный нейрон прямого распространения [15–17]. Кодировщик позволяет отобразить признаки размерностью 1260 элементов в признаки размерностью 24 элемента. Однако данная размерность была получена не сразу. Релевантность полученных признаков также оценивалась с помощью глубокой нейронной сети в части декодера, который позволяет реконструировать исходный сигнал (рис. 1).

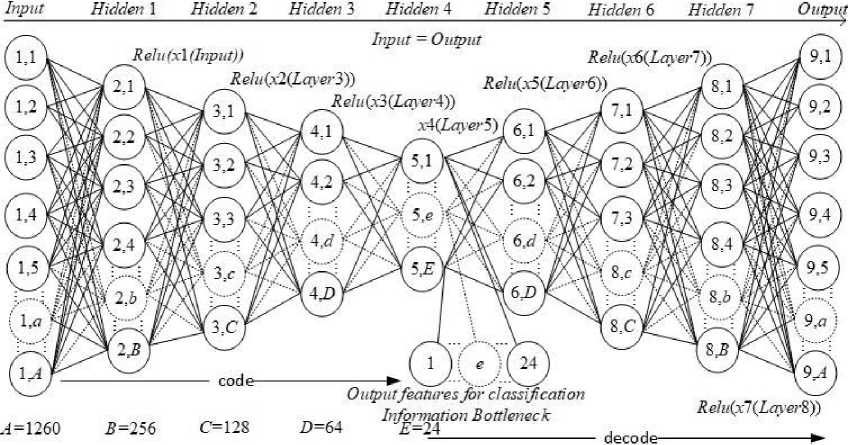
Рис. 1. Граф симметричного многослойного мульти-адаптивного нейрона прямого распространения, обеспечивающий функции кодера и декодера.