Автоматизированная информационная технология разработки и проверки индивидуальных заданий для практики по учебному предмету "Математический анализ"
Автор: Афанасьев Сергей Борисович
Журнал: Образовательные технологии и общество @journal-ifets
Статья в выпуске: 4 т.22, 2019 года.
Бесплатный доступ
В статье предложена информационная технология для разработки и проверки произвольного количества однотипных индивидуальных заданий по математическому анализу. Разработка заданий происходит в автоматическом режиме - достаточно задать количество необходимых заданий и пути к папкам, в которых будут храниться сгенерированные задания и их решения. После получения от студентов результатов выполнения заданий их проверка также происходит с использованием информационной технологии при минимальном участии преподавателя, достаточно задать пути к файлам правильных решений и решений полученных от студентов.
Информационная технология, математический анализ
Короткий адрес: https://sciup.org/140245481
IDR: 140245481
Текст научной статьи Автоматизированная информационная технология разработки и проверки индивидуальных заданий для практики по учебному предмету "Математический анализ"
Вызовы, на которые должна ответить Россия в 21 веке настоятельно требуют улучшения качества образования. Как отмечается в [1] уровень высшего образования такой как среди наших сограждан в возрасте 25-35 лет, имеют всего три страны в мире –Япония, Южная Корея и Канада. Взрывной рост потребности в образовании ожидается и в дальнейшем, по прогнозам высшее образование получает или стремится получить до 80% граждан от 15 до 25 лет. Ясно, что экстенсивный рост возможностей для удовлетворения образовательных потребностей проблемы не решит – необходимо радикальное улучшение качества образования. Один из путей достижения этой цели -внедрение информационных технологий, причём не только на уровень организации учебного процесса, но и внутрь его – на уровень лекций, практических и лабораторных занятий. Актуальная проблема внедрения информационных технологий в учебный процессе затрагивалась в большом количестве работ, посвящённых как общей методологии создания обучающих компьютерных средств [2-6], так и её применению к модернизации курса «Математический анализ» [7-9]. Один из путей внедрения информационных технологий в учебный процесс - тщательный анализ имеющихся «докомпьютерных» методик обучения и разработка информационных технологий для них, там, где это возможно.
Анализ современного состояния проблемы
Все великие педагоги прошлого единодушно отмечали, что одним из важнейших факторов при организации учебного процесса являются систематический контроль результатов самостоятельной работы обучаемых [10].
Этой проблеме посвящены исследования Ю.К. Бабанского [11], В.К. Буряка [12],П.И. Пидкасистого [13] и др. В них были выделены существенные признаки самостоятельной работы обучаемых. Одним из главных является наличие задания, кроме того отсутствие непосредственного участия преподавателя или какого-либо другого «помощника», наличие специально отведённого времени и, наконец обязательный контроль результатов. В настоящее время не так просто организовать работу так, чтобы были выполнены все эти условия. Нет проблем с выделением времени для самостоятельной работы – оно предусмотрено всеми учебными планами. Проблема наличия «помощника», наверное, не решаема в принципе – степень самостоятельности при выполнении работы можно оценить только апостериори в процессе общения со студентом на занятиях или на промежуточной аттестации. Проблемы разработки заданий и их последующей проверки тоже нелегки. Педагог, вынужденный работать с большими группами студентов, физически не в состоянии перманентно анализировать и оценивать индивидуальную работу каждого из обучаемых. По этой причине некоторые студенты позволяют себе выполнять не все задания, иногда на удаётся исправить ошибки, следствием чего является ухудшение качества образования. Интересная методика предложена в [14]. Для группы численностью 25 человек при условии проведения аудиторных занятий 2 раза в неделю студентам выдаются недельные индивидуальные задания. При этом кафедра разрабатывает и выдаёт каждому преподавателю матрицы ответов и банк листов решений. В дальнейшем они используются при самоконтроле правильности выполнения заданий студентами, при взаимном студенческом контроле, а чаще всего при комбинированном, когда преподаватель проверят правильность метода решения, а студент – свои вычисления. Утверждается, что такая методика позволяет проверить индивидуальные задания 25 студентов за 15-20 минут с выставлением оценок в журнал. Можно себе представить тот объём работы, который нужно проделать преподавателям, чтобы разработать такие задания для большого потока, да и 15-20 на каждом занятии тоже немало. В [14] утверждается, что такой подход позволяет отказаться от традиционного итогового семестрового или годового экзамена и проводить итоговую аттестацию по результатам блоков индивидуальных заданий в течение семестра.
Методология и теоретическая часть
Из вышесказанного следует, что глобальный контроль за учебным процессом возможен при условии включении в него информационных технологий, которые позволили бы с одной стороны обеспечить каждого из обучаемых индивидуальным заданием и предоставили бы возможность контролировать выполнение каждого задания каждым из обучаемых с другой стороны. Крайне важно иметь возможность обеспечить каждого студента персональным набором заданий по всем темам изучаемого курса. Задания эти должны быть однотипными с заданиями сокурсников и представлять одинаковую трудность. С другой стороны задания не должны быть одинаковыми.
Достижение этой цели возможно при разработке заданий на основе единого шаблона, в который подставляются параметры, делающие задания отличными друг от друга. Автор давно использует в своей работе такую практику и в настоящее время располагает набором технологий, позволяющим генерировать задания по всем темам практических занятий по предмету «Математический анализ». Для каждой темы разработан шаблон документа текстового процессора Microsoft Word и написан макрос, позволяющий создавать документы на основе этого шаблона. В макросе с использованием генератора случайных чисел создаётся набор параметров, которые затем подставляются в соответствующие позиции шаблона и превращают его в индивидуальное задание. Одновременно с заданием генерируется решение. Решение представляет собой файл табличного процессора Excel, в первом столбце первого листа которого представлены правильные ответы. Задание, аналогичное сгенерированным, разбирается на практическом занятии, где объясняется, как решать каждый из примеров и как результаты решения записать в рабочую книгу табличного процессора.
Домашние задания студенты скачивают из аккаунта Google, который специально создан для этой цели. Логин и пароль на доступ в аккаунт даётся преподавателем. Туда же закачиваются решения. Для автоматической проверки создан файл табличного процессора Excel и разработан макрос, позволяющий эту проверку осуществить. В частности в приведённом ниже примере макрос рассчитан на проверку задания номер один, и предполагает названия файла, в котором содержится решение в виде: R1VNGM. (R1 означает решение первого задания, VN – вариант N, GM группа M. Решения следующих заданий именуются аналогично). Для проверки заданий необходимо скачать набор выполненных заданий из аккаунта и поместить в папку, в которой находятся также полученные ранее верные решения, и файл, в котором будет отражаться результат. Далее следует запустить макрос проверки на исполнение. Результат проверки снова отправляется в аккаунт, где студенты могут его просмотреть, таким образом на следующем занятии возможно обсуждение результатов.
В качестве примера в статье приведены программные продукты позволяющие разрабатывать и проверять задания по теме «Числовые множества».
Шаблон документа для генерации заданий.
-
1. Дано множество {x | x+ = (x+ )}. Чему оно равно
-
2. Дано множество {x |( x+ )= x+ }. Чему оно равно
-
3. Дано множество {x |x= |x|}. Чему оно равно?
-
4. Дано множество {x |x ∈ R , x=>}. Чему оно равно?
-
5. Дано множество {x |x ∈ R, x>}. Чему оно равно?
-
6. Дано множество {x |x ∈ R, <=x<=}. Чему оно равно
-
7. Дано множество {x |x ∈ R,
-
8. Дано множество {x |x ∈ R,
-
9. Дано множество {x |x ∈ R, <=x<}. Чему оно равно?
-
10. Дано множество {x | x*xx +=0}. Чему оно равно
-
11. Дано множество {x |x*x+x+=0}. Чему оно равно
-
12. Найти пересечение двух множеств: {x| x ∈ R, x<},{x| x ∈ R, x>}
-
13. Найти пересечение двух множеств: {x| x ∈ R, x=>},{x| x ∈ R, x<=}
-
14. Найти пересечение двух множеств: {x| x ∈ R, x>}, {x| x ∈ R, x<=}
-
15. Найти пересечение двух множеств: {x| x ∈ R, x=>} ,{x| x ∈ R, x<}
-
16. Найти объединение двух множеств: {x| x e R, x>},{x|x e R, x<}
-
17. Найти объединение двух множеств: {X x e R, x<},{x| x e R, x>}
-
18. Найти объединение двух множеств: {x x e R, x=>}, {x x e R, x<=}
-
19. Найти объединение двух множеств: {x x e R, x>}, {x x e R, x<=}
-
20. Найти разность двух множеств: {x x e R, x=>}, {x x e R, x<}
-
21. Найти разность двух множеств: {x x e R, x>},{x| x e R, x<}
-
22. Найти разность двух множеств: {x x e R, x>}, {x x e R, x<=}
-
23. Найти разность двух множеств: {x x e R, x=>},{x| x e R, x<=}
-
24. A= {x<=x<=}, I={x <=x<=}
-
25. A= {x
-
26. A= {x<=x<}, I={X<=x<=}
-
27. A= {x
-
28. х>=0 и y>a*x и y>b*x*x
-
29. х>=0 и y>a*x и y>=b*x*x
-
30. х>=0 и y>a*x и y<=b*x*x
-
31. х>0 и y>b*x*x и y<=a*x
Найти дополнение множества A к множеству I
На координатной плоскости (x,y) задана прямая y= a*x (a>0) и парабола y=b*x*x (b>0)
Какие из приведённых ниже рисунков соответствует множествам:
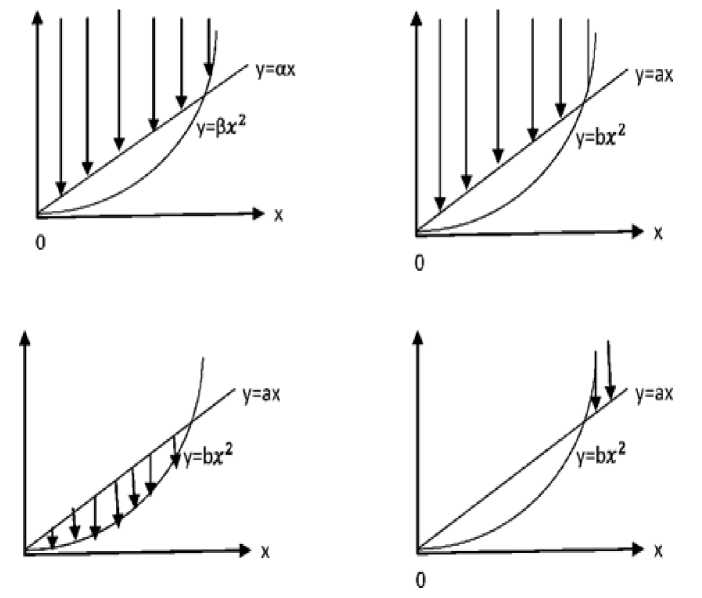
Рис. 1-4. Рисунки к вопросам 28-31
Результаты и их апробация
Как уже говорилось, представленные программы реализуют подготовку заданий и ответов к ним по теме «Числовые множества». Разработка шаблонов, а также макросов генерации и проверки заданий для других тем курса делается вполне аналогично. Ключевой проблемой при разработке заданий является подбор примеров, которые были бы интересными и раскрывали суть изучаемой темы с одной стороны и которые можно было бы тиражировать, меняя в них определённые параметры с другой стороны. Автор располагает программами, которые позволяют создавать индивидуальные задания для практики по всем темам курса. Изложенная методика применялась на протяжении нескольких последних лет в ННГУ при работе со студентами факультета международных отношений (все специальности), экономического факультета (специальности «Прикладная информатика» и «Менеджмент»), студентами института экономики и предпринимательства (специальность «Прикладная информатика»). Результаты работы свидетельствуют о том, что при использовании этой системы студенты гораздо более ответственно подходят к выполнению самостоятельной работы. В конце семестра у преподавателя имеется полная картина работы обучаемых в семестре. Автор согласен с тезисом, высказанном в [14], что в некоторых случаях по итогам работы в семестре студентам можно предложить оценку по промежуточной аттестации без её непосредственного проведения. Это тот случай, когда форма аттестации зачёт, если форма промежуточной аттестации экзамен, то по итогам работы в семестре можно предложить отметку «удовлетворительно». Естественно всё зависит от специальности, по которой обучаются студенты и от степени уверенности в самостоятельности выполнения работы.
В качестве примера рассмотрим вывод оценки по одному из заданий
Одно из сгенерированных заданий по теме «Числовые множества»
Задание 1 вариант 1
-
1. Дано множество {x |3 x+ 4= 3(x+4 )}. Чему оно равно ?
-
2. Дано множество {x |3( 4x+6 )=12 x+18 }. Чему оно равно
-
3. Дано множество {x |x= 4|x|}. Чему оно равно?
-
4. Дано множество {x |x ∈ R 5. Дано множество {x |x ∈ R, 6. Дано множество {x |x ∈ R, 7. Дано множество {x |x ∈ R,
-
8. Дано множество {x |x e R,
-
9. Дано множество {x |x ∈ R, 10. Дано множество {x | x*x 11. Дано множество {x |48x*
, x=>6}. Чему оно равно? x>9}. Чему оно равно? 3<=x<=4}. Чему оно равно? 6 -7x +12=0}. Чему оно равно? x+12x+3=0}. Чему оно равно 12. Найти пересечение двух множеств: {x xeR, x<-3},{x| xeR, x>3} x=>3},{x| xeR, x<=4} x>3}, {X xeR, x<=4} x=>3} ,{X xeR, x<4} 13. Найти пересечение двух множеств: {x xeR, 14. Найти пересечение двух множеств: {x xeR, 15. Найти пересечение двух множеств: {x xeR, 16. Найти объединение двух множеств: {x xeR, x>3},{xxeR, x<4} 17. Найти объединение двух множеств: {x xeR, x<3},{x xeR, x>4} 18. Найти объединение двух множеств: {x xeR, x=>3}, {x xeR, x<=4} 19. Найти объединение двух множеств: {x xeR, x>3}, {x xeR, x<=4} 20. Найти разность двух множеств: {x xeR, x=>3}, {x xeR, x<4} 21. Найти разность двух множеств: {x xeR, x>3},{x xeR, x<4} 22. Найти разность двух множеств: {x xeR, x>3}, {x xeR, x<=4} 23. Найти разность двух множеств: {x xeR, x=>3},{x| xeR, x<=4} 24. A= {x|4<=x<=6}, I={x|3 <=x<=9} 25. A= {X4 26. A= {x4<=x<6}, I={X3<=x<=9} 27. A= {x4 28. х>=0 и y>a*x и y>b*x*x 29. х>=0 и y>a*x и y>=b*x*x 30. х>=0 и y>a*x и y<=b*x*x 31. х>0 и y>b*x*x и y<=a*x Найти дополнение множества A к множеству I На координатной плоскости (x,y) задана прямая y= a*x (a>0) и парабола y=b*x*x (b>0) Какие из приведённых ниже рисунков соответствует множествам: Рис 5. Результат работы макроса генерации. Сгенерированное решение A В C 0 Е F 6 1 Ваше pen Правильное решен Процент верных ответов 100,00% 2 0 0 да 3 R R да 4 [0} {0} да 5 [6,-) [6,-] да 6 (9,-) (9.-) да 7 [3,4] [3,4] да 8 (6.9) (6.9) да 9 (3,4] (3,4] да 10 [6,9) [6,9) да 11 {3,4} {3,4} да 12 0 0 да 13 0 0 да 14 [3,4] [3,4] да 15 (3,4] (3,4] да 16 [3,4} [3,4} да 17 R R Да 18 (—,3),(4, (—,3),(4, Да 19 R R Да 20 R R Да 21 [4,-) [4,-1 Да 22 [4,-) [4,-1 Да 23 (4,-) (4,-) Да 24 (4,-) (4,-) Да 25 [3,4),(6,9] [3,4),(6,9] Да 26 [3,4],(6,9] [3,4],(6,9] Да 27 (3,4),[6,9] [3,4),[6,9] Да 28 [3,4],[6,9] [3,4],[6,9] Да 29 1 1 Да 30 2 2 Да 31 4 4 Да 32 3 3 Да Рис 6. Результат работы макроса проверки –оценка работы по 100 бальной шкале Рис 7. Суммарные результаты Заключение Разумеется, представленная технология далека от совершенства. При её практическом применении иногда возникают вопросы, которые можно разрешить только в личном общении со студентом. Окончательное решение об оценке принимается отнюдь не компьютерной программой, а преподавателем только после обсуждения всех спорных вопросов. Поэтому технология автоматизированная, а не автоматическая. Однако даже в таком виде технология существенно облегчает жизнь преподавателю. После немалых интеллектуальных усилий, связанных с подбором примеров и разработкой шаблона всю остальную рутинную часть работы берёт на себя технология. В перспективе для этих целей возможно применение технологий искусственного интеллекта, когда они станут доступны для рядового пользователя.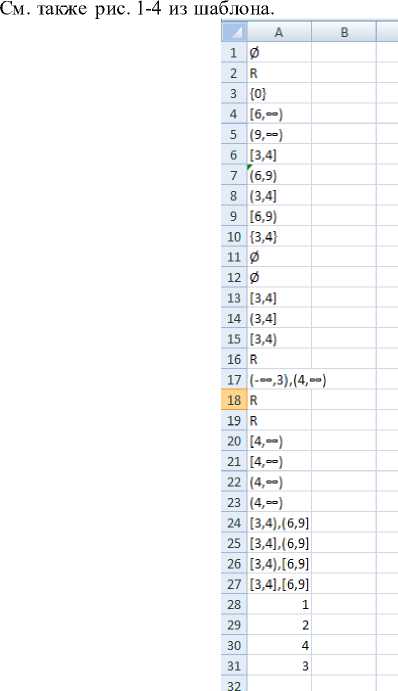
Список литературы Автоматизированная информационная технология разработки и проверки индивидуальных заданий для практики по учебному предмету "Математический анализ"
- Путин В.В. Россия сосредотачивается - вызовы, на которые мы должны ответить // Известия. - 16.01.2011.
- Zakharova I., Kuzenkov O. Experience in implementing the requirements of the educational and professional standards in the field of ICT in Russian education// CEUR Workshop Proceedings Selected Papers of the 11th International Scientific-Practical Conference Modern Information Technologies and IT-Education, SITITO 2016. 2016. С. 17-31.
- Кузенков О.А., Захарова И.В. Взаимосвязь между проектом MetaMath и продолжающейся реформой высшего образования в России //Образовательные технологии и общество. 2017. Т. 20. № 3. С. 279-291.
- Zakharova I.V., Kuzenkov O.A., Soldatenko I.S., Yazenin A.V., Novikova S.V., Medvedeva S.N., Chukhnov A.S. Using SEFI framework for modernization of requirements system for mathematical education in Russia// Engineering Education on Top of the World: Industry-University Cooperation, SEFI 2016 44th Annual Conference of the European Society for Engineering Education. 2016.
- Soldatenko I.S., Kuzenkov O.A., Zakharova I.V., Balandin D.V., Biryukov R.S., Kuzenkova G.V., Novikova S.V. Modernization of math-related courses in engineering education in Russia based on best practices in European and Russian universities //Engineering Education on Top of the World: Industry-University Cooperation, SEFI 2016 44th Annual Conference of the European Society for Engineering Education. 2016. С. 131.
- Трифонов Ю.В.,Афанасьев С.Б., Громницкий В.С. Облачные и суперкомпьютерные технологии в экономической и образовательной деятельности//Экономика и предпринимательство - 2016.- №3, ч.1.- 6 с.
- Кузенков О.А., Кузенкова Г.В., Бирюков Р.С. Разработка фонда оценочных средств с использованием пакета MathBridge//Образовательные технологии и общество. 2016. Т. 19. № 4. С. 465-478.
- Кузенков О.А., Рябова Е.А., Бирюков Р.С., Кузенкова Г.В. Модернизация курса «Математический анализ» в рамках проекта MetaMath //Инновационные методы обучения в высшей школе. Сборник статей по итогам методической конференции ННГУ. ННГУ. 2016. С. 139-142.
- Кузенков О.А., Рябова Е.А., Бирюков Р.С., Кузенкова Г.В. Модернизация программ математических дисциплин ННГУ им. Н.И.Лобачевского в рамках проекта MetaMath //Нижегородское образование. 2016. № 1. С. 4-10.
- Коменский Я.А., Локк Д., Руссо Ж.Ж., Песталоцци И.Г. Педагогическое наследие. сост. В.М. Кларин, А.Н. Джуринский - М.: Педагогика, 1989 - 416 с.
- Бабанский Ю.К. Как оптимизировать процесс обучения: научное издание/М.: Знание, 1978. - 48 с.
- Буряк В.К. Самостоятельная работа учащихся: книга для учителя / В. К. - М.: Просвещение, 1984. - 64 с.
- Пидкасистый П. И. Самостоятельная деятельность учащихся. М.: Педагогика, 1972. 184 с.
- Сборник индивидуальных заданий по высшей математике. В 3-х частях. Под общей редакцией д.ф.м.н.профессора А. П. Рябушко Минск: 1990-1991, ч.1 271 с.,ч 2. 352 с., ч3 288 с.


