Азимутальные моды собственных колебаний цилиндрического пузырька

Задачам, посвященным движению линии контакта трех сред, в настоящее время уделяется пристальное внимание [1, 2]. В классических работах [1–4] изучено растекание жидкости, хорошо или полностью смачивающей материал подложки, для малых значений капиллярного параметра Ca = U*7* /с** ( U ^* – скорость движения контактной линии, П * и с * - коэффициенты динамической вязкости и поверхностного натяжения, соответственно). В последнее время удалось достигнуть значительного прогресса в понимании процессов при более интенсивном движении контактной линии, а также для конечных значений динамического краевого угла [5].

Однако в перечисленных работах рассматривается установившееся движение линии контакта по обработанной подложке. В

Работа выполнена при финансовой поддержке проекта РФФИ № 14-07-96017-р-урал-а.

этом случае жидкость растекается по подложке либо за счет статических внешних воздействий (сила тяжести, центробежная сила и т.д.), либо за счет межчастичного взаимодействия (например, ван-дер-ваальсово притяжение молекул жидкости к подложке). В таких процессах большую роль играет вязкость. Однако при рассмотрении высокочастотного колебательного движения контактной линии ситуация совершенно иная. В этом случае влияние вязкости становится существенным лишь в тонких пограничных слоях вблизи твердой поверхности, а движение контактной линии определяется в основном быстроос-циллирующим полем давления. Следовательно, можно рассматривать невязкое поведение жидкости в ядре, учитывая вязкость лишь внутри динамического пограничного слоя вблизи твердой подложки. Сложные процессы, происходящие в непосредственной близости линии контакта, из рассмотрения исключаются с помощью эффективных граничных условий, накладываемых на динамику видимого краевого угла.

В работе [6], при изучении затухания стоячих волн на поверхности жидкости между двумя вертикальными стенками, было предложено граничное условие, которое предполагает линейную связь между скоростью движения контактной линии и краевым углом (в случае прямого равновесного краевого угла):

^{∂ ζ *} = Λ k ⋅ ∇ ζ ^* , ∂ t

(1.1)

где ζ* – отклонение поверхности от равно- весного положения, Λ∗ – феноменологическая постоянная (постоянная Хокинга), k – вектор нормали к твердой поверхности. При этом условия фиксированной контактной линии и постоянного краевого угла являются частными случаями граничного условия (1.1): ∂ζ* /∂t = 0 и k ⋅∇ζ* =0 соответственно. В [6] было показано, что граничное условие (1.1) приводит к затуханию колебаний, за исключением двух указанных выше предельных значений Λ* . Отметим, что затухание связано, в первую очередь, с взаимодействием движущейся контактной линии с неровностями (шероховатостями) твердой поверхности. В [6] также приведены результаты качественного сравнения с экспериментами. Кроме того, в [6] было продемонстрировано, что шлифовка поверхности увеличивала параметр Λ* в несколько раз. То есть, параметр Λ* характеризует еще и степень обработки поверхности подложки. Таким образом, параметр Λ* зависит от свойств жидкости и поверхности.

Условие (1.1) использовалось при исследовании собственных осесимметричных колебаний жидкой зоны в условиях невесомости в работе [7], собственные колебания полусферического пузырька на твердой подложке и вынужденные колебания под действием поперечных вибраций изучались в [8], собственных и вынужденных колебаний полусферической капли несжимаемой жидкости на подложке [9, 10]. В работах [11–13] использовалось более сложное граничное условие, учитывающее гистерезис краевого угла [14, 15].

Условие (1.1) используется также в работе [16], при изучении собственных колебаний цилиндрической капли несжимаемой жидкости, окруженной другой жидкостью и ограниченной в осевом направлении твердыми плоскостями. В работах [17–19] изучалось поведение сжатой капли, которая в равнове- сии имела форму фигуры вращения, т.е. равновесный краевой угол был отличен от прямого. Учитывалось движение линии контакта с помощью граничного условия, аналогичного (1.1), но допускающего произвольный равновесный краевой угол.

В работах [20–22], при исследовании движения цилиндрической капли жидкости в переменном электрическом поле, использовалось модифицированное условие (1.1): скорость движения контактной линии пропорциональна сумме отклонения краевого угла и скорости быстрых релаксационных процессов, частоты которых пропорциональны удвоенной частоте электрического поля.

Частный случай условия (1.1), свободно скользящая линия контакта, рассматривался в работе [23] при изучении полусферической капли сжимаемой жидкости на подложке и в [24] при исследовании цилиндрической капли несжимаемой жидкости. Другой частный случай, закрепленная линия контакта, например, использовался при исследовании параметрической неустойчивости полуцилиндрической капли слабовязкой жидкости на подложке [25], цилиндрической капли слабовязкой жидкости [26, 27] и при исследовании собственных колебаний жидкой зоны в поле тяжести [28].

В работах [29–31] изучалась осесимметричная мода собственных колебаний и вынужденные колебания цилиндрического газового пузырька в однородном пульсационном поле давления. Трансляционная мода собственных колебаний такого пузырька исследовалась в [32].

В данной работе продолжаются исследования, начатые в работах [29–32] и рассматриваются азимутальные моды собственных колебаний цилиндрического газового пузырька, окруженного несжимаемой жидкостью конечного объема.

2.    Постановка задачи

Рассмотрим колебания газового пузырька, окруженного несжимаемой жидкостью с плотностью ρ* . Здесь и в дальнейшем величины с индексом i относятся к пузырьку, e -окружающей жидкости. Система ограничена двумя параллельными твердыми плоскостями (рис. 1), расстояние между которыми равно h * . В отсутствие внешних сил пузырек имеет форму цилиндра радиусом r* . Краевой угол между боковой поверхностью пузырька и твердыми плоскостями в равновесии равен П2 . На расстоянии R ** от оси симметрии жидкость, окружающая пузырек, ограничена свободной поверхностью.

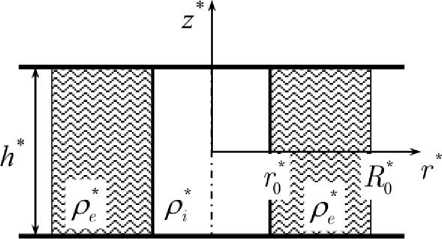
Рис. 1. Геометрия задачи

В силу симметрии задачи будем использовать цилиндрическую систему координат ( r *, а * z z *) , в которой поверхность капли будет описываться уравнением:

* * * * * * r = r0 + Z (z ,а , t ), где Z* (z *, а*, t *) - отклонение поверхности от равновесного положения.

Выберем в качестве единиц измерения времени - рr*3/а* , радиальной координаты - r0*, осевой координаты - h *, отклонения поверхности - амплитуду колебаний A *, скорости - A * ^о*/рr0*3 , давления - A *о*/r7 , где ст* - коэффициент поверхностного натяжения, и ниже запишем все уравнения и граничные условия в безразмерных переменных.

Движение жидкости будем рассматривать как потенциальное. В пренебрежении вязким затуханием давление жидкости будет описываться уравнениями Бернулли, а потенциал скорости – уравнением Лапласа (задача линеаризуется по малой амплитуде внешнего воздействия).

Ре    ^ , Л^е = °’ д t

(2.1)

Здесь введен потенциал скорости жидкости соотношением v = Vp, pe - пульсационное давление жидкости, t = t * Jа*/(р'r7) -безразмерное время. Пульсационное поле p отписывает отклонение давления от равновесного значения.

Газ в пузырьке считаем невесомым. Со- стояние газа описывается политропным про- цессом с показателем политропы n .

В работах [8, 12, 29, 32] было показано, что пульсационное давление газа оказывает влияние только на объемную моду собственных колебаний. Следовательно, при ис- следовании азимутальных мод это давление можно не учитывать, и пузырек ведет себя как капля несжимаемой жидкости.

На поверхности раздела пузырек – жидкость должно выполняться условие баланса нормальных напряжений и кинематическое граничное условие:

r = 1: [p ] = Z + Д + b 2 %, dZ A, да2     dz2   dt    dr

(2.2)

где r = r */r°* , z = z * /h * - безразмерные коор- динаты, квадратными скобками обозначим скачок величины на границе раздела между внешней жидкостью и пузырьком.

На твердых поверхностях необходимо поставить условия непротекания:

z =± 12 : ^- = ° .         (2.3)

d z

Скорость движения контактной линии пропорциональна отклонению контактного угла от равновесного значения [6] :

z =± 1/2 , r = 1 : = m 2 . (2.4) d t d z

Предполагаем, что поверхностное натяжение на внешней поверхности жидкости достаточно мало и им можно пренебречь:

r = R : ^ = ° .               (2-5)

Это модельное условие позволяет не рассматривать движение внешней линии контакта, что технически упрощает решение задачи, оставляя основные эффекты поведения пузырька. Фактически, условие (2.5) означает, что внешняя жидкость окружена невесомым газом с постоянным безразмерным давлением, равным единице.

Краевая задача (2.1)–(2.5) содержит следующие безразмерные параметры:

малую    относительную    амплитуду s = A * P°*, параметр смачивания 2 = Л*/^ре r* /а* , геометрический параметр b = r* hi * , радиус внешней поверхности R = R* /г* , ^ = ® •'рТоРо* - безразмерная частота.

3. Собственные колебания

Рассмотрим азимутальную моду собственных колебаний цилиндрического пузырька с азимутальным числом m >  2 . В дальнейшем под четностью мод будем понимать четность относительно вертикальной координаты. Решение задачи (2.1)–(2.5) будем искать в виде рядов Фурье по собственным функциям уравнения Лапласа (2.1). Для потенциала ^ и отклонения поверхности £ запишем решения следующим образом:

^ e ( r , a,z,t ) = Re ( w ( r,z ) e m e A ) , (3.1)

A m f m 0 я m 0 - A m

y(- 1 ) ¹ A m f m„

^Я m 1 ^- A m

4m² - 1 , ^f 4m² - 1 + 2 ------sh ------

Am ^b    t   2 b  7

Q⁽ ’ >² =

“ m 0

m ( m ² - 1 ) R ^{2 m} - 1

+ ch

= 0 ,

( R ^{2 m} + 1 ) , f_m 0 =

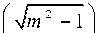
2 b

(3.3)

2 b    , Г 7 m² - 1 "I

,        sh l----------

7 m ² -1 t    2 b    ₇

W ( r , z ) =

= i E ( ( a m1 ^Am’I ( r ) + b e I B m’'1 ( r ) ) C°S ( 2 ~ П2 ) + 1 = 0

+ ( a m'1 A m’1 ( r ) + b m’Bmo,’1 ( r ) ) COS ( ( ² n + 1 ) ^{n z} ) ) ,

^{( e} )

Я)2 = m2 + 4"212b2 -1) -mr при 1 > 1, mn \                      J f (e) Г          ’ mn

Ae ) (R\

F ^{( e} ) = A^(e ) M-R^{1 e} ) fl f   ^{m1 (} __)

' m1 mmn ^(±) mmn ⁽ )    ( e )^ ),

G ⁽ e ) =«⁽ e ) ' f A m ^{1 ( R} ) - e ) 'fH ^u mn   mm,, \ Fg ( e ) ^^ mn ⁽ ) ’

_ 4 ( - 1 ) n b4m ² - 1 f 4m ² - 1 " ^fmn = m ² - 1 + 4 n²1²b ^{2 s} |    2 b J ’

для нечетных мод:

Z ( a , z , t ) = Re ( £ ( z ) e

,im a ’ i A m t )

£ ( z ) = dm ’ ’ ^Ch

4m² - 1 b

t

z

+ d ⁽ ’ ) sh

4m² - 1 b

t

(3.2)

"

^{z +}

у ( - 1 ) n A m g mn n = 0 ° m T ^- A m

+ sh

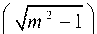
2 b

TO

+ z ( c mn ^cos ( ^{2 n n}z ) + c mon ^cos ( ( ² n + 1 ) ^ z ))’ n = 0

4m² - 1 Л 4m ² - 1

+ 2 ------ch ------

Ab       2b t         7

(3.4)

= 0 ,

где A - частота m-ой азимутальной моды собственных колебаний, ammn , am‘I , bmn , bmn , cm’1 , Cm’l, dm,’), dm,’) — неизвестные амплитуды, л (e) (r\-rm leie} (r\-r~ m ' o )ЛЛ = т fO/7 (НтгЛг! Am 0 (r ) r , Bm 0 (r ) r , Amn (r ) Im ((21 + 1) nbr ) , Bm'1 (r ) = Km ((2n + 1) nbr ) , Am1 (r ) = 1 m (21 Пг )

и A m1 ( Г ) = ^K m ( 2 1 ^Ъг ) при 1 >  ¹ , I m , ^K m - ^мо дифицированные функции Бесселя, i – мнимая единица. Вид решения (3.2) написан исходя из кинематического условия (2.2), а два первых слагаемых (3.2) являются частным решением условия баланса нормальных напряжений (2.2).

Подставляя решения (3.1), (3.2) в задачу (2.1)–(2.5), получаем спектрально-амплитудную задачу, собственными числами которой являются частоты A собственных колебаний. Из решения этой задачи следует, что собственные числа находятся из следующих уравнений:

для четных мод:

_   4 ( - 1 ) n b4rn ² - 1         4m ² - 1 "

= m ² - 1 + ( 2 1 + 1 ) ² n ² b ² c |    2 b   J ’

(o)

Qm12 =(m2 +(21 +1)2 n2b2 -1) G^, mn

A^(o ) (R\

F ^(o) = A^(o ) M - R¹ o ) f 1 'I ^{m1 (} __)

* mn mm n (A) m mn \ Fg ( o )^ j,

Q (^o) ₌D(^O) 'fl \ A ^{m1 ( R} ) _ И o )'/П

G mn B mn ^{( 1)} ft ( o )^^ An ^{( 1 )} ’

Здесь Q ( e ) , Q o ’ - частоты собственных колебаний пузырька со свободно скользящей контактной линией (т.е. при 2 ^» ),

A m^e1 ' ( r ) = A n ( r ) д , A mo ) ( r ) = < 1 ( r )/ S r , A4 ' ( r ) = B ) ( r )> , A o ' ( r ) = A ! . ( r )/ d r ,

f – коэффициенты разложения в ряд Фурье функции ch ( 4m ² - 1 z / b ) по базисным функциям cos ( 2тг ) , g_mn - коэффициенты разложения в ряд Фурье функции sh ( 4m ² - 1 z / b ) по базисным функциям sin ( ( 2 n + 1 ) n z ) .

Уравнения (3.3), (3.4) решались методом секущих.

4.    Результаты

Нетрудно убедиться, что комплексные алгебраические уравнения (3.3), (3.4) имеют комплексные решения, что приводит к затуханию колебаний, которое вызвано диссипацией на линии контакта. Полученные уравнения качественно похожи на аналогичные уравнения для нахождения частот собственных колебаний цилиндрической капли несжимаемой жидкости [16] .

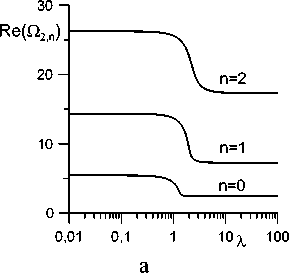
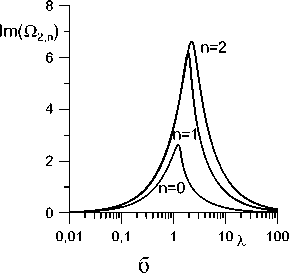
Рис. 2. Зависимость частоты Re (Q₂_J (а) и коэффициента затухания Im (fl₂J (б) от Л для разных n (R = 5 , b = 1 ).

Отметим также, что решения уравнений (3.3), (3.4) будут действительными только в двух предельных случаях: А = 0 (закрепленная линия контакта) и А ^ ж (свободно скользящая контактная линия).

Для удобства будем обозначать частоты четных мод, определяемых уравнением (3.3), Qm2i (m > 2 , k = 0,1,2,...), а частоты нечетных мод, которые являются решением уравнения (3.4), Qm,2к+1 (m > 2, k = 0,1,2,...). Таким образом, все частоты собственных колебаний Qm „ (m > 2, n = 0,1,2,...) с четны ми n будут соответствовать частотам Qm а, а с нечетным n - Q ,  .

m , 2 k + 1

а

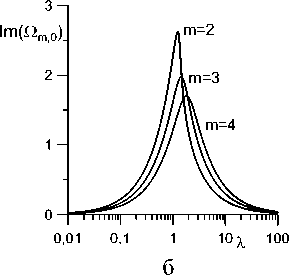
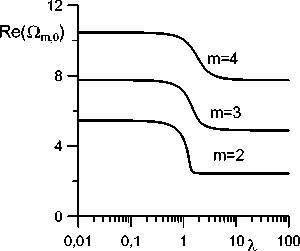
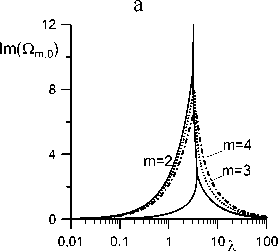
Рис. 3. Зависимость частоты Re ( Q_m0 ) (а) и коэффициента затухания Im (О_{я 0}) (б) от А для разных m (R = 5 , b = 1 ).

Зависимости трех первых частот и коэффициентов затухания О_{2 0} , Q₂₁ , Q₂₂ азимутальной моды m = 2 собственных колебаний от параметра А показаны на рис. 2. На рис. 3 приведены основные частоты и инкременты затухания для трех первых мод m = 2 , 3 , 4 .

Частота монотонно уменьшается с увеличением А (рис. 2,а, 3,а). Наибольшее значение частоты имеет капля с закрепленной линией контакта ( А = 0 ), наименьшее - свободно скользящая капля ( А ^^ ). Максимальное затухание достигается при конечных значениях параметра А . Как уже отмечалось выше, коэффициент затухания Im ( Q ) ^ 0 в предельных случаях А ^ 0 и А ^^ (рис. 2,б, 3,б). Отметим также, что значения инкрементов затухания увеличиваются с ростом волнового числа n (рис. 2,б), т.е. более высокочастотные колебания (рис. 2,а) затухают быстрее.

б

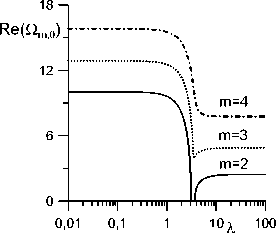
Рис. 4. Зависимость частоты Re ( О_{л 0}) (а) и коэффициента затухания Im (П_{л 0}) (б) от Л для разных m (R = 5 , b = 2 ).

На рис. 4, 5 приведены основные частоты и инкременты затухания трех первых азимутальных мод m = 2 , 3 , 4 для двух значений геометрического параметра b . Сразу отметим, что частота и максимальное значение коэффициента затухания тоже увеличиваются с ростом b (т.е. с увеличением равновесного радиуса или уменьшением высоты пузырька) (см. рис. 3-5).

Действительная часть частоты Qm 0 обращается в нуль на некотором интервале значений Л (рис. 4,а, 5,а) начиная с некоторого критического значения геометрического параметра b . При b = 1 действительная часть основных частот Оя0 не обращается в нуль при любом значении Л (рис. 3,а). Однако при b = 2 уже существует интервал значений Л , на котором Re (п2 0) = 0 (рис. 4,а), а при b = 2 подобные интервалы есть уже для Re (q20) и Re (^30) (рис. 5,а). Появление таких интервалов обусловлено сильным взаимодействием капли с подложкой. Подобное явление было обнаружено для осесимметричных собственных колебаний цилиндрического пузырька [29] и для несжимаемых капель [10, 16]. Кроме этого, в работах [9, 16, 26, 29] было обнаружено, что основная частота трансляционной моды затухает, начиная с некоторого критического значения Л . Это характерное значение Л увеличивается с ростом b .

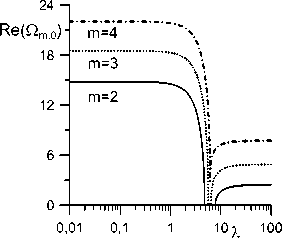
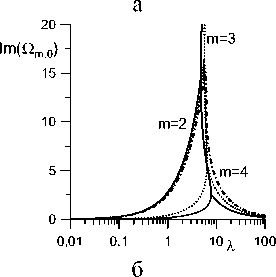
Рис. 5. Зависимость частоты Re (о„0) (а) и коэффициента затухания Im (Рл 0) (б) от Л для разных m (R = 5, b = 3).

Точке обращение в ноль действительной части частоты О_л0 (рис. 4,а, 5,а) соответствует точка ветвления для коэффициентов затухания (рис. 4,б, 5,б). Кроме того, из рис. 4,а и 5,а видно, что значение интервала, где частота обращается в нуль, растет с b .

Кроме колебательного (периодического) режима существует еще и монотонный (апериодический) режим, при котором корни уравнения (3.3) имеют только мнимую часть (рис. 4,б, 5,б). Эти два режима не взаимодействуют до тех пор, пока частота колебательного режима не обращается в ноль.

С увеличением объема внешней жидкости частота (рис. 6,а, 7,а) и декремент затухания (рис. 6,б, 7,б) любой моды уменьшается. Отметим, что значения частот при R = 5 и R = 500 довольно близки, поэтому при больших R можно рассматривать внешнюю жидкость как имеющую бесконечный объем (R ^ж). Подобный результат был получен для осесимметричных поверхностных мод [29–31] и трансляционной моды [32] цилиндрического пузырька. Отметим, что в этом случае значения частот напрямую не приводятся к результатам для капли несжимаемой жидкости [16], где учитывалось движение жидкости внутри капли.

5.    Заключение 0,01    0,1      1      10 ^   100 б Рис. 6. Зависимость частоты Re (П20) (а)

Рассмотрены азимутальные моды собственного колебания цилиндрического газового пузырька, окруженного другой жидкостью со свободной поверхностью и находящегося между двумя твердыми поверхностями. При этом учитывалась динамика контактной линии: скорость движения контактной линии предполагалась пропорциональной отклонению контактного угла от равновесного значения. Коэффициент пропорциональности, так называемый параметр смачивания (постоянная Хокинга), характеризует свойства жидкости и материала подложки. Равновесный краевой угол прямой.

Найдено, что для любой моды собственных колебаний, которая описывает азимутальные колебания пузырька, основная частота колебаний может обращаться в нуль, начиная с некоторого значения геометрического параметра b , на интервале значений параметра Л . Длина этого интервала растет с увеличением b .

и коэффициента затухания Im ( П_]0 ) (б)

от Л для разных R (b = 1 ).

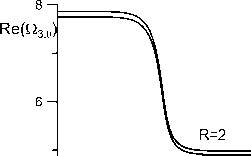
Частоты уменьшаются с увеличением радиуса свободной поверхности внешней жидкости R и увеличиваются с ростом геометрического параметра b . Инкремент затухания также увеличивается с ростом b или волнового числа n . Следует отметить, что значения частот азимутальных мод не зависят от давления газа внутри пузырька.

0,01     0,1      1

I I 11|||||—I I |||||||

10 ^   100

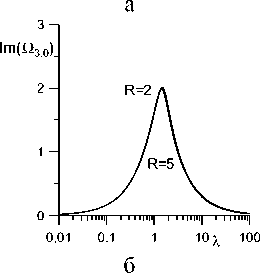
Рис. 7. Зависимость частоты Re ( Q₃₀ ) (а)

и коэффициента затухания Im (Q₃₀) (б)

Показано, что увеличение постоянной Хокинга приводит к уменьшению частоты собственных колебаний. Наименьшую собственную частоту имеет свободно скользящий по твердым поверхностям пузырек.

Автор благодарит Алабужева А.А. за помощь и полезные обсуждения.