Baltic Sea water dynamics model acceleration

The article presents results of computer program modernization. This modernization included rewriting program code to another language and accelerating it. Speed-up was achieved by manual optimizing transformations and nested loops parallelization. Assessment of labour costs for program modernization and the resulting performance increase are presented.

Compiler transformations are not necessarily effective in all cases, so manual program transformations are still valid despite the progress in compiler optimization [1].

This is a. result of group of authors performing modernization of software implementation for BSM-1 (Baltic Sea. Model), which is currently running 24 hours a. day 7 days a. week at the St. Petersburg Flood Prevention Facility Complex [2]. BSM-1 model is based on numerical integration of partial differential equations system based on shallow water theory. The model is the evolution of a. family of BSM (Baltic Sea. Model) models used within CARDINAL software system [3]. This article hereafter describes the modernization process and its results, aforementioned software system is referred to as "model program".

The particularity of the presented article lies in the fact that it describes program optimization process based on optimizing transformations only, without the knowledge of the particular field software it is based on. Using knowledge from this field allows better optimization of software than just working with the source program code [4], but it is more time-consuming.

Current tool kit of software optimizing transformations contains numerous tools to optimize nested loops, which is a reasonable focus for software based on mathematical modelling methods. Nested loops in such programs usually take the largest part of execution time. Their optimization is a priority task, which is solved by parallelizing and other transformations. Currently the software performance is determined not only by code parallelism but optimization of memory accesses [5-8] as well. Optimizations of memory accesses include alignments [9], tiling (transition to block computations) [7,10-13] and unconventional array placements [14-16]. The best performance is demonstrated for the programs that are parallel and optimize memory access simultaneously [6,7,17-20]. The model software, which wasn’t initially optimized in any way, had other time-consuming parts in addition to nested loops. These parts included I/O functions, data structure preparation and elementary mathematical functions.

The model program inherited CARDINAL complex main features. It was written in Object Pascal language using Delphi 6 IDE and included graphical user interface for setting the computational model and the main computational core. Only this core part was subject to optimization.

The software model was subjected to numerous optimizing transformations, many of which cannot be performed automatically by optimizing compilers [6,7]. The task was completed thanks to authors’ experience working on Optimizing Parallelizing system [21].

1.    Underlying Mathematical Model

Consider shallow water ecpiations [3] in curvilinear coordinates in two-dimensional form, that are being solved in the model software:

U t + ( H) x	UV H -	gH 2 -gH ς x -    ρx 2 p о	_ HdP q - ρ 0 ∂x
		- f V - K A U -	C d P q w ( x ) |W 1 — f b UV 1 ρ 0              H 2
V t - ( UH )	-(£) — x     H y	gH 2 H y 2 p о P y	- HdP a - fU - ρ 0 ∂y
		- K A V - C d p a ρ 0	w ( У ) |W | — f b Vzr • H 2

St + Ux + Vy — ws, (cH) t + (Uc) x + (V c) y — KcHA c — AcH - Cs^s — fs, where u, v, w(x,y,z,t) are velocity vector components in Cartesian coordinate system; c(x,y, xz, t) is concentration: T(x,y,z,t) is water temperature: S(x,y,z,t) is salinity: у(x,y,t) is water level: h(x,y) is water• depth: H — h - y: g is free fall acceleration: V is volume of water originating from internal sources in volume units per second; cs is sources concentration; A is non-conservative factor; kc, Kc are diffusion coefficients in vertical and horizontal directions; wо is vertical speed sedimentation of suspended solids; K и k are turbulent viscosity coefficients in vertical and horizontal directions; PA is atmospheric pressure: W is wind speed: p is water density: f — 2ш sin ф is Coriolis parameter: U and V are total flows (unit discharge); us is water volume coming from internal sources per unit area per second; fb is bottom friction coefficient.

2.    Software Optimization Methods

The following is done to the model program:

• 1.    Program profiling for typical input data sets.

• 2.    Finding program hotspots based on profiling results.

• 3.    Experimental attempts at hotspot optimization. Goal of these experiments was to quickly identify the most efficient optimization method for particular pieces of code. Experiments are carried out for functions within source program or with the same functions but separated into individual programs for simplicity.

• 4.    Optimization of program hotspots with chosen methods. Resulting speed-up measurement.

• 5.    Testing the optimized program for correctness. Testing is performed by comparing modified functions with their original counterparts on the same input datasets.

• 6.    Optimized program profiling to find new hotspots.

Operations mentioned above constitute an iterative development process which is based on the source program. The process stops when the required criteria are met.

The program optimization consists of a set of operations that reduce program execution time in typical use cases (on typical input data). Those operations may include:

• 1.    Optimizing transformations including loop parallelization and other loop nest transformations. It makes sense to separate program transformations into groups:

• (a)    Paralellizing loop transformations.

• (b)    Loop optimizing transformations such as fission, unrolling, invariant extraction, etc.

• (c)    Operator-level parallelization.

• (d)    I/O optimization, including splitting I/O operations into separate thread.

• (e)    Other optimizing transformations, such as inlining, common subexpression elimination ...

• 2.    Rewriting parts of it or entire program into another programming language.

• 3.    Replacing program parts with third-party library function calls.

• 4.    Testing resulting program correctness and performance.

3.    Labour Costs Distribution

Rewriting entire program to another language is perhaps the most expensive way to increase performance. This, however, may improve other characteristics, such as ease of support and reuse, apart from performance. Rewriting is justified if the source program language lacks comprehensive optimizing compilers, high-performance libraries or its use is not justified for some other reasons. In case of model software it was Object Pascal used in Embarcadero Delphi 6.0 IDE. Main computational part was ported to CT language for Microsoft .NET 4.0 platform, which was done for ease of maintenance as well as performance boost.

It’s important to identify where most of the labour and time will be spent during sizeable program optimization. Working on model program showed the following main cost items:

• 1.    Porting the program to another programming language.

• 2.    Adding unit tests for all ported modules.

• 3.    Profiling and finding suitable optimization methods.

• 4.    I/O optimization.

• 5.    Computational functions optimization including parallelization.

• 6.    Functional testing and debugging.

• 7.    Performance testing and performance analysis on the target computing system.

4.    Porting into C#. Results

In total, the cost of model program modernization amounted to about 60 man-months.

The labour costs distribution for the items listed above is shown on Fig. 1.

Fig. 1. Labour costs in model program modernization

Porting the model program into more modern language provided considerable performance increase. Table 1 shows comparison of execution times for main computational functions (that include nested loops), which took most of the program execution time. Performance boost achieved through porting to C# is 45%. All of this boost is due to better optimizing compiler for .NET platform. Compiler was able to perform inlining of small functions called from inside nested loops, as well as other optimizations. Apart from that, .NET standard library includes faster mathematical functions.

Table 1

Speed-up clue to rewriting main computing functions, sec.

	TimeStep	GetPStar	GetQNew	QStar	PNew	DryCells
Source program	644	167	180	85	78	111
Optimized program	501	144	149	66	58	61
Speed-up	1,28	1,16	1,2	1,28	1,34	1,81

5.    Program Modules Dependencies

Porting tens of thousands lines of code to a different language is cpiite an ambitious task taking into account necessary testing. The model program was subdivided into modules. Directed graph of modules dependencies was developed in order to determine module porting order. Unit dependencies appear because of access to global variables, functions or types. If unit A uses data types or functions declared in unit B, the graph has an edge leading from A to B. Edges determine the order of porting modules: from two modules the dependent one is ported later. This order simplifies porting and testing. Modules dependencies graph is similar to function call graph [22]. This graph for the model program is shown on Fig. 2. Typically the module hierarchy contains service units with simple auxiliary I/O functions and user input processing at the very bottom. It’s reasonable to start porting the program from the lowest hierarchy level, sequentially climbing up with the completion of each level.

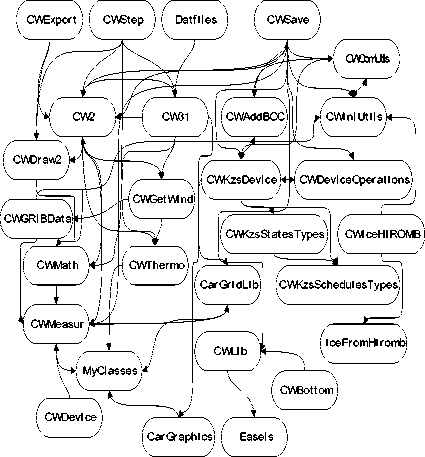
Fig. 2. Some source code modules dependencies within model software computational kernel

Porting order may be formally obtained as follows:

• 1.    Construct the module dependency graph.

• 2.    Construct a strongly connected components factor-graph for the module dependency graph.

• 3.    The resulting factor-graph is acyclic, therefore there is a tiered form for it. Find this form. It has no edges between nodes within single tier and any edge goes downwards.

• 4.    Modules porting order is given by tiers from bottom to top.

6.    Program Transformations Used

The model program transformations used are listed in Table 2.

Table 2

Program transformations used

Transformation name	Program parts being transformed	Properties
Inlining	Nested loops inside hotspots, I/O, data preparation	Done automatically by the compiler for simple cases. Done manually for some hotspots
Loop invariant extraction	Nested loops inside hotspots	Allows to parallelize some loops due to data dependencies elimination
Loop interchange	Nested loops inside hotspots	Changing the order of matrix traversal which often benefits performance
Loop unrolling	Nested loops inside hotspots	Decrease the added cost of loops
Instruction extraction into a new function	Data preparation functions	Improves code readability and decreases its volume
Common sub expressions elimination	Nested loops inside hotspots	Common sub expressions could be loop invariants that are possible to extract
Loop parallelization	Nested loops inside hotspots	Done for loops without data dependences that prevent parallel execution
Asynchronous function calls	I/O	Allows to extract I/O into separate threads
Dead code removal	Data preparation functions
Replacing global variables by local ones	Nested loops inside hotspots	Eliminates dependencies allowing parallelization
Extension of scalars (replacing a scalar variable with an array)	Nested loops inside hotspots	Eliminates dependencies allowing parallelization

Some transformations listed should be performed in specific order to obtain the highest speed-up. For example:

• 1.    Common sub expressions elimination.

• 2.    Loop invariants extraction.

• 3.    Loop parallelization.

7.    Parallelization

Finding an optimal manual transformation order is easy in some basic cases, while modern optimizing compilers lack such a mechanism. Optimizing transformations interrelation resulting in final speed-up is a complex and less studied process.

Program hotspots usually contain nested loops that perform calculations over data arrays. Parallelizing nested loops may provide the highest benefit compared to other program optimizations, but not all the loops could be parallelized due to data dependencies between iterations.

While working on the model software it was impossible to apply automatic tools. Manual data dependency analysis did not show any dependencies that could prevent parallelization. The most time consuming loops were transformed into parallel form with application of TPL (.NET Task Parallel Library). TPL is the main parallel execution tool for Microsoft .NET 4.0 platform. TPL use is comparable with OpenMP in many cases, keeping the code readability and maintainability.

Matrix elements are being read and written in parallelized two-dimensional loops. Matrix traversal is performed through even rows or columns in each iteration. Loop parallelization is performed as shown in Figure 3 for rows. Arrows demonstrate the order of matrix elements being written. Points without arrows going to them are not overwritten.

Fig. 3. Matrix element traversal order and its distribution into threads

Writing each row or column is separated into a parallel thread. This means outer loop parallelization for a two-dimensional nested loop. Table 3 demonstrates one loop nest before and after parallelization. Main computational functions speed-up as the result of parallelization is shown in Table 4. Substantial performance boost was obtained. But the performance increases disproportionately to the thread number increase due to low memory access speed compared to the speed of calculations inside the loops.

Table 3

Loop parallelization example

Source loop	Parallel loop
int i ; i = g . Lbe + 1; while (i <= g. Len — 1) { int j = g . Nbe ; • •   • while (j <= g . Nen) { • •   •	int i ; i = g . Lbe + 1; int st art I = (g.Lbe + 1) / 2; int finishl = (g.Len — 1) /2+1; P arallel . For ( startl , finishl , index => { int i = index * 2; int j = g.Nbe ; • •   • while (j <= g . Nen) { •   • •

Table 4

Function name	Sequentially	In parallel on 4 cores, 8 threads	Speed-up
GetPStar	75,8	22	3,4
GetQNew	81,8	25	3,3
QStar	32,9	8,4	3,9
PNew	23	6,3	3,6
WaterLevelStar	4,8	1,7	2,8
WaterLevelNew	4,8	1,6	3,0
DryCells	33	11,2	2,9

Main functions speed-up clue to parallelization on 4-core processor, sec.

Conclusion

Main results of this work are:

• 1.    New implementation of BSM-1 was created. It performs 3-7 times faster in typical use cases.

• 2.    Structured approach to old software modernization is described.

• 3.    Set of practical software optimization methods is listed.

The performance boost obtained is shown on Fig. 4. Execution time shown is for 7 different data sets while using different numbers of threads. Performance was measured on 6-core Intel Core i7-3930K processor with 8GB DDR3-1600 memory in single channel mode. This computer system provided best results for optimized program. One can see that performance boost was largely not achieved with parallelization: optimized program operates sequentially 4 or more times faster than the original. While testing the optimized program on several computing systems discovered performance differences obviously were dependent on the following system features:

• 1.    Memory Bandwidth.

• 2.    The number of CPU cores.

• 3.    Memory hierarchy, including different levels of cache.

• 4.    CPU performance.

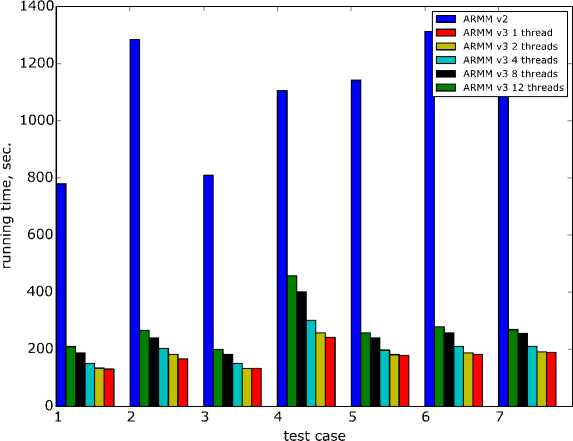
Fig. 4. BSM-1 speed-up for the set of 7 typical tasks

One needs to take these differences into account when optimizing software for high-performance computing system (server, cluster or supercomputer).