Бифуркации сшитого фокуса кусочно-гладкой динамической системы с центральной симметрией

Изучению локальных бифуркаций кусочно-гладких динамических систем на плоскости посвящено значительное число научных работ. Наибольший интерес представляют бифуркации рождения периодических траекторий из особых точек. Различные варианты бифуркаций сшитого фокуса в семействах кусочно-гладких динамических систем, зависящих от одного или двух параметров, рассматривались в [1–6]. В приложениях часто используют дифференциальные уравнения, инвариантные относительно центральной симметрии. Поэтому естественной является задача описания бифуркаций сшитого фокуса в типичных семействах кусочногладких систем с такой симметрией. В настоящей работе она будет решена для одно- и двухпараметрических семейств. Условия, выделяющие такие семейства, даются в явном виде через коэффициенты тейлоровских разложений компонент векторных полей семейств.

1 Условия и результаты

Пусть X ⁺ - C -векторное поле ( r >  5), заданное в верхней полуплоскости R + : = {( x , у ) g R ² : у >  0}. Преобразование центральной симметрии S :( x , у ) a ( - x , - у ) переводит векторное поле X ⁺ в векторное поле X ^-, заданное в нижней полуплоскости R - : = {( x , у ) g R ²’: у <  0} : V ( x , у ) g R - X ^- ( x , у ) -- X ⁺ ( - x , - у ). Векторные поля X ⁺ и X ^- определяют кусочногладкое векторное поле X - ( X ⁺, X ^-) на R ² [1; 3; 6]. Обозначим X S множество таких векторных полей .

Будем рассматривать семейство векторных полей X _ц - ( X Ц , X _ц ) gX^r_s , зависящих от параметра ц - ( Ц 1 ,..., ц _п ), меняющегося в некоторой окрестности нуля в пространстве      R ⁿ     ( n >  1). Пусть

X Ц ( x , у ) = ( P ( x , у , Ц ), Q ( x , у , ц ) ) , где P и Q - C^r -функции,

P(x,у, Ц) = ^ pmn (Ц)Х^” + О((X2 + у2)2),

0 < m + n < 4

Q ^{( x} , у , Ц ) = ^ q mn ⁽ Ц ) х ” у " ⁺ О ^{(( x 2 +} у ^{2)2 )} .

0 < m + n <  4

Обозначим      P mn : = р mn ⁽⁰⁾ ,      Q mn : = q mn ⁽⁰⁾ ,      P mn , , : = 5 p mn ^(0)/ 0Ц ,

4mn,k :=dqmn(0)/дц (k - 1,...,n). Будем предполагать, что p00 < 0 , q00 — 0 , q10 > 0 .

Тогда уравнение Q ( x ,0, ц ) = 0 имеет решение x = ^ ( ц ), определенное в некоторой окрестности нуля в пространстве параметров , при этом

^(0) = 0, ^Цk (ц) = -q00,k Iq10 (k = 1,...,n),(2)

sgn Q (x ,0, ц) = sgn( x - ^( ц));(3)

функция R ( x , у , ц ): = Q ( x , у , ц )/ P ( x , у , ц ) определена в некоторой окрестности нуля в пространстве переменных ( x , у , ц ). Нетрудно убедиться, что

R ( x , у ,0) = ^ r mn x^myⁿ + o (( x ² + у ²)²),

1 < m + n < 4

где

_ ^P 00 ^q 02   ^P 10 ^q 01

^r 02          /    x2

^{( P} 00 )

„ _ ^q 10 „      q 01 „    ^P 00 ^q 20 ^p 10 ^q 10

^r 10  ---- , ^r 01 =----, ^r 20 =----;—72----

P 00         P 00             ^{( p} 00 )

p 00 q 11

r, =-------

—

^p 10 q 01

⁽ P 00 ^{) 2}

—

p 01 ^q 10

,

_ ^{( p} 00 ) q 30   ^p 10 ^{( P} 00 q 20    ^p 10 q n)   ^P 00 ^P 20 q 10

^r30                                /     x3                             ,

^{( p} 00 )

_ ⁽ p 00 ) q 21    ^p 10 ⁽ p 00 ^q 11

r 21

—

p 10 q 01

—

⁽ P 00 ^{) 3}

p 01 q 10 )  p 00 p 20 q 01

,

_у - q 40

P 00

—

P io

( p 00 ) q 30    p 10 ⁽ p 00 q 20    p 10 q io )   p 00 p 20 q 10

( P 00 )⁴

—

—

p 20 ⁽ p 00 q 20   ^p 10 q 10 ⁾    p 30 ^q 10

⁽ P 00 ^{) 3}

—

⁽ P 00 ^{) 2}

Из [1, с. 175-177] следует, что найдется такое число d >  0 , что при всех ц , достаточно близких к нулю, £ ( ц ) е ( — d , d ), равенство (3) выпол-

няется для всех x е [ — d , d ], а положительная полутраектория поля X ц , начинающаяся в точке с координатами ( x ,0), x е [ £ ( ц ), d ], кончается в

точке с координатами (ст + (x, ц), 0), ст + (x, ц) = 2^ (ц) — x + A (ц)(x — ^( ц ))2 — A 2(ц)( x — ^( ц ))3 + + K(ц)(x — ^(ц))4 + s(x — ^(ц), ц),

где

s ( • , • ) - C ^r -функция в окрестности точки (0,0), s ( и , ц ) = o ( и ⁴),

A ( ц ) = 3

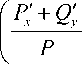
О" I

— Q xx- I ( ^ ( ц ),0, ц ),

K (0) = 11( A ’(0) + r ij A ⁰ ) +

. ² Г ^r 01 ^{( r} 20 )      ^{2( r} 20 )    ^         ^{2 r} 01 ^r 30

⁺ 15 1 , r . )     , r . )     ² r ⁰ r ⁰ 2^— —

^{5 Г} 20 ^Г 30 , <   \ 2 ⁺ ' 21

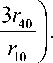
Из (6) и (2) получаем

A ⁽⁰⁾ = I

A (0) = ^{2(( P i:} '

^ц к ^{v 7}    3

^p 10 ⁺ q 01

v    ^P 00

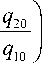
⁺ q 01, k ) q _to ^{— (2} p 20 ⁺ qg) q 00, k ) p 00 ^{— (} P 10 ⁺ q 01X p 00, k q_w ^q 10 ^{( P} 00 )

^p 10 q 00, k )

^{2 (} q 20, k q 10    ³ q 30 q 00, k ) q 10    q 20 ⁽ q 10, k q 10    ² q 20 q 00, k

•

3                               ( q 10 )³

k = 1,

n .

Теорема 1. Пусть n = 1 , выполняются условия (1), А (0) >  0 , ^ ‘ (0) >  0 . Тогда существует окрестность U точки O и число 5 >  0 такие, что для векторных полей X _р , р | <  5 , в U справедливы утверждения:

При р = 0 поле X _р имеет единственную особую точку O, все остальные траектории ш -предельны к O и выходят из U при убывании времени (рис. 1б).

При -5 <  р <  0 поле X _р имеет три грубые особые точки O ±± = ( ± ^ ( р ),0) и O, а также грубую устойчивую периодическую траекторию Г ( р ) . Остальные траектории ш -предельны к Г ( р ) , за исключением двух, кончающихся при возрастании времени в точках O ± . Траектории в области G, ограниченной Г ( р ) , за исключением двух, кончающихся при убывании времени в точках O ± , a -предельны к O; траектории, начинающиеся в U \ G, выходят из U при убывании времени (рис. 1а).

При 0 <  р <  5 поле X _р имеет особые точки O ± = ( ± ^ ( р ),0) и O . Остальные траектории ш -предельны к O, кроме двух, кончающихся при возрастании времени в точках O ± , и выходят при убывании времени из U, за исключением двух, кончающихся в точках O ± (рис. 1в).

Замечание 1 . К случаю, рассмотренному в теореме 1, сводятся случай А ₀ <  0 - переходом к семейству - X _р (на рис. 1 надо обратить стрелки на траекториях), случай ^ ‘ (0) <  0 - заменой параметра р a - р .

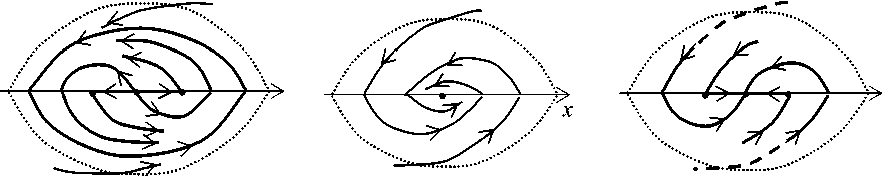
о) /z < 0                        б)д = 0                         в) /z > 0

Рис. 1. К теореме 1. Перестройки фазовых портретов

Теорема 2 . Пусть n = 2 , выполняются условия (1), А (0) = 0 , K (0) >  0 , T

С /⁰) А ₂( ^{0) -} ^С ⁰ ) ^А р , (0) * 0 . Пусть г = ( s , , s ₂) ^а р = ⁽ р , , р , ) - отображение, обратное отображению р a ( s 1 = - А ( р ), s ₂ = ^ ( р )) в некоторой окрестности точки р = 0 . Тогда существуют окрестность U точки O , число 5 >  0 и разбиение области ( -5 , 5 )² изменения параметров s = ( s 1 , s ₂) на множества В ₀ = {(0,0)} , B 1 = (0, 5 ) х {0} , B ₂ = { s : s ₂ = b ( s 1 )} , где b :(0, 5 ) а (0, 5 ) , b е C ¹ , b ( + 0) = b ‘ ( + 0) = 0 ,

В ₃ = ( -5 , 0) x {0} , и множества E _k, k = 1,2,3 , являющиеся связными компонентами ( - 5 , 5 )² \ U k = ₀ B _k, граница которых содержит B _k и B _{k + 1} (здесь B ₄: =B j ) (рис. 2), такие, что для векторных полей X T _{( £} ) , £ е ( -5 , 5 )² справедливы следующие утверждения:

При £ еВ ₀ и £ еВ ₃ поле X T _{( £} ) имеет в U устойчивый сшитый фокус O . Все остальные траектории ω -предельны к O и выходят из U при убывании времени (рис 2).

При £ еВ , поле X T _{( £} ) имеет в U неустойчивый сшитый фокус O и устойчивую грубую периодическую траекторию. Остальные траектории ω -предельны к периодической траектории и либо a -предельны к O, либо выходят из U при убывании времени (рис 2).

При £ еЕ , поле X T _{( £} ) имеет в U три грубые особые точки O £± = ( ± £ ₂,0) и устойчивый узел O, и две грубые периодические траектории, устойчивую и неустойчивую. Поведение остальных траекторий изображено на рис 2.

При £ еВ ₂ поле X T _(Е) имеет в U три грубые особые точки -О ± = ( ± £ ₂,0) , устойчивый узел O и единственную периодическую траекторию – двойной цикл. Поведение остальных траекторий изображено на рис. 2.

При £ еЕ ₂ поле X T _(Е) имеет в U три грубые особые точки -O _£ = ( ±£ ₂,0) и устойчивый узел O. Поведение остальных траекторий изображено на рис. 2.

При £ еВ ₃ поле X T _(Е) имеет в U устойчивый сшитый фокус O. Все остальные траектории ω -предельны к O и выходят из U при убывании времени (рис. 2).

При £ еЕ ₃ поле X T _{( £} ) имеет в U три грубые особые точки -O _£ = ( ±£ ₂,0) , неустойчивый узел O и грубую устойчивую периодическую траекторию. Поведение остальных траекторий изображено на рис 2.

Замечание 2 . Случай K (0) <  0 сводится к рассмотренному случаю переходом к семейству - X _ц (на рис. 2 следует изменить направление на траекториях на противоположное).

Замечание 3 . Из теорем 1, 2 и работ [1; 4; 5] видно, что бифуркационные диаграммы типичных одно- и двухпараметрических деформаций векторного поля с сшитым фокусом в пространстве плоских C^r -векторных полей с центральной симметрией такие же, что и в пространстве всех плоских C r -векторных полей.

Доказательство теоремы 2 приведено в п. 2. Более простое доказательство теоремы 1 мы опустим.

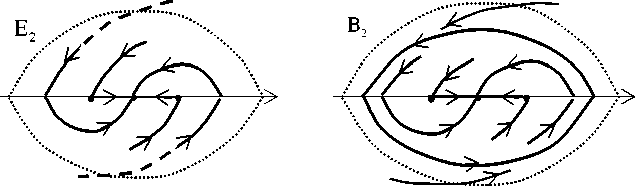
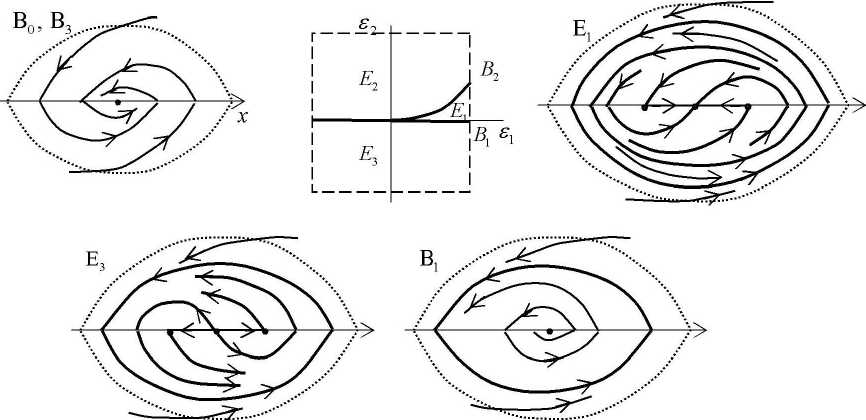
Рис. 2. К теореме 2. Бифуркационная диаграмма

2 Доказательство теоремы 2

Пусть с т ( x , £ ) : = т + ( x , T( £ )). Из (4) и определения T ( £ ) имеем т ( X , £ ) = 2 £ ₂ - x - £ 1 ( x - £ ₂)² - £ 1 ²( X - £ 2 ) 3 +

+ K(T(£))(X - £2)4 + 5(X - £2, T(£)), где 5 удовлетворяет условиям (5).

Выберем такое 51 е (0, d), что т(x,£) определена при £ е[-51,51 ]2, x е [£2,d]. Тогда траектория поля Хт^£), начинающаяся в точке x е[-d,-£2), кончается в точке (-т(-x,£),0). Поэтому функция f£ (x):=-т(-т(x, £),£) является функцией последования по траекториям поля Хт(£). Она определена при тех значениях x е (£2, d], для которых т(x,£) е[-d,-£2). Введем также функцию А(x,£):= т(x,£) + x . Ее роль объясняется в следующей очевидной лемме.

Лемма. 1) В точках x из области определения функции fε sgn(fE (x) - x) = - sgn A( x, £);

• 2)    f _E ( x * ) = x * , ( f _£ ) ‘ ( x ^ ) <  1 (соотв. ( f _£ ) ‘ ( x ^ ) >  1 ) тогда и только тогда, когда А ( x * , £ ) = 0 , A'_x ( x * , £ ) >  0 (соотв. A'_x ( x * , £ ) <  0 );

• 3)    f _E ( x * ) = x * , ( f _£ ) ‘ ( x * ) = 1, ( f _£ ) ‘‘ ( x * ) ^ 0 тогда и только тогда, когда А ( x * , £ ) = A x ( x * , £ ) = 0, A xx ( x * , £ ) ^ 0.

Из (7) и (5) получаем

а ; ( X , £ ) = - £ ( X - £ 2 )[2 + 3 £ 22 ( X - £ ₂)] + 4 K(T( £ ))( X - £ ₂)³ + l ( X , £ )( X - £ ₂)⁴ . (8) где l - ограниченная функция. Из (7), (8) и условия K (0) >  0 следует, что найдется сколь угодно малое число X >  0 такое, что А ( X , 0) >  0, A X ( X ,0) >  0. При достаточно малом 5 = 5 (X ) е (0, 5 1 ), 5 <  X , будем иметь

A(X, £) > 0, AX (X, £) > 0 при всех £ е (-5,5)2,(9)

Кроме того, из (7), (5) и условия K (0) >  0 получаем, что X и соответственно 5 можно выбрать столь малыми, что

A £ (x, £) > 1/2 при всех £ е (-5,5 )2, x е (£ 2, X ] .(10)

Поскольку f,(x) = x- 2K(0)x4 + o(x4), то x и 5 можно считать такими, что f,(x) < x при всех x е (0,x].(11)

Ввиду (11) мы можем аналогично [8, п. 3.14] построить простую замкнутую кривую y , состоящую из гладких дуг у ₊ ^с R + и у - ^с R - с общими концами в точках ( f , ( x ),0) и ( ^( т ( x ,0) + < т ( f _}( X ),0)),0 ) , таких, что векторные поля, соответственно X 0 + и X 0 им трансверсальны и направлены в их точках внутрь области U , ограниченной у • Вследствие (11) все траектории поля X ₀, начинающиеся в U , о -предельны к точке О и выходят из U при убывании времени. Считая 5 выбранным достаточно малым, получим, что при £ е ( - 5 , 5 )² траектории векторных полей X T ( _£ ) в точках у входят в U , а векторные поля X ± не имеют в U особых точек.

Найдем особые точки векторных полей X _£ , £ е ( - 5 , 5 )². Поскольку (3) справедливо при всех x е [ - d , d ], £ е ( - 5 , 5 )², точки О £ : = ( ± £ ₂,0) являются особыми; при £ ₂ >  0 ( £ ₂ <  0) отрезок [ О £ О £ ] оси x между ними -устойчивая (неустойчивая) линейная особенность в терминологии книги [1] . Если точка ( x ,0) е [ О - О + ], то, считая 5 достаточно малым, получаем, что

-1/20,(12)

0< Q(x,0,£) + Q(-x,0,£) < 1/2 при £2 <0,(13)

в выпуклой оболочке векторов X - _£ ) ( x ,0) и X + _{( £} ) ( x ,0) существует единственный вектор X _£ ^o ( x , 0) = ( P₀ ( x , £ ),0),

P (X, 0, £) Q (-X, 0, £) - P (-X, 0, £) Q ( X, 0, £) -Ln. ( X , £ ),

⁰                   Q ( X ,0, £ ) + Q ( - X ,0, £ )

касательный к [ O _E O £ ] . Дуги траекторий поля X £ на [ O _E O £ ] являются и дугами траекторий поля X T _(Е). Так как

( Po X (0, 8 ) = [ - P (0,0, е ) Q (0,0, 8 ) + P J(0,0, s ) Q (0,0, s )] /2 Q (0,0, s ), то с учетом (1), (12) и (13) можно считать, что ( P₀)'_x (0, 8 ) <  P (0) Q X (0) <  0 при s ₂ >  0 и ( P₀) ' _x (0, s ) >- P (0) Q X (0) >  0 при г ₂ <  0. Поскольку P ₀(0, г ) = 0, то 5 можно предполагать столь малым, что O - единственная особая точка поля X_E ⁰, устойчивая (неустойчивая) при s ₂ >  0 ( s ₂ <  0). Для поля X_T (_Е) точка O - грубая особая точка - устойчивый (неустойчивый) узел.

При 8 ₂ = 0 A ( x , 8 ) = - е . x ² + o ( x ²). Если x >  0 достаточно мало, то sgn А ( x , 8 ) = - sgn e . . Вследствие пункта 1) леммы при е . <  0 ( е . >  0) f _E ( x ) <  x ( f _£ ( x ) >  x ), и потому O - устойчивый (неустойчивый) сшитый фокус.

Из выбора окрестности U и поведения траекторий поля X _E ⁰ следует, что любая траектория поля X_{T ( E} ) , е g ( - 5 , 5 )², отличная от особой точки, пересекает отрезок J _E : = [| 8 ₂1, x ] х {0}.

Пусть £ g (0, 5 ) х ( - 5 , 5 ). Тогда A x ( е ₂, е ) = 0, A xx ( е ₂, е ) = - 2 е_х <  0. Отсюда и из (9) следует, что A(, е ) имеет точку минимума m ( е ) g ( e ₂, x ). Покажем, что x и 5 можно считать выбранными так, m ( е ) - единственная критическая точка на ( е ₂, x ) и она невырожденная.

Пусть и - критическая точка функции A(, е) на (е2, x), то есть Ax (и, £) = 0. Считая x и 5 достаточно малыми, отсюда и из (8) имеем е. /(3K(0)) < (и - 82)2 < 2е. /(3K(0)).                     (14)

Из равенства

A xx ( и , £ ) = - 2 e , - 6 e ²( и - 8 ₂) + 12 K(T( £ ))( и - 8 ₂)² + 5 " ( и - 8 2 , T ( £ )) при достаточно малых x и δ получим оценку

A xx ( и , E ) >- 2 е . - 6 е .² ( и - е ₂) + 11 K (0)( и - е ₂)².                (15)

Из (14) и (15) имеем, считая 6 5 ² x <  5/3,

A xx ( и , £ ) >- 2 е ₁ - 6 5 ² x £ . + 11 е ₁/3 = £ 1 (5/3 - 6 5 ² x ) >  0.

Таким образом, любая критическая точка функции A(,е) на (е2,x) является невырожденным минимумом. Следовательно, m(е) - единственная критическая точка, m(•) g C1 и sgn Ax (x, e ) = sgn( x - m (e )) для e g (0,5) х (-5,5), x g (e 2, x).    (16)

Пусть h(e):=A(m(e), e). Из равенства A(e2,e) = e2, (16) и (9) следует, что h(£1,0) < 0 при всех £1 е (0,5).

При £ ₂ = £ 1 е (0, 5 ), x е ( £ ₂, x )

А ( x , £ ) = £ 2 (2 - ( x - £ ₂)² - £ ₂( x - £ ₂)³) + K ( T ( £ ))( X - £ ₂)⁴ + $ ( X - £ ₂, T ( £ )) .

Следовательно, x и 5 можно считать выбранными так, что А(x, £) > 0 при всех x е (£2, x). Поэтому и h(£) > 0 при всех £2 = £1 е (0,5).

Из (10) и (16) получаем, что h£ (£) > 0 при всех £е (0,5) х (-5,5). Отсюда из (17) и (18) следует, что существует такая C1 -функция b :(0,5) ^ (0,5), что b(+0) = 0, sgn А(m(£),£) = sgn(£2 - b(£,)) для всех £е (0,5) х (-5,5). (19)

Так как b '( ^£ . ) = ^- h ; ^{( £} )/ h ; ₂ ( ^£ )| ^ 2 = b ( _{£ 0} , то с учетом ⁽¹⁶⁾ имеем

^А £ , ( x , ^£ )

b '( £ 1 ) = -

А £ ₂( x , £ ) x = m ^{( £} ), ^£ 2 = b ^{( £} 1 )

Из (7) получаем А £ ( x , £ ) = - ( x - £ ₂)² - 2 £ 1 ( x - £ ₂)³ + p ( x , £ )( x - £ ₂)⁴, где p ( x , £ )- ограниченная функция. Отсюда и из оценки (14) при u = m( £ ) следует, что числитель в (20) стремится к нулю при £ 1 ^+ 0. Учитывая (10), из (20) получаем b ' ( + 0) = 0.

Из равенства А ( £ ₂, £ ) = £ ₂, (9), (16) и (19) и леммы получаем следующие утверждения:

При £ еВ 1 = (0, 5 ) х {0} и £е (0, 5 ) х ( - 5 ,0) функция А ( - , £ ) имеет на ( £ ₂, x ) единственный нуль x 1 ( £ ) е ( m( £ ), x ), А X ( x 1 ( £ ), £ ) > 0. Дугу J _£ пересекают единственная периодическая траектория поля X T ( _£ ) - устойчивый грубый предельный цикл, проходящий через точку ( x 1 ( £ ),0).

При £ еЕ 1 , где E 1 : = { £ : 0 <  £ ₂ <  b ( £ 1 ), 0 < £ 1 < 5 }, функция А ( - , £ ) имеет на ( £ ₂, x ) два нуля x ₂( £ ) < x 1 ( £ ), в которых А X ( x₂( £ ), £ ) < 0, А X ( x 1 ( £ ), £ ) >  0. Дугу J _£ пересекают ровно две периодические траектории поля X T ( _£ ) - неустойчивый и устойчивый грубые предельные циклы, проходящие соответственно через точки ( x ₂( £ ),0) и ( x 1 ( £ ),0).

При £ еВ ₂, где В ₂ : = { £ : £ ₂ = b ( £ 1 ), 0 < £ 1 < 5 }, функция А ( - , £ ) имеет на ( £ ₂, x ) единственный нуль m ( £ ), в котором А X ( m ( £ ), £ ) = 0, А'^ ( m (£ ), £ ) >  0. Дугу J _£ пересекает единственная периодическая траектория поля X T ( _£ ) - двойной цикл.

При b ( £ 1 ) <  £ ₂ <  5 поле X T ( _£ ) не имеет периодических траекторий.

Пусть теперь ε ∈ ( - δ ,0] × ( - δ , δ ). Из (8) следует, что δ можно считать столь малым, что ∆′ _x ( x , ε ) > 0 для всех x ∈ ( ε ₂, x ). Отсюда, из равенства ∆ ( ε ₂, ε ) = ε ₂, (9) и леммы получаем следующие утверждения:

При ε ∈ ( - δ ,0] × ( - δ ,0) функция ∆ ( ⋅ , ε ) имеет на ( ε ₂, x ) единственный нуль, а дугу J ε пересекает единственная периодическая траектория – устойчивый грубый предельный цикл.

При ε ∈ ( - δ ,0] × (0, δ ) и ε ∈ B ₃ = ( - δ ,0) × {0} ∆ ( x , ε ) > 0 для всех x ∈ ( ε ₂, x ), а поле X _{T (} ε ₎ не имеет периодических траекторий.

Таким образом, при всех ε ∈ ( - δ , δ )² поле X _{T (} ε ₎ имеет особые точки и периодические траектории, описанные в формулировке теоремы. Поведение остальных траекторий ими определяется однозначно.

Доказательство теоремы 2 закончено.

Заключение

В работе описаны бифуркации рождения периодических траекторий из сшитого фокуса центрально симметричного кусочно-гладкого векторного поля при одно- и двухпараметрических возмущениях общего положения в пространстве векторных полей с такой симметрией. Условия общего положения выписаны в явном виде через коэффициенты разложений компонент векторных полей по степеням фазовых переменных и параметров. Результаты могут быть полезны для нахождения автоколебаний в релейных системах автоматического управления.