Бифуркация точности мехатронных манипуляционных систем при захватывании на ходу

Появление и развитие качественно новых функциональных структур, таких как мехатронные манипуляционные системы (ММС), осознается как результат целенаправленных усилий по их синтезу, выявлению состава их функционально-компоновочных структур, идентификации их характеристик, расширению и усложнению функциональных возможностей, как модулей, так и всей структуры в целом, посредством их перехода на новые технологии реализации.

Практически в любой реальной системе возникает явление самоорганизации при превышении некой пороговой величины приложения внешних организующих (управляющих) воздействий, приводя тем самым к спонтанному качественному изменению состава и поведения системы.

Характер изменений в системе предопределяется уровнем рассмотрения системы и ее особенностей в ходе функционирования, причем чаще всего изменения могут проявляться либо в виде бистабильного перехода к качественно новому состоянию при сохранении однородности поведения системы и ее предсказуемости, либо в виде бифуркационного перехода к принципиально новой элементной и поведенческой организации.

Вышесказанное в полной мере относится к ММС на любом уровне их рассмотрения. Именно в этом аспекте следует рассматривать специальную формулировку понятия мехатроники [1]: «мехатроника изучает синергетическое объединение узлов точной механики с электронными, электротехническими и компьютерными компонентами с целью проектирования и производства качественно новых модулей, систем, машин и комплексов машин с интеллектуальным управлением их функциональными движениями».

Бифуркационные явления, присущие для некоторых параметрических характеристик ММС, подробно рассмотрены в работе [2], где на многочисленных примерах дана характерная иллюстрация количественной и качественной сторон этого. В настоящей работе ограничимся анализом бифуркации точностных параметров, характерных для дистанционного захвата объектов ММС на ходу.

Бифуркация точностных показателей двухзвенного манипулятора

Задача точностного анализа состоит в исследовании точности исполнительных механизмов с учетом влияния факторов, определяющих их точностные характеристики, включая вопросы задания и анализа влияния первичных погрешностей на выходную точность ММС.

Первичные погрешности всегда являются неопределенными, и для их описания применимы следующие модели:

• 1.    Погрешности заданы интервалами возможных их вариаций со строго ограниченными и известными предельными значениями. При таком представлении возможны как детерминированные, так и вероятностные модели точностного описания ММС .

• 2.    Задание областей неопределенности эллипсоидами, что также мож-

• но связать как с детерминированными, так и с вероятностными моделями. Причем в детерминированном случае эллипсоид есть результат аппроксимации реальной, более сложной по форме области неопределенности, а в вероятностном случае эллипсоид представляет собой поверхности равных значений плотностей вероятностей при гауссовском распределении.

Алгоритмы вычислений точности ММС в детерминированной и вероятностной постановках и их взаимосвязь представлены в работе [3].

Номинальное положение полюса C захвата ММС определяется зависимостью ^ * = ^ * ( q ) , где q = [ q₁,q ₂,..., q n ] т — вектор-столбец обобщенных координат. Ими являются длины l i звеньев и межзвенные углы Ф _i, i = 1, 2, . . , n . Рассматривая значения ошибок A q i в шарнирах O i для конфигураций q е Q = { q i' <  q i <  q " } можно оценить точность ММС.

Погрешность позиционирования ММС в точке ^ будет „ d r *

A = A £ = — = A ( q , r ) A q .

d q

При ее оценке следует пользоваться скаляром

A ² =| A z | ² = A q ^т A ^т A A q = A q ^т Ф A q .

Анализ точности ММС сводится к задаче квадратичного программирования в области задания A q eA Q .

При детерминированной постановке области задания первичных ошибок A q могут быть представлены в виде:

• -    параллелепипеда A Q = { A q : 5' i <  q i <  J i "}, i = 1,2,..., n ;

• -    эллипсоида A q ^т R A q = 1, где R — диагональная матрица предельных допусков на A q .

При вероятностном анализе задается вероятностная плотность распределения погрешности в каждом шарнире f ( A ^ i ), i = 1,2,..., n . Затем определяется плотность распределения погрешности позиционирова-ния f ( A r ) = f ( A x , A y , A z ) = (2n ) ^{- 3/2} К ^1/2exp ( - 0.5 A ^т К A ), где К — корреляционная матрица размером 3*3 системы случайных величин A x , A y , A z ее диагональные элементы — это их дисперсии, внедиагональные — корреляционные моменты; ее след Sp 11 K 11 = D = D_x + D y + D_z . Стоящая под знаком экспоненты квадратичная форма от A x , A y , A z принимает постоянные значения на поверхности некоторого эллипсоида, характеризующего форму и размеры окрестности номинального позиционирования, куда с определенной вероятностью p попадает захват ММС.

Для иллюстрации проявления бифуркации параметров точности ММС ограничимся вероятностным подходом на примере двухзвенного шарнирно-рычажного манипулятора (рис. 1).

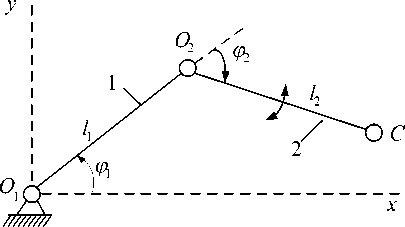
Рис. 1. Двухзвенный шарнирно-рычажный манипулятор

Декартовы координаты воспроизводящей точки С будут x = l ₁cos ϕ ₁ + l ₂cos( ϕ ₁ + ϕ ₂), y = l ₁sin ϕ ₁ + l ₂sin( ϕ ₁ + ϕ ₂).

Проводя ось x через точку C , имеем y = 0 , далее, используя безразмерные величины ξ , η , имеем:

ξ=cosϕ1+εcos(ϕ1+ϕ2), ξ=x, l1

η = sin ϕ + ε sin( ϕ + ϕ ) = 0, ε = ^{l 2} .

• 1       12         _{l 1}

Величина ξ есть расстояние от точки крепления O до полюса схвата C и меняется в пределах I 1 - ε ≤ ξ ≤ 1 + ε .

На практике при оценке точности погрешность позиционирования удобно характеризовать величиной большей полуоси эллипса неопределенности вместе с указанием доверительной вероятности. Метод удобен при оценке точности ММС на стадии проектирования, когда для партии создаваемых ММС ошибки паспорта и ошибки управления можно считать случайными.

Из безразмерных декартовых координат полюса C схвата (рис. 1) ξ = cos ϕ ₁ + ε cos( ϕ ₁ + ϕ ₂),          xl y

ξ = , ε = ² , η = η = sin ϕ ₁ + ε sin( ϕ ₁ + ϕ ₂) = 0,        l ₁ l ₁ l ₁

при малых значениях ∆ ϕ ₁ и ∆ ϕ ₂ следует

∆ξ=-η∆ϕ1-εsin(ϕ1+ϕ2)∆ϕ2,

∆η=ξ∆ϕ1+εcos(ϕ1+ϕ2)∆ϕ2

откуда получаются элементы корреляционной матрицы K в виде: D ξ = (4 ξ ² ) ^{- 1} ( ξ m²ax - ξ ² )( ξ ² - ξ m²in ) D 2 ,

Dη=r2D1+(4ξ2)-1(ξ2-ξ*2)D2,D1,2 = D(ϕ1ϕ2), а корреляционный момент представить так:

K ξη = (4 ξ ² ) ^{- 1} ( ξ ² - ξ *² )( ξ m²ax - ξ ² )( ξ ² - ξ m²in ) D 1,2 .

Ориентация эллипсоида равных вероятностей (э.р.в.) определяется зависимостью tg2θ = 2 K ξη /( D ξ - D η ), где θ — угол наклона большой полуоси к оси O ξ .

Из анализа следует наличие критического отношения дисперсий d = d ^* = ε ² /1 - ε ² ,определяющего бифуркацию параметров э.р.в. На рис.

• 2    показана бифуркация параметров э.р.в. ( a — эволюция э.р.в. при d < d _* ; δ — эволюция э.р.в. при d ≥ d _*). Из рис. 2 видно, что с ростом ξ при d < d _* э.р.в. поворачивается против часовой стрелки, а при d ≥ d _* э.р.в.

покачивается относительно вертикали.

а)

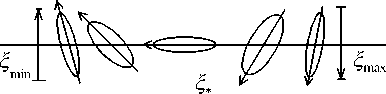
d < d

∗

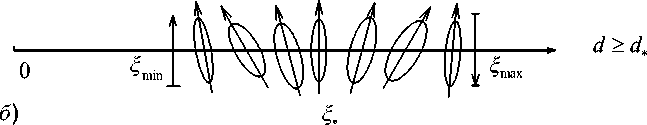
Рис. 2. Бифуркация параметров эллипса рассеяния

Бифуркация параметров при захватывании объекта захватным устройством дистанционного действия

При исследовании механики циклоидальных манипуляторов [4] возникает задача захватывания объекта «на ходу». Сложность обеспечения надежного захватывания объекта захватным устройством циклоидального манипулятора заключается в том, что остановка на заданной позиции является мгновенной. Поскольку реально никакое захватное устройство мгновенно срабатывать не может, то это означает, что захватывание вынужденно происходит во время движения. При захватывании «на ходу» могут использоваться захватные устройства, построенные на различных физических принципах. Встречаются ситуации, когда целесообразно использовать захватные устройства, обладающие свойством неконтактного воздействия на захватываемый объект, обладающие дальнодействием, например, для захватывания плоских деталей или заготовок с горизонтальной поверхности. При захватывании таких объектов не нужно опускать захватное устройство вниз до возникновения контакта с объектом, достаточно подвести его по горизонтали с сохранением значительного зазора (рис. 3), при срабатывании объект притягивается вверх и прилипает к захватному устройству. Тем самым из механизма манипулятора исключается механизм вертикального перемещения, что содействует повышению надежности.

a

v

С

F тр             _{R              D}

G

x

Х^

Рис. 3. Схема для расчета захватного устройства

Вблизи точки мгновенной остановки движение рабочего органа можно представить как прямолинейное по радиальному направлению (перемещения в поперечном направлении на порядок меньше). Поэтому указанную вертикальную плоскость следует выбрать также радиальной, именно в ней и будет происходить движение.

Захватное устройство и объект идеализированно представлены в виде точек, между которыми имеется сила дистанционного взаимодействия, причем первой точкой считается центр C масс объекта, а второй — центр D нижней части захватного устройства.

Выражение для модуля силы взаимодействия можно записать следующим образом:

R(У) = -Ar, У = и - x, У где у — расстояние между точками C и D, и — координата точки C

(захватываемого объекта), x — координата точки D (схвата). Первая величина учитывает изменение силы с расстоянием (для всех реальных устройств с увеличением расстояния эта сила всегда убывает).

Дифференциальное уравнение динамики для описанной модели имеет вид:

mХ = - F +

A

( и - x ) ²

где m — масса объекта, F — сила трения о плоскость, и — закон перемещения захватного устройства по координате x .

В соответствии с приближенным движением вблизи точки возврата G концевой точки D циклоидального механизма движение по радиальной координате можно считать равноускоренным, так что

, х                 w«t²

и (t) = и 0 + v01 + —°— где и0, v0, w0 — положение, скорость движения и ускорение схвата в момент включения притягивающего устройства.

Поскольку скорость перемещения захватного устройства в точке G достигает нуля полагаем v ₀ =±^ 2 w ₀ и ₀ , где w ₀ ~ 3 о_х 1 112 (здесь ю _х — угловая скорость первого звена циклоидального манипулятора, l ₁ — его длина).

Отсчет времени ведется от момента включения притягивающего уст- ройства захвата. Так как x=u - у , дифференциальное уравнение в относительном движении будет

A mу =—2 + F + mw0.                 (1)

У

Начальные условия записываются исходя из предположения, что в начальный момент времени объект находился в покое на расстоянии x ₀ от точки G . Тогда у ₀ = u ₀ - x ₀.

Таким образом, для решения рассматриваемой задачи необходимо ввести начальное положение объекта x ₀ , начальное положение схвата u ₀ , ускорение схвата w ₀, параметр притягивающей силы A , силу трения F, массу объекта, знак скорости (направление движения схвата). Так как схват может находиться как левее, так и правее объекта, он может двигаться как вправо, так и влево.

Абсолютная скорость схвата определяется его местоположением U₀ =±^ 2 au ₀ .

При этом возможны следующие ситуации:

• а )    У о >  0, U ₀ <  0, схват приближается к объекту справа с замедлением

• б )    у ₀ <  0, U ₀ <  0, удаляется от объекта влево от него с замедлением

• в )    У ₀ >  0, U ₀ >  0, удаляется вправо от него с ускорением

• г )    У ₀ <  0, U ₀ >  0, приближается к объекту слева с ускорением .

Ясно, что движение покоящегося объекта может начаться только в случае превосходства силы трения, действующей на него притягивающей силой схвата, т. е. когда R >  F . Так как сила притягивания схвата увеличивается при приближении к объекту, то существует радиус окрестности объекта, в котором происходит взаимодействие схвата с объектом. Назовем эту окрестность «действенной» и ее радиус обозначим у * , где

• ^У * =       .

Рассмотрим подробнее перечисленные случаи:

• а )    Если у ₀ >  у * , то объект неподвижен до момента вхождения схвата в действенную зону t * , а затем начинает движение до момента захватывания его в момент t * +A t ;

Если у ₀ <  у * , то объект сразу движется до встречи в момент времени A t .

• б )    Если | у ₀1 > у * , то объект покоится до момента движения схвата до точки и = 0 и обратно до точки x ₀ - у * , и случай б ) переходит в случай г ).

Если | у ₀1 < у * , то объект сразу начинает двигаться и далее может догнать схват или остановиться.

• в )    Если у ₀ >  у * , то объект останется на месте.

Если у0 < у*, то объект сразу сдвинется с места, но может догнать схват или остановиться.

• г )    Если | у ₀ | > у * , то объект вначале покоится, а затем с ускорением

движется влево до встречи со схватом.

При вхождении или нахождении схвата в действенной зоне объекта необходимо решать уравнение (1) для следующих начальных условий:

при t = t H ,    у = У н и ^у = ^{у                          (2)}

Если у _н <  0 (случаи а), г)), то идет их сближение (в это время схват находится в действенной зоне) и захватывание неизбежно.

Если у _н >  0 (случаи б), в)), то в этом случае объект движется вслед схвату и может либо догнать его, либо отстать окончательно и остановиться. Для успешного захватывания необходимо, чтобы в последующем у стало отрицательным. Выясним, при каких условиях это возможно.

Проинтегрировав уравнение (1) с начальными данными (2), получим:

у ² ( у ) = 2 к , у + —2 + 2 D , ^y

F , A _ у2

к ₂

—

.

y _н

где к, = W0 +— , к2 =— , D =   - к,ун mm 2

Для того чтобы в какой-то момент времени относительная скорость сближения у поменяла свой знак, необходимо выполнение равенства к,у2 + Оу + к2 = 0, а это возможно, только когда D2 - 4к, к2 > 0 или

| D | >  2 4 к, к ₂

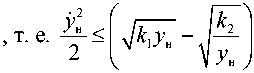
у- ² либо —

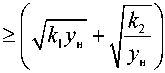
. Объект

перестает отставать от схвата и начинает его догонять в момент времени , - D ± J D ² - 4 к , к ₂

когда у ,, ₂ =--------2 ^---------.

Фазовый портрет этого уравнения приведен на рис. 4.

Из рис. 4 видно, что успешное захватывание при уходе схвата от захватываемого объекта в случае в) будет происходить при условии:

Ун <

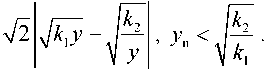
Область фазовой плоскости, соответствующая этим условиям, показа- на на рис. 4 штриховкой.

Для случая б) при выполнении условий ун > V2 V- к1 ун

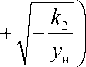
D у! < у < у2, у, >--- произойдет благополучный захват, когда еще схват

• ¹    ни Z.          2 к ,

не достигнет точки возврата. Иначе, как указано выше, этот случай перейдет в случай г).

Выявлено, что в этом процессе существует точка бифуркации в зави- симости от параметра D. Здесь D =--^(mw + F)A.

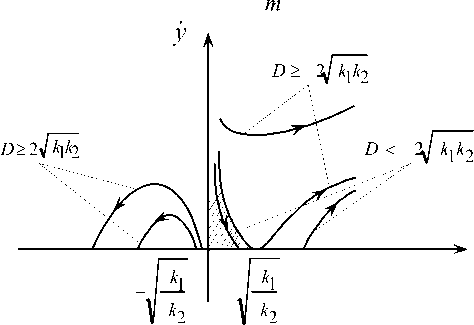
Рис. 4. Фазовый портрет уравнения движения

Заключение

Выявленный факт бифуркации кинематической точности двухзвенного шарнирного манипулятора в рабочей зоне указывает на взаимосвязь его геометрических параметров и первичных ошибок механизма в пределах их вариации, что дает информацию для синтеза и эксплуатации таких механизмов. Кроме того, проведенное исследование позволяет обоснованно назначать допуски на характеристики манипулятора.

Детальный анализ процесса захватывания объекта с учетом инерционности объекта с ходу позволил получить оценки динамической точности на простейших геометрических представлениях, впервые сформулированных авторами. Было выяснено, что объект начинает движение, как только сила притягивания объекта к схвату начнет превосходить сумму сил инерции покоя объекта и силы трения, действующей на него. Конкретный эффект предлагаемой модели должен быть экспериментально апробирован при отработке приводов реального манипулятора.