Центральные элементы треугольника и пирамиды Паскаля, интерпретации и соотношения

Одними из важнейших комбинаторных структур, которые находят широкое применение в различных областях математики, информатики и анализе данных, являются треугольник и пирамида Паскаля [2] . Каждая из них представляет собой мощный инструмент для решения задач, связанных с комбинаторикой, алгоритмизацией и оптимизацией. Центральные элементы этих структур, такие как центральные биномиальные коэффициенты в треугольнике Паскаля, обладают уникальными свойствами, которые делают их полезными для анализа путей на целочисленных сетках, моделирования вероятностных процессов [1] и разработки криптографических алгоритмов. Центральные триномиальные коэффициенты позволяют эффективно подсчитывать количество путей в трехмерных сетках, что имеет важное значение для задач оптимизации маршрутов и анализа данных. Кроме того, как и треугольник Паскаля, пирамида Паскаля может служить основой для создания сложных криптографических схем, обеспечивая высокую степень защиты информации благодаря своим комбинаторным свойствам. В данной статье рассматриваются некоторые геометрические свойства этих структур, а также их возможные приложения и перспективы дальнейших исследований.

1 Треугольник и пирамида Паскаля

Треугольник Паскаля — это классическая комбинаторная структура, которая представляет собой бесконечный треугольный массив чисел (рис. 1), где каждый элемент равен сумме двух элементов, расположенных над ним слева и справа в предшествующей строке, т. е. для целых неотрицательных n, к удовлетворяет рекуррентному соотношению (правилу Паскаля) [3] :

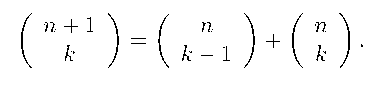
n + 1 к к - 1   + к nn с начальными условиями

n

= 0; и = 0, если mm(n, k,n — к) < 0, а также граничным условиям

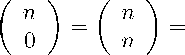
и равенству симметрии относительно центральной оси n k

n - k

Элементы Q) = щп-ку, треугольника Паскаля соответствуют биномиальным коэффициентам, то есть коэффициентам разложения степе- ни бинома:

n

( X + «■ = X П k =0 '

x ^k

что является полезным инструментом для решения задач, связанных с комбинаторикой и вероятностью.

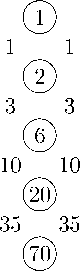
15    61

21    71

56   28    81

n

Рис. 1. Треугольник Паскаля

Пирамида Паскаля является трехмерным обобщением треугольника Паскаля. В этой структуре элементы располагаются в виде бесконечной трехгранной пирамиды (рис. 2), где каждый элемент равен сумме трех элементов, расположенных над ним в предыдущем слое, т. е. для целых неотрицательных n, k , l удовлетворяет рекуррентному соотношению [2] :

n+1        n          n        n k, l = k - 1, l + k, l - 1   + k, l при выполнении начальных условий:

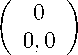
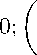
n k, l

= 0 , если min( n, k, l, n - k - l ) <  0 ,

граничных условий:

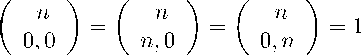
и равенств симметрии в каждом слое [2] :

n

k, l

n l, k

n

n

n

- k - l,l

k, n

- k - l

Числа к^ = _fc, 1 !( П — _к-]у называются триномиальными коэффициентами, то есть коэффициентами разложения степени тринома:

n n - k

( x + y + 1) ^п = ЕЕ kl x k y ^l , k=0 l=0      ^, '

что позволяет обрабатывать многомерные данные, моделировать сложные системы, где требуется учитывать взаимодействие между несколькими переменными.

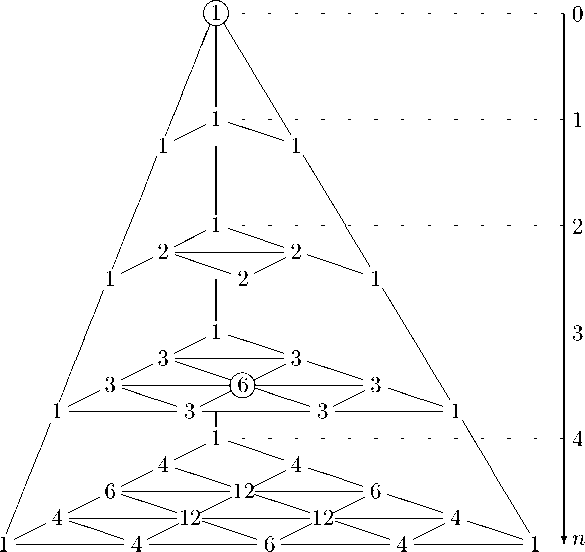
Рис. 2. Пирамида Паскаля

2    Пути на целочисленной сетке

Треугольник и пирамида Паскаля тесно связаны с задачами подсчета путей на целочисленной сетке [2] . Рассмотрим каждую из этих структур подробнее.

Треугольник Паскаля напрямую связан с задачей подсчета путей в двумерной целочисленной сетке. Рассмотрим сетку, где можно перемещаться только вправо или вверх, выполняя шаги (1;0) или (0; 1) (рис. 3). Путь из точки (0; 0) в точку ( n ; к ) можно представить как последовательность таких шагов.

Утверждение 1. Количество путей длины n + к в сетке n х к от (0; 0) до ( n ; к ) с использованием шагов (1;0) и (0; 1) равно биномиальному коэффициенту ( n+k ) .

Этот коэффициент можно найти в треугольнике Паскаля в строке с номером n + к на к-й позиции, n G { 0 , 1 , 2 ,... } , к G { 0 , 1 , 2 ,... } .

(0;0)

Рис. 3. Путь на двумерной целочисленной сетке

Например, количество путей из точки (0; 0) в точку (2; 2) равно (2) =6 , что соответствует элементу треугольника Паскаля на четвертой строке и второй позиции (рис. 1).

Пирамида Паскаля обобщает эту концепцию на трехмерную сетку. В трехмерной сетке можно перемещаться в трех направлениях: вправо, вверх и в глубину. Путь из точки (0; 0; 0) в точку ( n ; к ; 1 ) можно представить как последовательность шагов в этих трех направлениях.

Утверждение 2. Количество путей длины n + к + 1 в сетке n х к х l от (0; 0; 0) до ( n ; к ; l ) с использованием шагов (1; 0; 0) , (0; 1; 0) и (0; 0; 1) равно триномиальному коэффициенту ( n+k+l ) •

Этот коэффициент можно найти в пирамиде Паскаля в горизонтальном слое с номером n + к + 1 на к-й горизонтальной позиции и l-й вертикальной позиции, n G { 0 , 1 , 2 ,... } , к G { 0 , 1 , 2 ,... } , l G { 0 , 1 , 2 ,... } .

Например, количество путей из точки (0; 0; 0) в точку (1; 1; 1) равно (Д) = 6 , что соответствует элементу пирамиды Паскаля в третьем горизонтальном слое на 1-й горизонтальной и 1-й вертикальной позиции (рис. 2).

3    Центральные элементы

Центральные элементы треугольника и пирамиды Паскаля представляют собой важные комбинаторные объекты, которые находят применение в различных областях математики и информатики. Рассмотрим их подробнее.

Центральные элементы треугольника Паскаля, также известные как центральные биномиальные коэффициенты, располагаются в середине четных строк треугольника (рис. 1). Эти элементы обозначаются как ( 2n ) = (п)! и представляют собой количество способов выбрать n из 2 n различных элементов.

Центральные элементы пирамиды Паскаля располагаются в слоях, номера которых кратны трем (рис. 2), и представляют собой обобщение центральных биномиальных коэффициентов на трехмерный случай. Эти элементы обозначаются как (3D = (3^ и представляют собой количество способов выбрать n элементов из каждого из трех множеств по n элементов.

Центральные элементы треугольника и пирамиды Паскаля используются для решения задач, связанных с различными двумерными, трехмерными и многомерными комбинаторными структурами, в том числе и подсчетом путей в целочисленных сетках.

Центральные элементы треугольника Паскаля образуют последовательность чисел 1, 2, 6, 20, 70, 252, 924, 3432 ... (A000984 в [4] ) и подсчитывают, согласно утверждению 1, количество путей из точки (0; 0) в точку ( n ; n ) при движении по двумерной целочисленной сетке. Первые 5 чисел этой последовательности обведены на рисунке 1.

Утверждение 3. Количество путей длины 2 п в сетке n х n от (0; 0) до ( n ; n ) с использованием шагов (1;0) и (0; 1) равно биномиальному коэффициенту ( 2 I ).

Центральные элементы пирамиды Паскаля образуют последовательность чисел 1, 6, 90, 1680, 34650, 756756, ... (A006480 в [4] ) и подсчитывают, согласно утверждению 2, количество путей из точки (0; 0; 0) в точку ( n ; n ; n ) при движении по трехмерной целочисленной сетке. Первые два числа указанной последовательности обведены на рисунке 2.

Утверждение 4. Количество путей длины 3 n в сетке n х n х n от (0; 0; 0) до ( n ; n ; n ) с использованием шагов (1; 0; 0) , (0; 1; 0) и (0; 0; 1) равно триномиальному коэффициенту ( ^3п ) .

, I I

4    Сумма квадратов биномиальных коэффициентов и ее обобщение в треугольнике Паскаля

Сумма квадратов биномиальных коэффициентов в n-й строке треугольника Паскаля равна центральному биномиальному коэффициенту, расположенному в строке с номером 2 n. Это известный результат в комбинаторике, который можно доказать несколькими способами. Приведем новое доказательство через подсчет путей на целочисленной сетке и покажем, как это соотношение возникает естественным образом. Этот подход продемонстрирует глубокую связь между комбинаторикой и геометрией, а также позволит обобщить рассматриваемое тождество на триномиальные коэффициенты.

Теорема 1. Для любого неотрицательного целого числа n выполняется равенство:

X ( n ) ² = ( ² n ) .                   (4)

kn

• k=0 ^{v 7 v} '

Доказательство.

Рассмотрим целочисленную сетку размером n х n. Количество путей из точки (0; 0) в точку ( n ; n ) , состоящих из n шагов вправо и n шагов вверх, согласно утверждению 3, равно (2^). С другой стороны, можно разбить этот путь на два, равных по количеству шагов, этапа:

• 1)    сначала выполнить n шагов, при этом k шагов вправо и n — k шагов вверх;

• 2)    затем выполнить еще n шагов, при этом остается n — k шагов вправо и n — ( n — k ) = k шагов вверх.

Количество способов прохождения первого этапа равно ⁿ _k , а второго этапа соответственно равно _n- ⁿ _k . Таким образом, число способов выполнения по очереди обоих этапов равно их произведению ⁿ _{k n-} ⁿ _k .

Поскольку на первом этапе в целочисленной сетке размером n х n можно выполнить 0 <  k <  n шагов вправо, то, суммируя все способы, получаем общее число путей из точки (0; 0) в точку ( n ; n ) за два этапа:

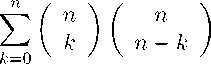
Сравнивая общее количество путей, полученное согласно утверждению 3 и рассчитанное нами за два этапа, имеем:

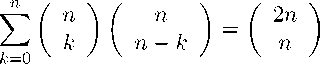
Принимая во внимание равенство симметрии (2) , получаем равенство (4) . Теорема доказана.

Рассуждая аналогично, путь можно разбить на два, не обязательно равных по количеству шагов, этапа. Получаем обобщение равенств (4) и (5) для биномиальных коэффициентов.

Теорема 2. Для любых неотрицательных целых чисел n и m, при m <  n , выполняется равенство:

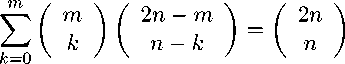
Доказательство.

Доказательство проведем аналогично теореме 1, рассматривая пути на целочисленной сетке размером n х п. Количество путей из точки (0; 0) в точку ( п ; п ) , состоящих из п шагов вправо и п шагов вверх (итого 2 п шагов), согласно утверждению 3, равно ( 2 П ). Получили правую часть равенства.

Левую часть равенства можно получить, разбивая этот путь на два этапа:

• 1)    сначала выполнить m шагов, где m <  п, при этом k шагов вправо и m — k шагов вверх;

• 2)    затем выполнить еще 2 п — m шагов, при этом остается п — k шагов вправо и п — ( m — k ) = п — m + k шагов вверх.

Количество способов прохождения первого этапа равно ^m _k , а вто- 2 n - m рого этапа соответственно равно _n ⁿ _-k ^m .

Таким образом, число способов выполнения по очереди обоих этапов m 2 n - m равно их произведению _{k n-k} .

Поскольку на первом этапе можно выполнить 0 <  k <  m шагов вправо, то, суммируя все способы, получаем общее число путей из точки (0; 0) в точку ( п ; п ) за два этапа, не равных по количеству шагов, т. е. левую часть равенства. Теорема доказана.

Представляет интерес геометрическая интерпретация равенств (4) , (5) и (6) в треугольнике Паскаля. Каждое из них описывает способы получения центрального элемента 2 п -й строки треугольника Паскаля:

• 1)    согласно равенству (4) нужно:

• -    наложить элементы n -й строки на элементы этой же n -й строки;

• -    наложенные элементы между собой перемножить;

• -    сложить полученные произведения;

• 2)    согласно равенству (5) нужно:

• -    наложить элементы n -й строки на элементы этой же n -й строки в обратном порядке, т. е. повернув ее на 180 градусов относительно центра этой строки;

• -    наложенные элементы между собой перемножить;

• -    сложить полученные произведения;

• 3)    согласно равенству (6) нужно:

• -    наложить элементы произвольной строки с номером m на элементы строки с номером 2 n — m в обратном порядке, т. е. повернув ее на 180 градусов относительно центра этой строки;

• -    наложенные элементы между собой перемножить;

• -    сложить полученные произведения.

Обратные наложения во втором и третьем случаях также верны, согласно равенству симметрии (2) , т. е. если поворачивать накладываемую строку на 180 градусов, а ту строку, на которую происходит наложение, оставлять на месте, результат не изменится. А можно поворачивать обе строки на 180 градусов, а затем производить наложение, согласно тому же равенству симметрии (2) , результат останется прежним. Приведем пример.

Пример 1. Рассмотрим центральный элемент 70 , находящийся в строке с номером 2 п = 8 (рис. 1). Этот элемент можно получить несколькими способами:

• 1)    согласно равенствам (4) и (5) этот элемент можно получить путем наложения на строку с номером n = 4 этой же строки в прямом или перевернутом на 180 градусов положении относительно ее центра:

70 = 12 + 42 + 62 + 42 + 12;

• 2)    согласно равенству (6) этот элемент можно получить путем наложения в прямом или перевернутом на 180 градусов, относительно ее центра, положении, строки с номером 0 на строку с номером 8 :

70 = 1 • 70, или путем наложения строки с номером 1 на строку с номером 7, что согласуется с правилом Паскаля (1) :

70 = 1 • 35 + 1 • 35, или путем наложения строки с номером 2 на строку с номером 6:

70 = 1 • 15 + 2 • 20 + 1 • 15, или путем наложения строки с номером 3 на строку с номером 5:

70 = 1 • 5 + 3 • 10 + 3 • 10 + 1 • 5, или путем наложения строки с номером 4 на строку с номером 4:

70 = 1 • 1 + 4 • 4 + 6 • 6 + 4 • 4 + 1 • 1 .

Результаты, полученные в теоремах 1 и 2, можно обобщить на триномиальные коэффициенты, что позволяет расширить область применения комбинаторных методов в различных математических и прикладных задачах.

5 Сумма квадратов биномиальных коэффициентов и ее обобщения в пирамиде Паскаля

Проведя серию вычислений, мы установили, что равенство (4) не имеет прямого обобщения на триномиальные и полиномиальные коэффициенты. Приведем пример.

Пример 2. Рассмотрим центральный элемент 6 , находящийся в слое с номером 3 п = 3 (рис. 2). Проверим, можно ли этот элемент получить, суммируя квадраты элементов слоя с номером n = 1 .

Имеем:

1            /1            /1( 0, о) +(с, 1) +(1, о) = 12+ 12+ 12 = 3 = 6, что показывает отсутствие прямого обобщения равенства (4) на триномиальные коэффициенты.

Проверим, можно ли этот элемент получить, суммируя третьи степени элементов слоя с номером n = 1 :

Имеем:

( о, о) +(о, 1) +(1,о) =13 + 13 + 13 = 3 = 6- что еще раз показывает отсутствие прямого обобщения равенства (4) на триномиальные коэффициенты.

Несмотря на это равенства (5) и (6) имеют обобщения для триномиальных коэффициентов. Сначала приведем и докажем обобщение равенства (5) .

Теорема 3. Для любого неотрицательного целого числа n выполняется равенство:

n n - k

2n

k =0 l =0

n — k,n — I

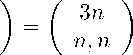
Доказательство.

Доказательство проведем рассматривая пути на целочисленной сетке размером n х n х n. Количество путей из точки (о; о; о) в точку ( n ; n ; n ) , состоящих из n шагов вправо, n шагов вверх и n шагов в глубину (итого 3 n шагов), согласно утверждению 4, равно (,3”), что дает нам правую часть равенства.

Левую часть равенства можно получить разбивая этот путь на два этапа:

• 1)    сначала выполнить n шагов, при этом k шагов вправо, l шагов вверх и n — k — l шагов в глубину;

• 2)    затем выполнить еще 2 n шагов, при этом остается n — к шагов вправо, n — l шагов вверх и n — ( n — к — l ) = к + 1 шагов в глубину.

Количество способов прохождения первого этапа равно _k ⁿ _l , а вто- 2 n рого этапа соответственно равно _n-k,n-l .

Таким образом, число способов выполнения по очереди обоих этапов равно их произведению (^(n^n-i).

Поскольку на первом этапе можно выполнить 0 <  к <  n шагов вправо и 0 <  l <  n — к шагов вверх, то, суммируя все способы, получаем общее число путей из точки (0; 0; 0) в точку ( n ; n ; n ) за два этапа, т. е. левую часть равенства. Теорема доказана.

А теперь приведем и докажем обобщение равенства (6) для триномиальных коэффициентов.

Теорема 4. Для любых неотрицательных целых чисел n и m , при m <  n , выполняется равенство:

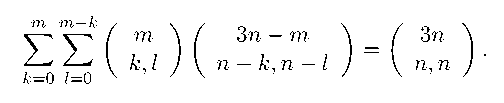
m m - k

3 n — m n — k,n — l

3 n

m n, n

Доказательство.

Доказательство проведем аналогично доказательству теоремы 3, рассматривая пути на целочисленной сетке размером n x n x n. Количество путей из точки (0; 0; 0) в точку ( n ; n ; n ) , состоящих из n шагов вправо, n шагов вверх и n шагов в глубину (итого 3 n шагов), согласно утверждению 4, равно _n ³ _, ⁿ _n , что дает нам правую часть равенства.

Левую часть равенства можно получить разбивая этот путь на два этапа:

• 1)    сначала выполнить m шагов, при этом k шагов вправо, l шагов вверх и m — к — l шагов в глубину;

• 2)    затем выполнить еще 3 n — m шагов, при этом остается n — к шагов вправо, n — l шагов вверх и n — ( m — к — l ) = n — m + к + l шагов в глубину.

Количество способов прохождения первого этапа равно _k ^m _l , а второго этапа соответственно равно _n ³ _- ⁿ _k ^- _,n ^m _{- l} .

Таким образом, число способов выполнения по очереди обоих этапов m 3 n - m k ^m l n ³- ⁿ k,n ^m - l .

Поскольку на первом этапе можно выполнить 0 < к < m шагов вправо и 0 < l < m — к шагов вверх, то, суммируя все способы, получаем общее число путей из точки (0; 0; 0) в точку (n; n; n) за два рассматриваемых этапа, т. е. левую часть равенства. Теорема доказа- на.

Как и для биномиальных коэффициентов, интересна геометрическая интерпретация равенств (7) и (8) для триномиальных коэффициентов в пирамиде Паскаля. Каждое из них описывает способы получе- ния центрального элемента 3n-го слоя пирамиды Паскаля:

• 1)    согласно равенству (7) нужно наложить элементы n-го слоя на элементы 2 n-го слоя, повернув его на 180 градусов так, чтобы вершины n n       n

(n 07, \o n/ и \0 0/ меньшего треугольника оказались над элементами

(2n ), (2n) и (2n) большего треугольника, наложенные элементы между 0,n , n,0 n,n              ру          ,                               ду собой перемножить и затем сложить полученные произведения;

• 2)    согласно равенству (8) нужно наложить элементы произвольного

слоя с номером m на элементы слоя с номером 3n - m, повернув его на 180 градусов так, чтобы вершины (т0о), (omm) и (/) меньшего тре-

/ 3n-m \ ( 3n-m \ \n-m,n) , \п,—-т/

угольника оказались соответственно над элементами и (3 n /) большего треугольника, наложенные элементы между собой перемножить и затем сложить полученные произведения.

Приведем пример.

Пример 3. Рассмотрим центральный элемент ₃ ¹² ₃ = 34650 , находящийся в горизонтальном слое пирамиды Паскаля с номером 12 .

Согласно равенству (7) этот элемент можно получить путем нало- жения горизонтального слоя с номером 4 на горизонтальный слой с номером 8 в перевернутом на 180 градусов положении (рис. 4):

1    4    6    4    1 /1

\ 4   12  12   4 ./^     88

\ 6   12   6 ./^ 28  5628

\ 4    4            56  168 16856

(n =4)    1 /.^ \70 280 420 28070/

\^//     56 ^^ 280 560 560 280/56

28  168\420  560  420/16828

• 8   56  168\280 280/168  568

1     8    28   5(i70/ 56   28    81

(2 n = 8)

Рис. 4. Наложение перевернутого 4-го слоя на слой номер 8

34650 = 1 · 70 + 4 · 280 + 6 · 420 + 4 · 280 + 1 · 70+

+4 · 280+12 · 560+12 · 560+4 · 280+

+6 · 420+ 12 · 560+6 · 420+

+4 · 280+4 · 280+

+1 · 70 .

Согласно равенству (8) , этот же элемент можно получить путем наложения горизонтального слоя с номером 3 на горизонтальный слой с номером 9 в перевернутом на 180 градусов положении (рис. 5):

1    3    3    1 /1

\ 3   6   3 z^^4     99

\ 3   336  7236

\ 1             84  252 25284

( m = ³⁾\/\      126 504 756 504 126   ⁽³ n - m = 9)

126 \ 630 1260 1260 630 / 126

84  504\ \ 260 1680 126 0/ 504 84

36  252 756/1260 126(/756 252 36

• 9   72  252 504\б30/^/504 252  72   9

1    9    36   84 12\/L26   84   36    9    1

Рис. 5. Наложение перевернутого 3-го слоя на слой номер 9

34650 = 1 · 630+3 · 1260+3 · 1260 + 1 · 630+

+3 · 1260 + 6 · 1680 + 3 · 1260+

+3 · 1260 + 3 · 1260+

+1 · 630, или путем наложения горизонтального слоя с номером 2 на горизонтальный слой с номером 10 в перевернутом на 180 градусов положении:

34650 = 1 · 3150 + 2 · 4200 + 1 · 3150+

+2 · 4200 + 2 · 4200+

+1 · 3150, или путем наложения горизонтального слоя с номером 1 на горизонтальный слой с номером 11 в перевернутом на 180 градусов положении, что согласуется с известной формулой (3):

34650 = 1 · 11550 + 1 · 11550++1 • 11550, или путем наложения горизонтального слоя с номером 0 на горизонтальный слой с номером 12 в перевернутом на 180 градусов положении:

34650 = 1 •34650.Заключение

В данной работе исследовались некоторые геометрические свойства центральных элементов треугольника и пирамиды Паскаля. Были получены выражения центральных биномиальных коэффициентов через суммы произведений элементов строк треугольника Паскаля и центральных триномиальных коэффициентов через суммы произведений элементов слоев пирамиды Паскаля соответственно, которые обобщают известное равенство о сумме квадратов биномиальных коэффициентов, а также рекуррентные соотношения на основе правила Паскаля. В силу приведенного геометрического алгоритма их получения доказанные равенства могут служить основой сложных многоуровневых криптографических схем и процедур сжатия больших объемов данных. Для иллюстрации технологии выполнения произведений приведены подробные примеры. Дальнейшее исследование предполагает рассмотрение обобщений полученных равенств на гиперпирамиды Паскаля, а также изучение взаимосвязей других частей треугольника, пирамиды и гиперпирамид Паскаля.