Численно-аналитическая модель для интерпретации результатов индикаторных исследований нефтяных пластов: решение прямой задачи при наличии каналов низкого фильтрационного сопротивления
Автор: Федоров К.М., Гильманов А.Я., Шевелв А.П., Изотов А.А., Кобяшев А.В.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 1 т.17, 2024 года.
Бесплатный доступ
Рассматривается проблема интерпретации индикаторных (трассерных) исследований нефтяных пластов, в которые через нагнетательную скважину закачивается помеченное химическое вещество - трассер - для слежения за течением и замеряется его концентрация в окружающих добывающих скважинах. Промысловые сведения свидетельствуют, что в пласте имеются каналы низкого фильтрационного сопротивления, по которым трассер движется со скоростями, на несколько порядков превышающими скорость его фильтрации. Природа и свойства этих каналов неизвестны, для их изучения с предлагается численно-аналитическая модель, в которой выделяется два малых параметра. Благодаря этому решение расщепляется на два не сопряжённых друг с другом решения: универсальное численное и аналитическое. Такой подход позволяет получить как решение прямой, так и обратной задачи. Данная работа посвящена решению прямой задачи. Задача о распределении давления в прямоугольном элементе разработки пласта решается численно в безразмерных координатах и является не зависящей от размеров участка и перепада давлений. Решение аппроксимируется степенными функциями и в дальнейшем используется для определения массообмена между каналом и пластом. Задача течения по каналу жидкости с трассером (течения так называемой трассерной оторочки) имеет в основе закон сохранения массы индикатора и закон Дарси. Её решение выполняется методом характеристик при условии малости параметра, отражающего отношение проницаемости пласта к проницаемости канала. Результаты численно-аналитического решения сравниваются с численными результатами, ранее установленными другими авторами. Принципиальное отличие этих решений - наличие вычислительной диссипации при разностном методе решения, осуществлённом другими авторами, которая приводит к «размыву» границ трассерной оторочки.
Трассерные исследования, канал низкого фильтрационного сопротивления, задача с малыми параметрами, расщепление решения, численно-аналитическая модель, закон сохранения массы, верификация решения
Короткий адрес: https://sciup.org/143182739
IDR: 143182739 | УДК: 532.5-1/-9 | DOI: 10.7242/1999-6691/2024.17.1.2
Текст научной статьи Численно-аналитическая модель для интерпретации результатов индикаторных исследований нефтяных пластов: решение прямой задачи при наличии каналов низкого фильтрационного сопротивления
Индикаторные или трассерные подходы относятся к промыслово-геофизическим исследованиям потоков жидкости вблизи скважины и в межскважинном пространстве [1 –3] и заключаются в закачке в скважину или в размещении в её конструкции специальных меток (трассеров, индикаторов), выход которых оценивается в отбираемых пробах. Анализ динамики меток позволяет делать заключения о характеристиках потоков жидкости. Подходы различаются по типу веществ, используемых в качестве меток [4] , а также по целям исследования [5 –11] . Наибольшую историю имеют те из них, в которых определяется гидродинамическая связь нагнетательных и добывающих скважин [5 –8] .
Односкважинный трассерный тест запатентован еще в начале 1970-х годов [12] , но получил распространение лишь в последнее время, с расширением практики применения методов увеличения нефтеотдачи [13 –15] . Многочисленные публикации показывают следующие качественные и количественные результаты. Выход меток в добывающие скважины наблюдается через очень короткий интервал времени только в некоторых из них. Если считать, что распространение меток происходит по минимальному расстоянию между скважинами, то скорость их перемещения составляет от 50 до 5000 м/сут, в то время как скорость течения жидкости по пористым пластам менее 5 м/сут [16] . Аномально большая скорость движения меток (трассеров) объясняется наличием так называемых каналов низкого фильтрационного сопротивления (КНФС). Однако часть добывающих скважин не содержит в продукции меток в течение всего исследования, а следовательно, и КНФС. С другой стороны, концентрация меток в продукции реагирующих добывающих скважин показывает, что доля КНФС в притоке жидкости в скважину в большинстве случаев составляет менее 1%.
Таким образом, для интерпретации данных трассерных подходов необходим специальный алгоритм. Разработка такого алгоритма приписывается Джонсу [17] и Полларду [18] . В основе алгоритма лежит допущение, что КНФС образуют единый трещиноватый канал, изолированный от остальной части пласта. Канал связывает нагнетательную и добывающую скважины по минимальному расстоянию L, имеет поперечную площадь
Статья опубликована в открытом доступе по лицензии CC BY 4.0
S , соответственно, объём V = SL , обладает постоянной проницаемостью k f и обеспечивает идеальную гидродинамическую связь между скважинами. В рамках этого допущения за промежуток времени между началом закачки трассера и проявлением максимума его концентрации в добывающей скважине по длине канала l, вязкости воды в пластовых условиях µ w , перепаду давления между скважинами ∆p и фазовой проницаемости воды при остаточной нефтенасыщенности k r (S or ) можно аналитически рассчитать среднюю скорость движения жидкости по единому КНФС и его проницаемость (при условии, что фильтрация жидкости в нём происходит по закону Дарси). Объём вынесенного в добывающую скважину трассера позволяет определить объём КНФС. Ввиду аналогии между законом Дарси в пористой среде и законом Пуазейля для трещины единый канал можно рассматривать как трещину. До сих пор нет однозначной трактовки происхождения КНФС. Существуют теории «ручейковой» и техногенной природы, связывающие их образование с закачкой воды [16, 19] , форсированным отбором жидкости [18] , превышением забойным давлением в нагнетательной скважине критического давления трещинообразования [20] .
Традиционные алгоритмы интерпретации данных трассерных исследований не учитывают наличие нескольких КНФС и расхождение их под разными углами. Представить развитие каналов можно с помощью деформационно-гидродинамических моделей, которые учитывают связь геометрических параметров канала (или трещины) с давлением и базируются на классической системе уравнений гидродинамики. Решение уравнений осуществляется численно с помощью неявных методов, которые являются безусловно устойчивыми. Результаты расчётов по этим моделям показывают, что при большой мощности пластов (толщиной более 50 м), низкой проницаемости (менее 10 - 15 м 2 ) и низкой анизотропии поля горизонтальных напряжений (менее 1-2%) возможно изменение направления распространения трещин [9, 21] . Экспериментальные данные и более грубые оценки указывают на вероятность поворота трещин вплоть до 90 ° [19, 22, 23] . Установлено, что из системы первоначальных трещин вокруг скважины при невысоких темпах закачки жидкости наблюдается развитие одной магистральной трещины, а при больших расходах формируется частично ориентированная система трещин [24] .
Попытки моделирования КНФС за счёт слоистой неоднородности или «суперколлекторов» (пластов с очень высокой проницаемостью) не дают физически обоснованных результатов, и приходится прибегать к модели дискретной системы трещин или брать в расчёт проницаемости трубок тока с минимальной длиной между нагнетательной и добывающей скважинами [25] . Наиболее адекватный учёт перетоков жидкости между пластом и магистральной трещиной реализован в численной модели, описанной в работе [26] . Математическая модель состоит из конвективного уравнения переноса трассера с учётом источников и стоков массы (скважин), уравнения неразрывности и закона Дарси. Дополнительное условие учитывает адсорбцию трассера в пласте. Решение системы уравнений осуществляется численно на двумерной неструктурированной сетке Вороного [26] , трещина моделируется набором прямоугольных ячеек с шириной, равной её ширине. Показано, что учёт перетоков между пластом и трещиной увеличивает интерпретируемый объём канала (трещины). Однако вследствие использования численных методов итоговое решение для переноса трассера может содержать признаки диссипации, не имеющей физической природы, что является недостатком модели, приведённой в работе [26] . При численном моделировании алгоритм решения обратных задач или интерпретации параметров КНФС существенно усложняется, а наличие нескольких каналов вообще препятствует решению обратных задач, так как появляется еще один неизвестный параметр — конфигурация еще одного КНФС. С другой стороны, максимум концентрации трассера в выходящей из канала жидкости в первом пике может быть новым настроечным параметром.
Следует отметить, что традиционно считается, что метки не уходят из КНФС в пласт, поэтому концентрация индикаторного раствора формируется притоком жидкости в добывающую скважину из пласта и из КНФС. Но это упрощение расходится с практическими результатами. Поэтому цель настоящей работы состоит в создании численно-аналитической модели, учитывающей отток индикатора из КНФС в пласт. Впервые посредством метода характеристик получено аналитическое решение для распределения концентрации в КНФС, причём использование аналитических решений, в отличие от работы [26] , позволяет избежать вычислительной диссипации концентрации трассера. Кроме того, предлагается новый способ аппроксимации численного решения уравнения Лапласа для давления в виде степенных функций. В статье приводится решение прямой задачи – задачи определения концентрации трассера при его прорыве в добывающую скважину. Обратная задача – отыскание параметров КНФС, относится к планируемым исследованиям.
-
2. Суперпозиция решений задач течении жидкости в пласте и КНФС между нагнетательной и добывающей скважинами
Слабое взаимодействие трещины с пластом, отмеченное в проанализированных в разделе 1 статьях, позволяет сделать допущение о суперпозиции решений задач фильтрации в пласте и в КНФС. В качестве примера далее рассматривается пятиточечная система разработки: в центре нагнетательная скважина, в идеале работающая
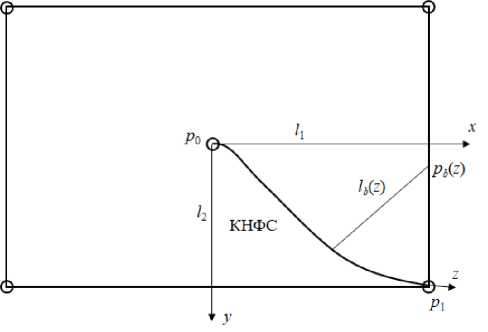
Рис. 1. Элемент пятиточечной системы разработки с КНФС; декартовы координаты x,y привязаны к геометрии участка, вспомогательная ось z -– к направлению течения и форме канала на четыре добывающих скважины, но эти скважины в свою очередь связаны с другими нагнетательными скважинами. Дебит добывающих скважин равен четверти расхода нагнетательной скважины. Три четверти дебита поступают от нагнетательных скважин, находящихся вне выбранного участка (Рис. 1). Пласт считается однородным по проницаемости, жидкость и скелет пористой среды — несжимаемыми. Для того чтобы адекватно смоделировать эту систему разработки, необходимо рассмотреть работу всего участка, в общем случае — прямоугольного. Так как конфигурация КНФС не известна, то считается, что канал имеет длину l и направлен от нагнетательной скважины к добывающим скважинам (Рис. 1). Вводятся декартовы координаты x, y и вспомогательная ось z; выделяется расчётная область с полудлинами сторон l1 и l2 .
Поля давления и потоков однородной жидкости в пласте при отсутствии КНФС определяются из решения уравнения Лапласа [26] . В силу симметрии выделенной области (с одной нагнетательной и одной добывающей скважиной) её границы считаются линиями непротекания флюида. Так как соотношение расходов жидкости, закачиваемой в пласт и находящейся в КНФС неизвестно, то на скважинах выставляются постоянные значения давлений:
-
d 2 p / dx 2 +d 2 p / dy 2 = 0 ,
x = 0, y = 0: p=po, x = 11, У = I2 : P=Pi, (1)
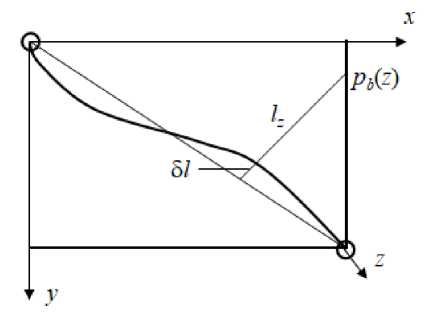
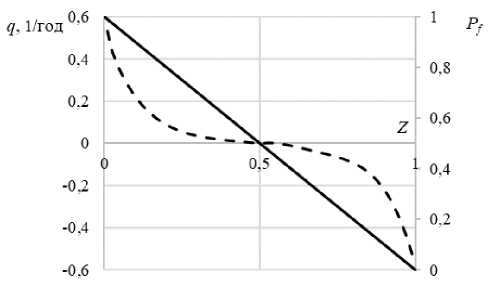
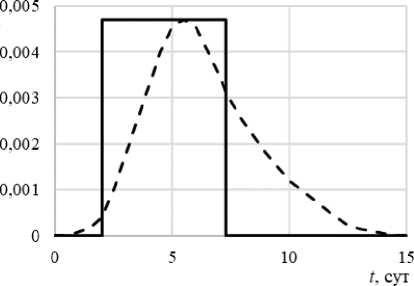
0 Введение безразмерных переменных позволяет отыскать общее решение для различных как геометрии участка, так и давлений на скважинах, которое далее будет называться универсальным: X = x/li, Y = y/l2, P =(p-pi)/(po —pi). (2) В случае квадратного участка фиксированные безразмерные давления на скважинах равняются P (0,0) = 1, P (1,1) = 0. Поиск аналитического решения задачи (1) осложнён разрывными граничными условиями, поскольку скважины располагаются не по всей границе расчётной области, а только в определённых точках. Поэтому задача (1) решается численно. Её решение в безразмерных переменных (2) получено на основе схемы «крест» с помощью метода простой итерации [27] на сетке 100 х 100 ячеек. В центральном узле располагалась нагнетательная скважина, в угловых — добывающие. Количество узлов для построения разностной схемы бралось таким, при котором результаты решения задачи (1) отличались от результатов решения на сетке с превышающим в 4 раза количеством узлов не более, чем на 5%. Результат универсального численного решения P(X,Y) на квадратной сетке представлен на рисунке 2. Чем темнее серый цвет, тем меньше значение давления. Видно, что вблизи скважин давление изменяется практически по логарифмическому закону. Вблизи нагнетательной скважины в пласте наблюдается повышение давления, вблизи добывающей — снижение, в остальной части пласта давление остаётся почти невозмущённым. Давление в КНФС подчиняется закону сохранения массы жидкости с учётом перетоков в пласт. При использовании закона Дарси для описания фильтрации жидкости в случае стационарного процесса выражение баланса массы в выбранной точке КНФС принимает вид: kf d2pf µw dz2 где pf — давление в КНФС, qi — перетоки жидкости через левую (i = 1) и правую (i = 2) боковые поверхности канала (см. Рис. 3), kf — эффективная проницаемость КНФС, µw — динамическая вязкость воды в пластовых условиях. В общем случае перетоки жидкости из канала и обратно будут различными и при прямоугольной форме расчётной области. Если рассматривать единый КНФС как систему магистральных поровых каналов, то для связи пористости m и проницаемости единого канала, согласно теории Козени–Кармана [28], можно использовать экспериментальную зависимость k (m), характерную для кернов конкретного месторождения. В качестве величины пористости канала будет выступать значение максимальной пористости для наиболее плотной упаковки шариков одинакового радиуса m = 0,476. В рамках концепции об автогидроразрыве пласта как природе трещин (КНФС) эффективная проницаемость трещины определяется её шириной w: kf = w2/12. Следовательно, только один фильтрационноёмкостный параметр канала является независимым. В исследовании, которому посвящена настоящая статья, таковым считается w. С учётом этого принято, что высота трещины (канала) совпадает с продуктивной мощностью пласта. Таким образом, введенные величины есть функции поперечной толщины КНФС: kf (w), m(w). Полагается, что КНФС не влияет на параметры, входящие в уравнения (1), в самых удалённых точках расчётной области. Давление pb (x,y) на границах расчётной области, удалённых от канала, можно аппроксимировать подходящей аналитической функцией. Каждой точке единого КНФС соответствует граничное значение давления pb (z) и расстояние до границы lb (z) (см. Рис. 1). Так как каналы формируются около диагонали выделенного элемента участка разработки, то принимается, что расстояние от канала до границы lb (z) определяется перпендикуляром lz от границ участка к выделенной на его диагонали точке (Рис. 3). Если считать перетоки между КНФС и пластом установившимися, то они опишутся одномерным законом Дарси: qi = kkr (Sor ) (pf -Pb(x,y)) µl lb (i = 1,2), где k — абсолютная проницаемость пласта, kr(Sor) — фазовая проницаемость воды при остаточной нефтенасыщенности, µ — усредненная вязкость пластового флюида, i — индекс, указывающий на номер боковой поверхности КНФС. Суммарный приток из пласта в произвольную точку канала, согласно (3) и (4), с точностью до величины δl2lz2аппроксимируется упрощённой формулой: -(qi+q2) 2kkr(Sor) (pf-pb(x,y)) µl lz где lb= lz— 81 (см. Рис. 3). После введения безразмерных координат и переменных Z z l, Lb(Z)= , lz , P2+2 pf -p1 Pf =------, p0 -p1 Pb(Z ) = pb(z) -pi p0 -p1 Рис. 2. Расчётное распределение давления в выделенной области пласта; чёрные линии показывают значения, полученные с использованием степенных функций Рис. 3. Пояснение к определению перетоков жидкости между КНФС и пластом уравнение (3) с учётом (5) и (6) принимает вид: d2Pf dZ2 (Pf-Pb(Z)) FZ (Pf-Pb(Z)) F 1 -Z Z< 0,5, Z > 0,5, где F = 2kkr(Sor)/kf — безразмерный критерий подобия. По оценкам [26] он имеет порядок 10-3-10-5, что говорит о пренебрежимо малых перетоках между КНФС и пластом и о возможности аппроксимации с высокой точностью распределения давления линейной функцией с пределами 1 и 0. Прямое использование результатов численного решения не позволяет при дальнейших расчётах получить полуаналитические решения. Поэтому далее зависимость давления на границах области от безразмерной координаты Z для универсального решения представляется степенными функциями: 0 < Z< 0,5: Pb(Z ) = 12,75^(1 -2Z )2+ 1)5/2-41,39((1-2Z)2 + 1)2 +42,11^(1 -2Z )2+ 1)3/2- -10,82^(1-2Z )2+ 1)-2,15((1 -2Z )2+ 1)1/2, (8) 0,5 -90,24(1-Z )2+ 10,56(1-Z), с погрешностью до 10% (Рис. 2, сплошные чёрные линии). Выбор для аппроксимации степенных функций обусловлен удобством их последующего интегрирования. Старшая степень и коэффициенты в слагаемых выражения (8) таковы, что позволяют достигать заданной погрешности решения. Рис. 4. Распределение давления жидкости в пласте (сплошная линия) и её перетоков из КНФС (штриховая линия) в зависимости от обезразмеренной длины канала На рисунке 4 приведены результаты расчёта перетоков из КНФС в зависимости от координаты Z , где q обозначает суммарный переток. Расчёты показывают, что в первой части канала — части, ближней к нагнетательной скважине, наблюдается переток жидкости в пласт (расход в выражении (4) положителен), а во второй части, наоборот, жидкость поступает в КНФС (расход в выражении (4) отрицателен). Этого можно было ожидать, так как характер распределения давления вблизи скважины близок к логарифмическому, а в канале он линейный. Это различие имеет место как вблизи добывающей, так и рядом с нагнетательной скважиной, но уже с обратным знаком. Таким образом, в данном разделе найдено распределение давления в пласте и в КНФС. Эти расчёты необходимы для решения задачи о движении оторочки индикатора в КНФС. 3. Решение задачи о движении оторочки трассера в КНФС Далее рассматривается задача о движении флюида с закачанным в пласт индикаторным (трассерным) раствором, при этом диссипация концентрации трассера не учитывается. В этом случае сохраняются интегральные характеристики оторочки трассера, приходящей в добывающую скважину (масса вещества, выполняющего роль трассера). Анализ работ по индикаторным исследованиям [29, 30] позволил установить, что в некоторых случаях коэффициент диссипации концентрации не превышает значения 10-7м2/с. В качестве трассеров выбираются вещества с минимальной адсорбцией в пористой среде, поэтому в данной работе диссипация концентрации меток игнорируется. Расщепление исходной задачи на задачи фильтрации жидкости в пласте и КНФС позволяет найти важное соотношение между долей жидкости, закачиваемой в пласт, и долей её поступления в единый канал. Объём жидкости, подаваемой в пласт — Q, определяется путём универсального численного решения уравнения (1), объём жидкости, поступающей в КНФС — Qf , рассчитывается с учётом линейного распределения давления в канале. Формулы, по которым вычисляются потоки жидкости в пласт и канал, имеют вид: 2kkr(Sor)h(po-pi) /2I2AY(1-Pox) 2liAX(1-Poy) M \ 11AX +l2AY kfA Qf ,'P'-' —Pi), µwl где P0X и P0Y — расчётные безразмерные давления в ячейках, по направлению осей X и Y соседних с центральной, h — эффективная мощность пласта, ∆X, ∆Y — размеры расчётных ячеек в универсальном решении, A — площадь поперечного сечения канала, которая обуславливается принятой геометрией канала (при геометрии канала в виде эллипса для случая h > w она равна A = nhw/4). Благодаря несопряжённости задач, решаемых вместо исходной задачи, скорость движения оторочки является постоянной величиной и определяется выражением (9). Тогда уравнение сохранения в КНФС массы индикатора при пренебрежении его диффузией в размерных переменных имеет вид: ∂c Qf ∂c mdt+Tsz = | qc, q>О, q(i-c), q<0, где c — концентрация трассера в водной фазе, q — перетоки жидкости в пласт (рассматривается квадратная геометрия участка, поэтому q1 = q2 = q/2), определяемые законом Дарси (4); в (10) учитывается, что отток жидкости из КНФС приводит к потере трассера, а приток из пласта — к снижению его концентрации пластовым флюидом. Введение безразмерных времени и концентрации T = Qf t/(Aml), C = c/c0 приводит уравнение (10) к виду: ∂C ∂C dT + dZ FC fl— PW , Z< 0,5, 1-Z F (“ — C )(1 — Pb^Zz \ Z> 0,5, c0 1 - Z где c0 — концентрация трассера в водной фазе при закачке. Уравнение переноса трассера содержит уже два малых параметра: c0 и F — безразмерный критерий подобия, введённый в разделе 2. Концентрация трассера определяется специальным подбором веществ–индикаторов и, как правило, мала: с0 ~ 10 2 — 10 3. Линеаризация уравнения (пренебрежение членами порядка cF) даёт упрощённое линейное уравнение: ∂C ∂C дт+dZ Z< 0,5, Л Pb(z)А 1 — Z ’ Z> 0,5, где член F/с0, отвечающий за разбавление оторочки трассера при перетоке воды в трещину (канал), имеет порядок единицы. Таким образом, потери трассера за счёт оттока содержащего его раствора в пласт, наблюдаемые в первой части канала, пренебрежимо малы, а снижение концентрации трассера происходит во второй части канала НФС, где приток пластовой воды в канал приводит к разбавлению индикаторного раствора. Далее, для гиперболического уравнения (12) формулируется задача Коши при следующих ограничениях: T = 0, Z> 0 : C (Z) = 0; 0 dZ dC dT = : dZ 0, Z < 0,5, F Л - Pb(Z) А со 1-Z ’ Z> 0,5. Характеристическая скорость определяет время (T = 1), за которое жидкость, имеющая концентрацию трассера (13), достигает добывающей скважины (Z =1). Но необходимо помнить, что добывающая скважина работает с дебитом, который создают четыре ближайшие нагнетательные скважины. Поэтому реальная концентрация трассера в добывающей скважине будет в четыре раза меньше. Если известна концентрация приходящего индикаторного раствора, то расчёт общей массы приходящего по данному каналу вещества, играющего роль трассера, не составляет труда (наклон всех характеристик одинаковый). Из зависимости давления (8) в случае универсального решения можно вычислить значение концентрации трассера, приходящего в конкретную добывающую скважину, с учётом работы окружающих добывающих скважин. Это решение имеет вид: F C * =0,25 1— . c0 Рис. 5. К сравнению динамики концентрации трассера в добывающей скважине: численноаналитическая модель (сплошная линия), модель из [26] (штриховая линия) Для проверки адекватности сделанных допущений рассчитан пример закачки оторочки трассера из работы [26]. Сравнить полученные данные о динамике концентрации трассера в добывающей скважине с данными численного решения из указанной работы можно на рисунке 5. Следует отметить, что оба расчёта правильно воспроизводят массовый баланс трассера и время подхода оторочки к добывающей скважине. Однако в работе [26], как и в осуществлённом числено-аналитическом решении, диффузия трассера и диссипация его концентрации отсутствуют, что позволяет сделать вывод о том, что причиной «размыва» оторочки трассера в канале является вычислительная диссипация, которая определяется особенностями выбранной численной схемы. В аналитическом решении оторочка движется по каналу, претерпевая снижение концентрации трассера за счёт притока воды в канал, но без «размыва» фронтов оторочки. При решении обратных задач интерпретации промысловых исследований учёт вычислительной диссипации становится особенно важным. 4. Выводы Таким образом, из анализа решения на основе разработанной численно-аналитической модели прямой задачи — задачи определения концентрации трассера при его прорыве в добывающую скважину, сделаны следующие выводы: 1. Предлагаемая численно-аналитическая модель расчёта параметров трассерных исследований в КНФС позволяет выделить два малых параметра — отношение проницаемости пласта к проницаемости канала и исходную концентрацию трассера, определяющих происходящие процессы. 2. Модель даёт возможность расщепить исходную задачу на две: задачу отыскания давления в породе участка разработки и в КНФС. С использованием численных методов выполнено универсальное решение уравнения Лапласа для распределения давления на прямоугольном участке пласта с нагнетательной скважиной в центре (источник) и четырех добывающих по углам (стоки). Так как решение получено в безразмерных координатах, то его можно применять как при любых значениях перепада давлений между нагнетательной и добывающими скважинами, так и размерах участка. 3. Установлено, что перетоки трассера из КНФС малы, а его концентрация в канале снижается за счёт разбавления водой, поступающей из пласта. Показано, что перетоки жидкости между пластом и каналом практически не влияют на распределение давления в пласте и канале. 4. Представлен пример расчёта движения оторочки трассера по каналу с выходом меток в добывающую скважину. Результаты вычислений по предложенной численно-аналитической модели удовлетворительно согласуются с результатами численного решения сопряжённой задачи из [26]. Продемонстрировано, что обнаруженный в [26] «размыв» фронтов оторочки происходит за счёт вычислительной диссипации.
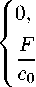
Список литературы Численно-аналитическая модель для интерпретации результатов индикаторных исследований нефтяных пластов: решение прямой задачи при наличии каналов низкого фильтрационного сопротивления
- Сафаров Ф.Э., Вежнин С.А., Вульфович С.Л., Исмагилов О.З., Малыхин В.И., Исаев А.А., Тахаутдинов Р.Ш., Телин А.Г. Трассерные исследования и работы по выравниванию профиля приемистости в скважине Дачного месторождения // Нефтяное хозяйство. 2020. № 4. C. 38–43. DOI: 10.24887/0028-2448-2020-4-38-43.
- Манасян А.Э., Журавлев Д.А., Козлов А.Н. Опыт применения трассерных исследований пласта ДIII Западно- Коммунарского месторождения // Нефтепромысловое дело. 2018. № 9. C. 41–47. DOI: 10 . 30713 / 0207 - 2351 - 2018-9-41-47.
- Дягилев В.Ф., Кононенко А.А., Леонтьев С.А. Анализ результатов трассерных исследований на примере пластов ЮВ11 Чистинского месторождения // Успехи современного естествознания. 2018. № 1. C. 93–101.
- Соколовский Э.В., Соловьев Г.Б., Тренчиков Ю.И. Индикаторные методы изучения нефтеносных пластов. M.: Недра, 1986. 157 с.
- Конев Д.А. Исследование нефтяных пластов с помощью индикаторного метода // Современные наукоемкие технологии. 2014. № 7–2. C. 23–26.
- Beier R.A., Sheely C.Q. Tracer Surveys To Identify Channels for Remedial Work Prior to CO2 Injection at MCA Unit, New Mexico // Society of Petroleum Engineers and US Department of Energy Enhanced Oil Recovery Symposium, Tulsa, USA, 17–20 April 1988. 1988. SPE-17371-MS. DOI: 10.2118/17371-MS.
- Lichtenberger G.J. Field Applications of Interwell Tracers for Reservoir Characterization of Enhanced Oil Recovery Pilot Areas // Production Operations Symposium, Oklahoma City, USA, 7–9 April 1991. 1991. SPE-21652-MS. DOI: 10.2118/21652-MS.
- Zecheru M., Goran N. The use of chemical tracers to water injection processes applied on Romanian reservoirs // EPJ Web of Conferences. 2013. Vol. 50. 02005. DOI: 10.1051/epjconf/20135002005.
- Павлов И.В., Мозговой Г.С. Трассерные методы идентификации и мониторинга притока флюидов в добывающие скважины // Нефть, газ. Новации. 2020. № 1. C. 63–66.
- Гурьянов А., Каташов А., Овчинников К. Диагностика и мониторинг притоков скважин с помощью трассеров на квантовых точках // Время колтюбинга. Время ГРП. 2017. № 2. C. 42–51.
- Овчинников К.Н., Котенёв Ю.А., Султанов Ш.Х., Чибисов А.В., Чудинова Д.Ю. Регулирование процесса выработки запасов углеводородов на основе динамического трассерного мониторинга профиля притока горизонтальных скважин // Георесурсы. 2022. Т. 24, № 4. C. 126–137. DOI: 10.18599/grs.2022.4.11.
- Deans H. Method of determining fluid saturation in reservoirs. 1971. US Patent № 3623842.
- AlAbbad M.A., Sanni M.L., Kokal S., Krivokapic A., Dye C., Dugstad Ø., Hartvig S.K., Huseby O.K. A Step Change for Single-Well Chemical-Tracer Tests: Field Pilot Testing of New Sets of Novel Tracers // SPE Reservoir Evaluation & Engineering. 2018. Vol. 22, no. 1. P. 253–265. DOI: 10.2118/181408-PA.
- Mechergui A., Agenet N., Romero C., Nguyen M., Batias J. Design, Operation, and Laboratory Work for Single-Well Tracer Test Campaign in Handil Field Indonesia // SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 2–4 July 2013. 2013. SPE-165227. DOI: 10.2118/165227-MS.
- Мухутдинова А.Р., Болотов А.В., Аникин О.В., Варфоломеев М.А. Алгоритм оценки рабочего интервала распределяющегося трассера для применения в односкважинном трассерном тесте // Георесурсы. 2022. Т. 24, № 4. C. 75–81. DOI: 10.18599/grs.2022.4.6.
- Тарасов М.Г., Волков В.Н., Сианисян Э.С., Трунов Н.М. Формирование техногенных гидрогеодинамических систем при эксплуатации нефтяных месторождений // Георесурсы, геоэнергетика, геополитика. 2015. Вып. 12, № 2. 9. DOI: 10.29222/ipng.2078-5712.2015-12.art9.
- Викторин В.Д. Влияние особенностей карбонатных коллекторов на эффективность разработки нефтяных залежей. M.: Недра, 1988. 149 с.
- Хисамов Р.С., Файзуллин И.Н., Кубарев П.Н., Антонов Г.П., Галимов И.Ф. Результаты исследований фильтрационных свойств трещиноватых коллекторов 303 залежи, разрабатываемой на естественном водонапорном режиме // Нефтяное хозяйство. 2011. № 7. C. 36–39.
- Изотов А.А., Соколов С.В. Целесообразность плавного запуска в работу нагнетательных скважин // Экспозиция Нефть Газ. 2021. № 1. C. 40–44. DOI: 10.24412/2076-6785-2021-1-40-44.
- Изотов А.А., Афонин Д.Г. О техногенной трансформации продуктивных пластов вследствие повышенного давления нагнетания при заводнении // Нефтепромысловое дело. 2021. № 5. C. 18–25. DOI: 10.33285/0207-2351-2021-5(629)- 18-25.
- Павлов В., Корельских Е., Бутула К., Клюбин А., Максимов Д., Зиновьев А., Задворнов Д., Грачев О. Создание 4Д геомеханической модели для определения влияния разработки месторождения на геометрию трещин ГРП // Российская нефтегазовая техническая конференция и выставка SPE, Москва, Россия, 24–26 октября 2016. 2016. SPE-182020-RU. DOI: 10.2118/182020-RU.
- Асалхузина Г.Ф., Давлетбаев А.Я., Федоров А.И., Юлдашев А.Р., Ефремов А.Н., Сергейчев А.В., Ишкин Д.З. Диагностирование переориентации техногенной трещины при повторном гидроразрыве пласта методами анализа добычи/давления и моделирования в геомеханическом симуляторе // Российская нефтегазовая техническая конференция SPE, Москва, Россия, 16–18 октября 2017. 2017. SPE-187750-RU. DOI: 10.2118/187750-RU.
- Kuzmina S., Butula K.K., Nikitin A. Reservoir Pressure Depletion and Water Flooding Influencing Hydraulic Fracture Orientation in Low-Permeability Oilfields // SPE European Formation Damage Conference, Scheveningen, The Netherlands, 27–29 May 2009. 2009. SPE-120749 DOI: 10.2118/120749-MS.
- Zazovsky A.F. Propellant fracturing revisited // Proceedings of the 6th North America Rock Mechanics Symposium, Gulf Rocks, USA, 5–9 June 2004. 2004. ARMA/NARMS 04-612.
- Булыгин Д.В., Николаев А.Н., Елесин А.В. Гидродинамическая оценка эффективности потокоотклоняющих технологий в условиях образования техногенных каналов фильтрации // Георесурсы. 2018. Т. 20, № 3. C. 172–177. DOI: 10.18599/ grs.2018.3.172-177.
- Киреев Т., Булгакова Г.Т. Интерпретация трассерных исследований с помощью дискретной модели трещины // Вычислительная механика сплошных сред. 2018. Т. 11, № 3. C. 252–262. DOI: 10.7242/1999-6691/2018.11.3.19.
- Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. 432 с.
- Баренблатт Г.И., Ентов В.М., Рыжик В.М. Движение жидкостей и газов в природных пластах. M.: Недра, 1984. 211 с.
- Anisimov L.A., Kilyakov V.N., Vorontsova I.V. The Use of Tracers for Reservoir Characterization // SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15–18 March 2009. 2009. SPE-118862 DOI: 10.2118/118862-MS.
- Eldaoushy A.S., Al-Ajmi M., Ashkanani F. Utilization of Interwell Water Tracer to Study Subsurface Flow of the Injected Water and Optimize Waterflood in Mauddud Carbonate Reservoir, Raudhatain Field, North Kuwait // SPE Kuwait Oil and Gas Show and Conference, Mishref, Kuwait, 11–14 October 2015. 2015. SPE-175200-MS DOI: 10.2118/175200-MS.


