Численное исследование генерации волн на поверхности при погружении твёрдого тела в жидкость

Особый интерес в последнее время вызывает возможность возникновения катастрофических волн цунами при падении в океан тел из межпланетного пространства. Такие волны в современной научной литературе принято называть космогенными цунами [1]. Падение метеорита в океан может привести к появлению цунами колоссальной высоты, а если учесть, что поверхность океана занимает значительную площадь земной поверхности, то падение метеорита в океан более вероятно, чем на сушу. Хотя сценарий падения метеорита с необходимыми для возбуждения достаточно крупной волны размерами маловероятен, всё же проблема прогнозирования такого явления остаётся [1].

Задача возникновения космогенных цунами включает в себя различные проблемы гидроаэродинамики, механики твёрдого тела, динамики многокомпонентных сред, теории вероятности и других, поэтому из-за высокой совокупной сложности она разделяется на ряд подзадач, в каждой из которых делаются определённые допущения.

Проблеме цунами, вызванных падением «внеземных» объектов в океан, посвящён ряд работ. В некоторых, в частности, проводится анализ статистических данных известных явлений, относящихся к космогенным цунами. Например, в работе [2] с помощью простых аналитических выкладок описывается процесс образования цунами.

Падение или погружение «внеземного» тела здесь не рассматривается, а задаётся начальная деформация водной поверхности в виде каверны, которая, следуя статистическим данным, отражает падение астероида в океан. В [2] также предлагаются вероятностные оценки и эмпирическая формула понижения амплитуды волны, основанная на аналитических выкладках авторов.

Интересный численный расчёт приводится в работе [3], где рассматривается падение астероида, а точнее, твёрдого тела заданного размера. Для расчёта образования возмущения водного слоя используется довольно сложная численная схема, а для образования цунами — другая схема, в которой применяются данные, полученные с помощью первой. Подобное сопряжение вычислений как трудоёмко, так и малодостоверно. Работа [3] в большей мере относится к задаче падения астероида в общем, а не к моделированию цунами как возможного последствия такого явления.

Современный обзор исследований, касающихся падения астероидов в океан, содержит монография [1]. Также в ней даётся аналитическое представление образования цунами при распаде на водной поверхности заданной каверны; проводятся расчёты на основе потенциальной модели движения жидкости; приводятся количественные оценки явления и вероятностные данные по проблеме.

В настоящей работе рассматривается полный расчёт образования поверхностных волн, возникших при погружении твёрдого тела в жидкость, то есть учитывается как само волнообразование, так и зависимость параметров сгенерированных волн от параметров тела. Твёрдое тело представляет собой цилиндр с круговым сечением, «головная» часть которого в одном случае имеет плоское затупление, а в другом — полусферическое. Возникшие волны обладают нелинейным характером, и для их адекватного описания необходимо привлекать нелинейные модели волновой гидродинамики. В данной работе используется модель движения жидкости на основе уравнений мелкой воды, записанных в цилиндрической системе координат. Конечноразностный аналог исходной системы дифференциальных уравнений строится с помощью разностной сетки типа «C» по классификации Аракавы. Численное решение находится с использованием явной TVD схемы первого порядка точности по пространству и времени [4, 5].

При погружении в жидкость цилиндр ведёт себя как поршень и, вытесняя жидкость, испытывает сопротивление, теряет скорость. У стенки цилиндра уровень жидкости повышается и, достигнув определённого значения, образует волну. После того как цилиндр прекращает движение, образованная волна отходит от его стенки. С течением времени амплитуда волны убывает. В работе выявлены зависимости амплитуды образованных волн от параметров погружающегося тела: его начальной скорости и размеров.

• 2.    Постановка задачи

Рассматриваем осесимметричное течение идеальной несжимаемой жидкости, ограниченной снизу дном Γ ₀ , заданным функцией z = - b ≡- 1 , и осью симметрии Γ ₁ с абсциссой r = 0 . Здесь r , z — координаты точек в цилиндрической системе координат Orz , имеющей горизонтальную ось Or , лежащую на невозмущённой свободной поверхности жидкости, и вертикальную ось Oz (Рис. 1). Цилиндр задаём как непроницаемую поверхность Γ ₂ , которая зависит от формы «головной» части и описывается следующим образом: – при полусферическом затуплении

S 1 ( r , t ) = R b - R b ² - r ² - V b ( t ) ⋅ t ,    0 ≤ r ≤ R b ,

– при плоском торце

S 2 ( r , t ) = - V b ( t ) • t ,     0 <  r <  R b .

Здесь R_b — радиус цилиндра, V_b ( t ) — скорость его погружения.

Свободная поверхность жидкости Г _f подлежит определению. Будем считать, что она описывается однозначной функцией z = n ( r , t ), где t — время. Введём безразмерные величины по формулам:

r

r

H 0 ^,

~b ~ g          u b =----, t = t ----, u = ,       ,

H 0            H 0         gH 0

где g = const — ускорение свободного падения, H0 — характерная глубина (глубина в начальный момент времени), u — скорость движения жидкости. Символ «~», которым отмечены безразмерные величины, при последующем изложении опускается.

При введённом обезразмеривании критериями подобия являются: X = H ₀ [R_b , число Фруда F = V_o /gH 0 ⁽ V b ,0 — начальная скорость тела), а также отношение плотности жидкости к плотности тела: R = р l /р _b .

При погружении в жидкость тело испытывает сопротивление. Закон движения, которому оно подчиняется, записывается как

MV_b =-р/ CVS bld ₂

[6] (силой тяжести

пренебрегаем), где M = 4рbпRb,3 — масса погружающегося тела, S = пR2 — площадь миделевого сечения, Cd = 1 — коэффициент сопротивления [7]. Это уравнение имеет простое решение: Vb = Vb0 • eаL, в котором L — путь тела (в данном случае это —

3    Cр глубина водного слоя) и а =---d—l-. Если в решение подставить «реалистичные»

• 8    R b Р ь

значения, например, глубину водного слоя 1 километр и радиус тела 10 метров, начальную скорость и плотность тела, соответственно, 25 км/с и 3 •Ю3 кг/м3, то видно, что скорость тела быстро падает: от начального значения до почти нулевого — 0,09 м/с. Следовательно, сопротивлением пренебрегать нельзя; поэтому ищем также и решение системы (обезразмеренной):

3 _

V b =-- C d XRVb,    z b = V b ( t ).

Для моделирования течения жидкости используем одномерные уравнения мелкой воды в цилиндрической системе координат:

Hu

П t ^{+ (} Hu ) r = --,

r

<

( Hu ), + Hu ² +---

‘ I 2 J r

Hu ²

,

r

H = n + b.

Решение задачи, заключающееся в определении изменения уровня поверхности жидкости и зависимости максимальной амплитуды образованных волн от параметров погружающегося тела (начальной скорости и радиуса цилиндра), состоит из решения систем (1) и (2) в соответствии с начальными и граничными условиями:

• -    в начальный момент времени t = 0 жидкость покоится ( u ( r ,0) = 0) и ограничена сверху невозмущённой свободной поверхностью ( р ( r ,0) = 0); тело имеет начальную скорость V b (0) = V_b0 и расположено над поверхностью невозмущённой жидкости так, что min S i ( r ,0) = 0; r

• -    на оси симметрии Г 1 ставится условие:

и (0, t ) = 0,       t >  0;

- на движущейся поверхности Г 2 задаётся условие непротекания:

П = S,

д ( rHu ) = д S i д r         д t

где индекс i принимает значения 1 или 2 и определяет форму затупления «головной» части цилиндра.

• 3.    Алгоритм расчёта

Численные расчёты проводились для жидкости, заполняющей бассейн с радиусом R = 0,5, причём счёт прекращался, как только образованная волна доходила до координаты r = R . Отрезок Q = [ 0; R ] равномерно, с постоянным шагом h , покрывался интервалами Q h ; общее количество ячеек в направлении оси Or составляло N . Согласно сетке типа «С» по классификации Аракавы [4] на границах каждого Q _h вычислялись значения скорости u_i ⁿ и потока массы ( Hu ) _i ⁿ , а внутри интервалов — положение свободной поверхности р П^^ .

Для получения численного решения использовалась явная разностная схема с уменьшающейся полной вариацией (TVD схема) первого порядка точности по пространству и времени, описанная в работе [5]. Там же даётся условие, при котором полная вариация не увеличивается, то есть условие того, что схема обладает свойством TVD. Причём для явной схемы это условие совпадает с условием устойчивости Куранта– Фридрихса-Леви: C -A t / A r <  1 ( C — характерная скорость). Таким образом, условие КФЛ обеспечивало устойчивость выбранной разностной схемы и гарантировало отсутствие нефизических осцилляций в решении. На каждом временном слое шаг по времени определялся исходя из этого условия.

Рассмотрим алгоритм численного расчёта. Пусть на n -м слое по времени известны значения ( Ни ) П , р П₊^ . По ним вычисляем дополнительные значения: Н"^ ) =П П+yi) + b и u i = ² ( Hu ) " /( ^Н ’(„2 ) + ^Н Й1Й ) ) .

Получение решения на (n +1) -м слое состоит из нескольких этапов. На первом этапе находим шаг по времени согласно формуле т n =0 h

2max. Hn+ max un\ i V 1+(12)         /1'1

- i

где 0 = 0,1 — коэффициент устойчивости. Затем методом Эйлера ищем решение системы (1) с известным шагом по времени. Так определяем положение цилиндра на новом временном слое.

На следующем этапе, согласно работе [5], рассчитываем численные скорости переноса для уравнений переноса из системы (2):

n a / + i

= *

0,5 [ ( Hu ) " + i - ( Hu ) П - i ]

^П / + ( 12 )    ^П / - ( 12 )

n i+1,

nn

'*/+(12)    П/-(12) ^ 0, nn

¹ * / + ( 12 )     ¹ * / - ( 12 )      0;

u , '+ 1 ( Hu ) " + , + ^0,125 ( + 1,2) + + 1,2) ) - u n ( Hu ) n -

n

- + ( 12 ) =

-o-125 (++,+H'm)2 ]/((Hu) '+1)-(Hu) n),

( Hu ) - ( Hu ) ,n + 0,

n

+ 1 ,

(Hu )"„-( Hu) n = 0.

Далее, на  (n +1) -м временном слое вычисляем значение свободной поверхности n,n+11/2)

п n   -nn

¹ * / + ( 12 )       ¹ * / + ( 12 )

n h [(Hu ),., -(Hu),+ q (a+1 )(nn,(+2)

n   nnn

П + ( 12 ) ) ^- Q ^{( а )}( ^П , + ( 12 ) ^-П , - ( 12 )

-

тn 0,5((Hu)n+1 +(Hu)n)

^Г + ( 12 )

и значение потока массы ( Hu ) n ^{+ 1}

n ₂

(Hu), =(Hu), --{0,25[(Hu),., +(Hu), ](u’,1 + un) + 0,5(H/^) -

-

■0,25 (Hu)n +(Hu)n-1

( u n + u - 1 ) - ^0,5 ( H -_(V2 ) )⁵ + Q ( 1 +_{I V}2 ) ) [ ( Hu ) n + 1 - ( Hu ) ,’

- Q (l’(12))[( Hu ) n-( Hu ) n-1 ]}- +

( Hu ) n • u n

^{0,5 (} ^ + ( 12 ) ⁺ r - ( 12 ) )

-

Приведённые формулы являются разностной аппроксимацией дифференциальной системы (2), причём слагаемые, содержащие Q ( x ), представляют собой схемную численную вязкость. Множитель Q ( x ) имеет следующий вид:

0,5 ( x 75 + 5 ), | x | <5 , ^{v 7}          где коэффициент 5 = 0,125 .

Q ⁽ x ) = *

Полученные на ( n + 1) -м временном слое значения корректируем так, чтобы они удовлетворяли граничным условиям. Согласно [8], условие полного отражения для сеток типа «C» по классификации Аракавы имеют следующий вид (для левой и правой границ расчётной области):

n + 1           n + 1

u 0   = — u 2 ,

u

n + 1

N

u N — 2 ,

„ n + 1                  n + 1         n + 1

u1 = 0,     П(1/2) = П(3/2) , n+1                 n +1            n+1

u N — 1 = 0,     ^П N — ( 1/2 ) = Л N — ( 3/2 ) ^.

Поскольку задача осесимметричная, то численное представление граничного условия (3) имеет простой вид, то есть nn+1 = ZK,   (Hu )n+1 = 0,   (Hu) n+1 = М *72 (i = 17Nb), где Nb — это наибольшее количество Qh, в которых выполняется условие nn+1 ^ zn+ •

Описанные этапы численного интегрирования проводим на каждом временном слое. Во времени процесс вычислений продолжаем до тех пор, пока не будет достигнут временной слой, соответствующий требуемому расчётному времени.

• 4.    Результаты вычислительных экспериментов

Рассмотрим процесс волнообразования на примере погружения цилиндра с полусферическим затуплением в невозмущённую жидкость. При вычислениях в уравнениях (1) полагаем значение R = 1/3, которое может соответствовать плотности жидкости р l = 10 3 кг/м³ и плотности тела р _b = 3 - 10 3 кг/м³ (известная величина для каменного астероида). Картина данного процесса показана на рисунках 1 и 2, на которых изображены графики волнообразования в различные моменты времени при значениях модельных параметров: R_b = 0,1 и V_{b 0} = 30. Рисунок 2 — это увеличенная область рисунка 1, на котором видно, как цилиндр касается поверхности жидкости и как вытесняемая им жидкость движется вдоль его полусферической части и

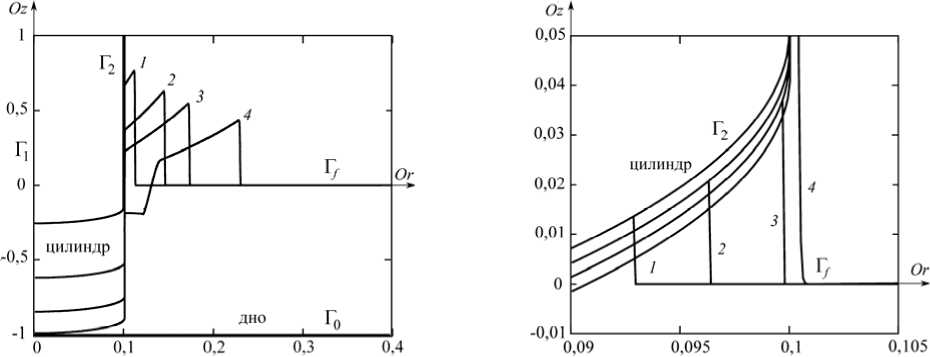
Рис. 2. Фрагмент рисунка 1. Профили свободной поверхности и цилиндра в моменты времени: 1,73 - 10 — ³ (кривая 1 );

1,83 - 10 ^{— 3} ( 2 ); 1,94 - 10 ^{— 3}( 3 ); 2,04 - 10 ^{— 3}( 4 ).

Рис. 1. Погружение цилиндра с полусферическим затуплением. Профили свободной поверхности и цилиндра в моменты времени: 1,0 - 10 — ² (кривая 1 );

3,11 - 10 ^{— 2} ( 2 ); 5,02 - 10 ^{— 2}( 3 ); 9,13 - 10 ^{— 2}( 4 ).

выходит за границу радиуса цилиндра. Погружение цилиндра сопровождается образованием возле его стенки повышения уровня жидкости (Рис. 1), которое затем распадается на волну. Уровень свободной поверхности между цилиндром и волной постепенно понижается, поверхность принимает изначальное положение. В результате формируется одиночная волна.

Для сравнения влияния формы затупления на образование волны проведён аналогичный расчёт (с теми же значениями модельных параметров) для цилиндра с плоским затуплением «головной» части. Построенные по результатам обоих численных экспериментов графики изменения уровня свободной поверхности в точке r = 0,2 практически совпадают, о чем свидетельствует рисунок 3. Разница состоит лишь в том, что волна, образованная погружением цилиндра с плоским затуплением, приходит в точку r = 0,2 раньше. Таким образом, процесс образования волны при полусферическом затуплении протекает медленнее, и связано это с тем, что сначала жидкость движется вдоль полусферической поверхности цилиндра. В случае же с плоским затуплением волна образуется сразу, как только тело вступает в контакт с жидкостью.

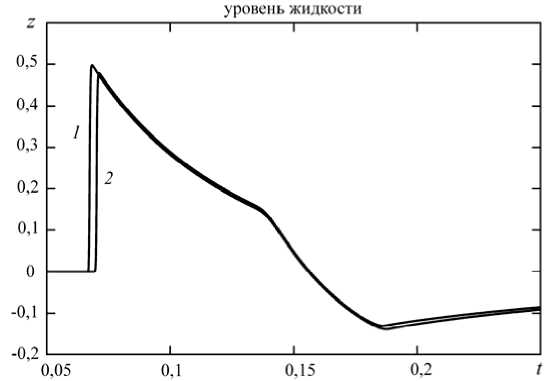
Рис. 3. Изменение уровня свободной поверхности в точке r = 0,2 в зависимости от формы затупления «головной» части цилиндра при значениях параметров R_b = 0,1 , V_{b ,0} = 30 : плоский торец (кривая 1 ); полусферическое затупление ( 2 ).

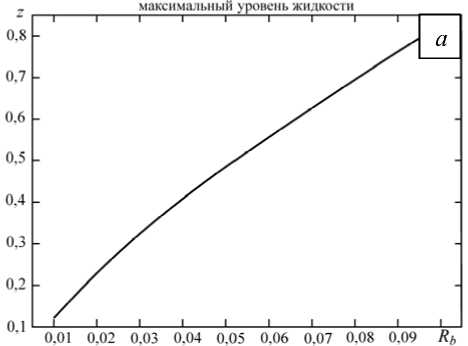
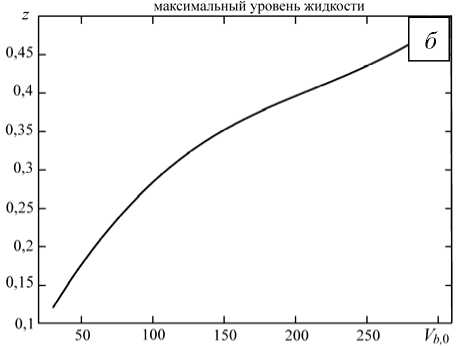
Рис. 4. Зависимость максимального значения амплитуды образованной волны от радиуса ( а ) и начальной скорости ( б ) цилиндра с полусферическим затуплением

Исследуем влияние радиуса цилиндра и его начальной скорости на амплитуду образованной волны. Поскольку форма затупления «головной» части не влияет на образование волны, во всех последующих расчётах рассматривается только цилиндр с полусферическим затуплением.

На рисунке 4, а показан график зависимости максимального уровня свободной поверхности от радиуса цилиндра R b е [ 0,01; 0,1 ] при начальной скорости погружения V b ₀ = 30. Из рисунка 4, а видно, что максимальный уровень свободной поверхности находится в прямой зависимости от радиуса погружающегося тела, и чем больше радиус, тем большее уровень жидкости.

Влияние начальной скорости погружения цилиндра изображено на рисунке 4, б . График получен при расчётах с параметром R b = 0,01 и начальной скоростью погружения V_b0 е [ 30;300 ] . Здесь также видно, что чем больше начальная скорость цилиндра, тем больше максимальное значение амплитуды образованной волны. Совершенно ясно, что такая зависимость объясняется прямой связью: тело с бóльшей кинетической энергией вызывает бóльшее возмущение свободной поверхности. Рассмотрение этой зависимости в размерных величинах показывает, что, например, при погружении тела с радиусом в 10 м и начальной скоростью в 25 км/с в слой жидкости глубиной в 1 км образуется волна с амплитудой более 400 м.

Выясним, как параметры погружающегося тела связаны с понижением амплитуды A ([9]) образованной волны. В таблице представлены максимальные значения уровня свободной поверхности в точках r = 0,1; 0,2; 0,3; 0,4. В последней колонке находятся процентные отношения значения амплитуды в точке r = 0,4 к её же значению в точке r = 0,1. Видно, что понижение амплитуды отличается для волн, образованных при разных значениях модельных параметров, причём для тел с равными радиусами R_b понижение амплитуды происходит быстрее при бóльших V_{b ,0} . Из сравнения вычислительных экспериментов 1 и 3 следует, что, несмотря на соответствие бóльшему R_b более высокой амплитуды образованной волны, понижение происходит схожим образом, то есть соответствующие этим экспериментам процентные отношения примерно совпадают. Всё это может говорить о том, что наиболее «катастрофичные» для удалённых объектов волны образуются при погружении тела с бóльшими размерами. Расчёты также показывают, что нельзя пренебрегать сопротивлением жидкости: понижение амплитуды волн, образованных с учётом сопротивления, происходит быстрее (см. эксперименты 3 и 4).

Таблица. Понижение амплитуды образованной волны

Номер вычислительного эксперимента	Модельные параметры	r				А ^ -% А ( r 1 )
		r = 0,1	r = 0,2	r 3 = 0,3	r , = 0,4
		Значения уровня с учётом сопротивления
1	R b = 0,07, V b ,0 = 30	0,470	0,269	0,193	0,151	32
2	R b = 0,05 V b ,0 = 100	0,485	0,252	0,173	0,132	27
3	R b = 0,05 V b ,0 = 30	0,263	0,152	0,102	0,087	33
		Значения уровня без учёта сопротивления
4	R b = 0,05 V b ,0 = 30	0,373	0,265	0,207	0,162	43

• 5.    Заключение

Проведённые вычислительные эксперименты показали, что при погружении твёрдого цилиндрического тела в невозмущённую жидкость образуются волны, амплитуда которых находится в прямой зависимости от его радиуса и скорости. При этом влияние размера тела сказывается в бóльшей степени, чем влияние начальной скорости.

Построены зависимости максимальных значений амплитуды образованных волн от параметров тела. Проведено сопоставление распространения образованных волн с учётом и без учёта сопротивления жидкости, которое выявило особенности, позволившие сделать вывод: сопротивлением жидкости погружению твёрдого тела пренебрегать недопустимо.

Расчёты показали, что форма затупления погружающегося цилиндра не влияет на образование волны и её динамику. При расчётах форму «головной» части погружающегося тела можно не учитывать. Однако следует помнить, что при наличии у цилиндра плоского затупления образование волны происходит быстрее, чем при его полусферическом затуплении.

Хотя в рассмотренном процессе ключевым параметром, способствующим образованию волны с большой амплитудой, является размер тела, а именно радиус цилиндра, для образования катастрофически больших волн необходима огромная скорость его движения. Такой скоростью обладают тела из межпланетного пространства, и их падение в открытый океан является вполне реальным механизмом образования разрушительных волн.

Работа выполнена при финансовой поддержке РФФИ   (проект

№ 11-01-98510-р_восток_а) и ДВО РАН (проекты № 09-1-П17-03, 11-III-В-03-037).