Численное исследование процесса распылительной сушки молока

DOI:

*Казанский национальный исследовательский технологический университет, г. Казань, Россия; e-mail: , ORCID:

Харьков В. В. и др. Численное исследование процесса распылительной сушки молока. Вестник МГТУ. 2025. Т. 28, № 2. С. 263–272. DOI:

e-mail: , ORCID:

Kharkov, V. V. et al. 2025. Simulation of milk spray drying. Vestnik of MSTU, 28(2), pp. 263–272. (In Russ.) DOI:

Молоко является сбалансированным, легкоусвояемым и ценным продуктом питания, который играет важную роль в рационе человека благодаря его богатому химическому составу. В молоке содержится полный комплекс незаменимых аминокислот (лизин, лейцин, тирозин и др.), витаминов (А, В₁, B₂, B₁₂, D), микроэлементов (кальций, магний, калий) и других нутриентов. Оно является основным сырьем для изготовления множества различных молочных продуктов. Потребление молока и молочных продуктов населением при соблюдении суточной нормы является частью здорового и диетического питания ( Zhang et al., 2021; Milk…, 2013 ).

Цельное молоко является общепризнанно полезным для детей и подростков для роста и развития организма, но его неконтролируемое потребление может быть потенциально вредным для взрослых и пожилых людей из-за высокого содержания насыщенных жиров. В данном случае наилучшим заменителем цельного молока выступает обезжиренное молоко. Обезжиренное молоко – это молочный продукт с пониженным содержанием жира (0–1 %), изготовленный из цельного молока путем отделения сливок, т. е. обезжиренное молоко является отходом производства сливок. Поэтому дальнейшее использование этого молока непосредственно в пищевых целях или в качестве сырья в рецептуре других молочных продуктов является важным элементом безотходной технологии молокоперерабатывающих предприятий. Так как сухая форма молока отличается длительным сроком хранения и возможностью полной автоматизации процесса, то такая форма является предпочтительной при утилизации обезжиренного молока.

Согласно ГОСТ 333629-20151 сухое обезжиренное молоко – это концентрированный продукт, полученный посредством распылительной сушки обезжиренного молока, предназначенный для пищевых целей или дальнейшей переработки. Сухое обезжиренное молоко широко используется как полноценный аналог свежего молока, так как при правильно проведенном технологическом процессе практически полностью сохраняется пищевая ценность и вкусовые характеристики исходного (свежего) молока. Сухое обезжиренное молоко является важным ингредиентом не только в молочной промышленности, но и в кондитерской, хлебобулочной, масложировой, фармацевтической и других отраслях.

В свое время изобретение технологии распылительной сушки произвело революцию в молокоперерабатывающей промышленности ( Jakkamsetty, 2024 ). По сравнению с другими способами сушки она отличается высокой скоростью процесса и отсутствием прямого контакта продукта с нагретыми поверхностями сушилки ( Белецкая и др., 2019 ), что способствует сохранению полезных веществ молочных продуктов ( Харьков и др., 2017а ).

Получение сухого продукта в распылительной сушильной установке зависит не только от теплового режима, но и от гидрогазодинамики внутри установки, способа распыла жидкости, ее дисперсности, теплофизических свойств среды. Поэтому исследование процесса распылительной сушки не является простым. В работе ( Wadud Ahmed et al., 2024 ) в качестве детерминирующего фактора при сушке выбрано время пребывания распыленных капель в сушильной камере. Получено распределение времени пребывания обезжиренного молока при различных режимных параметрах работы распылительной сушилки. Авторы ( Михалева и др., 2010 ) проанализировали гидродинамические характеристики частиц в процессе распылительной сушки жидких молочных продуктов с целью оптимизации процесса, увеличения выхода готового продукта и улучшения его качества. Представлена математическая модель движения капель молока в газовзвешенном режиме сушки. Выполнено исследование работы пульсатора, обеспечивающего возвратно-поступательное движение греющего газа в сушильной установке. В работе ( Муродова, 2024 ) проведена оптимизация работы распылительной сушилки молока для определения оптимальных режимов ее работы. Найдено, что низкотемпературный режим сушки и контроль влажности способствуют значительному улучшению качества, сохранению питательных веществ и повышению однородности молочного порошка.

Ведутся также исследования по интенсификации распылительной сушки с помощью различных электрофизических методов. В работе ( Dantas, 2024 ) проведен сравнительный анализ модифицированных методов распылительной сушки (пульсационный, электростатический, нано-, экструзионно-пористый), на основе которого выявлены их ограничения и даны рекомендации по дальнейшим исследованиям. Авторами ( Беззубцева и др., 2019 ) предложен метод распылительной сушки молока с использованием ультразвуковых технологий для повышения эффективности термического обезвоживания и качества получаемого сухого продукта. Установлено, что при определенной мощности ультразвуковых колебаний формируются сферические шарообразные капли диаметром приблизительно 1,0 мм. Также выявлено, что производительность распыления жидкости под действием ультразвука зависит от давления насыщенных паров и коэффициентов динамической вязкости, а также поверхностного натяжения жидкости.

При моделировании распылительной сушки необходимо учитывать изменение скорости сушки с течением времени. На данный момент существует классификация основных моделей, описывающих кинетику сушки капель, содержащих твердые включения ( Poozesh et al., 2018 ):

• 1)    модели, в которых описываются изменения средней температуры и влагосодержания частицы без учета их морфологической эволюции в течение сушки. Репрезентативными моделями являются

  полуэмпирическая модель CDC (Characteristic Drying Curve), в которой используется характеристическая кривая для скорости сушки, зависящей только от среднего влагосодержания частицы ( Langrish et al., 2001 ), и механистическая модель REA (Reaction Engineering Approach), представленная в работе ( Chen et al., 1997 ), в которой весь процесс сушки рассматривается как конкурирующий реакционный процесс между испарением и конденсацией. Ограничением REA модели является необходимость установления связи между энергией активации и влагосодержанием частицы в процессе сушки. Позднее авторы ( Chen et al., 1999 ) усовершенствовали эту модель, включив учет сопротивления переносу массы при наличии сухой корки. В работе ( Schmitz-Schug et al., 2016 ) было выполнено численное моделирование распылительной сушки молочных продуктов на основе REA модели. Показано, что связь свойств частиц с кинетикой нежелательных реакций позволяет улучшить качество высушенного продукта. В работе ( Putranto, 2016 ) приведены различные параметры кинетики сушки по подходу REA для различных пищевых продуктов. Сравнение результатов моделирования сушки углеводов, выполненное авторами ( Woo, 2008 ), показало, что подход REA может быть использован для оценки влажности поверхности частиц, которая может влиять на процесс их агломерации;

• 2)    детерминистические модели, описывающие процесс формирования частиц, включая рост и агломерацию дисперсных частиц, что приводит к кристаллизации капли во время процесса сушки. Представителем этой группы моделей является подход, представленный в работе ( Nesic et al., 1991 ), в котором выявлено пять последовательных стадий процесса распылительной сушки, через которые проходит одиночная капля, включающая растворенные или взвешенные твердые включения, а именно: подогрев и испарение, квазиравновесное испарение, образование корки и ее рост, кипение и сушка пористой частицы. Приведены критерии перехода между этими стадиями в виде условий, при которых заканчивается одна и начинается другая стадия испарения. Основным недостатком данного подхода является необходимость определения соответствующих коэффициентов диффузии. Другим представителем этой группы моделей является модель усадки (или сокращения диаметра) ядра, в которой процесс сушки разделен на период постоянной скорости сушки и период падающей скорости сушки. В рамках данного концепта в работе ( Mohammed, 2003 ) описывается модель распылительной сушки капель с твердыми включениями с учетом отступающей границы (фронта) испарения, которая разделяет области влажного ядра и сухой корки частицы. Постулатом служит предположение, что кинетика сушки полностью определяется диффузионными процессами внутри частицы и сопротивлением внешней конвекции. Игнорирование температурой фронта испарения ограничивает применимость данной модели сушки.

Высокая стоимость распылительной сушилки и вспомогательного оборудования (насос, вентилятор, калорифер, циклон, фильтр и т. д., средства контроля и автоматизации), затраты на проведение пусконаладочных работ и сервисное обслуживание, сложности при проведении точных измерений параметров дисперсной фазы и греющего газа – все это сильно ограничивает возможность проведения экспериментальных исследований процесса сушки. Хорошей альтернативой при проектировании распылительных установок, их модернизации и научного всестороннего исследования является использование современных инструментов компьютерного моделирования (CFD), позволяющих сымитировать реальный процесс на основе существующих сложных моделей кинетики сушки капель растворов и распыла даже при изменении конструктивных характеристик оборудования и режимов параметров его работы ( Харьков и др., 2018 ).

Целью работы является численное исследование процесса распылительной сушки капель обезжиренного молока на основе модели усадки ядра.

Материалы и методы

Модель сушки одиночных сферических капель, содержащих твердых включения, используемая в этом исследовании, является механистической моделью усадки ядра, основанной на отступании фронта испарения, которая включает четыре последовательные стадии сушки: стадию нагрева, квазиравновесное испарение, формирование корки (и кипение), сушка пористой частицы. Детальное математическое описание модели с принятыми допущениями представлено в работах ( Харьков и др., 2023; Харьков и др., 2024 ). Характерной особенностью данной модели является то, что она дает детальную информацию о распределении влаги и твердых включений, а также температуры внутри капли в процессе термического обезвоживания в дисперсном виде. Показательно, что предлагаемая модель сушки капель суспензий является физической, а не эмпирической.

Численное исследование выполнено с использованием CFD продукта открытого кода OpenFOAM 11. Для описания характеристик движения газовой фазы использовались осредненные по Рейнольдсу уравнения Навье – Стокса, тогда как для дисперсной фазы – подход Лагранжа. Для замыкания системы уравнений для турбулентного течения газа применялась стандартная k-ε модель. Учет взаимного влияния фаз основан на методе двусторонней связи ( Farid, 2003 ).

В качестве расчетной геометрической области был выбран параллелепипед длиной 0,1 м в плоскости XY и 0,01 м в плоскости XZ. Построена равномерная гексагональная сетка с размерами 50×100×50. Поток греющего газа постоянной температуры поступает из нижней части. Капля диаметра Dк вводится в центр вычислительной области с нулевой начальной скоростью в момент времени t = 0 с. Так рассматриваемая капля зафиксирована во взвешенном состоянии в потоке встречного греющего газа. Масса капли mк рассчитывается в зависимости от ее плотности и диаметра. Для решения уравнений сохранения массы и тепла внутри капли в процессе распылительной сушки используется явный метод конечных разностей. Для этого была разработана одномерная сферическая конечно-разностная расчетная схема, в которой полный объем капли разбивается на 50 оболочек одинаковой толщины.

При изучении кинетики сушки капель обезжиренного молока предполагается, что летучим компонентом капель молока является вода. Физико-химические свойства порошка молока взяты из ( Pugliese et al., 2017 ). В качестве греющего газа использовался воздух. Необходимые параметры моделирования перечислены в таблице.

Таблица. Начальные данные Table. Initial data

Содержание сухих веществ w св, % масс.	Плотность жидкости ρ, кг/м3	Начальный диаметр капли D к, мм	Скорость греющего газа V г, м/с	Температура греющего газа T г, K
20	1 234	1,76 и 1,71	0,75	323 и 363
Коэффициент диффузии корки D кор , м2/с	Коэффициент теплопроводности корки k кор , Вт/м∙К	Коэффициент теплопроводности ядра k ядро , Вт/м∙К	Температура капли T к , K	Концентрация насыщения (растворимость) S *, кг/кг
1,5∙10–6	0,07	0,372	289	0,50

Результаты данного численного исследования процесса сушки капель обезжиренного молока по предлагаемой модели сушки сравниваются с данными из экспериментальной работы ( Nesic et al., 1991 ).

Средняя температура капли T̅ (К) рассчитывалась интегрированием локальной температуры капли T (К) в радиальном направлении капли r по следующему выражению:

r

T = - J r² T ( r ) dr.                                         (1)

r ₀

Температура на поверхности капли T пов (К) была рассчитана с помощью уравнений 2 и 3 в зависимости от периода сушки:

• •    для периода постоянной скорости сушки

  д T

  д t

  
  

  а д ₂дT т -I r ~ r ² д r I д r

  
  

  при ^- k — = h ( T™ ^- T L ) ^,r = R ; д r

  
  
  
  

• •    для периода падающей скорости сушки

dT   1  ^KRNuyT-TJ + Lmn dt  mCv   у ! Nu\   5        dt

2k R -5 _             кор кр где t – время сушки, с; a – температуропроводность капли, м2/с; h – коэффициент теплоотдачи, Вт/м2·K; CV – теплоемкость жидкости, Дж/кг·K; Nu – число Нуссельта; λГ – коэффициент теплопроводности газа, Вт/м∙К; T∞ – температура на отдалении от поверхности капли, К; Rкр – критический радиус (радиус после усадки), м; δ – толщина корки, м; L – скрытая теплота парообразования, Дж/кг.

Коэффициент диффузии для капли обезжиренного молока был рассчитан с помощью следующего уравнения ( Wijlhuizen et al., 1979 ):

D = exp

38912 + 32339w в 1 + 1584w_e

где w в – влагосодержание капли, кг воды/кг сухих веществ.

Результаты и обсуждение

На рис. 1–2 показаны результаты численного расчета сушки одиночных капель обезжиренного молока при температуре греющего газа 323 К. В общем случае, временной процесс сушки складывается из двух последовательных периодов – период с постоянной скоростью сушки сменяется периодом падающей скорости сушки. Стоит отметить, что кривые сушки капли для этих периодов различны. Начало периода падающей скорости сушки наблюдается при t = 125 с, когда возникают новые сопротивления явлениям переноса из-за образования сухой корки, которые приводят к замедлению процесса сушки. Причем это падение скорости сушки прямо пропорционально наклону кривой потери массы капли (рис. 1). Возможно, это вызвано тем, что коэффициент теплопроводности влажного ядра высушиваемой частицы примерно в 6 раз больше коэффициента теплопроводности для пористой корки.

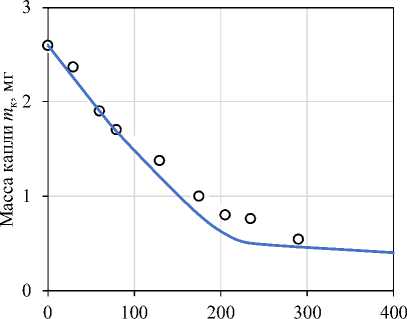
Время сушки t , с

Рис. 1. Изменение массы капли при T _г = 323 K: линия – расчет; точки – эксперимент

Fig. 1. Change in droplet mass at T gas = 323 K: line – simulation; points – experiment

Согласно временной зависимости изменения температуры капли при температуре греющего газа T _г = 323 K и основываясь на принятой морфологической модели кинетики сушки, на рис. 2 могут быть выделены четыре различные стадии сушки:

• •    начальный период, соответствующий прогреву капли (0–15 с);

• •    квазиравновесное испарение (15–125 с);

• •    формирования корки (125–280 с);

• •    сушка пористой частицы (280–400 с).

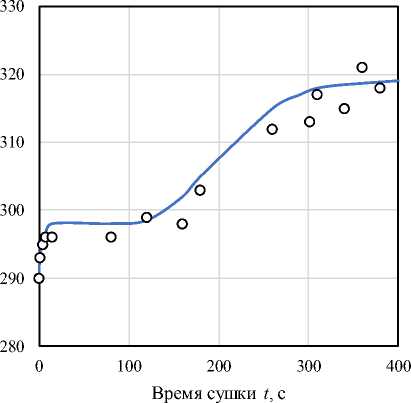
Рис. 2. Изменение температуры капли при T г = 323 K: линия – расчет; точки – эксперимент Fig. 2. Change in droplet temperature at T _gas = 323 K: line – simulation; points – experiment

Кривая кинетики сушки показывает, что на второй стадии, соответствующей периоду с постоянной скоростью сушки, происходит интенсивное удаление свободной влаги с поверхности капли при небольшом изменении ее температуры. На следующей стадии (период падающей скорости сушки) наблюдается постепенное увеличение температуры одиночной капли обезжиренного молока. Здесь формирование сухой корки на поверхности капли приводит к значительному снижению интенсивности удаления влаги из капли. На заключительной стадии сушки удаляется связанная влага, поэтому наблюдается небольшая скорость сушки.

Для оценки влияния температуры греющего газа на процесс сушки обезжиренного молока также было проведено численное моделирование этого процесса в соответствии с предлагаемой моделью при

T _г = 363 K. Согласно рис. 3–4 при более высокой температуре газа на входе скорость сушки увеличивается, и весь процесс протекает быстрее приблизительно в 2 раза.

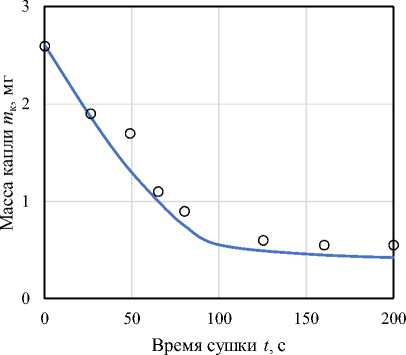
Рис. 3. Изменение массы капли при T г = 363 K: линия – расчет; точки – эксперимент Fig. 3. Change in droplet temperature at T gas = 363 K: line – simulation; points – experiment

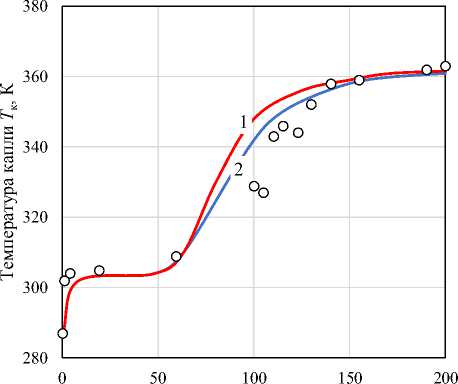
Время сушки t , с

Рис. 4. Изменение температуры капли при T _г = 363 K: линия (1) – расчетная температура на поверхности капли; линия (2) – расчетная осредненная температура; точки – эксперимент

Fig. 4. Change in droplet temperature at T _gas = 363 K: line (1) – calculated temperature on the droplet surface; line (2) – calculated averaged temperature; points – experiment

Для случая когда T г = 323 K, время до резкого повышения температуры капли составляет приблизительно 120 с, в то время как соответствующее значение при T г = 363 K – около 70 с. Так как высокая температура греющего газа может негативно повлиять на качество готовой продукции ( Харьков и др., 2017б ), отмечается, что даже при повышенной температуре греющего газа на кривой сушки отсутствует кипение.

Согласно рис. 4 также можно различить четыре последовательные стадии сушки:

• •    начальный период, соответствующий прогреву капли (0–10 с);

• •    квазиравновесное испарение (10–50 с);

• •    формирование корки (50–140 с);

• •    сушка пористой частицы (140–200 с).

Сокращение общего времени сушки при повышении температуры греющего газа происходит в основном за счет уменьшения продолжительности стадий квазиравновесного испарения (на 63,6 %) и формирования корки (на 50 %).

Результаты численного расчета по принятой модели (рис. 4) также показывают, что температура на поверхности капли, начиная со стадии формирования корки, превышает осредненную температуру капли. Наибольшая разница температур наблюдается в период времени t = 70–120 с и составляет в среднем 8,5 %. В конце периода падающей скорости сушки значения осредненной температуры капли и температуры на поверхности капли выравниваются. Это связано с тем, что диаметр (и объем) влажного ядра, имеющего более низкую температуру, чем сухая корка, уменьшается. Соответственно, снижается вклад температуры влажного ядра при расчете осредненной температуры частицы.

Анализ полученных зависимостей, представленных на рис. 1–4, позволяет сделать вывод, что имеется удовлетворительное согласование между результатами численного расчета по реализованной модели сушки и экспериментальными данными ( Nesic et al., 1991 ) при различных условиях распылительной сушки капель обезжиренного молока. В частности, относительная ошибка между экспериментальными и расчетными значениями массы капли при температурах греющего газа 323 и 363 К в процессе сушки составляет в среднем 10,7 %, а средняя абсолютная погрешность для осредненной температуры капли – не более 5 K.

Далее на основе валидной математической модели проведены численные расчеты распределений температуры и влагосодержания внутри одиночной капли/частицы во время распылительной сушки.

Согласно рис. 4 в период постоянной скорости сушки температура внутри одиночной капли изменяется незначительно. На рис. 5, а показаны температурные профили внутри одиночной капли обезжиренного молока с начальным диаметром 1,71 мм для различных моментов времени от 72,5 до 199,3 с, соответствующих периоду падающей скорости сушки при температуре воздуха 363 K. Отмечается, что увеличение толщины сухой пористой корки приводит к повышению сопротивления теплопередачи, так как увеличивается разница между температурой на поверхности капли и температурой влажного ядра. Для всех случаев вначале наблюдается линейная зависимость температуры капли от радиуса r , затем она становится выпуклой. Это может быть связано с тепловым эффектом паров, диффундирующих через поры корки, так как согласно рис. 5, б влагосодержание частицы в начале падающего периода сушки еще небольшое. Зависимости на рис. 5, б показывают, что в процессе падающей скорости сушки значение граничной концентрации влаги (максимальной концентрации для каждой кривой) увеличивается, так как она рассчитывается на основе температуры на границе влажное ядро – корка, которая постепенно растет из-за влияния теплопроводности.

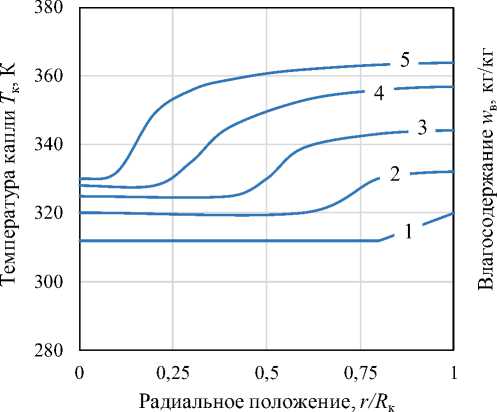
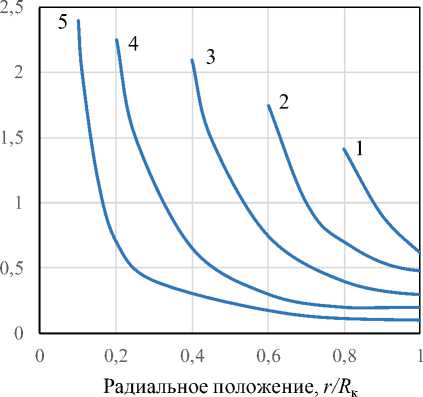
а                                                б

Рис. 5. Профили температуры ( а ) и влаги ( б ) внутри капли ( T г = 363 K, D к = 1,71 мм) в зависимости от времени t , с: 1 – 72,5; 2 – 79,8; 3 – 99,7; 4 – 152,1; 5 – 199,3 Fig. 5. Temperature ( a ) and moisture ( б ) profiles inside a droplet ( T gas = 363 K, D d = 1.71 mm) depending on time t , s: 1 – 72.5; 2 – 79.8; 3 – 99.7; 4 – 152.1; 5 – 199.3

Заключение

На основании выполненной работы можно сделать следующие выводы:

• •    результаты численного моделирования процесса распылительной сушки капель обезжиренного молока на основе механистической модели усадки ядра при различных режимных параметрах удовлетворительно сходятся с экспериментальными данными (относительная погрешность для массы капли составляет в среднем 10,7 %, а абсолютная погрешность для осредненной температуры капли – не более 5 K);

• •    данная модель кинетики сушки позволяет оценивать изменение температуры и влагосодержания частицы во время сушки в дисперсном виде, что обычно пренебрегается в других подходах;

• •    валидная модель кинетики сушки может быть использована для моделирования процесса распылительной сушки капель разного диаметра различных суспензий и растворов в периоды постоянной и падающей скорости сушки.

В дальнейшем планируется провести прогнозирование работы полупромышленной распылительной сушилки на основе разработанной математической модели кинетики сушки, чтобы оценить возможность ее использования в реальных условиях при производстве сухого обезжиренного молока.