Численное моделирование динамических систем со случайными запаздываниями

Современные инструменты математического моделирования, наряду с иными, включают различные формы уравнений с последействием (запаздыванием, лагом): дифференциально-разностные уравнения (ДРУ), дифференциальные уравнения с отклоняющимся аргументом, уравнения с запаздыванием, нейтральные уравнения [1-7] и т. д. Реальные явления могут моделироваться системами уравнений весьма сложной структуры, в т.ч. гибридные системы дифференциальных уравнений (в обыкновенных и в частных производных) [8-10], системы с переменной структурой [И-14] , включающие уравнения с последействием, содержащими несколько дискретных лагов, распределенные и случайные запаздывания и их иные комбинации.

Стохастические обыкновенные дифференциальные уравнения (СОДУ) с постоян-

ным запаздыванием и, в частности, дифференциально-разностные уравнения, являются обобщениями и детерминистических уравнений с постоянным запаздыванием, и стохастических обыкновенных дифференциальных уравнений [15-18].

Модели с переменным лагом являются более сложными, и, как правило, у них отсутствуют аналитические решения в замкнутой форме. Поэтому для интегрирования даже неслучайных ДРУ требуются приближенные численные процедуры, а анализ явлений с изменяющимся запаздыванием является в основном количественным. Дополнительный уровень адекватности моделей (но и усложнения тоже) можно получить, если перейти от неслучайных к стохастическим моделям.

Еще более сложными становятся модели различных процессов, в которых требуется трактовка запаздываний как случайных величин и функций. В частности, модели такого вида возникают при описании систем, меняющих свою структуру под воздействи- ем случайных факторов. Несмотря на широкое поле приложений в физике, биологии, экономике, финансах, системах управления, технологии и др. (см. обзорную частв работ [19,20]), уравнения подобного вида недостаточно исследованы.

Чтобы решать многочисленные пробле-мв1, необходимо строить математические модели случайных лагов, которые выбираются в форме независимых случайных величин, однородных и неоднородных, дискретных и непрерывных цепей Маркова, скрытых цепей Маркова, а также в виде более общих стационарных и нестационарных случайных процессов, в том числе и функций векторов состояния динамических систем.

Вследствие сложности задач методы исследования стохастических систем со случайными запаздываниями нетривиальны и немногочисленны. Прямые аналитические схемы анализа таких систем типа уравнения Фоккера-Планка-Колмогорова (ФПК-уравнения) [21, 22], как правило, отсутствуют, а приближенные ориентируются на исключение случайного запаздывания или полностью, или сведением к системам с неслучайным постоянным или переменным запаздыванием.

На практике целью построения численных интеграторов для СОДУ, СОДРУ и других классов стохастических уравнений [23,24], кроме построения реализаций переходных процессов, является вычисление (после дискретизации этих уравнений) с использованием метода статистического моделирования (Монте-Карло) [25] сеточных представлений {X k} к = 1 , 2 , ...,N ) мно жества реализаций x ( t ) вектора состояния системы в узлах сетки, которые служат для оценки вероятностных характеристик вектора X ( t ) на основе методов математической и прикладной статистики.

Трудности с решением задачи прямого численного моделирования различных систем со случайными запаздываниями частично могут быть сняты при использовании современных математических пакетов, таких как Maple [26], Mathematica [27], Matlab [28], Maxima [29] и др. В данной работе дан обзор как общих возможностей математического пакета Mathematica в области реше ния задач вероятностно-статистического направления, так и некоторые новые средства этого пакета, которые можно использовать для моделирования динамических систем с различными формами случайных запаздываний. В работе приведены примеры расчета переходных режимов, представлены фрагменты программ для таких расчетов и результаты последних.

1.    Вероятность, статистика и случайные процессы в пакете Mathematica

Mathematica - коммерческая интегрированная система (пакет) компьютерной алгебры (КА), изначально задуманная С. Вольфрамом (Stephen Wolfram), разработанная собранной и руководимой им командой математиков и программистов и продаваемая его компанией Wolfram Research Inc. Mathematica - также язык программирования, реализующий наилучшим образом множественную систему взглядов и понятий на основе правил подстановок.

Появление пакета в 1988 г. оказало очень большое влияние на использование компьютеров в науке и технике. Часто говорят, что именно появление системы Mathematica, наряду с реализацией новых прорывных идей, вобравшей лучшие черты предыдущих систем КА, таких как Macsima, Reduce, SMP, Maple, открыло современную эру применения компьютерной алгебры в научных и технических вычислениях. Концепция CAB Mathematica с самого начала и навсегда была заявлена как ориентация на создание единой системы, которая могла бы отслеживать различные аспекты научнотехнических расчетов логически последовательным и унифицированным способом. Ключевым интеллектуальным достижением пакета явилось создание языка компьютерной алгебры, который позволяет обрабатывать широкий спектр объектов с помощью небольшого числа базовых схем. Mathematica является ведущим программным продуктом для обработки числовых, символьных и графических данных, повсюду используемым профессионалами практически в каждой ветви научных и технических вычислений.

Среди общих групп функций пакета отметим наличие процедур, предназначенных для: аналитических преобразований; численных расчетов с произволвной точноствго; решения задач алгебры, математического анализа, вычислительной математики и др.; работы с графикой и звуком; финансовых расчетов; анализа текстов; импорта и экспорта фильтров, предназначенных для различных форматов данных, изображений, видео, звука, CAD, GIS, документов и др.; разработки программного обеспечения и т.п.

Для решения задач теории вероятностей (ТВ), математической и прикладной статистики (МС, ПС), теории случайных процессов (ТСП) и последовательностей также имеется широкий набор средств, позволяющий системе Mathematica успешно конкурировать со специализированными статистическими пакетами, что показывает и включение пакета в List of statistical packages [30].

В языке пакета Mathematica символьные распределения и процессы используются в качестве моделей для случайных величин и случайных процессов. Эти модели, построенные на базе богатой библиотеки встроенных аналитических распределений и процессов, могут использоваться для обработки статистических данных и построения расчетных программ анализа сложных переходных процессов.

Если коротко, то множество функций (версия пакета: Mathematica 12), реализующих структуры ТВ, МС и ПС, включает процедуры:

• -    задания одномерных и многомерных непрерывных, одномерных и многомерных дискретных (соответственно 70 и 8, 20 и 6), а также специальных (9) распределений случайных величин;

• -    символьных и численных расчетов вероятностей событий, характеристической функции (ХФ), функции распределения (ФР) и обратной к ней, плотности вероятности (ПВ), начальных и центральных моментов, в т.ч. математического ожидания и дисперсии, среднего квадратичного отклонения (СКО), кумулянтов, медианы, коэффициента асимметрии, эксцесса, квантилей, в частности квартилей, интерквартильной широты для каждого одномерного распре

деления;

• -    подобные указанным выше (с добавлением специфичных для случая многих случайных величин) для каждого многомерного распределения;

• -    описательной статистики;

• -    расчета точечных и интервальных оценок параметров распределений;

• -    преобразования и сглаживания экспериментальных данных;

• -    проверки гипотез;

• -    регрессионного и дисперсионного анализа, кластерного анализа, распознавания образов;

• -    генерирования псевдослучайных чисел (ПСЧ) по дискретным и непрерывным распределениям;

• -    мощной статистической графики.

Теперь остановимся на средствах работы со случайными процессами (СП). Такие процессы моделируют изменение систем во времени, причем эволюция является случайной, а не детерминированной. Ключевым моментом является то, что сечения процессов, которые близки по времени, являются зависимыми, и это должно учитываться и использоваться для моделирования, имитации и прогнозирования поведения процесса.

Основываясь на мощной символьной и численной поддержке стандартных средств, язык пакета обеспечивает целостную и всестороннюю поддержку анализа случайных процессов, включающего моделирование поведения, оценку параметров на основе статистики и вычисление вероятностей состояния в разное время. Существует дополнительная возможность исследования для специальных классов случайных процессов, таких как цепи Маркова, очереди, временные ряды и стохастические дифференциальные уравнения.

Средства пакета для работы со СП объединены в следующие (частично пересекающиеся) группы:

• 1 °. Симулирование и оценка параметров (построение траекторий случайных процессов, формирование временных рядов по имеющимся данным, подгонка теоретического СП под данные, обработка статистики по СП).

• 2 °. Вероятностные распределения процес-

• сов (вычисление вероятностей, оценка сечений, стационарные распределения, получение условий для параметров теоретического СП, проверка правильности задания СП).

• 3 °. Вычисление моментных характеристик СП (функции математического ожидания, ковариационной и корреляционной функций), проверка на стационарность в широком смысле.

• 4 °. Теоретические модели случайных процессов:

• -    параметрические СП (с дискретным временем и дискретными состояниями; с дискретным временем и непрерывными состояниями: дискретный белый шум, составной процесс восстановления, преобразованные процессы; с непрерывным временем и дискретными состояниями; с непрерывным временем и непрерывными состояниями);

• -    производные СП (белый шум, преобразованные процессы; потоки событий: простой и составной процессы восстановления, составной пуассоновский процесс; процессы обслуживания);

• -    марковские процессы (модели марковских процессов: марковские цепи с дискретным и непрерывным временем, скрытая марковская модель; свойства: структурные, переходные и предельные состояния и др.; структура случайных процессов; проверка свойств моделей; обработка временных рядов и др.);

• -    процессы, описываемые СОДУ (специальные диффузионные процессы: винеровский процесс, процесс Орнштейна-Уленбека, броуновский мост, геометрическое броуновское движение, процесс Кокса-Ингерсола-Росса; общие диффузионные процессы: решение СОДУ Ито, решение СОДУ Стратоновича).

2.    Стохастическая системабез запаздывания

• 0.9 Sin [t + w[t]] , w ~ WienerProcess[ ], t];

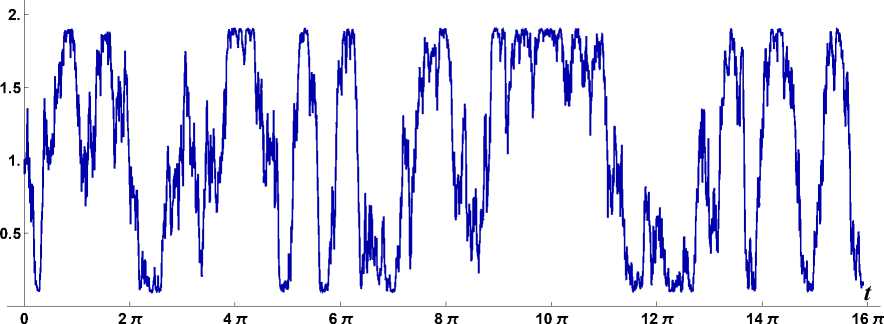
Для начала рассмотрим средства моделирования (псевдо)случайных возмущений в стохастических уравнениях. Для этого построим модель ограниченного шума [31] на основе стандартного винеровского процесса и воспользуемся следующими командами пакета Mathematica:

Т = 50; h = 0.001; nt = 50000;

ql = TransformedProcess[1 -

Ql = Interpolation[RandomFunction [ql, 0, T, h]];

График реализации случайной функции, обозначенной Ql, приведен на рис. 1.

Теперь оценим влияние шума рассмотренного типа на колебательную систему, описываемую уравнением Дюффинга типа:

X ( t ) + 2 aX(t ) + w 02 X ( t ) +

+ вХ 3 (t) = 4 Q 2( t), где a, w, в ~ постоянные. Для этого предназначен следующий фрагмент программы:

q2 = TransformedProcess[Sin[t + w[t]], w ~ WienerProcess[ ], t];

• Q2 = Interpolation[RandomFunction

• [q2, 0, T, h]];

3.    Системы с запаздыванием

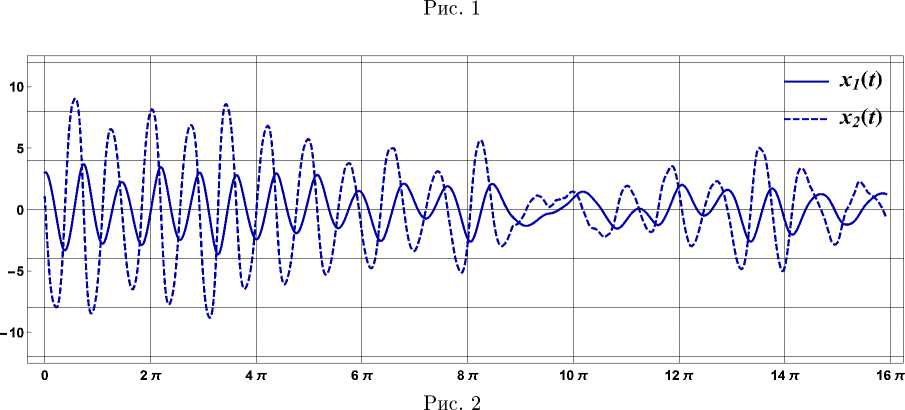
sol2 = NDSolve[ xl’[t] == x2[t], x2’[t] == -0.1 x2[t] - 4 xl [t] -xl[t]~3/2 + 4 Q2[t], xl[0] == 3, x2[0] == 1, xl[t], x2[t], t, 0, T] где введены обозначения X i ( t ) = X ( t ), X 2 ( t ) = X ( t ), а для численного интегрирования системы используется встроенная функция NDSolve. Графики реализаций случай ных функций X i ( t ) 11 X 2 ( t ) приведены на рис. 2.

Теперь рассмотрим системы с различными формами случайного запаздывания. Все они, если не считать запаздывание, являются детерминированными по форме. Поэтому, с одной стороны, ничто не может помешать использовать стандартные методы интегрирования детерминированных систем ОДУ, а с другой, наличие случайного запаздывания и его моделирования накладывает определенные ограничения, в частности, на возможность применения встроенной функция пакета NDSolve, предназначенной для численного интегрирования дифференциальных уравнений разных типов. Это приводит к необходимости использования пользовательских процедур. В настоящей работе из соображений простоты реализации алгоритмов применяются методы Эйлера и Хойна (= улучшенный метод Эйлера) [32] для

расчетов с малым постоянным шагом интегрирования. Вследствие отсутствия прямого вхождения в модели случайных процессов, модификации указанных методов для численного решения СОДУ не применяются. Вопросы качества получаемых реализаций случайных запаздываний и допустимости неучета их стохастичности на настоящем этапе исследований не рассматривались, так как цель данной работы - продемонстрировать соответствующие инструменты пакета Mathematica в действии.

Первая из рассмотренных в этом разделе систем описывается нелинейным уравнением типа Ван дер Поля-Дюффинга с гармоническим возмущением:

Х ( t ) +2 а [ X ² ( t ) - 1 ] X ( t ) + ш 2 X ( t )+

+ вХ3(t — Y(t)) = A cos (2nYt), t> 0, X(t)= c 1, X(t)= c2, t G [10, 0], где а. ш. в- A- Y- c 1- c2 ^ постоянные. В этом случае фрагмент программного кода для мо делирования будет выглядеть так:

Т = 50; h = 0.001; nt = 50000;

t0=-4; ntau=4000; nnn=nt+ntau;

alpha = 0.1; wO = 2.5; beta = 3/8;

A = 0.305; gamma = 0.05;

xxlEs_] := 1; xx2Es_] := 0.1;

xxx = Table[0, 0, nt + ntau + 1];

ttt = Table[tO + k h, k,0,nt + ntau]; For[ k=l, k<=ntau+l, k++, tt=ttt[[k]]; xxx[[k]] = xxl[tt], xx2[tt] ];

q3 = TransformedProcess[2 +

• 1.9    Sin [3 t + 2 w Et]] , w ~ WienerProcess[ ], t];

Q3 = Interpolation[RandomFunction [q3, 0, T, 0.001]];

rhs[tx_, yyl_, yy2_] := Block[, yyl[[2]], -2 alpha (yyl[[l]]"2 - 1) yyl[[2]] - w0"2 yyl[[l]] - beta yy2[[l]]~3 + A Cos [2 Pi gamma tx] ];

euler[] := BlockEffl, ff2, yy, ffl = rhsEtttEEk]],xxxEEk]],xxxEEk-m]]]; xxxEEk]] + h ffl ];

ForE k=ntau+l, k<=nt+ntau, k++, m = RoundE Q3EtttEEk]]]/h ];

xxx E Ek + 1]] = eulerE] ]

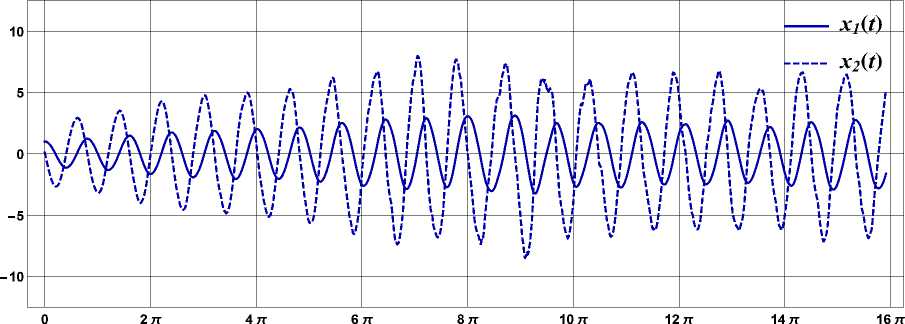
Рис. 3

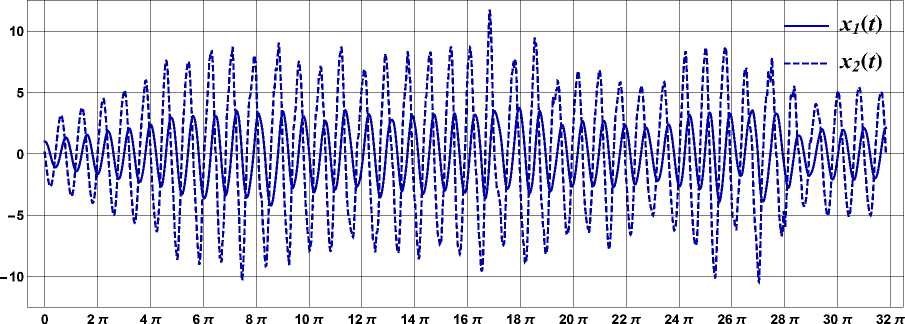
Рис. 4

Здесь случайное запаздывание, как и в предыдущем разделе, формируется на основе винеровского процесса, а для численного интегрирования системы (после введения обозначений X 1( t ) = X ( t ). X 2( t ) = X ( t )) ис пользуется схема Эйлера. Графики реализаций случайных функций X i( t ) и X 2( t ) приведены на рис. 3.

Как известно, точность указанной выше схемы для детерминированных задач равна O ( h ). Поэтому использовать ее на длинных временных промежутках не эффективно из-за необходимости применения мелкого шага. Вследствие этого в следующем примере (и далее) для анализа той же системы Ван дер Поля-Дюффинга применяется схема Хойна. Случайное запаздывание, как и в предыдущем примере, формируется на основе винеровского процесса, а для моделирования применяется следующий фрагмент программного кода (показаны только отличия от предыдущего фрагмента):

Т=100; h=0.001; nt=100000; • • • q4 = TransformedProcess[2 +

• 1.9    Sin [3 t + 2 w[t]] , w ~ WienerProcess[ ] , t] ;

Q4 = Interpolation[RandomFunction

[q4, 0, T, 0.001]];

heun[] := Block[ffl, ff2, yy, ffl = rhs[ttt[[k]],xxx[[k]],xxx[[k-m]]]; yy = xxx[[k]] + h ffl;

ff2 = rhs[ttt[[k+1]],yy,xxx[[k-m+1]]];

xxx[[k]] + h/2 (ffl + ff2) ];

For[ k = ntau + 1, k <= nnn, k++, m = Round[ Q4[ttt[[k]]]/h];

xxx [[k + 1]] = heun[] ];

Графики реализаций случайных функций X i( t ) и X 2( t ) приведены на рис. 4.

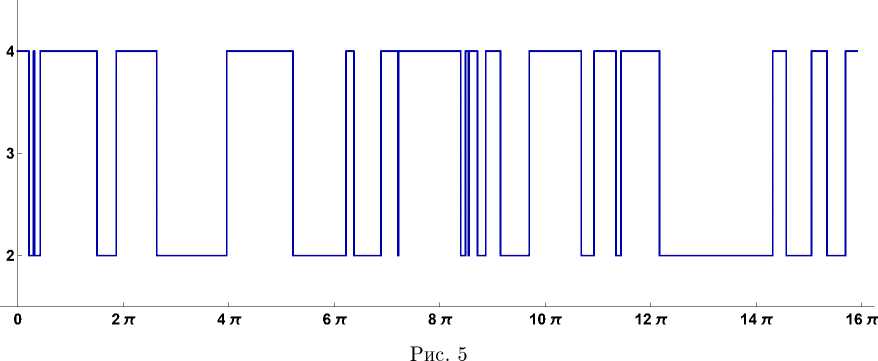
Теперь рассмотрим варианты формирования случайных запаздываний на основе использования случайных процессов с дискретным множеством состояний и непрерывным временем. В качестве таких процессов были выбраны телеграфный (ТГП) и про-

-4

-2

2π

4π

6π

8π

10π

12π

14π

16π

Рис.

стейший пуассоновский (ППП) процессы, а также цепь Маркова с тремя состояниями (ЦМЗ). Пример реализации первого из этих процессов приведен на рис. 5.

В процессе расчетов параметры процессов выбирались так, чтобы для ТГМ запаздывание принимало значения 2 и 4, а для ППП и ЦМЗ - 1, 2 и 3. Для этого применялся следующий фрагмент программного кода (показаны только отличия от предыдущего фрагмента в этом разделе):

Т=50; h=0.001; nt=50000;

• • • •

q5 = TelegraphProcess[2/3];

QQ = 3+RandomFunction[q5,0,T,h] ;

Q5 = Interpolation[QQ["Path"] ,

Interpolationorder -> 0];

q6 = TransformedProcess[1+Mod[p[t] ,3] , p ~ PoissonProcess[3/4], t] ;

• Q6 = Interpolation[

RandomFunction[q6, 0, T, h], Interpolationorder -> 0];

q7 = ContinuousMarkovProcess[1,0,0,

• -2,1/2,3/2,1/2,-1,1/2,1/2,1,-3/2] ;

• Q7 = Interpolation[

RandomFunction[q7, 0, T] , Interpolationorder -> 0] ; • • •

For[ k = ntau + 1, k <= nnn, k++, m = Round[ Q5 [ttt [ [k] ] ]/h] ;

xxx [[k + 1]] = heun[] ];

For[ k = ntau + 1, k <= nnn, k++, m = Round[ Q6 [ttt [ [k] ] ]/h] ;

xxx [[k + 1]] = heun[] ];

For[ k = ntau + 1, k <= nnn, k++, m = Round[ Q7[ttt[ [k]]]/h];

xxx[[k + 1]] = heun[] ];

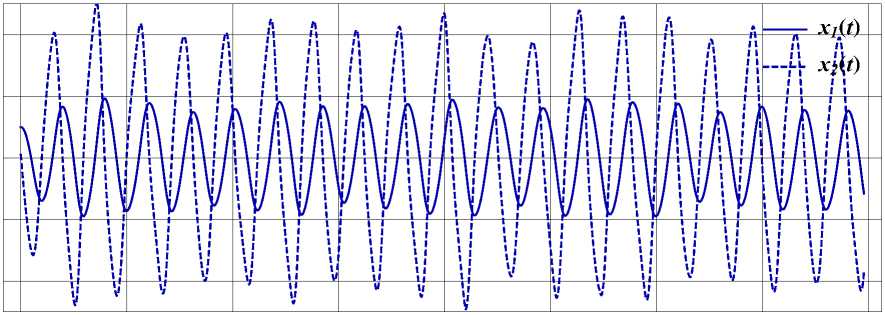
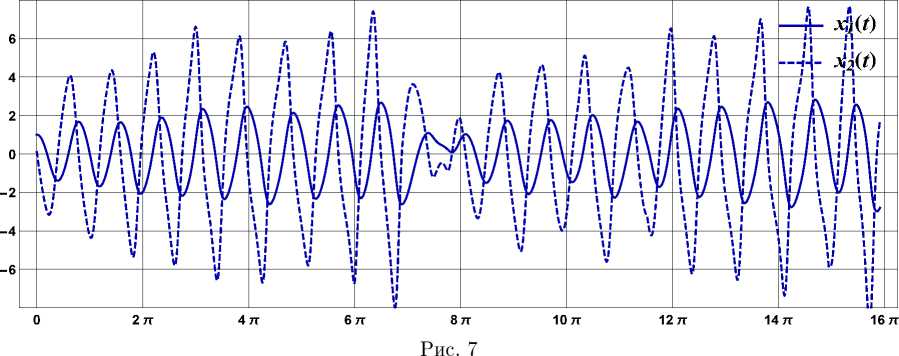
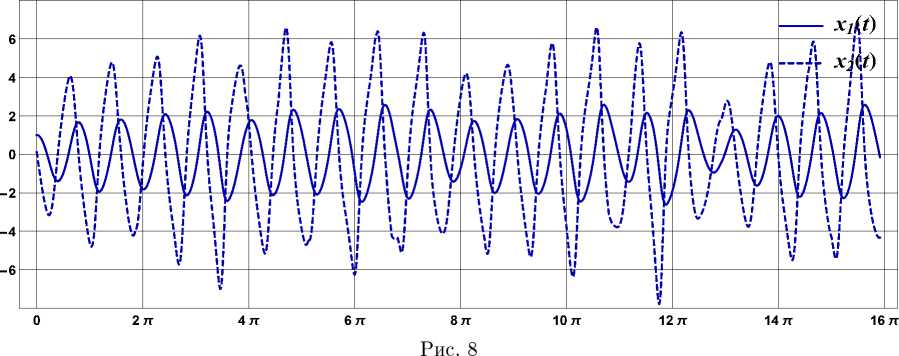
Результаты расчетов для запаздываний как функций ТГР, ППП и ЦМЗ отображены на рис. 6-8, где показано поведение реализаций случайных функций X i( t ) и X 2( t ).

Заключение

В работе были представлены некоторые результаты моделирования устойчивых почти регулярных переходных режимов в уравнении Ван дер Поля-Дюффинга с различными типами случайного запаздывания,

полученные с использованием стандартных средств описания стохастических процессов в среде пакета Mathematica. Последующая работа в данном направлении позволит проанализировать хаотические режимы, возбуждаемые в подобных системах, в т.ч. в присутствии случайных внешних и/или параметрических шумов.