Численное моделирование конвективного тепломассопереноса в сферических координатах

Авторами статьи в работе [1] была решена задача построения дискретного аналога для уравнения конвекции и диффузии в цилиндрических координатах на основе метода контрольного объема. С учетом того, что многие прикладные задачи требуют для численного решения использования криволинейных сеток, представляется целесообразным получение расчетных формул для коэффициентов дискретного аналога обобщенного дифференциального уравнения с использованием аппроксимации профилей функций между узлами сетки в сферических координатах, как это было сделано ранее для цилиндрической системы координат.

1.    Математическая модель конвективного тепломассопереноса

Математическая модель конвективного тепломассопереноса в вязкой несжимаемой жидкости определяется системой дифференциальных уравнений, полученных на основе уравнений гидродинамики, тепло- и массообмена (см., например, [2]):

ди                                    1

р ( dt + (и • V )u 1 = —V p + n V ² u + з n V • ( V • и) + рд,

|р + V. (рс) = 0,

/дТ ср ——+ и • VT = AV T.

∂t

Здесь (1) – уравнение Навье – Стокса для несжимаемой жидкости, (2) – уравнение неразрывности, (3) – уравнение теплопереноса (уравнение массопереноса имеет вид, аналогичный уравнению (3), с заменой температуры T на массовую концентрацию химической компоненты). Дифференциальные уравнения (1) – (3) описывают процессы переноса количества движения, массы и энергии. Использованы обозначения: и - скорость (векторная величина), p - давление, T - температура, р - плотность, П - динамическая вязкость, А - теплопроводность, с - удельная теплоемкость, g -напряженность гравитационного поля, t – время.

Систему уравнений для компонент вектора скорости получим, решая совместно (1), (2):

∂                    ∂p

777⁽р^ui^{) + V} • ⁽P^uui⁾ = - я--^{+ V} • ⁽n ^{V u}i) + B i + V i ,

∂t                       ∂xi где ui - i-я компонента вектора скорости (i = 1, 2, 3), Bi - составляющая объемной силы (приложенной к единице объема), Vi – дополнительные диссипативные члены.

Сравнивая (3) и (4), заметим, что u i и T подчиняются обобщенному закону сохранения, который описывается дифференциальным уравнением для обобщенной переменной Ф :

— (рФ) + V • (риФ) = V • (Г V Ф) + Ф,

где Ф - так называемый « источниковый член » (обычно представляется в линеаризованном виде, как линейная функция Ф). Физический смысл Ф и Г зависит от того, какую именно величину обозначает переменная Ф. Коэффициент Г играет роль коэффициента диффузии для уравнения переноса массовой концентрации химической компоненты, коэффициента теплопроводности для уравнения тепловой конвекции, коэффициента динамической или кинематической вязкости для уравнения движения жидкости. Источниковый член Ф может включать диссипативные и объемные компоненты, которые не учитываются конвективным и диффузионным членами уравнения (5).

Для дискретизации дифференциального уравнения (5) используем метод контрольного объема. Суть метода и его достоинства обсуждаются в книгах [3 — 5], а в работах [6, 7] приведены примеры его использования.

2.    Интегральные балансы для граней контрольного объема

Преобразуем уравнение (5) с учетом (2) к виду:

д Ф           _ _____ .

р— + ри • V Ф = V • (Г V Ф) + Ф.

Запишем это уравнение в сферических координатах (r, θ, ϕ) (см. [8, 9]):

∂Φ      ∂Φ      1 ∂Φ        1 ∂Φ

^ρ∂t ^{+ρu r} ∂r^{+ρu θ} r∂θ^{+ρu ϕ} rsinθ∂ϕ⁼

_1 А ( 2 Г дФ ^{А      1 9 (} i _{6 г} ⁹ Ф ^{А      1     9 (} _Г ⁸ Ф А *

r ² ∂r       ∂r     r ² sin θ ∂θ ∂θ     r ² sin ² θ ∂ϕ ∂ϕ ^.

В это уравнение входят соответствующие компоненты вектора скорости u ¯ = u _r , u _θ , u _ϕ . Уравнение неразрывности в сферических координатах имеет вид:

+ 4   (r ² Pur) ⁺  1"fl in (sin ⁶Pu⁶ ) ⁺        ТТ ^u ^ ) = 0'          ⁽⁷⁾

∂t r ² ∂r          r sin θ ∂θ             r sin θ ∂ϕ

Преобразуем уравнения (6), (7), умножая их левые и правые части на r ² и r ² Φ соответственно:

∂Φ ∂Φ sin θ ∂Φ r ∂Φ

+ ρuϕ       = sin θ ∂ϕ

Т (г £ А + r2 *

sin ² θ ∂ϕ    ∂ϕ

r ² ρ_∂t + r ² ρu r _∂r + r ² ρu θ_{sin θ∂θ}

= у (r2 г ^Ф А ^ (sin ⁶ г Ф а +

∂r ∂r sin θ ∂θ∂θ

и г2ф д+Ф dr (r2pur)+Ф sin» ^(sin 6 pu«)+Ф sine dd=0.

Преобразуем уравнение конвекции и диффузии (8), используя уравнение неразрывности (9):

r ² sin 6 77- (p Ф) +    (r ² sin 6 pu r Ф) +    (r sin 6 pu_e Ф) + 77- (три_ф Ф) =

∂t ∂r               ∂θ∂ϕ

=   (r ² sin 6 Г   А + In (sin 6 Г ^дФ А +    (-ДлГ А + r ² * sin 6.

∂r          ∂r ∂θ        ∂θ ∂ϕ sin θ ∂ϕ

Расчетную область разобьем на множество непересекающихся контрольных объемов, в каждом из которых будет содержаться только одна узловая точка. Разбиение проводим координатными поверхностями (см. [9]): x ² + y ² + z ² = r ² (сферами, r = const, r >  0), x ² + y ² — z ² tg ² 6 = 0 (круглыми конусами, 6 = const, 0 <  6 <  n, 6 = n/2), y = xtgd (полуплоскостями, d = const, 0 <  d < 2n, d = n/2, d = 3n/2).

Рассмотрим типичный контрольный объем V с узловой точкой P (рис. 1). Обозначим через n и s верхнюю ( ≪ северную ≫ ) и нижнюю ( ≪ южную ≫ ) грани контрольного объема, через w и e – левую ( ≪ западную ≫ ) и правую ( ≪ восточную ≫ ) грани, через t и b – ≪ внешнюю ≫ (большего радиуса) и ≪ внутреннюю ≫ (меньшего радиуса) грани. ≪ Северная ≫ и ≪ южная ≫ грани представляют собой части конических поверхностей, ≪ западная ≫ и ≪ восточная ≫ грани – части полуплоскостей, ≪ внешняя ≫ и ≪ внутрен-няя ≫ грани – части сферических поверхностей. Для удобства представления формул используем такие же обозначения в записи соответствующих этим граням значений переменных. Таким образом, через θ _s обозначим значение переменной θ на ≪ юж-ной ≫ грани, а через θ _n – значение этой переменной на ≪ северной ≫ грани. Тогда для данного контрольного объема выполнено условие 6_n <  6 <  6 s . Аналогичным образом вводятся обозначения для граничных значений переменных d и r: d e <  d <  d w ,

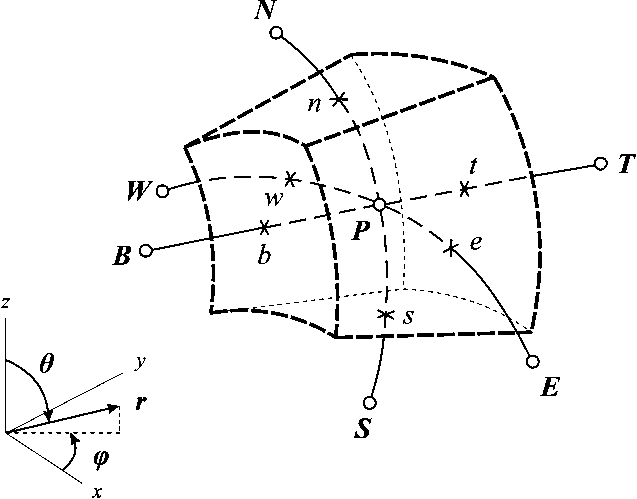
Рис. 1. Контрольный объем V с узловой точкой P

r b ≤ r ≤ r _t . Следовательно, интегрирование по рассматриваемому контрольному объему – это интегрирование по области

V = { (r, 9yp^ I Г ь <  r <  r t , 6 n <  9 <  9 s , y e <  y <  ^ w } .

Уравнение (10) проинтегрируем по указанному контрольному объему V и по временному промежутку [t ₀ , t ₀ + At].

.Ш ^r 2 ^{s,n 6}

V

t 0 +∆ t

∂ dt (рФ) dt dr d6 dy + t0

t 0 +∆ t θ s ϕ w      r t

/ //[/dr(r2sin6purф- t0 θnϕe      rb

— r ² sin 6 Г I dr d6 dy dt + ∂r

- sin 9 ^Г gp⁶]

dr dy dt +

t 0 +∆ t r t θ s

t 0 +∆ t r t ϕ w     θ _s

/ //  / ^(r sin 6pUg Ф - t0 rbϕe     θn

ϕ w

t 0

t 0 +∆ t

I П / dy ^Ф

r b θ n

ϕ e

Г d Ф sin 6 dy

^ dy drd6dt =

= 1 JJJr² sin 6 ^ dr d6 dy dt.

t 0

V

Аналогично интегрируем уравнение неразрывности (7):

r ² sin 6

V

t0+∆t r dp

∂t t0

t 0 +∆ t r t ϕ w     θ _s

t 0 +∆ t θ s ϕ w     r t

dt dr d6 dy + J JI  j — (r ² sin 6 pu r ) dr I d6 dy dt +

t 0    θ n ϕ e

r b

t 0 +∆ t r t θ s

ϕ w

+/ Jj j_dL(r sin 6 pu g ) d6 I dr dy dt + j     \ /

— (rpu^ ) dy drd6dt = 0.

t 0    r b ϕ e      θ n

t 0    r b θ n     ϕ e

Размеры контрольного объема V определяются значениями Ar = r t — r b , Д^ = ^ w — ^ e (рис. 2) и Д9 = 9 s — 9 n (рис. 3). Пусть (5r) t - расстояние между узловыми точками P и T , а (6r) b - расстояние между P и B . По такому же принципу обозначим расстояния между другими парами узлов: (5^)_w - между P и W , (5^) e - между P и E , (50) n - между P и N , (59) s - между P и S . Узловая точка P характеризуется координатами r _P , θ _P и ϕ _P .

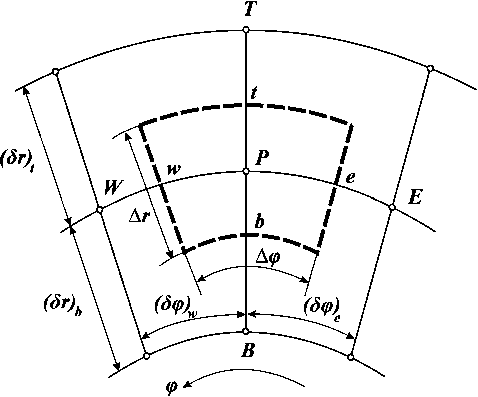
Рис. 2. Проекция сечения контрольного объема V конусом 9 = 9 P на касательную плоскость (точка касания – узел P )

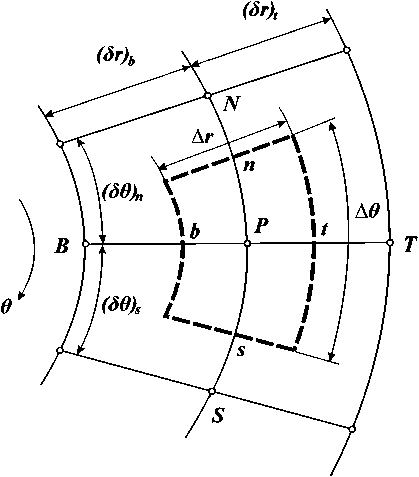
Рис. 3. Сечение контрольного объема V полуплоскостью ^ = ^_Р

Введем понятия суммарных потоков, направленных вдоль осей координат и складывающихся из конвективных и диффузионных составляющих:

J r = r ² sin 9 pu r Ф — r ² sin 9 Г ^—, J₆ = r sin 9 pu g Ф — sin 9 Г d—. ,

Г дФ

J - = ^—р" ^ ^{ф —} swi n'

Тогда с учетом формул (13) уравнение (11) примет вид:

Ш r^{2 sin}

V

∂J _ϕ ∂ϕ

t 0 +∆ t

J dt ■^?;' t 0

t0 +∆t d ■■ +/ [yyy( p + a.

)-i        tg + At dr d6 dy dt = j  J J J t0        V

r ² sin 6 Ф dr d6 dy dt.

t 0

Пусть J t – значение потока J r на грани t , а J b – значение J r на грани b . Также обозначим через J s и J n значения J θ на гранях s и n , а через J w и J e – значения J ϕ на гранях w и e. Значения переменной Ф в момент времени t o + At (новые значения на текущем временном шаге) в узловых точках P , T , B , S , N , W , E обозначим Ф _р , Ф _т , Ф _в , Ф s , Ф _N , Ф w , Ф _Е . Значение Ф в момент времени t ₀ в узле P обозначим Ф р . Пусть р_Р и р р - значения переменной р в узле P в моменты времени t ₀ + At и t 0 . При аппроксимации интегралов дискретными аналогами будем использовать неявную схему: на временном шаге t o < t <  t o + At полагаем значения Ф и р равными новым значениям Ф р и р р . Кроме того, согласно применяемому методу считаем, что значения переменных Ф и р во всем контрольном объеме V равны их значениям в узловой точке P . При указанных допущениях уравнение (14) аппроксимируется следующим дискретным аналогом:

(р р ^Ф Р ^— р р ^Ф р ) "At + ^(J t ^— J b ) ^A6Ay + ^(J s ^{— J} n ) ^ArAy + ^(J w

- J _e ) Ar A6 = ФAV, (15)

где Ф - среднее по контрольному объему значение

t o . A t , A V

111 r² sin 6 dr d6 dy =

V

2 z 9

3 (r² + r t r b + rb²)

Ф sin

в момент времени ' . ^V ArAy.

2        2

Отметим,

AV = ⁽2г р

rt . rb что при Тр  =  2  и

— 6 (Ar) ² ) sin 6_р sin A6 Ar Ay.

6 _s . 6 _n

6 p =  ------ р          2

выполнено равенство

Введем обозначения:

F_r = r ² sin бри, F g = r sin 6 ри д , F ^ = rрu_ф.                 (16)

При этом F t и F b – значения F r на гранях t и b , F s и F n – значения F θ на гранях s и n , F w и F e – значения F ϕ на гранях w и e . Учитывая (16), составим дискретный аналог уравнения (12):

(р р — р р ) AV ⁺ (F t — ^F b )A6Ay + (F . — F nW Ay + (F W — F) ArA6 = 0.

Из (15) и (17) получим

( ^ф р — ^ф р ) ^^ At--. ^(J t ^{— F} t ^ф р ^)A6Ay — ^(J b — ^F b ^ф р ^)A6Ay+

+ ^(J s ^{— F} s ^Ф P ^)ArAy ^{— (J} n ^{— F} n ^Ф р ^)ArAy + ^(J w ^— F w ^Ф р ^{)ArA6 —       (}^)

— (J _e — F e Ф _р )ArA6 = ФAV.

3.    Точные решения уравнений сохранения

Следуя [9], будем именовать координаты r, θ, ϕ полярным радиусом, широтой и долготой. Для получения лучших аппроксимаций профилей обобщенной переменной в различных направлениях найдем точные решения уравнений сохранения отдельно по каждой координате.

• I.    Рассмотрим установившееся течение в направлении возрастания полярного радиуса r (θ = const, ϕ = const, R ₀ ≤ r ≤ R ₁ ):

( r ² sin 9 pu r Ф — r ² sin 9 Г^ ) = 0,-77- (r ² sin 9 pu r ) = 0.

∂r                        ∂r ∂r

Упростим систему уравнений (19), учитывая θ = const:

^∂ r ² ρu r Φ - r ² Γ ^{∂ Φ} = 0 , ∂r              ∂r

( r ² pu r ) = 0.

∂r

Обозначим r ² ρu _r = k = const. Рассматривая течение как одномерное, получаем уравнение относительно функции одной переменной Φ = Φ( r ) (Φ ^′ _θ = Φ ^′ _ϕ = 0). В предположении Γ = const задача сводится к решению краевой задачи для обыкновенного дифференциального уравнения в области R ₀ ≤ r ≤ R ₁ (рис. 4):

k Φ ^′ r - 2 r ΓΦ ^′ r - r ² ΓΦ ^′ r ^′ r = 0 , Φ( R 0 ) = Φ 0 , Φ( R 1 ) = Φ 1 .            (20)

Задача (20) приводится к виду k-2rΓ ln Φ′r ′r= k r22ΓrΓ, Φ(R0) =Φ0, Φ(R1) =Φ1.

Последовательно интегрируя, находим общее решение дифференциального уравне- ния:

Φ( r ) = C 1 ^e

-

k/ ( r Γ)

_{r 2}    dr = C 1 ^Γ _k e ^-k/(rΓ) + C 2 .

Учитывая начальные условия, находим решение системы (19):

Φ - Φ 0

k ( r - R 0)

e r ^{r R} o   — 1

Φ 1

-

Φ 0

k ( R i - R o)

e r R o R i   _— 1

Рис. 4. Область решения одномерной задачи в направлении r

• II.    Рассмотрим установившееся течение в направлении возрастания θ (вдоль дуги M 0 M 1 , r = const, ϕ = const, θ 0 ≤ θ ≤ θ 1 , рис. 5):

(r sin 9 pu₆ Ф — sin 9 Г    ) = 0,     (r sin 9 pu₆ ) = 0.

∂θ                    ∂θ ∂θ

Граничные условия: Φ( θ ₀ ) = Φ ₀ , Φ( θ ₁ ) = Φ ₁ .

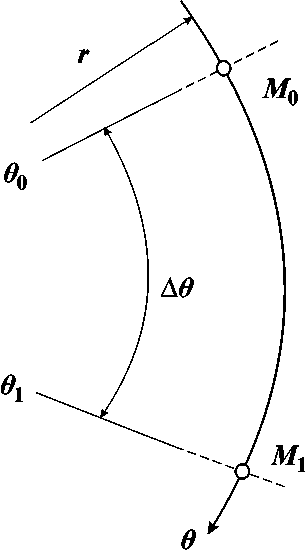
Рис. 5. Область решения одномерной задачи в направлении θ

Запишем систему уравнений (22) в виде:

∂Φ   ∂       ∂Φ rsinθρuθ∂θ-∂θ sinθΓ∂θ  =0,

r sin θ ρu θ = const.

Обозначим r sin θ ρu θ Γ ^-1 = k. В предположении, что Φ = Φ(θ), Φ ^′ _r = Φ ^′ _ϕ = 0 и Γ = const, получаем краевую задачу для обыкновенного дифференциального уравнения в области θ ₀ ≤ θ ≤ θ ₁ :

kΦ ^′ _θ - cos θ Φ ^′ _θ - sin θ Φ ^′ _θ ^′ _θ = 0,   Φ(θ 0 ) = Φ 0 ,   Φ(θ 1 ) = Φ 1 .

Аналогично задаче (20)

il-i •;=k - c^

«"=Ci/(tg 2 )* £=«/('g 2 p (- 2)=C ('g 2)

k

+ C ₂ .

Решение запишем в виде, аналогичном (21)

ф - Ф о = (tg(g/2)) ^k - (tg(^ 0 /2)) k ^ф 1 ^{- ф} о     (tg(^/2)) ^k - (tg(6 o /2)) ^k '

III. Рассмотрим установившееся течение в направлении возрастания ϕ (по дуге L ₀ L ₁ при r = const, θ = const, ϕ ₀ ≤ ϕ ≤ ϕ, рис. 6):

^ (гц!ф -      ^дФ^)=0, ^d- (rpu^, ) =0.              (25)

∂ϕ          sin ϕ ∂ϕ ∂ϕ

Граничные условия: Φ(ϕ ₀ ) = Φ ₀ , Φ(ϕ ₁ ) = Φ ₁ . Из (25) следует, что rρu _ϕ = const. Пусть rρu _ϕ sin θ Γ ^-1 = k . В предположении, что Φ = Φ(ϕ), Φ ^′ _r = Φ ^′ = 0 и Γ = const, получаем краевую задачу для обыкновенного дифференциального уравнения в области ϕ ₀ ≤ ϕ ≤ ϕ ₁ :

kΦ ^′ ϕ - Φ ^′ ϕ ^′ ϕ = 0, Φ(ϕ 0 ) = Φ 0 , Φ(ϕ 1 ) = Φ 1 .

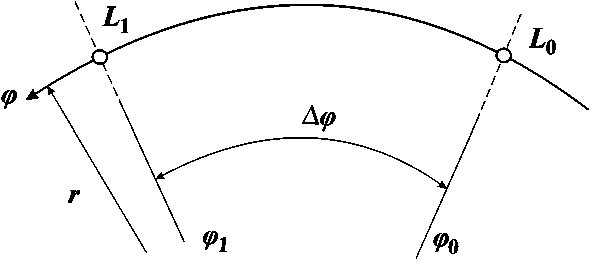
Рис. 6. Область решения одномерной задачи в направлении ϕ

Решая систему (26), найдем:

Ф - Ф _о     e ^k ^⁰ ) — 1

Ф 1 _— Ф 0     _e ^k( ^ 1 ^- ^ 0 ) _— 1"

4.    Физический смысл точных решений

Итак, точные решения в случае одномерных течений по каждой из координат задаются соотношениями (21), (24) и (27). Входящий в каждую из формул коэффициент k зависит от выбора координаты. Поскольку ранее (см. [1]) авторами уже было проведено исследование физического смысла точных решений для случая цилиндрических координат, следует привести лишь общую схему решения данной частной задачи. Для каждого аналитического решения определим соответствующие ему числа подобия (числа Пекле, определяющие соотношение между конвективными и диффузионными членами в уравнениях (4)).

В системе (19) k = T2pur. Определим число Пекле в этом случае равенством р k(R1 — Ro)   r2pur AR r = ГН1 Ro = FRi Ro ’ где AR = R1 — Ro - характерный размер. В этом случае уравнение (21) принимает вид:

Ф = Ф о + (Ф 1 — Ф о ) e^ ^{Г) —}- ¹ , f (r) = AZ- R⁰^,           (28)

ePr — 1             r AR где f (r) - безразмерная нелинейная функция координаты r, причем 0 < f (r) < 1 при R0 ≤ r ≤ R1.

В системе (25) k = rpu ^ sin 9 Г ^-1 , и число Пекле определяется равенством

_D              , rpu_v sin ⁹

Pv = k(^i — Vo) =---Г где Ay = V1 — V0 — характерный размер. В этом случае уравнение (27) принимает вид:

Ф = Фо + (Ф1 — Фо) e Р"р ^^ — 1, f (v)= (V — Vo),(29)

\        / ePv — 1A^

где f (v) — линейная функция переменной v (безразмерная координата), 0 <  f (v) <  1 при ϕ 0 ≤ ϕ ≤ ϕ 1 .

Зададим число Пекле в системе (22) соотношением

P g = k In

tg(9 i /2)

tg⁽⁹ o ^/2)

rpu₆ sin 9   tg(9 i /2)

Г n tg(9 o /2)'

Уравнение (24) в этом случае принимает вид:

e P e f (9) - 1

^ф = ^ф ₀ + (^ф 1 ^{— ф}₀) e p _e - —

₌ ^lntg^{(0/2) —} lntg(^ 0 ^/2)

^{f (} )   lntg(0 i /2) - lntg(^ 0 /2)’

где f (0) - безразмерная нелинейная функция переменной 9 такая, что при 6₀ <  О <  0 1 ее значения определяются неравенством 0 <  f (0) <  1.

Поскольку точные решения во всех трех случаях можно представить обобщенным уравнением

^Ф(£) = ^ф о ⁺ (^Ф 1 ^{— ф} о )

e ^{Pf (} 5 ) — 1 e ^p — 1

где ξ – обобщенная координата, то и поведение точных решений в зависимости от значений числа Пекле P будет аналогичным. Теперь к последнему уравнению применимы результаты, полученные в [1]. В пределе при P ^ 0 (в случае « чистой » диффузии) зависимость Ф(£) от £ определяется функцией f (£). Чем больше P ^ 1, тем больше влияние Ф ₀ на грани контрольного объема. При P ^ — 1 чем больше | Р | , тем больше влияние Ф 1 . В случае, если £ = 0 и значение | Р | велико, то на грани контрольного объема, расположенной посередине между узлами, производная Ф ^ близка к нулю, то есть диффузия почти отсутствует.

5.    Дискретный аналог для обобщенного дифференциального уравнения

Используем полученные аналитические решения для построения дискретного аналога обобщенного дифференциального уравнения (18).

• I.    Найдем приближения для потоков J t и J b на ≪ внешней ≫ и ≪ внутренней ≫ гранях контрольного объема. В качестве профиля между узлами P и T возьмем функцию, определяемую равенством (28), заменив Ф ₀ на Ф _р , а Ф 1 на Ф _т . Примем R ₀ = R_P , AR = (5r )_t, R 1 = R T = R _P + (§r )_t • Тогда

Ф = Фр +Ф^ фр ;. f (r) — 1) , Pt = r            t, Ft = r2(pur)t sin 0, ePt — 1                        Г tRPRT

, x   (r - RP)RT f (r) =—, Rp < r < Rt, r δr t где rt – значение полярного радиуса на ≪внешней≫ грани t контрольного объема.

Найдем выражение для потока Jt и покажем, что расположение границы раздела между узлами P и T не существенно. Заметим, что Pt = Ft       t. Следова-

F _t R _P R T sin 0 тельно,

J = FФр + F Ф т   Ф р e P t f ( r t ) — t     t P     t eP t - 1 Фт — ФР = F t Ф р — F t^--p- e P t - 1

F ф т — ф р — F ф р — ф р e p t f (r t ) = t e P t — 1       t e P t — 1 , Фр — Ф т 1                     ( ) = F t Ф р + eP, — 1   ■

Поскольку f (r _t ) в (31) не входит, то значение J_t не зависит от расположения границы раздела между узлами.

Аналогично, на ≪ внутренней ≫ грани контрольного объема

J b = F b

Φ B - Φ P

^{Φ B +} e ^P b - 1

где F b = r _t ² ρu r _t sin θ , P b узле B.

r _b ² ρu r _b δr _b

^Γ b ^R P ^R T    ^,

Φ _B – значение обобщенной переменной в

• II.    Найдем приближения для потоков J s и J n на ≪ южной ≫ и ≪ северной ≫ гранях контрольного объема.

В качестве профиля между узлами P и S используем функцию (30), заменив Φ0 на ΦP , Φ1 на ΦS, θ0 на θP, θ1 на θS. Положим ∆θ = θS - θP = δθ s . Тогда ф = Фр + 5S^ (ePsfw - 1) , ePs - 1

ln tg(θ/2) - ln tg(θ P /2)

^f(θ)   lntg(θ S /2) - lntg(θ P /2)^,

где θP ≤ θ ≤ θS = θP + δθ s . На ≪южной≫ грани s контрольного объема rs – значение полярного радиуса, θs – значение широты, rs ρuθ sin θ         θS        θP

P s = —г— s (lntg^ ^— lntgyj^, F s = r s ( pu ^e sin ^s -      ⁽³³⁾

Поток J s на ≪ южной ≫ грани можно представить, с учетом равенств (33), в виде:

^Φ S ^{- Φ} P P s f ( θ s )       ^Φ S ^{- Φ} P ^Φ S ^{- Φ} P P s f ( θ s )

J s = F s Φ P + F s _{e P s - 1} e        F s _{e P s - 1}    F s _{e P s - 1} e =

= F s Φ P

— F

s

Φ S - Φ P

_e P s

- 1

= F s

Φ P +

Φ P - Φ S

_e P s

- 1

I

Значение J _s не зависит от расположения границы раздела между узлами, так как в выражение (34) f (θ _s ) не входит.

Аналогично, на ≪ северной ≫ грани n контрольного объема

J n = F n

Φ N +

Φ _N - Φ _P

e ^{P n} - 1

sin θ n n обобщенной переменной в узле N .

III. Найдем приближения для потоков J _w и J _e на ≪ западной ≫ и ≪ восточной ≫ гранях контрольного объема.

Для аппроксимации профиля между узлами P и W используем функцию (29), заменяя Φ 0 и Φ 1 на Φ P и Φ W , ϕ 0 и ϕ 1 на ϕ P и ϕ W , ∆ϕ на δϕ _w . Тогда для значений ϕ _P ≤ ϕ ≤ ϕ _W

где F n = r n ρu θ sin θ _n , P n

r n ρu θ

Γ

ln tg ₂ ^N - ln tg ₂ ^P , Φ _N – значение

ΦW - ΦP Φ = ΦP + ePw - 1

⁽ _e P w f (V) _—

f(ϕ) =

ϕ - ϕ P

^{( 5}^ ⁾ w ^,

δϕ _w = ϕ W - ϕ P .

На ≪ западной ≫ грани контрольного объема F w = r w ρu ϕ _w , P w

r w ρu ϕ _w sin θ

ϕ w – угол до грани w от узла P . Поток J w можно представить в виде

Γ w

δϕ _w ,

J w = F w [ф р + ^? W     ^ф •■    f (» " ⁾ - 1)1

e ^{P w} - 1

г w sin θ

Φ _W - Φ _P

e ^{P w} - 1

e P w f ⁽ V w ) ^P w

(Mw

= F w Φ P + F w

^ w_ I P e P w f (v w )

e ^{P w} - 1

- F

w

Φ W - Φ P

e ^{P w} - 1

w

^W—^P ePw f (Vw ) = ePw - 1

= F w Φ P

w

Φ W - Φ P

e ^{P w} - 1

= F = _w

Φ P +

Φ P - Φ W

e ^{P w} - 1

I

Заметим, что J w также не зависит от расположения границы раздела между узлами.

Аналогично, на ≪ восточной ≫ грани e контрольного объема

^J e = F [^Ф Е + ⁵I^ ] -                  (37)

re ρuϕ sin θ где Fe = re ρuϕ e , Pe = e δϕ e , ΦE – значение Φ в узле E.

Γ _e

Подставим полученные выражения суммарных потоков (31), (32), (34) – (37) на гранях контрольного объема в уравнение (18). Окончательный вид дискретного аналога:

a P Φ P = a T Φ T + a B Φ B + a S Φ S + a N Φ N + a W Φ W + a E Φ E + b,        (38)

где ар = ар + ат + aв + as + aN + aw + aE — Фр △V,

	F t	P b	F s
a T =	∆ θ ∆ ϕ, a B e P t - 1	= e   F b ∆ θ ∆ ϕ, e P b - 1	a S =       ∆ r ∆ ϕ, e P s - 1
	e P n	F	e P e
a N =	F n ∆ r ∆ ϕ, e P n - 1	a W = w  ∆ r ∆ θ, e P w - 1	a E =        F e ∆ r ∆ θ, e P e - 1
a 0 P =	p P △ V   ь - q0 ф0 ∆ t , b = a P Φ P	+ Ψ C ∆ V.

Полученный дискретный аналог для обобщенного дифференциального уравнения может быть использован для численного моделирования конвективного тепломас-сопереноса в условиях ламинарных и турбулентных течений вязкой несжимаемой жидкости на криволинейных сетках в случае использования сферических координат. Расчетные формулы получены на основе точных решений уравнений переноса, поэтому при их использовании для расчетов повышается точность результатов, что является важным аргументом в пользу рассмотренного метода дискретизации при численном моделировании на основе уравнений Навье – Стокса.

Работа поддержана Правительством Российской Федерации (акт № 211), договора № 02.А03.21.0011.