Численное моделирование стружкообразования при лезвийном резании волоконно-армированной композитной заготовки объемного плетения. Часть 2: геометрическое и физическое моделирование

И.А. Щуров, , И. Щурова, , Г.В. Вольф,

I.A. Shchurov, , Shchurova, , Volf ,

Данная статья является продолжением выполненного ранее анализа публикаций, посвященных численному моделированию процесса резания композитных заготовок и связанному с ним набору математических моделей материалов, используемых в этих композитах. Как было показано ранее, такое численное микромоделирование резания лезвийным инструментом заготовок из волоконно-армированных композитных материалов (ВКМ) включает в себя применение моделей материалов, образующих как собственно волокна и матрицу, так и применение моделей граничного слоя матрицы, прилегающего к волокну. Выбранная в первой части статьи модель для металлического композита представляет собой общую модель Johnson–Cook (JC) как для волокон из американской марки стали 1045 [1], так и для матрицы из алюминиевого сплава 6061-T6 [2]. Данный выбор был обусловлен широким применением в численном моделировании процессов резания именно этой модели материалов, которая отличается сравнительно простым видом и поэтому дает экономичный расчет. с одной стороны, а с другой стороны, она учитывает как сами деформации, так и их скорости, а также температуры деформируемых материалов. Важным вопросом моделирования резания с применением этой модели является выбор ее параметров. Известно, что для одних и тех же марок материалов можно подобрать различные наборы коэффициентов указанной модели. Данные наборы коэффициентов приведены в различных литературных источниках. Построенные по выбранным из этих источников наборам параметров графики напряжений в зависимости от относительных деформаций и их скоростей позволил выбрать такие наборы по линиям, проходящим примерно посредине других линий. Выбор той же самой модели JC для граничного слоя волокно - матрица был обусловлен тем обстоятельством, что этот материал все же является материалом матрицы, но он у волокна имеет меньшую прочность, поскольку при начальных деформациях разрушение композита начинается с отрыва волокон от матрицы. Дальнейшее же увеличение деформаций композитной заготовки приводит к разрушению как самой матрицы, так и в последствии волокон.

После реализации первого этапа рассматриваемого исследования, на втором его этапе было выполнено решение задачи моделирования процесса лезвийного резания заготовки из композита. Здесь необходимо было разработать геометрическую микромодель данной композитной заготовки, а далее на ее основе создать физическую модель, после чего произвести само физическое моделирование процесса резания. Очевидным решением в создании геометрической модели могло бы быть использование методов аналитической геометрии, которые в настоящее время на практике реализованы в коммерческих CAD-программах. Однако переход от такой аналитической модели к численной физической модели в общем случае непредсказуем. В частности, моделирование с использованием метода конечных элементов (МКЭ) требует для заданной детали совпадения узлов ее смежных конечных элементов. Такое условие при создании регулярных сеток решается вводимыми условиями разбиения подобласти по ее границам, в частности, по ребрам. Для простых по форме поперечного сечения волокон такое разбиение не вызывает трудностей. Разбиение же сложных тел, например, матрицы, на конечные элементы производится, как правило, лишь нерегулярными сетками, что сопровождается определенными трудностями с совпадением их узлов с узлами примыкающих волокон. Преодолевая данные трудности, исследователям еще в начале 2000-х удалось создать конечно-элементные модели волоконно-армированных композитов объемного плетения [3, 4]. Сразу же появились коммерческие компьютерные программы типа WiseTex, предназначенные для создания подобных моделей [5]. Такие же программы типа TexGen развиваются и реализуются в настоящее время [6]. Однако в данных компьютерных программах требуемого описания конечными элементами граничных слоев волокно-матрица обнаружить не удалось. Кроме того, данные волокна моделируются абсолютно гладкими, что характерно для случая применения аналитической геометрии в пространстве, но не соответствует реальным шероховатым поверхностям волокон, что особенно актуально для большинства полимерных композитов. Как известно, применение МКЭ для решения задач с разрушением материала имеет и другие, органически присущие данному методу расчета недостатки, что стало причиной появления других численных, в частности, бессеточных методов расчета. Одним из таких методов для решения задач резания заготовок из гомогенных и гетерогенных материалов стал метод гидродинамики сглаженных частиц Smooth Particle Hydrodynamics (SPH), зачастую применяемый совместно с традиционным МКЭ [7]. Особенностью SPH моделирования является применение специфических подобластей разбиения -частиц с одинаковыми по всем направлениям размерами, которые не меняются для всех частиц. Эта особенность SPH моделей сходна с другим численным методом - методом геометрического моделирования на базе воксельного подхода [8].

Воксельное моделирование по принципу растровых моделей позволяет описывать тела и их поверхности любой степени сложности, например, даже лица людей [9], а также такие специфические черты, как шероховатость этих поверхностей. Одним из вариантов получения воксельной модели волоконно-армированного композита объемного плетения является расчет ее сетки из аналитической модели [10]. Далее на этой основе возможно решение, например, тепловой или смешанной задачи. Однако конкретных результатов таких расчетов в анализируемом источнике

Вольф Г.В.

найти не удалось [10]. Методика получения воксельной сетки на основе CAD-моделей технологического оборудования была ранее опубликована автором данной статьи1 в 22-м томе этого же журнала в 2022 г. Другим примером расчета воксельной сети на основе уравнений, описывающих твердотельную модель конкретного объекта (в данном случае спирального сверла), является публикация автора2 в 20-м томе этого же журнала в 2020 г. Наконец, можно отметить и опыт расчета воксельной модели волоконно-армированной детали в еще более ранней публикации на основе трехмерного растрового и растрово-векторного редактора [11]. Причем в последнем случае моделировались не только волокна и граничные слои матрицы, но и загущение и разряжение волокон в зависимости от напряжений в данной области детали при ее рабочем нагружении. Одним из широко распространенных приемов создания численных моделей композитных материалов является применение «представительных объемных элементов» (ПОВ) как для волоконно-армированных [12, 13], так и для дисперсно-армированных [14] композитов. Такой подход снижает трудоемкость в разработке структуры композита внутри ПОВ. Однако это не снижает общей размерности численной модели и усложняет построение общей модели детали при соединении данных ПОВ в общую структуру, в особенности ограниченную сложными по форме поверхностями. Таким образом, имеется множество исследований геометрического моделирования деталей из ВКМ, включая как аналитические модели, так и численные модели на основе воксель-ного подхода, при этом последний реализуется на основе тех же аналитических CAD-моделей, моделей на основе уникальных зависимостей, характеризующих моделируемое тело, или путем применения растровых и растрово-векторных редакторов. Во всех этих публикациях не удалось обнаружить итоговые зависимости и построенные по ним геометрические или связанные с ними физические численные модели на основе воксельного и SPH-подходов. Следовательно, необходимо получить новое решение для автоматизированного получения воксельных геометрических и связанных с ними SPH физических моделей заготовок из ВКМ объемного плетения, в которых бы волокна и граничные слои описывались с неровностями, характерными для данных материалов.

В связи с этим, как было отмечено в первой части статьи, целью данного исследования на первом этапе является выявление на основе анализа имеющихся публикаций параметров моделей материалов и на втором этапе – численное моделирование стружкообразования при резании лезвийным инструментом заготовок из волоконно-армированных композитных материалов объемного плетения. При этом последнее включает в себя и разработку численной геометрической микромодели композитной структуры.

Для достижения второго этапа из указанной цели необходимо было произвести анализ доступной литературы, посвященной воксельному и SPH-моделированию волоконно-армированных композитов. Применение методов расчета напряжений в композитах с использованием итерационных дискретных методов получило отражение еще в работах 1990-х годов [15, 16]. Развитие этих методов и методов воксельной дискретизации расчетной области на подобласти происходит параллельно. Примеры расчета воксельных сеток для дисперсно-армированных композитов, по-видимому, были опережающими. Воксели композитных структур с частицами и порами преобразовывались в объемные элементы для физических расчетов и далее реализовывались в расчетах напряжений и деформаций [17]. Подобные модели разрабатывались и одним из авторов данной публикации, что нашло отражение в его работах, напечатанных в изданиях базы данных SCOPUS в период с 2016 по 2022 г. Такие модели включали в себя и использование сканирования реальных частичек наполнителя, и последующее использование полученных их графических образов в расчетах стружкообразования композитных заготовок. Подобные модели продолжают разрабатываться и другими исследователями [18], которым удалось получить описание достаточно сложных структур, однако подробных зависимостей для описания данных геометрических моделей в статьях обнаружить не удалось. Особо следует отметить работу с использованием сферических частичек наполнителя композита с граничными слоями матрицы некото- рой толщины [19]. В цитируемой работе приведены результаты исследований по влиянию размеров вокселей на точность расчетов. Показано, что при уменьшении размеров вокселей в 12 раз ошибки вычислений уменьшаются на порядок. Одновременно с этим в своих выводах автор отмечает, что оценка нормальных напряжений на границе раздела наполнитель-матрица на основе быстрого преобразования Фурье (FFT) невозможна без использования промежуточного вокселя. Данные выводы можно принять к сведению, но с одним уточнением: сферические наполнители в дисперсно-армированных композитах практически не применяются. Форма таких частиц, как правило, сложная и имеет хаотичную структуру, что и показано в упомянутой выше статье одного из авторов текущей публикации в 2019 г. в журнале Lecture Notes in Mechanical Engineering, посвященной использованию сканирования частичек для описания композита. Учитывая сложность формы частичек наполнителя, целесообразность приема описания граничного слоя матрица - наполнитель в виде полой тонкостенной сферы вызывает сомнения. Вопросу учета интерфейсов (границ) волокно - матрица в процессах разрушения композита посвящена и другая известная работа [20]. В отличие от предыдущей, здесь рассматриваются волокна цилиндрической формы. Отличием является и то обстоятельство, что интерфейсный слой некоторой заданной толщины здесь не рассматривается вообще. Вместо этого граница волокно - матрица принимается как некоторая поверхность с заданными характеристиками разрушения. Критика такого подхода встречается в вышеприведенных и других работах. Кроме того, в рассматриваемой работе в результатах расчета не показана сама воксельная сетка, хотя оговаривается, что размер вокселя равен 0,2 мкм. Наконец, ограниченностью работы является то, что в ней рассмотрен только однонаправленный волоконно-армированный композит. В работе [21] рассматриваются короткие случайно расположенные в пространстве волокна, а также введены некоторые толщины граничной области волокно - матрица, полученные картины результатов моделирования такой композитной структуры представляются достаточно адекватными реальным композитам. Однако и здесь не удалось обнаружить самой воксельной сетки.

В контексте поставленной задачи интерес представляет еще одна публикация, посвященная описанию структуры костей живых организмов [22]. Автор публикации, используя воксельный подход, описывает материал с порами в виде прямоугольных параллелепипедов. Представительный объемный элемент в форме куба имеет на каждой грани по четыре сквозных отверстия также квадратной формы в поперечном сечении. Используя такой подход, применяя вместо указанных пор волокна, можно получить заготовку из ВКМ объемного плетения ортогональной структуры. Автор анализируемой публикации не приводит зависимости по моделированию такой структуры, но именно данный подход и был использован в предлагаемой здесь новой работе.

Рассматривая вопрос моделирования процесса резания лезвийным инструментом, нельзя не проанализировать публикации, посвященные собственно физическому моделированию, включая как численные сеточные методы, такие как МКЭ, так и бессеточные методы типа SPH. Данный анализ был произведен авторами настоящей публикации в первой ее части. Такой анализ показал, что SPH-метод находит все более широкое применение в расчетах процессов с разрушением деталей, к которым относится и процесс резания лезвийным инструментом. Реализация этого метода, расчетные зависимости которого введены в используемой программе LS-Dyna, и будет применена далее для решения поставленной задачи.

Вышеприведенный обзор литературных источников показал следующее . Во-первых, во-ксельное моделирование как наиболее гибкий и устойчивый в вычислительном плане метод моделирования все шире применяется в исследовательской практике. Данный метод позволяет решать не только геометрические задачи, но и развивается в задачах расчета напряженно-деформированного состояния композитных деталей без использования традиционных сеточных и бессеточных методов расчета. Во-вторых, воксельное моделирование, применяемое как для дисперсно-, так и для волоконно-армированных композитов, позволяет максимально адекватно описать форму наполнителей и граничных слоев наполнитель - матрица. В-третьих, пока не удалось обнаружить воксельных моделей (их математических зависимостей) для заготовок из ВКМ объемного плетения с описанием граничных слоев.

Постановка проблемы и формулирование гипотезы

В связи с указанными выше тезисами развитие теории воксельного микромоделирования волоконно-армированных заготовок объемного плетения с последующим физическим моделированием их лезвийной обработки на основе бессеточного SPH-метода расчета является актуальной задачей машиностроения. Для ее решения необходимо создать численные микромодели таких заготовок из ВКМ объемного плетения, включая моделирование граничных слоев волокно – матрица, и последующего применения SPH-метода расчета. В последнем случае планируется применить модель материалов Джонсона–Кука с набором параметров, описанных по результатам исследований в предыдущей части статьи. Полученные модели стружкообразования, позволяющие определить напряженно-деформированное состояние в окрестности зоны резания при различных условиях резания, позволят качественно оценить адекватность принятых подходов, что в дальнейшем позволит получить наборы результатов в широком диапазоне параметров и условий обработки, а также сделать практические выводы.

Методология исследования

Для решения поставленной задачи численного моделирования стружкообразования при резании лезвийным инструментом заготовки из ВКМ объемного плетения на первом этапе – этапе геометрического моделирования таких заготовок – планируется использовать метод воксельного моделирования, а на втором этапе – этапе расчета напряженно-деформированного состояния – планируется использовать совместно подходы SPH-метода и метода конечных элементов.

Структура работы

В первой части результатов этого этапа исследования будут приведены зависимости и результаты геометрического моделирования заготовок из ВКМ объемного плетения ортогональной структуры, а во второй части приведены результаты расчета напряженно-деформированного состояния рассматриваемой заготовки при резании ее лезвием стального инструмента.

Геометрическое моделирование заготовки из ВКМ объемного плетения ортогональной структуры

При моделировании такой заготовки прежде всего необходимо выбрать ее характеристики. К числу одной из ранних работ, в которой приведены примеры использования металлических композитов, описания их структуры и особенности разрушения, следует отнести книги 1993 и 1995 г. [23, 24]. В последней отмечается, что диаметр используемых волокон может достигать 800 мкм. Однако наиболее качественные фотографии волокон, граничного слоя и матрицы таких композитов приведены в другой работе [25]. Там же даны сведения о размерах стального волокна. Указано, что его диаметр равен 152 мкм. Одна из фотографий волокон в окружении граничного слоя и матрицы приведена на рис 1.

Как видно из рис. 1, толщина граничного слоя составляет примерно 10 % от диаметра волокна и равна около 16 мкм. Если принять, что данный граничный слой будет описываться всего одним конечным элементом или одной частицей SPH-метода расчета, то само волокно будет описано примерно 10 частицами. Как минимум одна частица нужна для описания матрицы в зазоре между граничными слоями двух соседних волокон. При моделировании всего трех волокон потребуется 14 х 3 = 42 частицы по одной из координатных осей. Для всех трех осей потребуется 42³ = 74 088 частиц. Для решения задачи деформации упругой области с использованием тривиального закона Гука такая размерность не представляет собой вычислительных трудностей.

Рис. 1. Волокно из нержавеющей стали и матрица из алюминиевого сплава [23]

Fig. 1. Stainless steel fiber and aluminum matrix [23]

Однако решение задачи упруго-пластических деформаций с разрушениями в условиях контактного взаимодействия двух тел с учетом более сложной модели материала Джонсона–Кука является намного более сложным вариантом расчета. Такой расчет потребует десятков часов работы многоядерного процессора. С учетом данных обстоятельств можно признать, что при моделировании процесса резания композитной заготовки целесообразно ее описание с вышеуказанным количеством волокон в выбранной ее области пространства. Исходя из этого, был выбран следующий вариант геометрического моделирования фрагмента такой заготовки.

В выбранной системе координат заготовки X, Y, Z волокно с осью, расположенной вдоль оси Z , будет определяться каноническим уравнением цилиндра:

R ²< ( x - A -)² + ( y - B i ) ² <  R ₂ ² ,                                                               (1)

где для волокна R 1 = 0, а x , y , A i , B i - координаты точек данного цилиндра и координаты центра его базовой i -й окружности в плоскости X , Y ; R ₂ - радиус этого цилиндра, равный радиусу волокна R f ₂ . Для моделирования, например, девяти таких волокон величина i = 1...9 . Для любого числа волокон i = 1... Nz , где Nz - общее количество волокон в выбранном направлении.

следует использовать и для расчета цилиндров граничного слоя волокно - матрица, при этом R ₁

становится радиусом волокна Rf 2, а R2 - максимальный радиус граничного слоя Rb2. Очевидно, что модель такого ВКМ объемного плетения ортогональной структуры будет определяться величинами Ae, Be (e = i, j, k), которые представляют собой параметры, зависящие от расстояний между осями смежных волокон. Эти величины зависят от требуемой объемной доли наполнителя в композите. Кроме того, поскольку волокна не должны пересекаться между собой, то в случае равномерного расположения данных волокон эти расстояния должны быть равны Ae = Be = 2 Rb 2 при условии, если между граничными слоями отсутствуют элементы матрицы. Если моделировать наличие последних, то к правой части приведенного равенства нужно добавить такое удво- енное расстояние для матричного промежутка между волокнами.

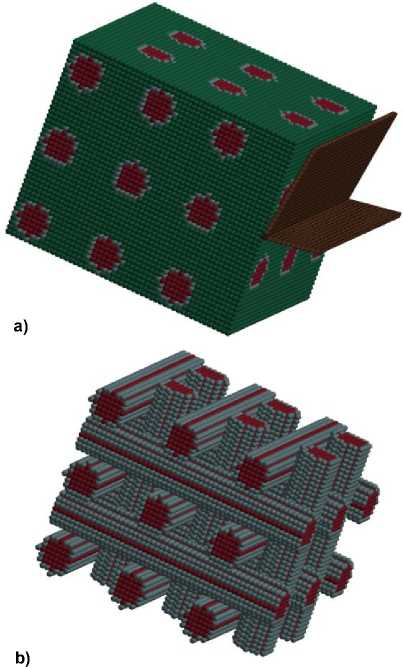
Рис. 2. Сетка конечных элементов резца, множество вокселей матрицы, волокна и граничного слоя (а) и отдельно последние (b)

Fig. 2. Finite elements of the cutter, a set of voxels of the matrix, fiber and boundary (a) and separately the latter (b)

Первоначально принимается, что параметры состояний всех вокселей в рассматриваемой модели равны трем P ( x , у , z ) = 3, то есть все они принадлежат матрице, для которой выбран номер «три». Условием принадлежности вокселя к волокну - его номер примем равным единице - является равенство его параметра состояния так же единице: P ( x , у , z ) = 1 при выполнении условия (1) для волокна. Аналогично условием принадлежности вокселя к граничному слою является равенство его параметра состояния двум: P ( x , у , z ) = 2 при выполнении условия (1) для такого слоя. При необходимости моделирования данного композита с воздушными порами (необходимы соответствующие уравнения для пор [11]) принимается значение параметра состояния: P ( x , у , z ) = 0 . В заданной области пространства в форме прямоугольного параллелепипеда по приведенным выше условиям рассчитывается множество параметров состояний воксе-лей P ( x , у , z ) , которое и представляет собой геометрическую модель композита, содержащую в себе узловые точки этих вокселей.

Использование данных зависимостей в компьютерной программе позволило рассчитать указанное множество и на этой основе получить множество во-кселей композита (рис. 2). Сетка конечных элементов для передней и задней поверхностей режущего клина резца рассчитывалась традиционными способами в один слой, поскольку резец в данном случае был принят абсолютно жестким телом.

Физическое моделирование резания заготовки из ВКМ объемного плетения ортогональной структуры

Полученная выше воксельная модель при минимальных математических преобразованиях становится и SPH-моделью, поскольку воксели совпадают с SPH-частицами. Материалы волокон, граничных слоев и матрицы описываются моделью Джонсона–Кука с выбранными в первой части статьи параметрами [1, 2]. Шаг воксельной сетки был принят равным 0,08 мм. Среди других параметров модели резания приняты параметры резца: передний и задний углы по 10°. Радиус округления режущей кромки имел двукратную величину от шага воксельной сетки. Толщина граничного слоя равна шагу сетки. Диаметр волокон равнялся 6 таким шагам. Между смежными точками граничных слоев слой матрицы не предусматривался. Длина заготовки равнялась 50 шагам сетки, ширина и высота – по 42 слоя. Все остальные параметры рассчитывались в единицах длины шага воксельной сетки. Заготовка закреплялась по всем шести степеням свободы по нижней ее грани и по грани, противоположной той грани, которая контактирует с резцом. При этом по высоте эта область закрепления была равна высоте подъема режущей кромки резца над нижней гранью заготовки. Скорость перемещения резца приравнивалась к 40 000 шагов сетки в секунду.

Первоначально для выполнения некоторой верификации было произведено моделирование резания гомогенной заготовки из алюминиевого сплава матрицы. Глубина срезаемого слоя приравнивалась к пяти шагам сетки. Результаты моделирования для некоторой начальной, промежуточной стадий резания и окончания обработки показаны на рис. 3. По рис. 3 видно, что характер деформаций и напряжений в целом отвечает принятым картинам для аналогичного типа резания.

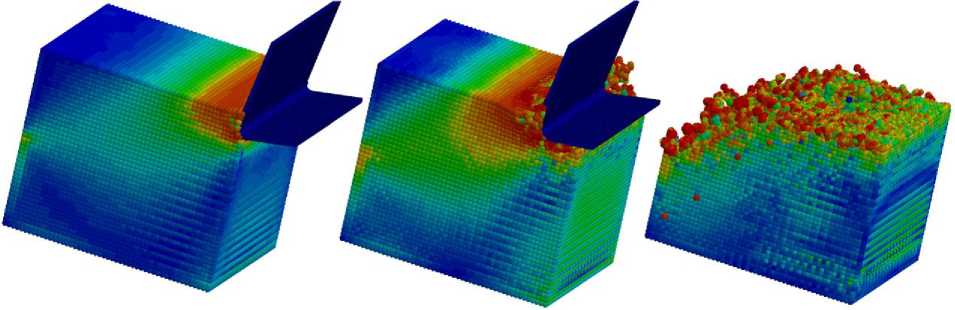
Рис. 3. Расчет напряжений по Мизесу для разных стадий резания гомогенной заготовки из 6061-T6

Fig. 3. Calculation of von Mises stresses for different stages of cutting a homogeneous workpiece made of 6061-T6

На следующем этапе было произведено моделирование резания рассматриваемого композита с одинаковыми параметрами волокна и граничного слоя [2]. Глубина резания t первоначально принималась равной половине высоты h заготовки (рис. 4).

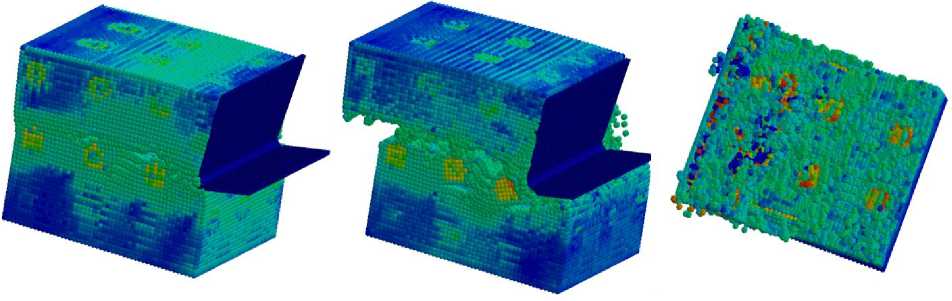
Рис. 4. Расчет напряжений при t = 0,5h для разных стадий резания заготовки ВКМ (справа представлен вид сверху)

Fig. 4. Stresses calculation at t = 0.5h for different stages of cutting a FRC workpiece (top view on the right)

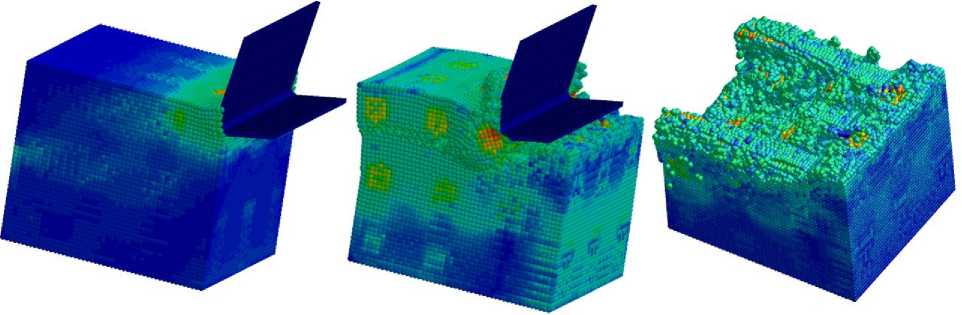
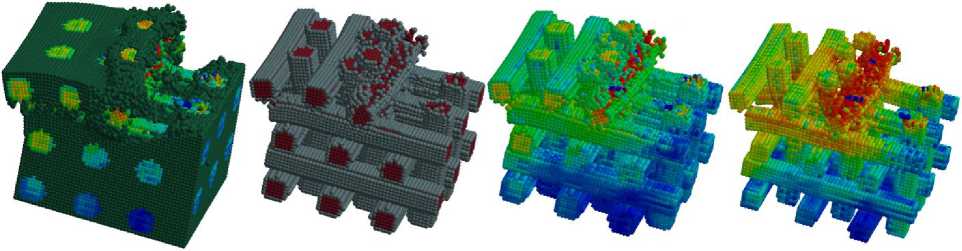
Для этих же условий было выполнено моделирование стружкообразования с глубиной резания, равной одиннадцати шагам воксельной сетки (рис. 5а) и далее с глубиной, равной пяти шагам сетки (рис. 5b). Резание моделировалось до положения резца, полностью вышедшего их заготовки. На рис. 6 приведены картины деформаций и напряжений по Мизесу в волокнах и граничном слое в среднем положении резца. На рис. 6а даны такие напряжения, при этом матрица имеет постоянный, не связанный с напряжениями цвет. На рис. 6b показаны перемещения SPH-частиц волокон и их граничных слоев. На рис. 6c дано то же самое с отражением в них напряжений по Мизесу. Наконец, на рис. 6d показано аналогичное, но только для самих волокон.

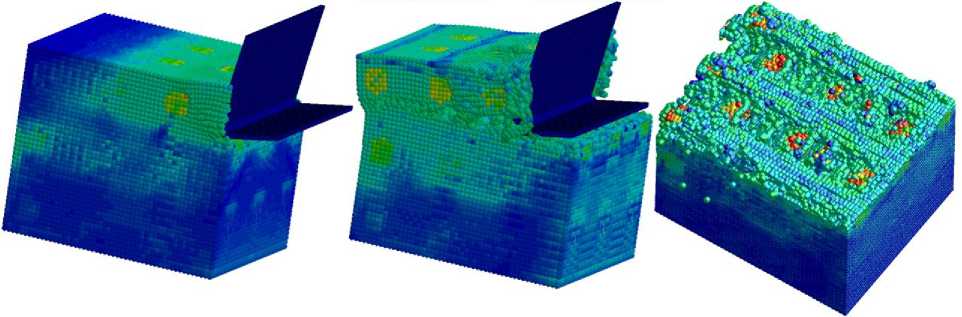
a) t = 0.25 h

b) t = 0.12 h

Рис. 5. Расчет напряжений по Мизесу для разных стадий резания заготовки ВКМ (справа представлен вид сверху)

Fig. 5. Calculation of von Mises stresses for different stages of cutting a FRC workpiece (top view on the right)

а)

b)

c)

d)

Рис. 6. Расчет напряжений по Мизесу для разных стадий резания заготовки ВКМ (справа представлен вид сверху)

Fig. 6. Calculation of von Mises stresses for different stages of cutting a FRC workpiece (top view on the right)

Для определения степени влияния параметров модели материла на результаты расчета последний вариант был пересчитан с новыми параметрами для граничного слоя волокно – матрица. Такие параметры для сплава 6061-T6 были выбраны из статьи, рассмотренной в первой части данной работы [1]. Результаты моделирования показаны на рис. 7. Как видно из рис. 5 и 7, в результатах расчета отличаются не только картины напряжений и деформаций, но и характер скола части заготовки при выходе из нее лезвия резца.

Для верификации полученных результатов моделирования целесообразно сравнить их с данными, полученными экспериментально. Как отмечалось в первой части статьи, результатов обработки заготовок из ВКМ объемного плетения найти в литературе пока не удалось. В связи с этим полученные нами результаты были сопоставлены с экспериментальными данными, полученными при резании заготовки из однонаправленного ВКМ [26]. В натурных экспериментах металлическая матрица Ti-6Al-4V была армирована керамическими волокнами SiC. Обработанные в разных плоскостях по отношению к направлению волокон поверхности показаны на рис. 8 слева. Поверхность, полученная моделированием (случай по рис. 5а), показана на рис. 8 справа.

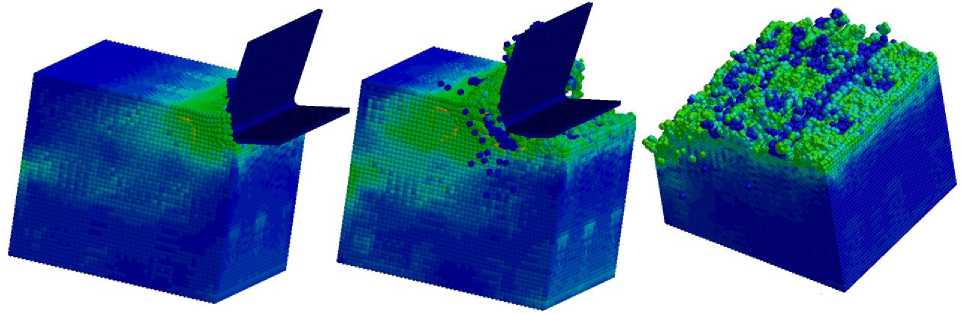
Рис. 7. Расчет напряжений для разных стадий резания заготовки ВКМ аналогично рис. 5 (с границами из [1])

Fig. 7. Stresses сalculation for different stages of cutting a FRC workpiece as Fig. 5 (with boundary material from [1])

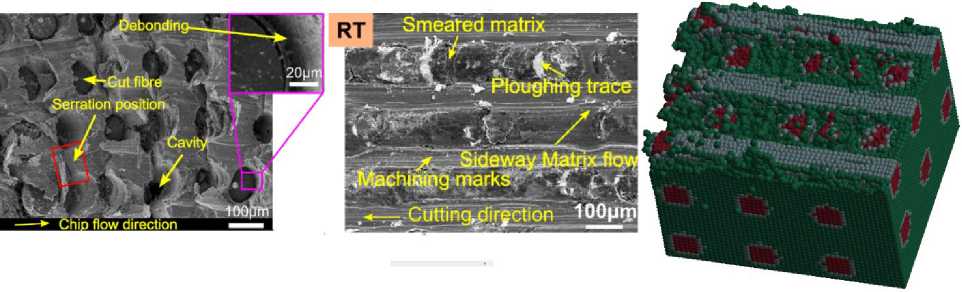
Рис. 8. Обработанная поверхность заготовки ВКМ [26] и смоделированная поверхность

Fig. 8. The machined surface of the FR composite workpiece [26] and the modelled surface

Результаты и обсуждения

Выполненное моделирование процесса резания лезвийным инструментом заготовки из волоконно-армированного композита объемного плетения показало следующее. При моделировании резания заготовки из гомогенного алюминиевого материала максимальные напряжения, как и следовало ожидать, расположены напротив передней поверхности резца, при этом можно четко различить линию раздела напряженной зоны вдоль плоскости сдвига (см. рис. 3). При продвижении резца в заготовку под его задней поверхностью у его режущей кромки также наблюдается ожидаемый всплеск напряжений. По окончании резания режущий клин «выламывает» заметную часть заготов- ки, что также соответствует ожидаемому результату. Таким образом, подобранная для матрицы композита модель материала и ее параметры в целом представляются адекватными.

При анализе результатов моделирования резания композита сразу же необходимо отметить, что в данной работе изучался случай резания с ортогонально расположенными волокнами, оси которых совпадают с осями инструментальной системы координат и параллельны граням обрабатываемой заготовки. Кроме того, следует отметить и сравнительно малые размеры последней по сравнению с размерами волокон и глубиной резания. Таким образом, полученные результаты можно пока рассматривать как предварительные в общей теме моделирования резания заготовок из ВКМ объемного плетения.

Моделирование лезвийной обработки заготовки из рассматриваемого ВКМ с достаточно большой глубиной резания показывает, что наблюдается отделение припуска по плоскости, расположенной между взаимно перпендикулярными горизонтальными волокнами. По-видимому, образовалась трещина сразу на всю длину данной заготовки, по которой и произошло отделение снимаемого слоя (см. рис. 4). Такой результат тоже можно признать ожидаемым, однако такое отделение припуска не является характерным для обработки резанием. В большей степени это соответствует резке листового металла гильотинными ножницами.

Уменьшение глубины резания позволило получить картины напряженно-деформированного состояния, более близкие к типичной обработке лезвийным инструментом. Перед режущим клином также можно выделить зоны с повышенным напряжением, однако картины его распределения заметно отличаются от аналогичных картин при резании заготовок из гомогенных материалов (см. рис. 5). Максимальные напряжения возникают прежде всего в волокнах, поскольку они более прочные и, как и следует ожидать, в большей степени сопротивляются разрушению, сохраняя в себе большие, чем в матрице напряжения. Достаточно интересным оказался результат моделирования в момент выхода резца из заготовки: волокна образовали вместе с матрицей достаточно прочную конструкцию в некоторой области между продольным к вектору скорости главного движения волокнами. В результате в этом месте образовалось сравнительно большое углубление (см. рис. 5b, справа). Такие углубления даже при сравнительно малой глубине резания заметно портят кромку на получаемой детали. В то же время при резании с большей глубиной не наблюдается существенного ухудшения кромки детали. Данное сравнение позволяет сделать вывод о важности характера расположения волокон по отношению к режущему лезвию инструмента.

Анализ картин деформаций и разрушения волокон, показанных выше на рис. 6, позволяет сделать вывод о том, что после разрушения лезвием матрицы композита расположенные в этом месте волокна разрушаются в зависимости от их расположения в пространстве. Волокна, оси которых расположены перпендикулярно плоскости резания, разрушаются следом за матрицей, которая их охватывает в данном месте. Волокна с осями, параллельными главной режущей кромке, в целом сохраняются и либо уносятся в стружку, либо смещаются дальше в зону обработки, вдавливаясь в материал матрицы. Волокна, находящиеся под задней поверхностью резца, вдавливаются в обработанную поверхность. Наконец, волокна, оси которых параллельны вектору скорости главного движения резания, либо, изгибаясь, уносятся в стружку подобно ламинату, либо подминаются задней поверхностью инструмента и вдавливаются в обработанную поверхность заготовки.

Попытку заменить параметры модели материала граничного слоя между волокном и основным составом матрицы также можно рассматривать как предварительное исследование. Выдвинутая в первой части статьи гипотеза о том, что граничный слой является менее прочным, чем основной слой матрицы, и поэтому достаточно применить параметры модели Джонсона-Кука, дающие кривую упрочнения, расположенную несколько ниже аналогичной кривой для остальной части матрицы, требует своего дальнейшего изучения специалистами в области материаловедения. В качестве результата рассматриваемого моделирования можно лишь констатировать факт, что картина напряженно-деформированного состояния при резании заметно отличается от аналогичной картины с другими параметрами указанной модели. Можно высказать предположение, что если в первых случаях (см. рис. 4–6) матрица через такой же граничный слой давит на волокна, деформирует их и смещает, то во втором случае граничный слой сразу же разрушается, резец начинает воздействовать непосредственно на сами волокна, опертые с другой стороны на матри-

Вольф Г.В.

цу, и происходит большее разрушение данных волокон. При моделировании наблюдалось даже резание волокон, расположенных параллельно режущей кромке, что представляется сомнительным вариантом реализации такого резания. Таким образом, определение параметров модели материала граничного слоя волокно – матрица требует более тщательного изучения, поскольку оказывает заметное влияние на результат всего моделирования.

Сравнение картин обработанной поверхности, полученных натурными экспериментами и моделированием, в целом показывает их сходство (см. рис. 8). Однако здесь необходимо принять во внимание два обстоятельства. Первое, в натурном эксперименте обрабатывалась заготовка из однонаправленного волоконно-армированного композита. Второе, материалы компонентов такого композита в натурном эксперименте существенно отличались от более мягких материалов композита для случая моделирования. Следовательно, необходимо или найти подходящие модели материалов и их достоверные параметры, отвечающие случаю натурного эксперимента, или получить результаты натурного эксперимента, соответствующие случаю компьютерного моделирования. С учетом этого можно все же отметить, что выбранный подход для моделирования процесса резания рассматриваемых заготовок из ВКМ является перспективным и требует дальнейшего продолжения этих исследований как метода прогнозирования качества обработанных поверхностей и выбора рациональных параметров технологической операции и ее стратегии обработки.

Выводы

• 1.    В целом полученные численными геометрическим и связанным с ним физическим видами моделирования картины деформаций и напряжений лезвийной обработки заготовки из ВКМ объемного плетения ортогональной структуры отвечают ожидаемым; принятый подход как метод прогнозирования качества обработанных поверхностей и выбора рациональных параметров технологической операции и стратегии обработки является перспективным и требует своего дальнейшего развития.

• 2.    Характер напряженно-деформированного состояния зоны резания при обработке заготовки из рассматриваемого ВКМ заметно отличается от характера такого состояния в случае заготовки из гомогенного материала. Существенное влияние на это оказывают волокна, которые в меньшей степени, чем матрица, деформируются и разрушаются от действия резца.

• 3.    В процессе резания участки волокон могут сохраняться и либо выходить из зоны резания со стружкой, либо вдавливаться в обработанную поверхность, либо перемещаться вместе с зоной резания до последующего выхода по одному из двух вышеуказанных вариантов.

• 4.    Участки волокон могут оказывать армирующее воздействие на сопредельные объемы матрицы, что приводит к большим сколам у кромок заготовок, которые формируются при выходе из них лезвия инструмента. Уменьшение глубины резания может не уменьшать размеры таких сколов, что определяется характером расположения волокон у кромки выхода инструмента.

• 5.    Параметры выбранной модели материалов для описания граничного слоя волокно – матрица оказывают заметное влияние на характер напряженно-деформированного состояния зоны резания. Необходимо дальнейшее материаловедческое изучение данного вопроса.