Численное моделирование высотомера малых высот с использованием генетического алгоритма для расчета частот дополнительной модуляции

DOI:

Высотомеры малых высот, построенные по схеме измерения частоты биений сигналов с частотной модуляцией (ЧМ-высотомеры), отличаются простотой технической реализации, однако обладают существенным недостатком — т.н. «дискретной ошибкой», определяемой девиацией частоты А ш и носящей методический характер [4; 6]. Одним из наиболее простых средств подавления дискретной ошибки является использование дополнительной модуляции средней частоты сигнала [5; 7].

В стандартном ЧМ-высотомере циклическая частота ш (t) со временем изменяется по гармоническому закону. При этом зависимость показаний счетчика от высоты R (рабочая характеристика высотомера) для несущей частоты / 0 = Щ ⁰ = 450 МГц и девиации А/ = ^Щ = 25 МГц приведена на рисунке 1.

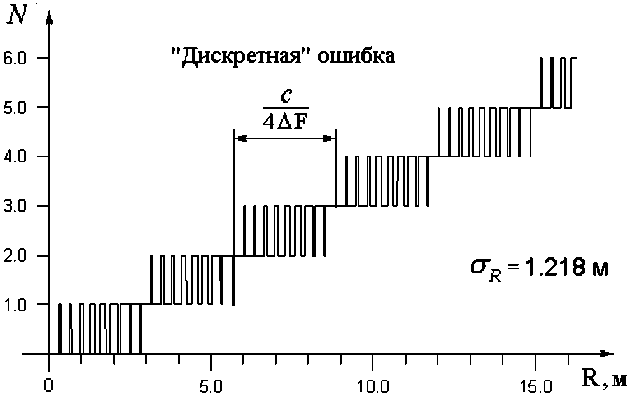
Рис. 1. Рабочая характеристика ЧМ-высотомера

Среднеквадратическое отклонение o r зависимости N (R) от линейной составляет 1,218 м, что в ряде практических приложений не обеспечивает требуемой точности.

Наиболее простым способом подавления дискретной ошибки ЧМ-высотомера является введение дополнительной модуляции — изменение частоты несущей в каждом периоде основной модуляции Т = 2 п и усреднение результатов счета на достаточно большом интервале наблюдения [3; 7]. При использовании дополнительной частотной модуляции показания счетчика высотомера составляют величину

N (F k , т ) =

Ш о т + А шт         ш о т - А шт

---------+ Fk т - ---------+ Fk т где Fk — значение дополнительной частотной добавки в к-м периоде; т = 2R — задержка зондирующего сигнала на дальности R. При этом усреднение показаний происходит за М периодов частоты дополнительной модуляции:

А м

^N ^ = M^^{N ( F} k , ^{т )} ,

^М k=1

где М = 2т четное.

Простейшей формой дополнительной частотной модуляции F (t) является линейная F _k = ^2 i , 1 — 1) AF , предполагающая равномерное распределение частот F _k на интервале F _k Е [ — AF; AF] . При одинаковых девиациях частот основной и дополнительной модуляции ( 25 МГц) среднеквадратическое отклонение рабочей характеристики высотомера N (R) от прямой в диапазоне высот 3-15 м составляет o r = 0,121 м (см. рис. 2).

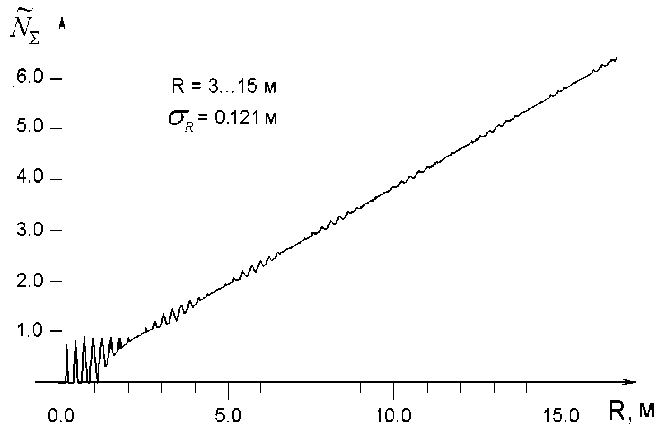
Рис. 2. Рабочая характеристика высотомера при линейной дополнительной частотной модуляции. Девиации частоты основной и дополнительной модуляции выбраны одинаковыми ( А/ = AF = 25 МГц).

Как отмечалось ранее [3], линейный закон изменения частоты дополнительной модуляции не является максимально эффективным.

1.    Использование генетического алгоритма для оптимизации частот дополнительной частотной модуляции

Поиск оптимального набора частот дополнительной модуляции осуществлялся с помощью генетического алгоритма [1; 2] с учетом симметрии задачи:

W _i , 1 <  г <  m,

где W _i — элемент генотипа { W _i } одного индивида (потенциального решения) в виде набора частот {F _i } . Этот соответствующий индивиду набор имеет вид:

F i = (Wi , [ —W M +1 -i ,

г <  m ;                             (3) г > m.

Как и частоты, параметры индивидов ограничены условием:

— AF <  W _i <  0.                               (4)

Дополнительно, без потери общности, накладывается условие упорядоченности:

г < j ^ W _i <  W j .

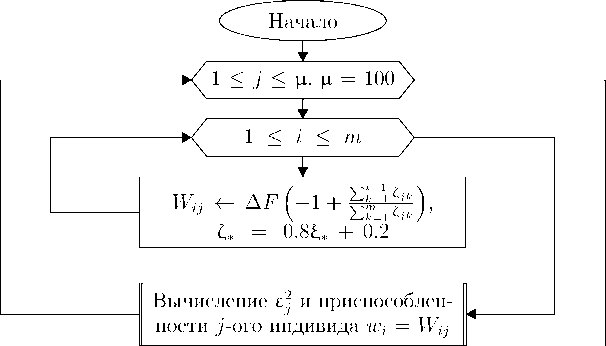
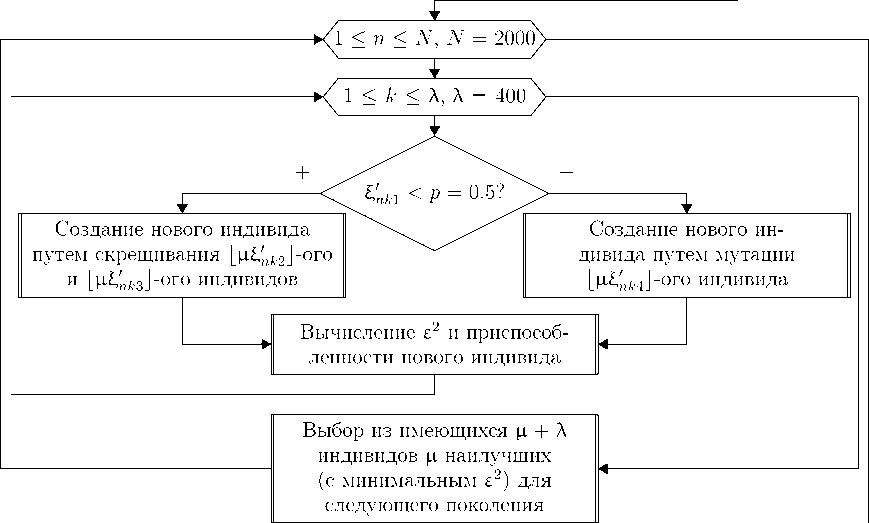
Далее использовалась эволюционная стратегия [8] ц + Л : следующее поколение (набор потенциальных решений) генетического алгоритма выбирается из индивидов текущего и большого количества производных от них экземпляров. Блок-схема алгоритма представлена на рисунке 3, где Е * , Е * — равномерно распределенные на интервале [0; 1) независимые случайные величины.

При оптимизации были использованы следующие параметры генетического алгоритма:

• •    размер популяции, а также количество индивидов текущего поколения, принимающих участие в отборе ц = 100 ;

• •    количество производных индивидов в каждом поколении Л = 400 ;

• •    вероятность получения нового индивида путем мутации р = 0,5 ;

• •    вероятность получения нового индивида путем скрещивания 0,5 (равна 1 — р для схемы ^Ц + ^{Л )}.

Оператор мутации был определен следующим образом: каждая частота с вероятностью 0,2 изменяется на нормально распределенную случайную величину со стандартным отклонением ст = =М. При выходе W _i из границ (4) выполняется ее зеркальное отражение от этих границ до тех пор, пока она не окажется внутри, т.е. выполняется преобразование:

w ’ = AF

+— arcsin π

(^{sin п} (AF⁺D)

Такой способ обеспечения ограничения (4) предназначен для исключения возможной системной предвзятости в пользу граничных точек при альтернативных ограничениях, например:

W?

—-F

0 ,

W _i < AF ;

W i > 0;

^W i ,     в остальных случаях .

В завершение процедуры мутации частоты производится сортировка для выполнения условия (5). Скрещивание выполняется путем слияния наборов значений двух индивидов в общий массив, сортировки массива и разбиения его на подряд идущие пары, в каждой из которых одно значение помещается в один из порождаемых индивидов, а другое — в другой (какое из двух значений окажется в каком индивиде, выбирается случайным образом). Легко видеть, что при этом за счет первоначальной сортировки условие (5) выполняется автоматически.

________ ^

Вывод оптимизированных наборов {F/,}

Рис. 3. Блок-схема генетического алгоритма оптимизации набора частот дополнительной модуляции высотомера малых высот

Набор частот дополнительной модуляции, полученных с использованием генетического алгоритма, представлен на рисунке 4. Приведенные результаты получены после моделирования 2000 поколений.

Рис. 4. Значения частот дополнительной модуляции, полученные с помощью генетического алгоритма ( = 100 , AF = 25 МГц)

Рабочая характеристика высотомера малых высот, полученная численным моделированием с использованием оптимизированного набора частот дополнительной модуляции приведена на рисунке 5.

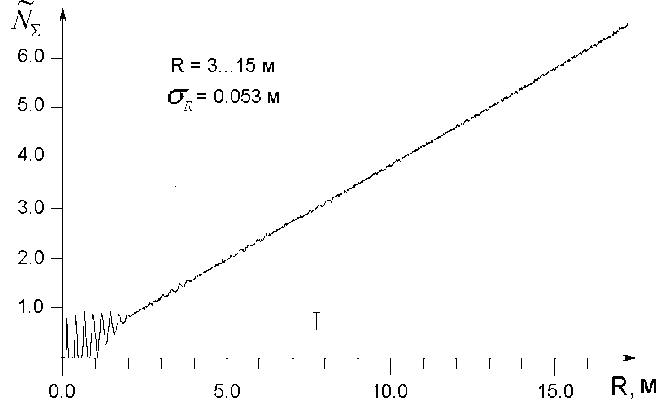
Рис. 5. Рабочая характеристика высотомера при дополнительной частотной модуляции, полученной с использованием генетического алгоритма (A f = AF = 25 МГц)

Сравнение зависимостей на рисунках 2 и 5 показывает, что в последнем случае погрешность отклонения от прямой зависимости N (R) существенно ниже по сравнению с линейным законом изменения дополнительной частотной модуляции при тех же ограничениях на занимаемую полосу частот.

Заключение

Таким образом, использование генетического алгоритма для оптимизации набора частот дополнительной частотной модуляции в высотомере малых высот позволило более чем в два раза повысить точность измерения расстояния по сравнению с линейной формой без расширения занимаемой полосы частот. Последнее обстоятельство особенно важно при жестких условиях на электромагнитную совместимость бортовых систем автоматической посадки.

Значения элементов массива оптимизированных частот могут быть рассчитаны заранее для конкретных условий эксплуатации. Хранение в памяти большого числа значений частот и их оперативное использование при работе синтезатора не представляет сложности для средств бортовой компьютерной техники.