Численный алгоритм поиска оптимальных условий протекания каталитической реакции

Применение методов математического моделирования для расчета и анализа процессов химической промышленности позволяет определять оптимальные условия их ведения. Оптимизация каталитических процессов является ключевым аспектом в химической инженерии и промышленной химии, так как она позволяет улучшить эффективность процессов и снизить материальные затраты. Поэтому разработка математических методов определения оптимальных значений параметров каталитических процессов и программных средств, позволяющих проводить виртуальные эксперименты с различными условиями и экономить время и ресурсы, является актуальной задачей и представляет научный интерес.

Оптимизация каталитических процессов является комплексной задачей, включающей в себя подбор оптимальных условий для проведения реакций, подбор наиболее эффективных катализаторов и их концентраций, управление временем, температурой, скоростью подачи сырья. Для определения оптимальных условий используются различные математические методы.

Линейное программирование применяется для решения таких задач химической технологии, как рациональное распределение сырья между различными процессами, определение наиболее экономичного способа производства химической продукции и др. [1, 2]. Для решения задач оптимального управления каталитическими процессами применение методов линейного программирования ограничено ввиду нестационарности процессов и нелинейности их математического описания.

Применение аналитических методов для решения задач оптимизации, таких как принцип максимума Понтрягина, вариационные методы [3, 4] и др., при достаточно большом числе независимых переменных сопряжено с рядом трудностей вычислительного характера, связанных с технологическими особенностями химических процессов.

В тех случаях, когда химический процесс можно разбить на последовательность взаимосвязанных этапов, для поиска оптимальных значений параметров можно использовать динамическое программирование [5]. Однако для сложных химических реакций, описываемых системами дифференциальных уравнений высокой размерности, использовать его нецелесообразно ввиду ресурсоемких вычислений.

В настоящее время для решения сложных оптимизационных задач применяются методы эволюционных вычислений [6–8], одним из которых является метод дифференциальной эволюции [9–11]. При использовании данного метода не требуется вычислять градиенты функции, а благодаря механизмам мутации и скрещивания он способен преодолевать попадание в локальный экстремум.

В задачах оптимального управления каталитическими реакциями параметры управления могут представляться в виде констант (например, продолжительность реакции, мольное соотношение реагентов) или в виде функций (например, температура, давление). Целью работы является разработка численного алгоритма, позволяющего осуществлять одновременный поиск оптимальных значений управляющих параметров-функций и параметров-констант.

1. Постановка задачи

Пусть динамика состояния каталитической реакции определяется системой дифферен-

циальных уравнений: dx = f (t,x(t),T (t))                                      (1) с начальными условиями xj(0) = xj, j = 1,n,                                     (2) где x(t) = (xi(t), Х2(t),..., xn(t))T — вектор фазовых переменных, t G [0, tend] - время, T(t) -температура, f (t,x(t),T (t)) = (fi (t,x(t),T (t)),f2 (t,x(t),T (t)),...,fn (t,x(t),T (t)')')T -вектор-функция, непрерывная вместе со своими частными производными.

Начальные условия (2) выражают состав реакционной смеси в начальный момент времени t = 0 .

Пусть концентрации реагентов выражены в мольных долях. Тогда их значения связаны соотношением:

n

E X j (0) = ^L                                  (3)

j =1

В качестве управляющих параметров рассмотрим температуру реакции T ( t ) , длительность процесса t end и начальные концентрации веществ в исходной смеси x (0) = ( x i (0) ,X 2 (0) ,... ,x n (0)) . Пусть на их значения наложены ограничения:

T min ≤ т ( t ) <  T max ,   t ^{G [0 ,} t end ] ,

t min ≤ t end ≤ t max ^,

0 <  x j (0) <  1 , j = 1 ,n.

Требуется для реакции определить температурный режим T * ( t ) , время контакта веществ t * _n d , вектор начальных концентраций реагентов x * (0) = ( x * (0) ,x 2 (0) ,... ,х П (0)) , удовлетворяющие условиям (3) – (6) и обеспечивающие достижение максимального значения целевым функционалом

G ( T * ( t ) ,t * nd ,x* (0))= g ( x ( t * nd)) , (7)

где g ( x ( t _end )) - непрерывно-дифференцируемая функция, x ( t _end ) - вектор концентраций веществ в конце реакции.

• 2.    Алгоритм определения оптимальных значений параметров каталитической реакции

Сформулируем численный алгоритм для определения значений параметров протекания каталитической реакции, используя метод дифференциальной эволюции.

Набор потенциальных решений оптимизационной задачи, называемый популяцией векторов-индивидов, подвергается воздействию операторов отбора, мутации и кроссовера. Затем рассматривается возможность перехода модифицированного вектора в новую популяцию.

Будем искать параметр управления T ( t ) в классе кусочно-постоянных функций управления. На интервале [0 , t end ] введем сетку дискретизации с шагом h = t end и узлами t o ,t 1 ,...,t _m , такими, что t o < t i < t ₂ < ... < t _m , t o = 0 , t _m = t end , в которых будем искать значения T ( t ) . Для получения промежуточных значений температуры используем кусочно-постоянную аппроксимацию

T ( t ) = T ( t k )= T k , t e [ t k ,t _{k +1}] , k = 0 ,m - 1 .

Введем в рассмотрение множество векторов-индивидов (особей):

Vi = (Ti0,Tn, ..., Tim-1 ,tendi ,Xi1(0), ..., Xin (0)), i = 1,S, каждый из которых представляет собой возможное решение задачи. Совокупность всех векторов Vi (i = 1,s) является популяцией. Введем обозначение для элементов вектора-индивида: Vi = (Vio ,Vii,..., Vir) = (Vj), j = 0, r, где

'T ij ,  j = 0 ,m - 1 ,

V ij =    ^t endi ^,

.x i (0) ,

j = m,_____ j = m + 1 , r,

r = m + n + 1 .

В качестве фитнес-функции, определяющей приспособленность каждой особи, выступает целевой функционал (7). Особь v k является более приспособленной, чем особь v l , если G ( V k ) >  G ( v i ) .

Поскольку вектор-индивид содержит значения нескольких параметров управления, то введем в алгоритм решения задачи (1) – (7) операцию нормировки для перехода к одинаковым ограничениям для всех компонентов вектора.

Алгоритм решения задачи (1) – (7) состоит из следующих шагов.

Шаг 1. Сформировать начальную популяцию векторов V i ( i = 1 ,s ) путем заполнения случайными значениями из диапазонов, задаваемых неравенствами (4) – (6):

T min + ^a ij ^(T max

-

T min ) ,

^V ij — * t min + ^a ij ^(t max

-

t min ) ^,

j = 0 ,m - 1 , j = m,

aij, j = m + 1,r, где aj e [0,1] — случайное число.

Установить счетчик итераций z = 1.   ___

Шаг 2. Для каждого вектора Vi (i = 1,s) проверить выполнение условия равенства r суммарной концентрации веществ единице (условие (3)). Если £ Vij = 1 (i = 1,s), то j=m+1

перейти на шаг 3, иначе пересчитать компоненты вектора V i , начиная с m +1 , так, чтобы они в сумме дали единицу:

V ij =

v ij

—---, j = m + 1 ,r.

Е Vik k=m+1

Шаг 3. Для каждого вектора V i ( i = 1 ,s ) рассчитать значение фитнес-функции (7).

Шаг 4. Вычислить компоненты нормированного вектора-индивида Vj (i = 1,s) по фор- мулам:

V ij =

( V ij ( V ij

v ij ^,

Tmin ) / (Tmax   Tmin ),  j — 0, m tmin )/(tmax   tmin ),   j — m, j = m + 1, r,

После выполнения шага 4 значения компонентов векторов V i удовлетворяют условию:

0 <  V j <  1 , i = 1 , s, j = 0 , r.

Шаг 5. Установить вектор-мишень v_m ish = v i .

Шаг 6. Среди векторов-индивидов, за исключением вектора-мишени v_mish , случайным образом выбрать четыре вектора V k , Vi , v p , v_q .

Шаг 7. Из оставшихся векторов-индивидов найти вектор v _max , которому соответствует наибольшее значение функции приспособленности.

Шаг 8. Из отобранных векторов создать вектор-мутант, рассчитываемый по формуле

^mut — Umax + ^(Vk + Vl — Vp - Vq), где ^ G [0, 5; 1] — параметр мутации, задаваемый пользователем [13].

Шаг 9. Проверить условие выхода значения компоненты вектора-мутанта за границы допустимого диапазона (8). Если v _mut j <  0 или v _mut j >  1 , то v _mut j — в, где в G [0 , 1] — случайное число.

Шаг 10. Проверить выполнение условия (3) для компонентов вектора-мутанта v _mut , являющихся начальными концентрациями. Если условие (3) не выполнено, то осуществить пересчет значений компонентов вектора-мутанта по формуле:

v mutj —

v mutj

r

Е

j — m + 1 , r.

k=m+1

v mutk

Шаг 11. Сгенерировать пробный вектор v prob :

) vmutj, Xj — Р, t Vmishj, Xj > р, j — 0, r,

где X j G [0 , 1] - случайное число, p G [0 , 1] - параметр скрещивания [13].

Шаг 12. Проверить выполнение условия (3) для последних n компонентов пробного вектора v _pro b , которые являются значениями концентраций взаимодействующих веществ. r

Если £ V probj — 1 , то пересчитать значения последних n компонентов пробного вектора, j = m +1

чтобы условие (3) выполнялось:

v probj —

v probj

r

IL Vprobk k=m+1

,

j — m + 1 , r.

Шаг 13. Вычислить значения управляющих параметров пробного вектора:

T min + ^V probj ^(T max

-

T min ) ,

j — 0 ,m - 1 ,

^v pr^{obj   <} tmin + V probj ^(t max

-

t min ) ,

j — m,

v probj ^,

j — m + 1 , r.

Шаг 14. Для пробного вектора v _prob вычислить значение фитнес-функции (7).

Шаг 15. Если вектор v _pro b является более приспособленным, чем вектор v_mi_s h , то вектор-мишень заменить вектором V prob. Иначе перейти к шагу 16.

Шаг 16. Если в качестве вектора-мишени рассмотрены все векторы текущей популяции, то перейти на шаг 17. Иначе v_mi_s h = v_mi_sh ₊i и перейти на шаг 6.

Шаг 17. Завершить вычисления, если на протяжении d поколений выполнены условия ( z >  2):                                _______________________________

r

Е ⁽vj ^(z)

- V ij ( z - 1)) ² <  E,

j =0

\G(Vi(z)) - G(Vi(z - 1))| < E, где Vi(z), Vi(z - 1) - векторы текущей и предыдущей популяций (i — 1,s), E - параметр завершения поиска решения. Иначе увеличить счетчик итераций z на 1 и перейти к шагу 5.

Шаг 18. Выбрать из последней популяции вектор V i с наибольшим значением фитнес-функции (7) и вычислить значения параметров:

T min + v ij ^(T max   T min ) , ^j — 0 ,m

1 ,

v ^ij     * t min + V ij ( t max

t min ) i ^j — ^m ,

V ij ,  j — m + 1 ,r.

Вектор v i является приближенным решением задачи (1) – (7).

Разработанный алгоритм учитывает ряд особенностей, связанных с физико-химическим смыслом задачи оптимального управления (1) – (7):

• 1)    на этапе формирования начальной популяции предусмотрен пересчет значений начальных концентраций в случае нарушения условия (3) (шаг 2);

• 2)    на этапе мутации проверяется условие выхода значений компонентов вектора-мутанта за границы допустимого диапазона (шаг 9);

• 3)    осуществляется проверка выполнения условия (3) для вектора-мутанта и пробного вектора, и производится пересчет значений их компонентов в случае нарушения условия равенства суммарной концентрации единице (шаги 10, 12).

• 3.    Вычислительный эксперимент

Найдем решение задачи оптимального управления реакцией синтеза бензилиденбензил-амина под действием FeCl 3 · 6H 2 O, математическое описание которой разработано в лаборатории математической химии Института нефтехимии и катализа РАН. Схема и кинетические уравнения стадий рассматриваемой реакции имеют вид [14]:

X 1 + X 2 ^ X 3 + X 4 , ^w 1 ^{(C,T ) — k} 1 ^{( T ) C} 1 C 2 , X 3 ^ X 5 + X 6 , w 2 ^{(C,T ) — k} 2 ^{(T ) C} 3 ,

X5 + X1 ^ X7 + X8, w3(C,T) — k3(T)C1C5, X8 + X6 ^ X9, W4(C, T) — k4(T)C6C8, где X1 – бензиламин, X2 – четыреххлористый углерод, X3 – хлорбензиламин, X4 – хлороформ, X5 – 1-фенилметанимин, X6 – хлористый водород, X7 – бензилиденбензиламин, X8 – аммиак, X9 – хлористый аммоний, Ci – значение концентрации i-го вещества (моль/л, i — 1, 9), kj - константа скорости j-й стадии реакции (л/(моль-ч) для j = 1, 3,4; 1/ч для j — 2), рассчитываемая исходя из уравнения Аррениуса:

kj (T) — ko exp ( - RET У где ko - предэкспоненциальный множитель (л/(моль-ч) для j = 1, 3,4; 1/ч для j = 2), Ej -значение энергии активации j-й стадии (Дж/моль), T – температура (К), R – универсальная газовая постоянная (8,31 Дж/(моль·К)).

Математическое описание реакции (11) представляется системой [14]:

dx i _ Fi ( x,T ) - X i F n ( x,T ) dt ^—         N

Fi — E Vij Wj,

j =1

dN              1 49

-d-— Fn(x, T)— v 52 Wj 52 Vij, j=1

с начальными условиями:

Xi(0) — x0, i — 1, 9, N(0) — 1,(14)

где Xi - концентрация i-го вещества, мольная доля (i — 1, 9); N — C/Co - относительное изменение числа молей реакционной среды, C и C0 – суммарная концентрация веществ и ее начальное значение, моль/л; (vij) - матрица стехиометрических коэффициентов (i = 1, 9, j = 1,4); Wj = Wj/Со - приведенная скорость j-й стадии реакции, 1/ч; V - объем реакционного пространства.

Значения кинетических параметров реакции (11) приведены в работе [14].

Исходными веществами реакции (11) являются X 1 и X 2 . Поэтому значения их концентраций в начале реакции должны удовлетворять условиям:

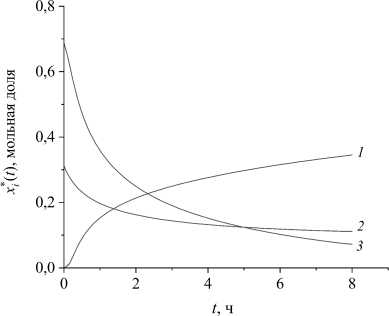
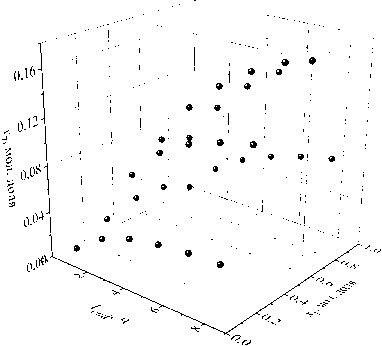
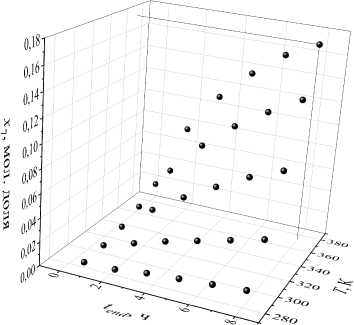
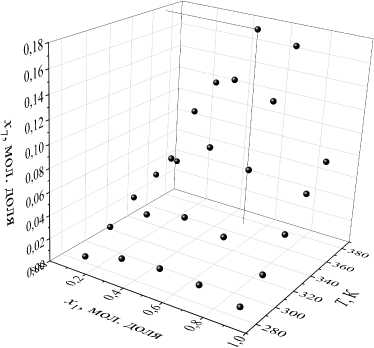
0

X1(0) + Х2(0) = 1.(16)

Концентрации остальных веществ:

Xi (0) = 0, i = 3,9.

На значения температуры и времени протекания реакции наложены ограничения:

285К < T(t) < 373К, t G [0, tend],(17)

0, 5ч < tend < 8ч.(18)

Требуется найти температурный режим T*(t), продолжительность реакции t*_nd и начальные концентрации реагентов x1(0), x2(0), удовлетворяющие условиям (15) - (18), при которых достигается наибольшая концентрация бензилиденбензиламина:

G(T * (tit end ,X (0)) = x7(tend) ^ max •

Решение задачи (11) – (19) найдено с помощью разработанного алгоритма со следующими параметрами: ^ = 0, 7, p = 0, 8, d = 5, e = 10^-3. Установлено, что наибольшую концентрацию бензилиденбензиламина, равную 0,345 мольных долей, можно получить при tend = 8 ч и начальных концентрациях реагентов (мольная доля):

x1(0) = 0, 688, x1(0) = 0, 312.                               (20)

При этом необходимо соблюдать температурный режим, показанный на рис. 1.

368 -

* 364-

G».

352 -

2           4     ’     6     '     8

Лч

Рис. 1. Оптимальный температурный профиль

На рис. 2 приведено изменение концентраций во времени бензилиденбензиламина и исходных веществ (бензиламина и четыреххлористого углерода). На рис. 3 показана значения концентрации бензилиденбензиламина, вычисленные при допустимых значениях начальной концентрации бензиламина от 0,1 до 0,9 мольных долей с шагом 0,2 мольные доли, для продолжительности реакции от 0,5 до 8 ч с шагом 1,5 ч и постоянной температуре, равной 373 К. Для указанного изотермического режима при начальных концентрациях реагентов X1(0) = X2(0) = 0, 5 мольных долей и продолжительности реакции, равной 8 ч, достигается наибольшее значение концентрации бензилиденбензиламина, равное 0,176 мольных долей.

На рис. 4 представлены результаты решения системы дифференциальных уравнений, полученные при начальных условиях (20), постоянной температуре, задаваемой значениями из промежутка (17) с шагом 22 К, и некоторых допустимых значениях длительности реакции. В этом случае наибольшее значение целевого функционала (19), равное 0,171 мольных долей, достигается при T = 373 К и tend = 8 ч. Наибольшее значение концентрации бензи-лиденбензиламина, найденное при варьировании концентрации бензиламина и постоянной температуры (tend = 8 ч) составляет 0,176 мольных долей (рис. 5).

Рис. 2. Динамика концентраций веществ: 1 – X7 , 2 – X2 , 3 – X1

Рис. 3. Зависимость концентрации бензилиденбензиламина от начального состава реакционной смеси и времени протекания реакции

Результаты приведенных расчетов показывают, что рассчитанные наибольшие значения концентраций бензилиденбензиламина меньше значения его концентрации, найденного при вычисленных оптимальных значениях управляющих параметров.

Решение задачи (11) – (19) также найдено с помощью метода вариаций в пространстве управлений [15]. В качестве начального приближения решения задачи заданы значения управляющих параметров: T(t) = 329 К, tend = 4 ч, x1 (0) = x2(0) = 0, 5 мольных долей. Задача решена с шагом 0,1 К для температуры, с шагом 0,1 ч для времени реакции и с шагом 0,001 мольных долей для начальных концентраций. Получено наибольшее значение концентрации бензилиденбензиламина, равное 0,335 мольных долей при t*nd = 8 ч и x1 (0) = 0, 676 мольных долей, х2(0) = 0, 324 мольных долей. Структура оптимальной температурной кривой процесса близка к температурному профилю, рассчитанному с помощью алгоритма дифференциальной эволюции. Количество обращений к целевому функционалу при решении задачи с помощью разработанного алгоритма составило 2131, а при использовании метода вариаций – 10232. Поэтому для поиска оптимальных значений параметров реакции получения бензилиденбензиламина целесообразно применять разработанный алгоритм.

Рис. 4. Зависимость концентрации бензилиденбензиламина от температуры реакции и ее продолжительности

Рис. 5. Зависимость концентрации бензилиденбензиламина от начального состава реакционной смеси и температуры реакции

Заключение

Таким образом, разработанный алгоритм позволяет определять оптимальные значения параметров каталитической реакции. Алгоритм сочетает в себе возможность поиска параметров управления, являющихся функцией (температура реакции) и константами (время реакции, оптимальные начальные концентрации веществ). Алгоритм основан на применении метода дифференциальной эволюции и учитывает физико-химические особенности задачи оптимального управления каталитической реакцией. Проведен вычислительный эксперимент для реакции получения бензилиденбензиламина, в результате которого определены температурный режим, продолжительность реакции и набор начальных концентраций реагентов, при которых достигается наибольшая концентрация целевого продукта реакции – бензилиденбензиламина. Сравнение полученных результатов решения оптимизационной задачи с решением, рассчитанным методом вариаций в пространстве управлений, подтверждает корректную работу алгоритма. При этом вычислительные затраты разработанного алгоритма ниже, по сравнению с методом вариаций. Разработанный алгоритм можно применять для каталитических реакций с целью определения стратегии управления процессом, не прибегая к проведению лабораторного эксперимента.

Исследование выполнено за счет гранта Российского научного фонда № 24-21-00186,