Цифровые модемы сигналов минимальной частотной манипуляции и их характеристики

Цифровые модемы сигналов минимальной частотной манипуляции (МЧМ) широко используются в системах сотовой связи стандарта GSM, в системах беспроводной связи стандарта DECT, в системах спутниковой связи и в ряде других систем. На заре своего появления сигналы МЧМ применялись в системах аналоговой сотовой связи стандарта NMT для передачи цифровых сигналов набора номера. Столь широкое применение модемов сигналов МЧМ обусловлено высокой помехоустойчивостью сигналов МЧМ, сравнительно узкой шириной спектра и постоянной амплитудой сигнала. В многочисленной литературе, посвященной описанию сигналов МЧМ [1–9], приводятся сведения об особенностях этого вида модуляции, а также различные варианты схем реализации модемов сигналов МЧМ. В отечественной литературе минимальную частотную модуляцию называют также модуляцией с минимальным сдвигом частоты (ММС), а в англоязычной литературе она получила название MSK (Minimum Shift Keying). Для сужения спектра сигнала МЧМ подлежащие передаче прямоугольные посылки предварительно пропускают через фильтр нижних частот (фильтр Гаусса). Такую разновидность сигнала МЧМ называют гауссовой МЧМ, а в англоязычной литературе она получила аббревиатуру GMSK. С формальной точки зрения название «минимальная частотная манипуляция» некорректное. Принято считать, что частотная манипуляция называется минимальной, если сдвиг частот сигнала fp равен частоте манипуляции Fм = V / 2, где V = = 2Fм – скорость манипуляции, а девиация частоты fд = fp / 2 = Fм / 2. Тогда индекс частотной модуляции, равный отношению девиации частоты сигнала fд к частоте манипуляции Fм, у сигнала МЧМ равен В = fд / Fм = 0,5. Но девиацию частоты сигнала можно сделать меньше Fм / 2. Почему же сигнал МЧМ получил такое название? Ответ на этот вопрос изложен ниже.

[м^^е © Тяжев А.И., 2023

• 1.    Алгоритмы формирования сигналов классической частотной манипуляции и сигналов минимальной частотной манипуляции

Отличие алгоритма формирования сигнала МЧМ от алгоритма формирования классического ортогонального в усиленном смысле сигнала частотной манипуляции (ЧМ) состоит в следующем. У классического ортогонального сигнала частотной манипуляции (ЧМ) за длительность передачи посылки одного знака Т = 1 / V укладывается целое число периодов колебаний синуса или косинуса, а при передаче посылки другого знака за время Т укладывается целое число периодов, отличающееся на единицу. У сигнала МЧМ за длительность Т передачи посылки одного знака укладывается целое число полупериодов колебаний синуса или косинуса, а при передаче посылки другого знака за время Т укладывается целое число полупериодов, отличающееся на единицу. Причем в отличие от фазоманипулированного сигнала, в котором присутствуют скачки фазы, в сигнале МЧМ фаза сигнала при переходе от одной посылки к другой непрерывная. Это означает, что фаза сигнала в начале следующей посылки совпадает с фазой сигнала в конце предыдущей посылки. Поэтому сигнал МЧМ называют также сигналом ЧМ с непрерывной фазой [6; 8]. Покажем, что из-за отличий алгоритмов формирования сигналов ЧМ и МЧМ индекс частотной модуляции у ортогонального сигнала ЧМ равен В = f_д / F_м = 1, а у сигнала МЧМ он равен В = f g /F_M = 0,5. Для этого обозначим буквой f_н нижнюю, а буквой f_в верхнюю частоту сигналов ЧМ и МЧМ, тогда, соответственно, периоды колебаний будут равны

Т н = 1 / f н , Т в = 1 / f в .

Пусть за длительность посылки Т укладывается N_н периодов Т_н = 1 / f_н и N_в = N_н + 1 периодов Т_в = 1 / f_в. Тогда из алгоритма формирования сигнала ЧМ запишем:

T_HN_H = T , T N = T₈ ( N + 1 ) = T .

НН     оо о Н

Приравняем левые части этих выражений и получим: THNH = T8 (NH +1). Перейдем от периодов к частотам: fgNH = fH (NH +1), откуда получим: NH (/о - fH) = fH. Разность частот fв – fн = 2fд = fн / Nн = 1 / (ТнNн) = = 1 / Т = V = 2 Fm , тогда индекс модуляции для классического ортогонального сигнала ЧМ равен В = fд / Fм = 1. Про- ведем аналогичные преобразования для сигнала МЧМ с учетом отличия от ЧМ алгоритма его формирования. Пусть за длительность посылки Т укладывается Nн полупериодов 0,5Тн и Nв = Nн + 1 полупериодов 0,5Тв. Тогда из алгоритма формирования сигнала МЧМ запишем:

0,5 T N = T , 0, 5T N = 0, 5T_s ( N _H + 1 ) = T . H H             о о         о H

Приравняем левые части этих выражений и получим: 0,5THNH = 0,5T8 (NH +1). Умножим это уравнение на 2 и перейдем от периодов к частотам f8Nn = fn (Nn + 1) , откуда получим: NH (/о — fH ) = = fH. Разность частот fв – fн = 2fд = fн / Nн = 1 / (ТнNн) =

= 1 / 2 Т = V / 2 = Fm , тогда индекс модуляции для сигнала МЧМ будет равен В = fд / Fм = 0,5. Разница в приведенных формулах для сигналов ЧМ и МЧМ в том, что для сигнала ЧМ произведение ТнNн = Т, а для сигнала МЧМ ТнNн = 2Т. Отметим, что сигналы МЧМ можно формировать как из отрезков синусоиды, так и из отрезков косинусоиды. В последнем случае изменение частоты сигнала происходит не в моменты перехода сигнала через ноль, а в моменты экстремумов сигнала. Такой сигнал из отрезков косинусоиды приведен на рис. 7. А теперь ответим на вопрос о названии сигнала МЧМ. Несмотря на разные алгоритмы формирования сигналов ЧМ и МЧМ, последний также является ортогональным на интервале длительности посылки Т, т. к. интеграл произведения сигналов от посылок разных знаков x1(t) и x2(t) на интервале длительности посылок Т для сигнала МЧМ также равен нулю:

T

J x 1 ( t ) x 2 ( t )d,t = 0.                                                (1)

При снижении девиации частоты f_д меньше F_м / 2 и, соответственно, индекса модуляции В меньше 0,5 ортогональность сигналов МЧМ нарушается, и указанный выше интеграл (1) будет отличен от нуля. Таким образом, название сигналов МЧМ обусловлено минимальным значением индекса модуляции В = f_д / F_м = 0,5, при котором еще обеспечивается ортогональность сигналов посылок разных знаков x ₁( t ) и x ₂( t ) в сигнале МЧМ на интервале длительности посылки Т . Требуемые временные соотношения при формировании сигнала МЧМ могут быть обеспечены только при цифровой обработке сигналов.

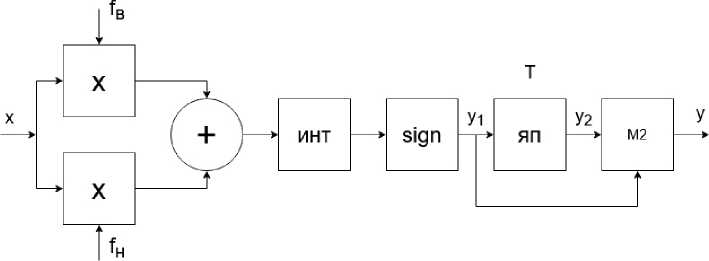
Рис. 1. Структурная схема когерентного демодулятора сигналов МЧМ

Fig. 1. Block diagram of a coherent demodulator of MSK signals

2.    Формирование сигналов МЧМ

Существует несколько способов формирования сигналов МЧМ [8; 9]. Опишем два способа, которые получили названия квадратурный и прямой. При квадратурном способе сигнал МЧМ x ( t ) представим в виде

t x (t) = cos(to0t + 2nJ fdxM (t) dt) = C 0 (t )C (t) - S0 (t) S (t), 0

где to o = 2 п f о , f о = 0,5(f_B + f_H ) — центральная частота сигнала МЧМ, f_д = V / 4 – девиация частоты сигнала МЧМ, х м ( t ) = 1 или х м ( t ) = -1 - модулирующий сигнал, а квадратурные компоненты равны:

Cо(t) = cos toot, Sо(t) = sinto0t, tt

C ( t ) = cos(2 n J f_dx_M ( t ) dt ), S ( t ) = sin(2 n J f_dx_M ( t ) dt ).

Из этих выражений следует, что для формирования сигнала МЧМ квадратурным способом нужны интегратор модулирующего сигнала х_м ( t ), функциональные преобразователи в косинус и синус сигнала на выходе интегратора, косинусно-синусный генератор центральной частоты f ₀ сигнала МЧМ, два перемножителя и сумматор [9]. Сигнал МЧМ, сформированный по описанному выше квадратурному способу, получается в виде отрезков косинусоид. Прямой способ формирования сигнала МЧМ выполняется на базе генератора пилообразных колебаний, частоты f_в и f_н которого задаются коэффициентами А_в и А_н , рассчитанными по формулам:

А_в = 2 f_в / F_д , А_н = 2 f_н / F_д , а сами частоты f_в и f_н рассчитываются из соотношений, следующих из алгоритма формирования сигнала МЧМ при выбранных значениях N_н и N_в = = N_н + 1 . Отсчеты Z ( n ) пилообразных колебаний формируются по формулам:

Z ( n ) = Z ( n – 1) + A при Z ( n – 1) + A < 1;

Z(n) = Z(n – 1) + A – 2 при Z(n – 1) + A > 1, где А = Ав или А = Ан в зависимости от передаваемого сообщения. Затем с помощью функционального преобразования отсчеты пилообразных колебаний преобразуются в отсчеты треугольных колебаний, которые затем пересчитываются в отсчеты гармонических колебаний, например с помощью нечетных полиномов Чебышева первого рода [7]. При этом способе формирования сигнал МЧМ может быть сформирован как из отрезков синусоид, так и из отрезков косинусоид, т. к. цифровые косинусно-синусные генераторы имеют два выхода: синусный и косинусный. Для повышения чистоты спектра сигналов косинусно-синусных генераторов их можно пропустить через рекурсивные цифровые фильтры второго порядка [10].

3.    Когерентный демодулятор сигналов МЧМ

Существует также несколько способов детектирования сигналов МЧМ [1; 2; 8; 9]. Опишем схему когерентного демодулятора сигналов МЧМ с когерентными сигналами x ₁( t ) и x ₂( t ) опорными колебаниями на частотах f_в и f_н . Помехоустойчивость в гауссовом канале у него такая же, как у демодулятора сигналов относительной фазовой манипуляции со скачками фазы сигнала на п [1; 2; 6]. Такую модуляцию называют также модуляцией с противоположными сигналами. Структурная схема когерентного демодулятора сигналов МЧМ приведена на рис. 1.

В состав демодулятора входят генераторы сигналов частот f_в и f_н (на схеме они не показаны), формирующие когерентные с входными сигналами x ₁( t ) и x ₂( t ) колебания. Кроме того, в состав схемы демодулятора входят два перемножителя, сумматор, интегратор, блок sign, ячейка памяти (ЯП) и узел сложения по модулю два (М2) на выходе. На рис. 2 приведены временные диаграммы, поясня-

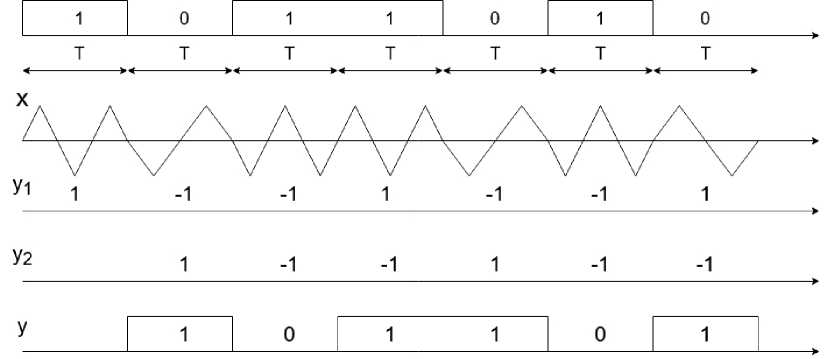
Рис. 2. Временные диаграммы, поясняющие работу демодулятора сигнала МЧМ с числами полупериодов N_н = 2 и N_в = 3

Fig. 2. Timing diagrams explaining the operation of the MSK signal demodulator with the numbers of half-cycles N_н = 2 and N_в = 3

ющие работу изображенного на рис. 1 демодулятора сигнала МЧМ с числами полупериодов N_н = = 2 и N_в = 3.

На первой верхней диаграмме показана подлежащая передаче последовательность посылок 1 0 1 1 0 1 0 длительностью Т каждая. На передающей стороне в модуляторе посылке 1 ставится в соответствие модулирующий сигнал хм(t) = 1, а посылке 0 – модулирующий сигнал хм(t) = –1. На второй диаграмме показан сформированный в соответствии с этой последовательностью посылок сигнал МЧМ из отрезков синусоид. Для простоты графического исполнения вместо синусоиды изображены треугольные сигналы, что не влияет на принцип работы демодулятора сигналов МЧМ. Из второй диаграммы рис. 2 видно, что при передаче посылки 0 число полупериодов синусного сигнала Nн = = 2, а при передаче посылки 1 число полупериодов синусного сигнала Nв = 3. Из этой же диаграммы видно, что фаза сигнала непрерывная. Благодаря этому начальная фаза сигналов x1(t) и x2(t) на интервале посылки Т может принимать значения 0 или п. Таким образом, модуляция в сигнале МЧМ по природе соответствует модуляции с противоположными сигналами. В результате в сигнале МЧМ может быть четыре варианта передаваемого сигнала: два варианта с разными частотами fв и fн и два варианта с разными начальными фазами 0 или π на интервале посылки Т. Как видно из рис. 1, входной сигнал поступает на два перемно-жителя, на вторые входы которых поступают когерентные с сигналами x1(t) и x2(t) колебания частот fв и fн, причем на верхний перемножитель поступает колебание синуса с частотой fв, а на нижний перемножитель – колебание синуса с частотой fн. Если включить на выходы этих перемножителей два интегратора, то в соответствии с формулой (1) на выходе интегратора перемножителя сигналов с несовпадающими частотами сигнал в конце посылки будет равен нулю. А на выходе интегратора перемножителя сигналов с совпадающими частотами сигнал в конце посылки будет положительным или отрицательным в зависимости от того, с какой начальной фазой 0 или π поступил входной сигнал х. Из сказанного следует, что на выходе одного из интеграторов сигнал в конце посылки будет равен нулю. Принимая это во внимание, а также то, что интеграл суммы равен сумме интегралов, в схеме демодулятора можно вместо двух интеграторов оставить один интегратор и включить его на выходе сумматора сигналов с выходов перемножителей, как это сделано на рис. 1. На выходе интегратора включен блок sign, формирующий сигнал у1 по следующему алгоритму: если на входе блока sign сигнал в конце посылки положительный, то у1 = 1, если на входе блока sign сигнал в конце посылки отрицательный, то сигнал у1 = –1. Поясним, как формируется сигнал у1, приведенный на третьей диаграмме. Сигнал от первой посылки с частотой fв поступает с начальной фазой, равной нулю. Опорные колебания всегда формируются с начальной фазой, равной нулю, поэтому в конце приема первой посылки на выходе интегратора сигнал будет положительный и сигнал у1 = 1. При передаче второй посылки сигнал х на частоте fH имеет начальную фазу п, поэтому сигнал на выходе верхнего интегратора в конце второй посылки будет отрицательным, следовательно, у1 = –1. При передаче третьей посылки сигнал х на частоте fe имеет начальную фазу п, поэтому сигнал на выходе интегратора в конце третьей посылки также будет отрицательным, следовательно,

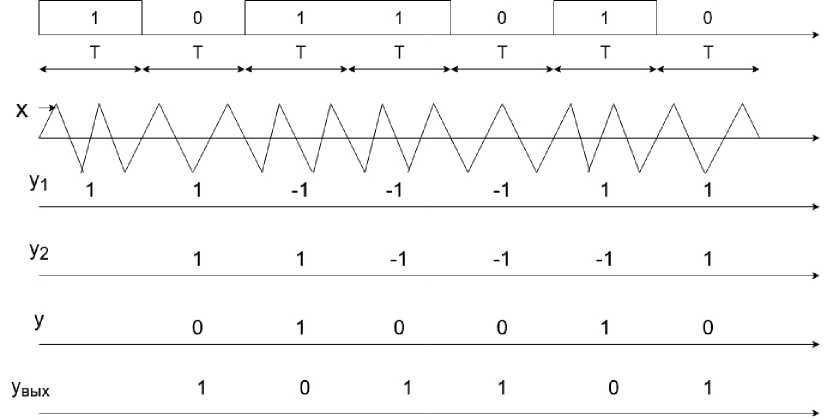
Рис. 3. Временные диаграммы, поясняющие работу демодулятора сигнала МЧМ с числами полупериодов N_н = 3 и N_в = 4

Fig. 3. Timing diagrams explaining the operation of the MSK signal demodulator with the numbers of half-cycles N_н = 3 and N_в = 4

у ₁ = –1. А при передаче четвертой посылки сигнал х на частоте f_в имеет начальную фазу 0, поэтому сигнал на выходе интегратора в конце четвертой посылки также будет положительным, следовательно, у ₁ = 1. Аналогичный анализ проведем для остальных посылок и получим приведенные на третьей диаграмме сигналы у ₁. На четвертой диаграмме приведен сигнал у ₂, это задержанный с помощью ячейки памяти на время длительности посылки Т сигнал у ₁. Выходной сигнал у формируется из сигналов у ₁ и у ₂ в узле сложения по модулю два по правилу: если сигналы у ₁ и у ₂ одинаковые, то у = 0, если сигналы у ₁ и у ₂ разные, то у = 1. Сформированный по этому правилу сигнал у приведен на пятой диаграмме. Сравнение этого сигнала с передаваемым сигналом показывает, что принятый сигнал у совпадает с передаваемым сигналом, приведенным на первой диаграмме. На рис. 3 построены временные диаграммы, поясняющие работу изображенного на рис. 1 демодулятора сигнала МЧМ с числами полупериодов N_н = 3 и N_в = 4 и с такой же последовательностью передаваемых посылок, как на рис. 2.

Формирование сигналов у1, у2 и у на рис. 3 происходит так же, как описано выше для рис. 2. Однако сигнал у на рис. 3 является инвертированным по отношению к передаваемым посылкам. Чтобы воспроизвести передаваемые посылки, пропустим сигнал у через инвертор и получим сигнал увых, совпадающий с передаваемыми посылками. Таким образом, при четных числах Nн инвертор на выходе демодулятора на рис. 1 не нужен, а при нечетных числах Nн надо включать инвертор на выходе. Отметим также, что в генераторе с четным числом Nн или Nв фаза колебаний в начале каждой посылки равна нулю, а в генераторе с нечетным числом Nн или Nв она чередуется и равна либо нулю, либо π. Чтобы обеспечить начальную фазу колебаний этого генератора равной нулю в начале поступления сигнала каждой посылки, надо предварительно перемножить колебание генератора на меандр с длительностью посылок Т с чередующимися значениями +1 и –1. Если для детектирования сигналов МЧМ применять другие частотные детекторы, не учитывающие начальные фазы сигналов x1(t) и x2(t), то помехоустойчивость у этих детекторов будет хуже, чем у когерентного демодулятора сигала МЧМ. Но в этом демодуляторе схема сложнее, т. к. в ней надо обеспечить синхронность и синфазность колебаний генераторов с сигналами x1(t) и x2(t).

4.    Автокорреляционный демодулятор сигналов МЧМ с бинарным квантованием сигнала

Ниже приведены схема и описание работы наиболее простого в реализации цифрового демодулятора сигналов МЧМ, в котором вместо аналогоцифрового преобразователя на входе включен ограничитель сигнала ОГР [2]. За счет ограничителя происходит бинарное квантование входного сигнала х по алгоритму: если х > 0 или х = 0, то выходной сигнал ограничителя у ₁ = 1, если х < 0, то у ₁ = 0. На рис. 4. приведена структурная схема автокорреляционного демодулятора сигналов МЧМ с бинарным квантованием сигнала. Помехоустой-

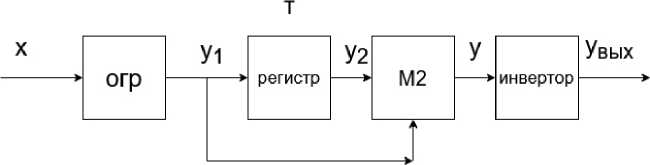
Рис. 4. Структурная схема автокорреляционного демодулятора сигналов МЧМ с бинарным квантованием сигнала

Fig. 4. Block diagram of an autocorrelation demodulator for MSK signals with binary quantization of the signal

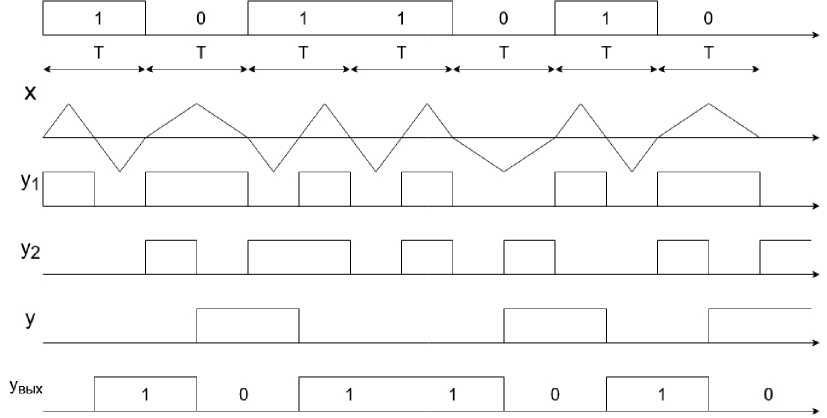
Рис. 5. Временные диаграммы, поясняющие работу демодулятора сигнала МЧМ с бинарным квантованием сигнала при N_н = 1, N_в = 2

Fig. 5. Timing diagrams explaining the operation of the MSK signal demodulator with binary quantization of the signal at N_н = 1, N_в = 2

чивость у этого демодулятора такая же, как у автокорреляционного демодулятора сигналов ФРМ.

В состав схемы демодулятора входит ограничитель на входе, последовательный регистр, задерживающий входной цифровой сигнал у ₁ на длительность посылки Т , узел сложения по модулю 2 и инвертор на выходе. В [2] показано, что в этом демодуляторе при изменении частоты входного сигнала смена знака сигнала на выходе узла М2 сопровождается дроблениями. Длительность импульсов дробления изменяется на величину 0,5( Т_н – Т_в ) по арифметической прогрессии, а число этих импульсов равно m₁ = f_н / f_p . Суммарная длительность импульсов дробления равна:

Тс = 0,5(Тн – Тв)(m2 – 1)m2 / 2,(2)

где m ₂ = 0,5 m ₁ при четном m ₁, m ₂ = 0,5( m ₁ – 1) при нечетном m₁ . Перейдем в (2) от периодов к частотам и получим:

Т _ ^н—Л_ при нечетном m •(3)

с 16 Up

Т _ —Zh_ при четном m .(4)

С   16 fefp

Из формулы (3) следует важный вывод, что при выполнении условия fв = 2fн величина Тс = 0. Сле- довательно, при выполнении указанного условия дробления посылок на выходе узла М2 при изменении частоты сигнала отсутствуют, благодаря чему обеспечивается наилучшая помехоустойчивость сигнала МЧМ в демодуляторе на рис. 4. Из условия fв = 2fн вытекают следующие соотношения для сигнала МЧМ:

Т_в = Т , Т_н = 2 Т , N_н = 1, N_в = 2. (5)

На рис. 5 приведены временные диаграммы, поясняющие работу демодулятора сигнала МЧМ с бинарным квантованием сигнала, причем сигнал МЧМ удовлетворяет приведенным выше условиям и соотношениям (5).

На верхней диаграмме приведены подлежащие передаче посылки 1 0 1 1 0 1 0 длительностью Т . На второй диаграмме приведен сигнал МЧМ х , сформированный из отрезков синусоид, причем при передаче 1 за время Т укладывается 2 полупериода синусоиды с частотой f_в , а при передаче 0 за время Т укладывается 1 полупериод синусоиды с частотой f_н , при этом фаза сигнала х непрерывная. На третьей диаграмме приведен сигнал на выходе ограничителя у ₁, сформированный в соответствии с алгоритмом работы ограничителя. На четвертой диаграмме приведен сигнал у ₂ на вы-

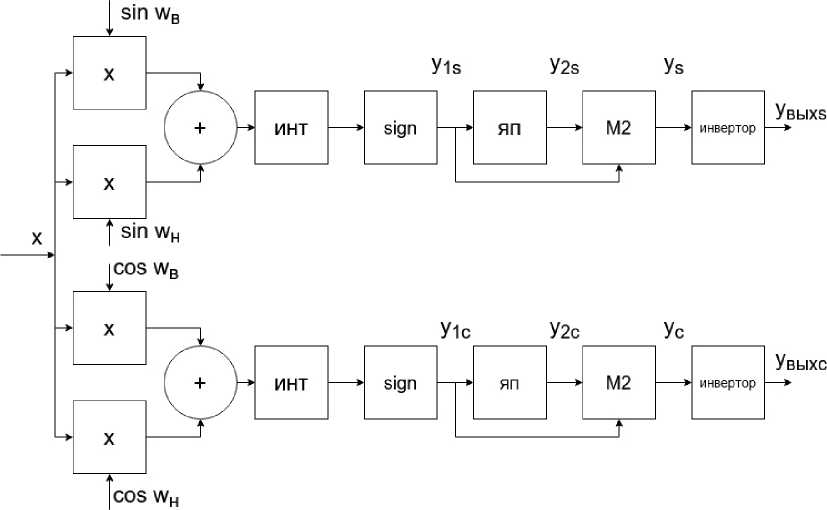
Рис. 6. Структурная схема двухканального демодулятора сигналов МЧМ

Fig. 6. Block diagram of a two-channel MSK signal demodulator

ходе регистра, это задержанный на время Т сигнал у ₁. Если сложить сигналы у ₁ и у ₂ по модулю 2, то получим сигнал у на выходе узла М2. Сигнал у является инверсией передаваемых посылок, т. к. число N_н = 1 нечетное. На шестой диаграмме приведен выходной сигнал демодулятора у _вых, являющийся инверсией сигнала у . Сравнивая сигналы на первой и шестой диаграммах, убеждаемся, что выходной сигнал демодулятора у _вых совпадает с передаваемыми посылками. Сформировать сигнал МЧМ из отрезков синусоиды или косинусоиды с числами N_н = 1, N_в = 2 цифровым способом не представляет трудности. Затем с помощью гетеродина и преобразователя частоты этот сигнал переносится в диапазон высоких частот для передачи по радиоканалу. На приемной стороне с помощью преобразователя и гетеродина частоту сигнала снова приводят в первоначальное значение. При этом условие f_в = 2 f_н служит критерием для обеспечения синхронизации частоты гетеродина в преобразователе приемника.

5.    Двухканальный модем сигналов МЧМ

Выше было отмечено, что для формирования сигнала МЧМ можно использовать как отрезки полупериодов синусоиды, так и отрезки полупериодов косинусоиды. Но сами функции синусоиды и косинусоиды одного аргумента на отрезке полупериода являются ортогональными. Это об- стоятельство позволяет создать двухканальный модем сигналов МЧМ, способный передавать две независимые последовательности посылок со скоростью передачи V = 1 / Т каждая, при этом ширина спектра такого двухканального сигнала МЧМ не расширятся, а остается такой же, как у одноканального сигнала МЧМ. Таким образом, в двухканальном модеме сигналов МЧМ спектральная эффективность в два раза выше, чем у одноканального модема сигналов МЧМ. Построение двухканального модулятора сигнала МЧМ тривиально, поэтому здесь не описывается. На рис. 6 приведена структурная схема двухканального демодулятора сигнала МЧМ, а на рис. 7 приведены временные диаграммы, поясняющие работу двухканального демодулятора сигналов МЧМ с числами полупериодов Nн = 1, Nв = 2.

В схеме двухканального демодулятора на рис. 6 оба канала идентичны. Отличие состоит только в том, что на вторые входы перемножителей в верхнем канале поступают колебания синуса частот to ₆ = 2 n f_s и to _н = 2 n f_H , а на вторые входы перемно-жителей в нижнем канале поступают колебания косисинуса частот to _s = 2 п f_e и to _в = 2 п f_H .

Так как функции синуса и косинуса одного аргумента ортогональны на интервале полупериода, они будут ортогональны и на интервале длительности посылки Т , потому что на этом интервале укладывается целое число полупериодов N_н и N_в . Для простоты и наглядности на рис. 7 изображе-

10 10  1

	1	1	1	0	0
Хс'
У1з	1	1	-1	-1	1
У2з		1	1	-1	-1           .
Уз		0	1	0	1
Увыхз		1	0	1	0
У1с	1	1	1	1	-1
У2с		1	1	1	1
Ус		0	0	0	1
/выхс		1	1	1	0

Рис. 7. Временные диаграммы, поясняющие работу двухканального демодулятора сигналов МЧМ с числами полупериодов N_н = 1, N_в = 2

Fig. 7. Timing diagrams explaining the operation of a two-channel demodulator of MSK signals with numbers of half-cycles N_н = 1, N_в = 2

ны сигналы МЧМ с числами полупериодов N_н = 1, N_в = 2, хотя эти числа могут быть и другими. На верхней диаграмме приведены посылки 10101 для передачи по каналу синуса, а на второй диаграмме изображен соответствующий этим посылкам сигнал МЧМ х_s из отрезков синусоиды. На третьей диаграмме приведены посылки 1 1 1 0 0 для передачи по каналу косинуса, а на четвертой диаграмме изображен соответствующий этим посылкам сигнал МЧМ х_с из отрезков косинусоиды. На вход демодулятора на рис. 6 поступает суммарный сигнал х = х_s + х_с . Но в силу ортогональности функций синуса и косинуса сигнал х_с не влияет на работу верхнего канала, а сигнал х_s не влияет на работу нижнего канала, т. к. интеграл (6) равен нулю:

T

J x s ( t ) x c ( t)dt = 0. (6) 0

Поэтому приведенные на рис. 7 сигналы синусного канала у _{1 s} , у _{2 s} , у_s и у _{вых s} формируются так же, как и сигналы у ₁, у ₂, у и у _вых на рис. 3. Приведенные на рис. 7 сигналы косинусного канала у _{1 с} , у _{2 с} , у_с и у _{вых с} формируются так же, как и сигналы у ₁, у ₂, у и у _вых на рис. 3, с той лишь разницей, что на вторые входы перемножителей этого канала поступают колебания косинуса частот co , = 2 п f_e и to _^ = 2 п f_^ .

Сопоставляя сигналы у _{вых s} и у _{вых с} с передаваемыми посылками по каналам синуса и косинуса, убеждаемся, что принятые по этим каналам посылки совпадают с передаваемыми посылками.

Заключение

У описанных модемов сигналов МЧМ помехоустойчивость в гауссовом канале такая же, как у демодулятора сигналов относительной фазовой манипуляции (ОФМ) со скачками фазы сигнала на π [1; 2; 6]. Но у сигналов МЧМ есть еще два преимущества по сравнению с сигналами ОФМ – это постоянная амплитуда и меньшая ширина спектра, благодаря чему сигналы МЧМ практически вытеснили сигналы ОФМ из аппаратуры связи. У двухканального модема сигналов МЧМ спектральная эффективность в два раза выше, чем у одноканального модема сигналов МЧМ. Работа этого модема сходна с работой модема сигналов OFDM [11; 12]. Как и в модеме сигнала OFDM, суммарный сигнал двухканального модема х = х_s + х_с не является сигналом с постоянной амплитудой, это может создать некоторые проблемы в работе передающей части модемов двухканальных сигналов МЧМ.