Цилиндрический проводник в слое изотропной плазмы

Вокруг летательного аппарата, движущегося в атмосфере, образуется слой изотропной плазмы. Направленно перемещающийся объект будем аппроксимировать проводящим телом цилиндрической геометрии – проводящим цилиндром. На цилиндр, находящийся в слое плазмы, наводятся токи – цилиндр становится направляющей электродинамической структурой.

В общем случае электромагнитное поле, связанное с проводящим цилиндром (с проводником, при малых радиусах цилиндра), описывается несамосопряженной краевой задачей. Несамосо-пряженность при использовании импедансного метода [1] обуславливается неэквивалентностью граничных условий прямой и сопряженной краевых задач. В общем случае собственные значения несамосопряженных краевых задач являются [2–5] комплексными величинами, что определяет комплексность волновых чисел. В связи с этим исключительно важен вопрос классификации волн направляющей структуры рассматриваемого типа.

Исследованию особенностей распространения электромагнитных полей вдоль импедансных поверхностей посвящено достаточно много работ [6–12]. Однако, несмотря на относительную простоту краевых задач, описывающих электромагнитные процессы в импедансных структурах с гладкими границами, полной ясности в их (процессов) понимании нет. В частности, несмотря на многократные обсуждения, так и нет ясности в отношении существования волны Ценнека [1].

Основным недостатком всех дискуссий по поводу особенностей распространения волн вдоль импедансных поверхностей было то, что они, как правило, проводились на уровне двумерных плоских краевых задач без учета специфики не-самосопряженности соответствующих им операторов. В статье рассматривается трехмерная задача о распространении электромагнитных полей вдоль импедансного цилиндра, окруженного слоем изотропной плазмы. При понижении электронной концентрации плазмы можно осуществить предельный переход к однопроводной линии в неограниченной изотропной среде.

1. Постановка дисперсионной задачи

Рассматриваем направляющую структуру в виде проводящего цилиндра, окруженного слоем изотропной плазмы. Ее поперечное сечение показано на рис. 1.

Область I – проводящий цилиндр, выполненный из материала с диэлектрической проницаемостью

ε1 =ε′ + iε′′ =ε′ -iσ ,                                (1)

ω область II – слой изотропной плазмы с относительной диэлектрической проницаемостью l = 52 = 1 -^p ,                              (2)

ε0 ω где ωp – ленгмюровская частота, вычисляемая как

ω _p = 4 π Ne ² m ,                             (3)

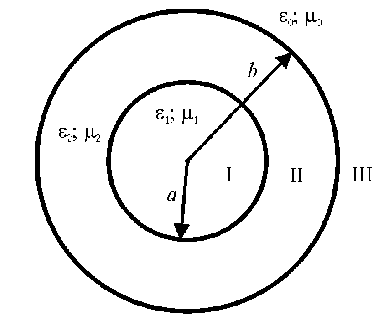
Рис. 1. Поперечное сечение рассматриваемой электродинамической структуры

N – концентрация электронов; e и m – заряд и масса электрона; магнитная проницаемость во всех областях — Цо.

Поле во всех выделенных областях, рис. 1, описывается в общем случае обоими векторами

Герца, продольные компоненты которых удов- летворяют уравнению Гельмгольца д2п I- m д r r

1 дп zm ₊ _1_ д ² П I m r д r     r ² дф ²

2 e , m

+ д П!  + ецю2пe,m = 0, д 22

где r , ф , г — цилиндрические координаты.

Во внутренней области I, рис. 1, поле существует только вблизи границы r =а и учитывается граничным условием Щукина-Леонтовича [13]. Поэтому решения уравнения (4) записыва- ются в виде:

п ii = п m = о,

| ^п 1 2 = [ AJ n ( ^а 2 ^r ) ⁺ AY n ( ^а 2 ^r ) ] cos ⁿ Ф e — i ³² ;

[п m = [ BJ n ( « 2 r ) + BY n ( « 2 r ) ] sin n Ф e~ i ^{3 z} ;

[п 1 3 = CH² ( « 3 r ) cos n Ф e ^- i ^{e z} ;

[п m = DH n2 ( а з r ) sin n ф e ^- i ^{p z} ;

где P — продольное волновое число;

^а 2,3 = ^^е 2,3 ^Ц 0 ^ю 2 - Р 2

– поперечные волновые числа в областях II, III; S 3 = Е о ; J_n ( а 2 r ) и Y_n ( а 2 r ) — цилиндрические функции 1-го и 2-го рода.

Поля в рассматриваемой направляющей структуре удовлетворяют граничным условиям:

E ф 2 ( ^r = a )/ H z 2 ( ^r = a ) = ^W ;

EI2 ( r = a )/HФ2 ( r = a ) = -W, где W – волновое сопротивление материала проводящего цилиндра;

E z 2 ^{( r} = b ) = E z 3 ^{( r} = b ) ; H z 2 ^{( r} = b ) = H z 3 ^{( r} = b ) ; E ф 2 ( ^r = b ) = E ф з ( ^r = b ) ; H ф 2 ( ^r = b ) = H ф 3 ( ^r = b ) .

Уравнение (4) с граничными условиями Щукина-Леонтовича (6) и условиями непрерывности тангенциальных компонент поля (7), (8) на границах раздела сред образуют несамосопряженную краевую задачу [2–4], собственные значения которой в общем случае являются [5] комплексными величинами. Граничное условие при r ^ » полагаем незаданным, соответствующим как собственным, так и несобственным волнам.

Из граничных условий (6), выразив компоненты поля через векторы Герца (5), получаем уравнение

i I a [AJn (а2a) + AYn (а2a)^ +

+ юц2а2 [BJn (а2a) + BYn (а2a)] j =           (9)

= а2 [BJn (а2a) + BYn (а2a)] w;

а2 [AJn (а2a) + AYn (а2a)] W =

= i I^n [BJn (а2a) + BYn (а2a)] +            (10)

+ toS2a2 [AJn (a2a) + AYn (а2a)] j;

Из граничных условий (7) получаем:

a2 [AJn (а2b) + AYn (а2b)] = а3СнП2) (азb); (11)

а 2 [ BJ n ( а 2 b ) + BY n ( а 2 b ) ] = а 3 DH n ²⁾ ( а з b ) ; (12)

Вводя обозначения:

P (а2, а3 ) = Jn (а2b)/Hn2^ (а3b) ;

Q (а2, а3 ) = Yn (а2b)/нП2^ (а3b);

из уравнения (11), (12) получаем:

C = at [AP (а2, аз) + AQ ^ аз)];

D = "^1"[BP (а2, аз) + BQ (а2, аз)].

а ² ₃

Граничные условия (8) приводят к уравнениям:

AJn (а2b) + AYn (а2b) =

---/^ 2 x |Цз ^2 [BP (а2, аз )

^E n 1 -o i ^[   “ ³

V аз у

+

⁺ BQ ( « 2 , « 3 ) J H n ( « 3 b ) ^-

- Ц 2 [ BJ ; ( « 2 b ) + BY ; ( « 2 b ) J I ;

BJ n ( « 2 b ) + BY n ( « 2 b ) =

= /^ 2 x le3 — [AP («2, «3 ) + b i-|1 «3

V « 3 7

+ AQ ( ^a 2 , 0. 3 ) J H^ ( « 3 b ) -

^{- e} 2 [ AJ n ( « 2 b ) + AY n ( « 2 b ) J | ;

Обозначив « 2 а = х , из уравнения (9) получаем:

AJ n ( ^x ) ⁺ AY n ( ^x ) =

= - i « n [ BJ n ( x ) + BY n ( x ) J W -

-^ x [ BJ n ( x ) + BY n ( x ) J .

Учитывая, что в представлениях полей все производные от цилиндрических функций изначально берутся по радиальной координате, дифференцируем (17) по х , получаем:

AJ n ( x ) + AY ; ’ ( x ) =

= - i « n [ BJ n ( x ) + BY n ( x ) J W -

- 1- [ BJ n ( x ) + by ; ( x ) ] ( ЮЦ 2 + i « 2 Wx ) в n

-

^ro n x [ bj ; ( x ) + BY n ( x ) J .

Подставляем (17) и (18) в уравнение (10):

[BJn (x) + BYn (x)] X f ГО£2       . вn )

X I ² W + i— I W + i —2— W -

V p n      « 2 x Jв

• -[ BJn( x)+ BYn( x )]x(19)

• x ^^2. - i ^гое 2 (_Ю ц + i « xW ) W -

• V вn     вn«2 v 22 v

• - i ^ 2^2. x [ bj• ( x ) + BY ‘ ( x ) 1 W = 0.

« ₂ в n ^{[ nV} ’ ⁿ

Обозначив « 2 b = y, перепишем уравнение (15) в виде

AJn ( У) + AYn ( У )      "y 2T X в n 1 -S

V « 3 7

-Ц 2 [ BJ n ( У ) + BY n ( У ) J

Опять учитывая, что в представлении полей все производные изначально берутся по радиальной координате, уравнение (20) дифферен- цируем по у, получаем:

AJn (y) + AYn(У)=    .Юy 2. x в n 1 "«2

V « 3 J

^X i^ 3

« 2 [ BP' ( y , « 3 ) + BQ' ( y , « 3 ) ] H n ²' ( « 3 b )

-

• -Ц 2 [ BJ n ( У ) + BY n ( У ) ][+    _Г ^Ю ₂ X X (21)

^в n ¹ -« 2

V   « 3 7

^X 1^ 3 ° ² [ BP ( У , « 3 ) ⁺ BQ ( У , « 3 ) ] ^Hn2 ( « 3 ^b ) ^-

I « 3

• -Ц 2 [ BJ n ( У ) + BY n ( У ) ]} .

Введем обозначения:

[гое         в n |      « x

E i ( x ) = W I —² W + i— — I + iW — ;

V в n      « 2 x 7      в n

П 1 ( x ) = i

^е 2 ^ 2

« 2 в П

го x ;

Z 1 ( x ^-^ - i ^ 2- ( ГОЦ 2 + i « 2 xW ) W ; в n    в n « 2

f

У ( « 2 > « 3 ) = в П 1-V

E 2 ( У

Y ( ^a 2 ^, « 3 )

-

«2 .

« 3 7

;

X

^X ц з « 2- P ' ( y , « з ) ^НП ²⁾ ( « 3 ^b ) ^- ^ 2 ^Jnn ( у ) ;

[   «3

го e₂ y

Z2 (У) =

Y ( « 2 , « 3 )

^X Ц 3 « 2- P ( y , « 3 ) ^НП ²^ ( « 3 ^b ) ^- ^ 2 J n ( у ) ;

_   «3

П 2 ( У )=- ^ГО^ « 2 X

у ( « 2 , « 3 ) « 3

X Ц3«2-P(У,«3)Hn2^ («3b)-Ц2Jn(У) [«

_X H n ²^ (« 3 ^b ) .

H n ²^ (« 3 ^b )

X

о 8о y

§3 (У) =x

Y ( ^a 2 , « 3 )

x Ц 3 «- Q ' ( y, « 3 ) H n ( « 3 b ) ^— Ц 2 Yn ( У ) ;

L   «3

Z3 ( У ) =^^ X

Y ( « 2 > « 3 )

^x Ц 3 — Q ( y, « 3 ) H^ ( « 3 b ) ^— Ц 2 Y n ( у ) ;

L   «3

H n ²⁾ (« 3 b ) H^ ( « 3 b )

a ₁

a ₂

k ₁

= x n ( « 3 b ) ;

_N     ° ^{2 8} 2 У _;

² Y ( a 2 , « 3 )

_Ц2 « 2    ° ^{2 8} 3 У   _;

² « 3 Y ( « 2 > « 3 )

= Ц « 2   ° ^{2 8} 2 У _;

« 3 Y ( a 2 , « 3 )

о 89 y  «?

^{n 3 ( y ,=}7м « 3 ^x

x

Ц 3 ° ²- Q ( У^, « 3 ) H² ( « 3 b ) ^- Ц 2 Y n ( У )

x

H P ( « 3 b ) H² ( « 3 b )

Тогда уравнение (19) перепишется как

B L J n ( x ) § 1 ( x ) ^- J n ( x ) ^z i ( x ) — — J n ( x ) n i ( x ) J + B L Y n ( x ) § 1 ( x ) — ^- Y n ( x ) ^z i ( x ) ^- Y n ( x ) n i ( x ) J = 0.

Уравнение (16) с учетом (20), (21) и введенных выше обозначений запишется в виде

B Ly ( « 2 , « 3 ) J n ( У ) ⁺ § 2 ( У ) У ' ^z 2 ( У ) ^-

^— П 2 ( У ) У J + B Ly ( « 2 > « 3 ) Y n ( У ) ^{+               (23)}

⁺ § 3 ( У ) У ^{+ z} 3 ( У ) ^- П 3 ( У ) У J = 0.

Уравнения (22), (23) образуют систему двух линейных уравнений относительно коэффициентов В и B . Приравнивая нулю главный определитель этой системы, получаем дисперсионное уравнение волн рассматриваемой направляющей структуры:

L J n ( x ) § 1 ( x ) — J n ( x ) ^z i ( x ) ^-

— J n ( x ) П 1 ( x ) J Ly ( « 2 , « 3 ) Y n ( У ) ⁺

⁺ § 3 ( У ) У ^{+ z} 3 ( У ) ^- П з ( У ) У J ^-

—L Y n ( x ) § 1 ( x ) — Y n ( x ) ^z 1 ( x ) —

^- Y n ( x ) П 1 ( x ) J ^L Y ( « 2 , « 3 ) J n ( У ) ⁺

⁺ § 2 ( У ) У ^{+ z} 2 ( У ) ^- П 2 ( У ) У J = 0.

Уравнение (24) решается совместно с ниями, связывающими волновые числа:

⁸ 2,3 ^ 2,3 ° ² = « ² ,3 ⁺ P ²

относительно « 2 , « 3 , в на комплексных стях этих волновых чисел.

Введя обозначения:

уравне-

(25) плоско-

_Цз « 2    ° ^{2 8} 3 У  _;

« 3 Y ( a 2 , « 3 )

P n ( x ) = J n ( x ) § 1 ( x )

^- J n ( x ) ^Z 1 ( x ) ^- J n ( x ) n ( x ) ;

q n ( x ) = Y n ( x ) § 1 ( x ) ^-

^- Yn ( x ) ^Z 1 ( x ) ^- Yn ( x ) П 1 ( x ) .

^c 1 n ( x , у ) = k 2 L q n ( x ) J n ( у ) ^- P n ( x ) Y n ( у ) ^J ;

^c2 n ( x, У ) =

= P n ( x ) { ^k 1 L Y n ( у ) ⁺ Y n ( у ) J + a 2 Y n ( у ) } ^-

• ^-    q n ( x ) { ^k 1 L J n ( у ) ⁺ J n ( у ) J ⁺ a 2 J n ( у ) } ;

c 3 n ( x , у ) =

= P n ( x ) { y ( « 2 , « 3 ) Y n ( у ) ^- a 1 L Y n ( у ) + Y n ( у ) J } ^-

• ^-    q n ( x ) { y ( « 2 , « 3 ) ^- a 1 L J n ( у ) + J n ( у ) J } ,

разрешаем уравнение (24) относительно функции x _n ( « 3 b ). Получаем:

X n ( « 3 ^b ) =

^{- c} 2 n ( x , У ) ± V c ² n ( x , У ) ^{- 4} c 1 n ( x , У ) ^c 3 n ( x , У ) ⁽²⁶⁾

^{2 c} 1 n ( x , У )

При условии

|« 3 b | >>  1, (27) выполняющемся в случае, когда проводящий цилиндр помещен в неограниченную плазменную среду или находится в толстом слое изотропной плазмы, имеем:

X n ( « 3 b ) * - i « 3 . (28)

Наличие в дисперсионном уравнении (26) двух знаков перед радикалом говорит о существовании двух ветвей решений, соответствующих волнам HE _nm и EH _nm . Установим соответствие уравнений (26) указанным типам волн.

Поскольку краевая задача, описывающая рассмотренную структуру, несамосопряженная и не содержит нулевого граничного условия на бесконечности ( r ^ » ), в ней (структуре)

могут существовать как собственные, так и несобственные волны. Первые имеют убывающее по r поле, вторые – нарастающее. Первым волнам соответствует I m а з <  0, вторым I m « 3 >  0, где ^а з = У з + i 8 3 . Полагая, что волна EH nm более высокого порядка по сравнению с волной HE _nm , можно наложить условие

8 3 (HE nm ) >8 3 (EH nm ).

Тогда, используя это условие, можно установить соответствие уравнений (26) двум видам волн: HE _nm и EH _nm в предположении, что вдоль направляющей структуры могут распространяться как собственные, так и несобственные волны

Собственные волны ( 8 3 <  0)

• 1.    C n ( x , y ) >  0; Re x n ( « 3 b ) <  0

• 2.    C n ( x , y ) <  0; Re x n ( « 3 b ) <  0

Если C 2 _n ( x , y ) >  0, б о льшим значением 8 3 в (26) соответствует знак (–) перед радикалом, меньшим – знак (+). Следовательно, в этом случае знак (–) перед радикалом соответствует волне HE _nm , знак (+) – волне EH _nm .

Если C 2 _n ( x , y ) <  0, б о льшим значением 8 3 соответствует знак (+) перед радикалом. Следовательно, в этом случае знак (+) перед радикалом соответствует волне HE _nm , знак (–) – волне EH ™ nm .

Несобственные волны ( 8 3 >  0)

• 1.    C i n ( x , y ) <  0; Re x n ( « 3 b ) >  0

• 2.    ^C i n ^{( x} , y ) >  0; ^Re X n ⁽ « 3 b ) >  ⁰

• 2.    Численные результаты

Если C 2 _n ( x , y ) >  0, (—) перед радикалом соответствует волне HE _nm , знак (+) – волне EH _nm .

Если C 2 _n ( x , y ) <  0, знак (+) перед радикалом соответствует волне HE _nm , знак (–) – волне EH _nm .

Численные исследования проводились при £ 3 = £ 2 , A = - iA , B = - iB, то есть для проводящего цилиндра в неограниченной изотропной плазме. В связи с использованием приближенных граничных условий (6) формулировка краевой задачи для симметричных волн является приближенной и ее (краевую задачу) следует трактовать как квази-самосопряженную: в ней выполняются оба условия самосопряженности [2–4], но при этом косвенно (через граничные условия) учитываются потери в проводящем цилиндре. Поэтому волновые числа симметричных волн, получаемые из дисперсионных уравнений,

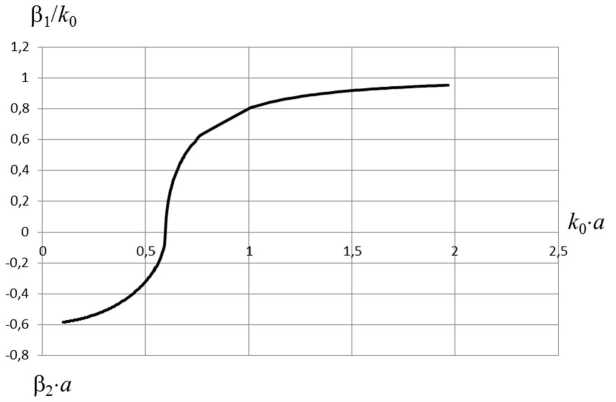
Рис. 2. Дисперсионная характеристика и характеристика затухания симметричной волны для следующих параметров структуры: радиус металлического стержня а = 0,3 м; проводимость металла ст = 56 • 10 6 См/м; концентрация электро-

24 — 3

нов плазмы N = 1 • 10 м должны быть «слабо комплексными». Квази-самосопряженность симметричных краевых задач должна приводить к исчезающе малой комплексности волновых чисел. Последние в силу формальной самосопряженности симметричных краевых задач должны быть либо чисто действительными, либо чисто мнимыми величинами.

Что касается несимметричных (гибридных) волн, то описывающие их краевые задачи в используемой формулировке являются строго несамосопряженными. Поэтому их собственные значения в общем случае являются комплексными величинами [5].

Симметричные волны

Общее дисперсионное уравнение (24) в рассматриваемом случае для симметричных волн распадается на два уравнения:

а H ² ( а a ) — i ю£ 2 WHn^’ ( а a ) = 0 (29) для волн E_{0 m} и

W а H ² ( а a ) — i wp ₂ H n ² ( а a ) = 0 (30) для волн H q m . В (29), (30) обозначено а = а 2 .

Идентификация уравнений (29), (30) производится на основе автономной формулировки краевых задач для волн E_{0 m} и H_{0 m} .

Численные исследования подтверждают априорные высказывания относительно действительности собственных значений симметричных краевых задач. На рис. 2 приведена дисперсионная характеристика симметричной Е-волны, как совместное решение уравнений (29) и (25). На рис. 3 показана зависимость амплитуды поля от радиальной координаты. Как видно из рисунков, волна является быстрой (ее фазовая

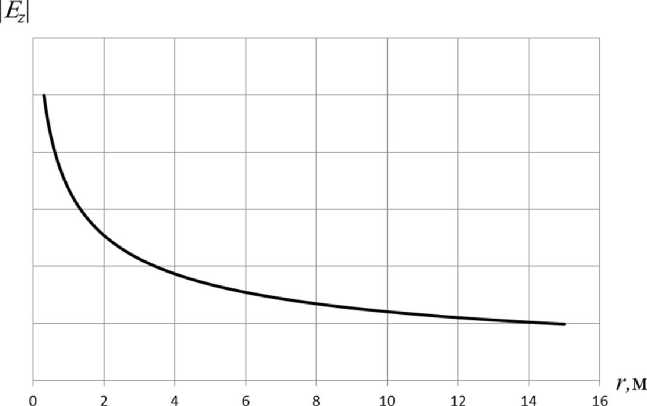
Рис. 3. Распределение модуля компоненты E_z от радиальной координаты для следующих параметров: а = 0,3 м;

N = 1 • 10 24 м ^{- 3}; о = 56 • 10⁶ См/м; k₀a = 1,95, в / к 0 = 0,95

Р1/^о

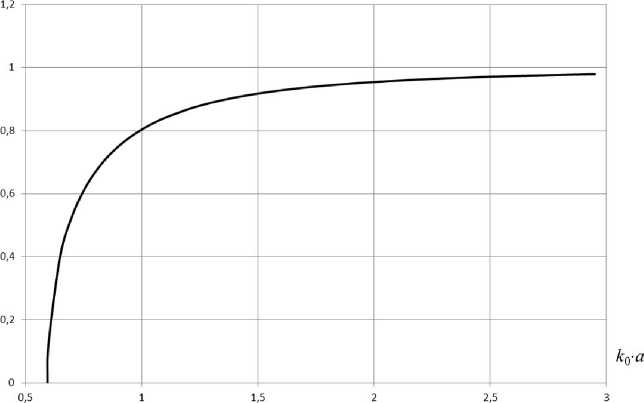
Рис. 4. Дисперсионная характеристика симметричной волны для следующих параметров структуры: а = 0, 3 м; о = 56 • 10⁶ См/м; N = 1 • 10 24 м ^{- 3}

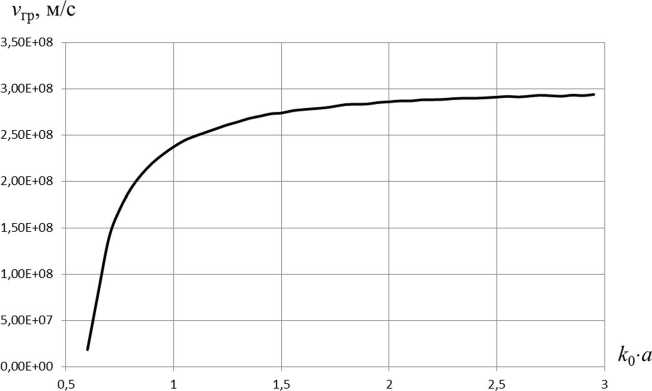
Рис. 5. Зависимость групповой скорости от частоты скорость vф > с, с — скорость света в вакууме) с экспоненциально убывающим при удалении от направляющей структуры полем. Такую волну в литературе принято [1] называть волной Ценне-ка. Вокруг нее длительное время (более 100 лет) идут научные споры, которые даже привели [11] к отрицанию ее существования. В указаной работе на основе того, что в двумерной плоской направляющей структуре групповая скорость волны оказалась (по проведенным исследовани-

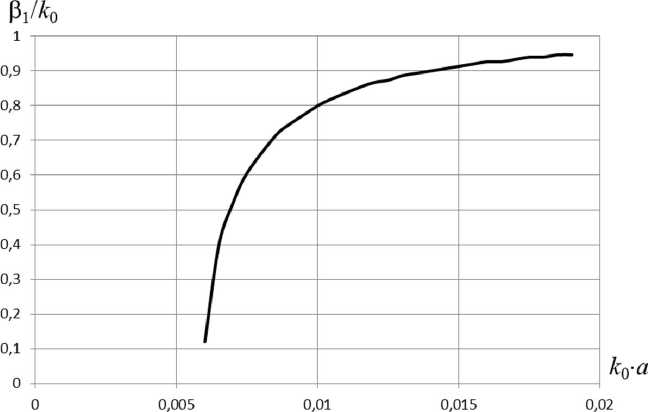
Рис. 6. Дисперсионная характеристика симметричной волны для следующих параметров структуры: а = 0, 3 м;

о = 56 • 10⁶ См/м; N = 1 • 10²⁰ м ^{- 3}

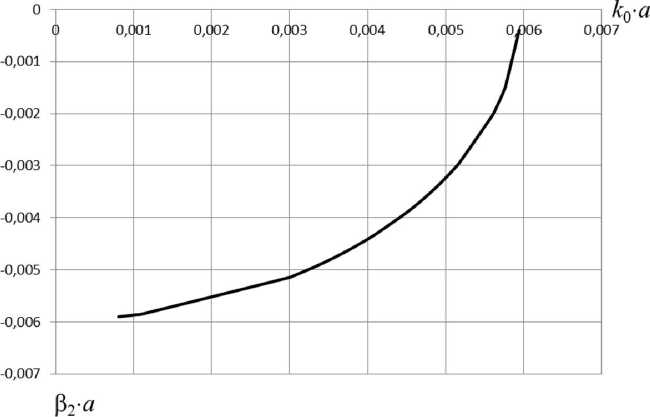
Рис. 7. Характеристика затухания симметричной волны для следующих параметров структуры: а = 0, 3 м; о = 56 • 10⁶ См/м; N = 1 • 10²⁰ м ^{- 3}

ям) больше скорости света в окружающей среде, волне Ценнека отказано в существовании: она была названа волной «призраком», то есть получила мистическую характеристику.

Поскольку, как видно из численных результатов, волна имеет либо чисто действительное (на частотах выше критической, рис. 2) продольное волновое число, либо чисто мнимое (на частотах ниже критической, рис. 2), групповая скорость ее была вычислена как v _гр = dю/d p , то есть прямым численным дифференцированием. На рис. 4, 5 приведены дисперсионная характеристика симметричной Е-волны (рис. 4) и соответствующая ей зависимость групповой скорости от частоты. Как видно из приведенных результатов, рассматриваемая симметричная Е-волна имеет v гр <  с , то есть вполне физична.

При уменьшении концентрации электронов плазмы критическая частота уменьшается. На рис. 6–9 приведены зависимости фазовых постоянных Р 1 и коэффициентов затухания Р ₂ в запредельной области при различных значениях концентрации электронов плазмы. Уменьшая

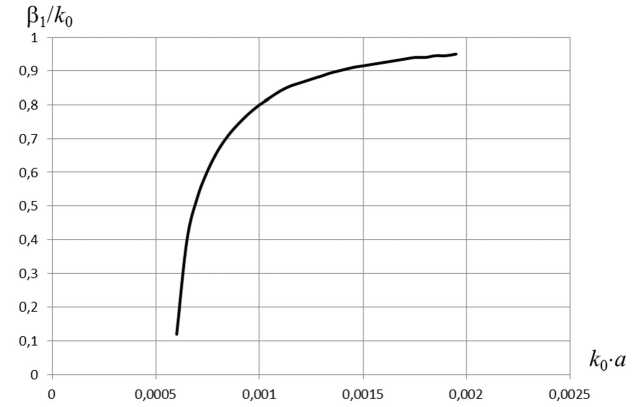
Рис. 8. Дисперсионная характеристика симметричной волны для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10 6 См/м; N = 1 ■ 10¹⁸ м ^{- 3}

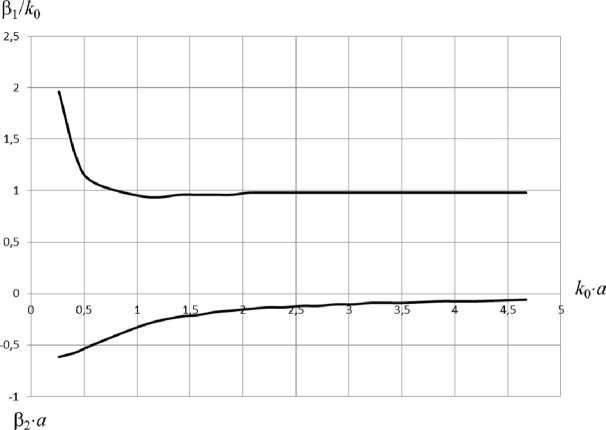
Рис. 10. Дисперсионная характеристика и характеристика затухания волны с индексом n = 1 для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10 6 См/м; N = 1 ■ 10 24 м ^{- 3}

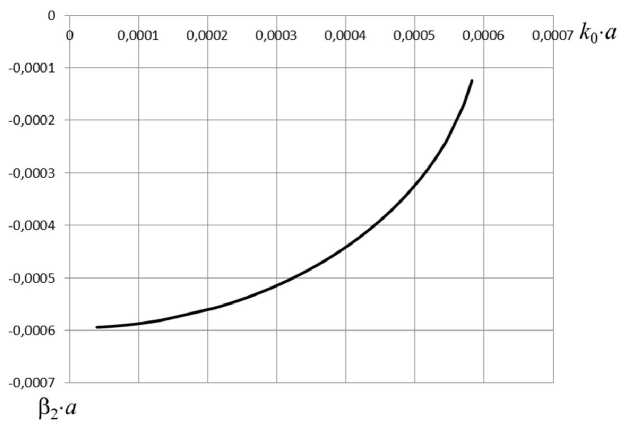
Рис. 9. Характеристика затухания симметричной волны для следующих параметров структуры: а = 0, 3 м; о = 56 ■ 10 6 См/м; N = 1 ■ 10¹⁸ м ^{- 3}

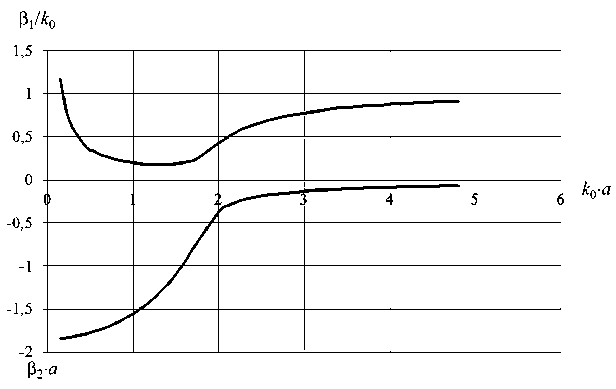
Рис. 11. Дисперсионная характеристика и характеристика затухания волны с индексом n = 1 для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10 6 См/м; N = 1 ■ 10 25 м ^{- 3}

концентрацию N электронов, в пределе переходим к направляющей структуре – проводящий цилиндр в пустоте. В этом случае критическая частота рассматриваемой волны стремится к нулю.

Таким образом, исследования показали, что проводящий цилиндр может направлять симметричную Е-волну. Волна является быстрой, поверхностной волной с экспоненциально убывающим по радиальной координате полем, таким образом, волна Ценнека, как решение двумерной краевой задачи для цилиндрической структуры, существует. Эта волна описывается решением квази-самосопряженной краевой задачей: для нее выполняется нулевое граничное условие на бесконечности.

Численные исследования показали, что найденное решение дисперсионного уравнения (25) является единственным, а уравнение (30) вообще не имеет решений. Таким образом, можно сделать вывод, что однопроводная линия передачи в виде цилиндрического проводника с конечной проводимостью может направлять единственную симметричную волну типа Е, которую в соответствии с существующими канонами следует называть волной Ценнека.

Несимметричные волны

Краевая задача для несимметричных волн ( n ^ 0) является несамосопряженной: для нее не выполняется второе условие самосопряженности [2–4] – граничные условия прямой и сопряженной краевых задач не могут быть эквивалентными. Поскольку собственные значения несамосопряженных краевых задач в общем случае являются комплексными величинами, волновые числа, как решения дисперсионного уравнения (24), в общем случае должны быть комплексными.

На рис. 10 изображены частотные зависимости действительной и мнимой частей продольного волнового числа волны с индексом n = 1. Как видно из приведенных характеристик, в широком диапазоне частот волна распростра-

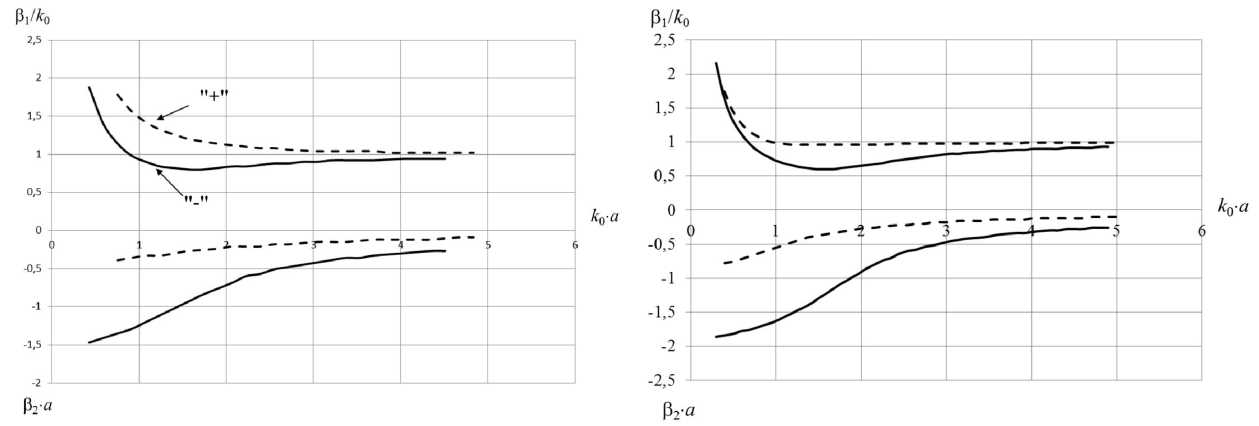
Рис. 12. Характеристики дисперсии и затухания волн Рис. 14. Характеристики дисперсии и затухания волн с индексом n = 2 для следующих параметров структуры: с индексом n = 2 для следующих параметров структуры: а = 0,3 м; ст = 56 • 10 6 См/м; N = 1 • 10 24 м ^{- 3} а = 0,3 м; ст = 56 • 10 6 См/м; N = 5 • 10 24 м ^{- 3}

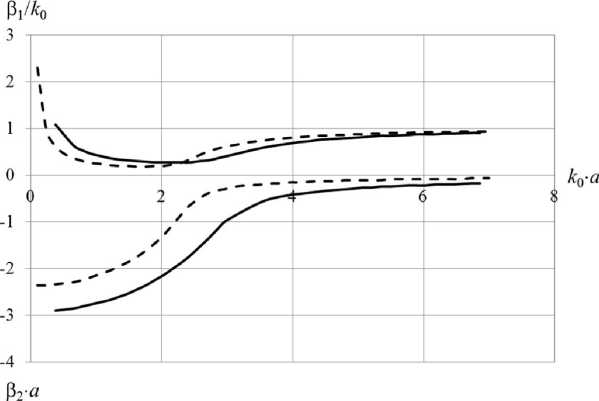
Рис. 13. Характеристики дисперсии и затухания волн с индексом n = 2 для следующих параметров структуры: а = 0,3 м; ст = 56 • 10 6 См/м; N = 1 • 10²⁵ м ^{- 3}

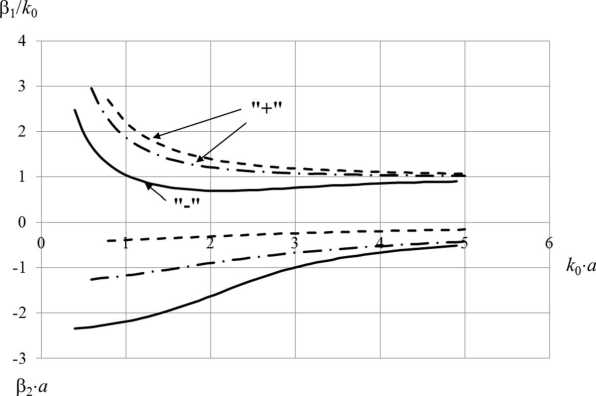
Рис. 15. Характеристики дисперсии и затухания волн с индексом n = 2 для следующих параметров структуры: а = 0,3 м; ст = 56 • 10 6 См/м; N = 5 • 10²⁵ м ^{- 3}

няется практически без дисперсии со скоростью, близкой к скорости света в окружающей среде. При этом сначала (на высоких частотах) волна является быстрой, затем при уменьшении частоты становится медленной. Приведенным на рис. 10 характеристикам соответствуют значения поперечных волновых чисел а = у + i 5 , у которых 5 >  0. Таким образом, мы имеем волну с нарастающим по радиальной координате полем: в области, где в / к о <  1, это вытекающая волна, в области, где в / к о >  1, это волна медленная несобственная. При меньшей концентрации электронов плазмы, рис. 11, частотное разделение волн по характеру дисперсии более явно выраженное: на высоких частотах волна быстрая с сильной дисперсией, на низких – медленная.

Численные исследования показали, что при индексе n = 1 решения дисперсионного уравнения, приведенные на рис. 10, 11, являются единственными. На рис. 12 показаны решения дисперсионного уравнения (24), полученные при n = 2. Как видим, при n = 2 число волн удвои- лось. При изменении концентрации электронов в плазме, рис. 13, 14, характер частотных зависимостей продольного волнового числа претерпевает значительные изменения, но при всех значениях N волны остаются несобственными, то есть имеют нарастающее по радиальной координате поле. При этом они могут быть как быстрыми (Р1 / ко < 1) вытекающими волнами, так и медленными несобственными (в / ко > 1). Во всех случаях распространение волн сопровождается, рис. 15, их большим затуханием в продольном направлении.

При n = 3 имеем уже три волны, рис. 16: две волны медленные – штриховые и штрихпун-ктирные линии, одна быстрая – сплошные линии. Таким образом, выявили интересную принципиальную закономерность: индекс n определяет число несобственных волн, существующих в рассматриваемой направляющей структуре. Их комплексность объясняется радиационными потерями – излучением поля в окружающую среду. Поля таких волн локализируются вблизи

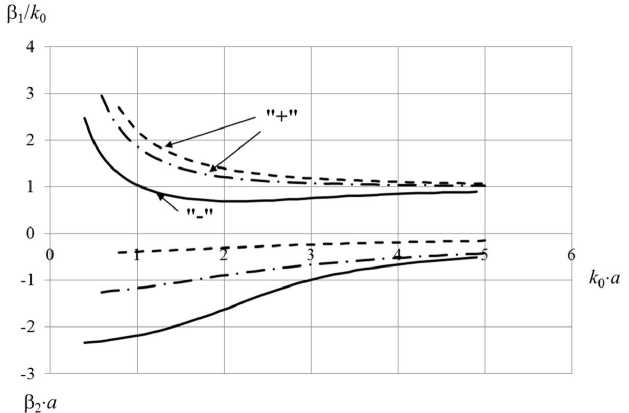
Рис. 16. Характеристики дисперсии и затухания волн с индексом n = 3 для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10 6 См/м; N = 5 ■ 10 22 м ^{- 3}

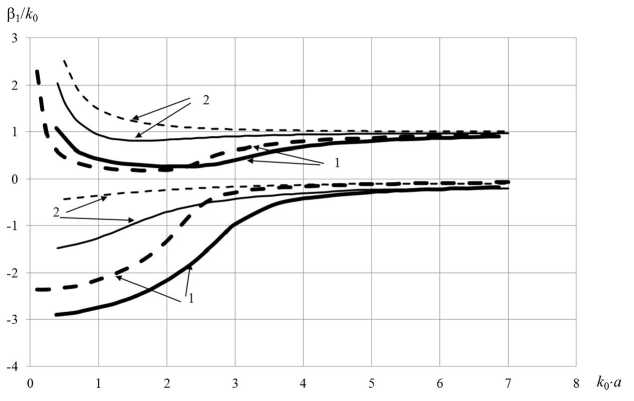
Рис. 17. Характеристики дисперсии и затухания волн с индексом n = 2 для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10 6 См/м; при разных концентрациях электронов: 1 — N = 2 ■ 10²⁵ м ^{- 3} (толстые линии); 2 — N = 1 ■ 10 24 м ^{- 3} (тонкие линии)

источника, имеют значимость только в ближней зоне и в переносе энергии вдоль направляющей структуры не участвуют.

На рис. 17, 18 показана трансформация дисперсионных зависимостей при изменении концентрации N электронов. Как видно из приведенных результатов, свойства несобственных волн в значительной мере управляются параметрами окружающей направляющую структуру плазмой.

Общие свойства всех несимметричных волн: все они несобственные – не удовлетворяют условию излучения, могут быть как быстрыми, так и медленными. Характерной особенностью волн рассматриваемой направляющей структуры является ограниченность модового спектра. Последний формируется только азимутальным индексом n .

На рис. 12, 16 указано соответствие дисперсионных характеристик уравнениям (26) с различными знаками ( ± ) перед радикалом.

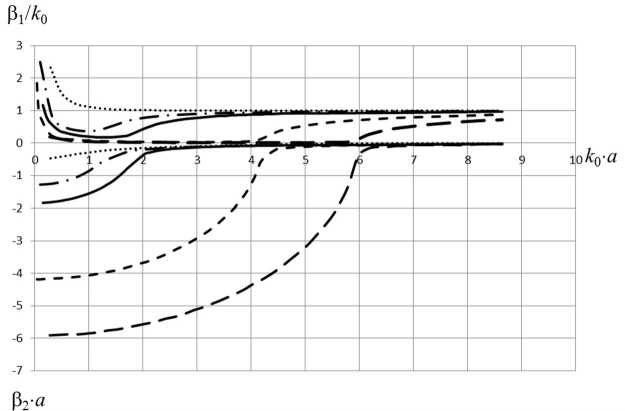
Рис. 18. Характеристики дисперсии и затухания волн с индексом n =2 для следующих параметров структуры: а = 0,3 м; о = 56 ■ 10⁶ См/м; при разных концентрациях электронов: N = 2 ■ 10²³ м ^{- 3} (точечная линия); N = 0,5 ■ 10²⁵ м ^{- 3} (штрих-пунктирная); N = 1 ■ 10²⁵ м ^{- 3} (сплошная линия); N = 5 х х 10²⁵ м ^{- 3} (пунктирная линия); N = 1 ■ 10²⁶ м ^{- 3} (штриховая линия)

Заключение

Решена внешняя краевая задача о распространении электромагнитного поля вдоль проводящего цилиндра в слое изотропной плазмы. Обоснованно разделение волн направляющей структуры на HE _nm и EH _nm . На основе составленного дисперсионного уравнения проведено исследование характеристик волн проводящего цилиндра, помещенного в неограниченную плазменную среду. Показано существование в такой структуре собственных и несобственных волн. Численные исследования показали, что собственной волной является быстрая поверхностная волна E₀₁. Ее в данном случае можно отождествлять с волной Ценнека. Несимметричные волны HE _nm и EH _nm являются несобственными волнами: либо вытекающими, либо медленными несобственными. Направляющая структура в виде цилиндрического проводника может работать как протяженная линия передачи только на волне типа Ценнека – волна E₀₁. На остальных волнах структура является сильно излучающей.