Computational experiment for a class of mathematical models of magnetohydrodynamics

Consider the first initial-boundary value problem for the system modeling the motion of the incompressible viscoelastic Kelvin - Voigt fluid in the magnetic field of the Earth

(1 — xA ) v t = vAv — ( v • V ) v

Vv = 0 , Vb = 0 ,

— ¹ Vp — 2О x v + —( V x b ) x b + f ¹ , ρ             ρµ

b_t = 5 Ab + V x ( v x b ) + f ² ,

v ( x, 0) = v 0( x ) , b ( x, 0) = b ₀( x ) , x E D,                         (2)

v ( x, t ) = 0 , b ( x,t ) = 0 , ( x,t ) E dD x R ₊ .                      (3)

Here vector-functions v and b correspond to velocity and magnetic induction respectively, p is the pressure, vector-functions f ¹ and f ² correspond to external influences on the fluid 1

and magnetic field respectively; О = ^ V x v is angular velocity, V is operator of Hamilton, 5 is the magnetic viscosity, у is the magnetic permeability, p is the density. D C Rⁿ is the cylinder’s domain with the boundary dD of the class C A

This work continues investigations of magnetohydrodynamics models which were started by the authors in [2,3]. Its distinctive feature is that there are vector-functions f k = ( f i k . f 2 ...., f n ) iⁿ the right part of equations (1).

The first initial-boundary value problem (1) - (3) is reduced to an abstract Cauchy problem for a semi-linear non-autonomous Sobolev type equation. On the base of the solvability theory of the indicated problem the theorem of existence and uniqueness of the solution of the stated problem is proved. The solution itself is a quasi-stationary semitrajectory. The description of the problem’s extended phase space is obtained. The results of the computational experiment are represented. The results of part 1 are taken from [4], the results of part 2 are obtained on the base of the results [2]. During the computational experiment the methods of solution of the initial-boundary problem (1) - (3) are used. They were described in [3]. Also we used the software package [5].

1.    Semi-Linear Non-Autonomous Sobolev Type Equations

Consider the Cauchy problem for the semi-linear non-stationary Sobolev-type equation u (0) = u 0, Lui = Mu + F (u) + f (t).

Here the operator L E L ( U ; F ) , i.e. it is linear a nd continuous, ker L = { 0 } ; the operator M : dom M ^ F is linear and closed and it is densely defined in U, i.e. M E Cl ( U ; F ); U and F are Banach spaces. Let U M be the lineal dom M equipped with the norm of the graph || | • ||| = || M • Ц^ - + || • ||_M. We assume that F E C~ ( UM ; F ) , and the function f E C ~ (R +; F ) .

Consider (4) under condition that the operator M is strongly ( L,p )-sectorial [4]. It is well known that in this case a solution of this problem exists not for all u 0 E U M , and even if it exists it may be non-unique. So we introduce two definitions: the extended phase space and quasi-stationary semi-trajectory.

It is well known that if the operator M is strongly ( L,p )-sectorial, then U = U ⁰ • U ¹ , F = F ⁰ ^F ¹ , where

U0 = {ф EU : U tф = 0 3t E R+},  F0 = {0 EF : Ft 0 = 0 3t E R+} are the kernels, and

U ¹ = {u EU : lim U t u = u}, t → 0+

F ¹ = {f EF : t l i m F t f = f}

are

Ft

the images of the analytic solving semigroups U t

= 2 П- у L L ( M ) е-Мц (Г C S La ( M )

A [ RL ( M ) d 2 ni

Γ

is a contour such that arg ц ^ ± 0 when

Γ

|ц| ^ + to) of the linear hornogeneous equation Li = Mu. Let L k ( M k ) Ire a restriction of the operator L ( M ) оn U^k ( U^k П dom M ) , k = 0 , 1 . Then L k : U^k ^ F^k, M k : U^k П dom M ^ F^k, k = 0 , 1; and restrictions M 0 arid L ₁ of the оperators M

and L on the spaces U ⁰ П dom M and U ¹ respectively are linear continuous operators and

they have bounded inverse operators.

So we reduce (4) to

Rui0 = n 0 + G (n) + g (t), n 0 (0) = n о, u1 = Su1 + H (u) + h (t), u1 (o) = u 0, where uk E Uk, k = 0,1, u = u0 + u1, operators R = M0 1Lо, S = L01M0, G = M-1 (I — Q) F, H = L -1QF, g = M3" 1( I— Q) f, h = L -1 Qf. Here Q EL (F)(= L (F; F)) is the corresponding projector.

We study such quasi-stationary semi-trajectories of (4), for which Rui ⁰ = 0 . Assume that the operator R is bisplitting . i.e. its kernel ker R and image im R are complemented In the space U. Deirote U ⁰⁰ = ker R, arid U ⁰¹ = U ⁰ OU ⁰⁰ is a complement of the subspace U ⁰⁰ . Then the Erst equation of (5) Is reduced to the form Ru t⁰¹ = u ⁰⁰ + u ⁰¹ + G ( u ) + g ( t ) , where u = u ⁰⁰ + u ⁰¹ + u ¹ .

Theorem 1. Let the operator M be strongly ( L,p)-sectorial, and the operator R be bisplitting. Let there exist a quasi-stationary semi-trajectory u = u ( t ) of equation (4). Then it satisfies the following relations

0 = u ⁰⁰ + u ⁰¹ + G ( u ) + g ( t ) ,   u ⁰¹ = const .

It is known that if the operator M is strongly ( L,p )-sectorial then the operator S is sectorial. So it generates an analytic semigroup on U 1. Denote it as {Ut : t >  0 } because the operator Ut In fact Is a restrict Ion of the operator Ut о n U ¹ . The fa, ct that U = U ⁰ • U ¹ shows that there exists a projector P E L ( U ) corresponding to this splitting. It can be shown that P E L ( UM ) . Then tlre space UM splits Into the direct sum UM = UM ■ U_M so that the embedding UM C U^k, k = 0 , 1 Is dense and continuous. Symbol Av denotes the Frechet derivative at v eV of the о perator A, defined on som.e Banach space V.

Theorem 2. Let the operator M be strongly ( L,p)-sectorial, the operator R be the bisplitting one, the operator F E C^ ( UM ; F ) , the vector-function f E C^ю (R₊; F ) . Let the following conditions be satisfied:

• (i)    0 = u 01 + ( I — PR )( G ( u ⁰⁰ + u 01 + u 1) + g ( t )) in the neighborhood Ou ₀ C UM of the point u ₀:

• (ii)    the projector PR E L ( UMM ) , and the operator I + PRG'_{u 0} : UM ^ UMM is the topological linear isomorphism ( U °° = UM AU ⁰⁰);

τ

• ⁽ⁱⁱⁱ⁾    / IIUt^n (U1; U1) ^dt< ^^^{T E R}+' 0               ^M

2.    The Existence of the Unique Solution

Then there exists a unique solution of (4), which is a quasi-stationary semi-trajectory of equation (4).

Now let Uk arid F_k Ire Banach sprices, operators A_k E L ( Uk, F_k ) , arid operators B_k : dom Bk ^ F be linear and closed with domains dom Bk dense In Uk, k = 1 , 2 . Construct spaces U = U 1 x U ₂ , F = F i x F 2 and operators L = A 1 ® A ₂ , M = B 1 ® B ₂ . By construction operator L E L ( U ; F ) , and operator M : dom M ^ F is linear, closed and densely defined. In U dom M = dom B 1 x dom B ₂ .

Theorem 3. Let the operators Bk be str ongly ( Ak ,p_k )-secto rial, k = 1 , 2; a nd p 1 > p ₂ . Then the. operator M is sti"ongly ( L,p^-sectorial.

Following [2] consider problem (2), (3) for system (1) transformed to the form

(1 — xA ) vt = v Av — ( v • V ) v —

- Vp — 2Q x v + —( V x b ) x b + f ρ             ρµ

V ( V- v )=0 , V ( V- b )=0 , bt = 6 Ab + Vx ( v x b ) + f ² .

Then similarly to [2] we introduce the spaces U and F the operators L and M generated by the problem (2). (3) for the transformed system (1). Strong ( L, 1)-sectorialness of the operator M under the assumption \ ¹ / ° ( A ) , A = V ² En EF is identity n x n matrix) is established using the Theorem 3. The form of the nonlinear operator F is similar to the one in [2], only the first and the second elements of the vectorcolumn include the term f 1, and the last element includes f 2. Belonging of F to the class C^ю ( U m ; F ) is proved by calculation of the Frechet derivatives of this operator. Therefore, all assumptions of Theorem 1 and Theorem 2 are satisfied. Consequently, the following result holds.

Theorem 4. 7/ к - ¹ / ° ( A ) U о (_ L) , ^ten for all u 0 G M and some T E R₊ there exists a unique solution u = ( u_CT, 0 , u_p,u_b ) of (1) - (3) which is a quasi-stationary trajectory. Moreover, u ( t ) G M .for all t G (0 , T ).

Here A_CT is a restriction of the operator A on the corresponding subspace of solenoidal vectors. u_CT, 0 , u_p,u_b are the elements of the correspoiiding subspaces of Banach space U [2]: M is the extended phase space of (1), (3), which has the following form

M = {u G UM : u_n = 0 ,b_n = 0 , up = П( vA_CT — ( u_CT • V ) u_CT— 2fi x u_CT + ( V x b_a ) x b_a + f 1) }.

3.    Computational Experiment

Introduce a cylindrical coordinate system ( r, ф, z ) with center O on one side of the surface of the cylinder D and combine Oz axis with the cylinder axis. In the future, we will assume that a flow of fluid is axially symmetric.

Figures 1-3 show the charts of surfaces of fluid flow velocity components at time t * = 2 s. obtained for the following values of the problem parameters: x = 2 , 7 ni s². v = 0 , 00328 iii² / s. ц = 1 p = 1000 kg m³. 6 = 0 , 1. r 0 = 0 , 1 nn z 0 = 0 , 2 m. Vector-functions’ components f 1, f ² had the form fr = 0 , 001 r ( r 0 — r ) sin( nt ) кg • m/s², f^ = fZ = 0, fr ² = 0 , 001 r cos( nt ) T, fф 2 = fZ 2 = 0. Vector functions v ₀( r, z ) and b ₀( r, z ) in the initial conditions (2) are given in the form v 0 = ш 0 ri_r, b 0 = b_r 0 i_r , where ш 0 = 0 , 25 1 / s, b_r 0 = 0 , 00005 T. The initial conditio ns for vector-functions F- A are given in the form: F ( r, z, 0) = 0 , 25 ш 0 r (2 zi_r — riz ), A ( r, z, 0) = —b_r 0 zi_v. The boundary and initial conditions for vector-functions ^ and A are given in the form: ^ ( r, z,t ) = 0 , A ( r, z,t ) = 0 , ( x, r, t ) G dD x R₊.

Conducted computational experiments show a computational stability and computational efficiency of the developed algorithm for numerical solution of initialboundary problem (1) - (3).

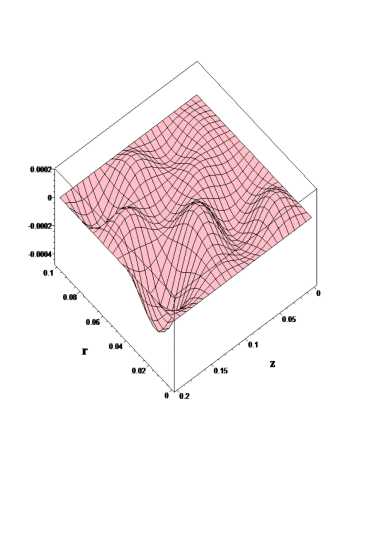
Fig. 1. Chart of surface radial component of fluid flow velocity V r = V r ( Г, Z,t * )

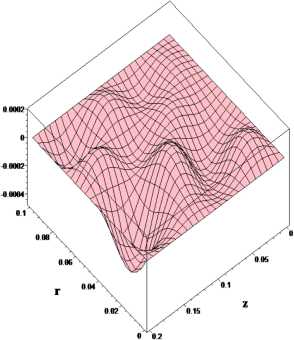
Fig. 2. Chart of surface transversal component of fluid flow velocity

V ф = V ф ( r,z,t * )

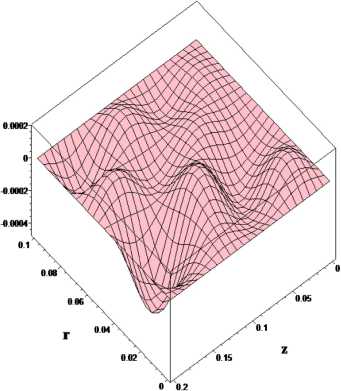
Fig. 3. Chart of surface axial component of fluid flow velocity v z = v z ( r, z, t * )