Conditions for electric breakdown in the lower ionosphere due to a lightning discharge

Conditions are theoretically studied, under which a breakdown is realized in the lower ionosphere above a thunderstorm after a positive cloud-to-ground (+CG) lightning discharge. Two altitudes are seen as candidates for a breakdown initiation: ( i ) at which the relaxation time equals the discharge time, and ( ii ) at the "knee" of the conductivity profile. According to this, a criterion of a breakdown occurrence is formulated. The conductivity is the key factor for a breakdown onset (i.e. more important than the charge moment change), due to its large variability at these heights.

Lightning discharges produce strong quasielectrostatic fields (QSF) and electromagnetic pulses, which can provoke red sprites and haloes in the lower ionosphere [1], electron density variations in the middle ionosphere [2], etc. According to a hypothetical mechanism, sprites are realized through a conventional breakdown in the lower ionosphere above a lightning discharge due to the QSF. A breakdown is realized when the applied electric field | E | exceeds the breakdown threshold electric field E k = 3.2 × 10⁶ N/N 0 [V/m], where N is the neutral density at altitude z , and N ₀ is the density at the sea level z= 0 [3]. We examine the conditions, under which the time peak of the QSF exceeds the breakdown electric field E k , by a 2D analytical quasistatic model [4] (the quasi-static conditions are relevant for horizontal scale typical for sprites [5]). Among simplifying assumptions used [4] we accept that the thundercloud charge involved in lightning is distributed at altitude Z Q with surface density ρ ( t ) at time t . We obtain the spatial and temporal distributions of the electric field E and of its potential U as solutions of the continuity equation ∇⋅ j = 0 for the Maxwell’s current density j (above a thunderstorm j = j C + j D , where j C and j D are the conduction and displacement currents densities). The model region is bounded by altitudes z= 0 (the sea level) and Z_E= 100 km. The boundary conditions are: ( a ) U= 0 at z= 0 and Z E ; ( b ) the vertical electric field has a jump of amount ρ/ε ₀ at height Z Q ( ε ₀ is the dielectric constant). We accept as the initial condition at the lightning beginning at time t= 0 that E is the DC electric field generated by the thundercloud charge at t= 0.

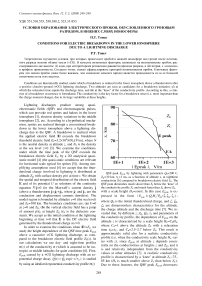
In order to examine the conditions when | E |>E k , we study the height dependence of the QSF time peak E peak above a causative +CG lightning discharge, as compared to the breakdown electric field profile E k ( z ). In our calculations we use day- and night-time profiles σ ( z ) of the conductivity σ (which is assumed to be isotropic) at middle latitudes for quiet conditions [6]. First, E _peak caused by a +CG lightning discharge with an exponential charge decay Q ( t ) = Q ₀ exp( - t / τ _L ) is studied by using an idealized exponential conductivity profile σ ( z )

QSF peak E _peak by lightning with parameters Q ₀=200 С , Z_Q= 10 km, τ _L=1 ms, as a function of altitude z, at nighttime conductivity [6] compared to breakdown electric field Е _k . The QSF peak diminishes much slower than Е _k below the ‘knee’ of the conductivity profile Z _C and much faster than Е _k above Z _E. with a scale height H _σ =const. In this case E _peak is expressed in the form | E _peak | = Q ₀ H _σ ^{- 2} P_QS ( ζ , ζ _Q , ζ _L ) , where Q ₀ is the initial thundercloud charge, and ζ , ζ _Θ , ζ _L are dimensionless characteristics for the altitude, the charge altitude and the discharge time [7]. We revealed that, by different z , Z Q , Q 0 , τ L and parameters of the conductivity profile, the dependence of E peak on the altitude z is characterized by a scale height H E ≈ C σ H σ , where C σ ≈ 1 above the altitude Z E with a relaxation time τ R = τ L , and C σ ≈ 2.5–2.7 below Z E . This result is approximately valid also for a realistic conductivity profile (i.e. when the conductivity scale height H σ varies with z ), since E peak at altitude z depends essentially on the conductivities at heights z and Z Q , and it is and relatively independent from the conductivity values at other altitudes [7]. A realistic conductivity profile is characterized by a ‘knee’ at altitude Z_C ~75– 85 km ( H _σ is much smaller above Z_C than below Z_C ). Due to these features, the QSF peak E _peak decreases:

Условия образования электрического пробоя , обусловленного грозовым разрядом , в нижних слоях ионосферы

• ( i )    much slower than E_k below both altitudes Z_E and Z_C ; and ( ii ) much faster than E_k above Z_E and Z_C . This conclusion is demonstrated by our computational results for nighttime conductivity in figure. Thus, we conclude that a breakdown, if realized, is initiated in the lower ionosphere, either close to the altitude Z E , or close to Z C . Therefore, a breakdown occurs if at least one of the following conditions is fulfilled:

Q0 > Ha Ek /PQS (Z = ZE / Ha , Z Q , Z L ) ’ or Q0 > Ha Ek / PQS (Z = ZC / Ha , Z Q , Z L ) '

These results show that the conductivity profile, being a highly variable characteristic in the lower ionosphere [6, 8], is more important factor for the occurrence of a breakdown than the charge moment change of the causative lightning. This can probably explain realization of sprites due to rather feeble lightning discharges and their occurrence usually at night.