Conditions for the Limit Summability of Solutions of Nonlinear Elliptic Equations with Degenerate Coercivity and L1-Data

At present there is an extensive literature devoted to the study of the Dirichlet problem for second-order nonlinear elliptic equations in divergence form with L ¹ -data or measures as data. Within the investigations on the subject, the notions of weak, entropy, and renormalized solution of the considered problem were introduced and theorems on the existence, uniqueness, and summability of such solutions were proved. In this connection, see, e.g., [1–13], where equations with leading coefficients satisfying the usual coercivity condition were considered.

• ^# Работа выполнена при финансовой поддержке Министерства наукии высшего образования Российской Федерации в рамках реализации программы регионального Азово-Черноморского математического центра по соглашению № 075-02-2025-1620.

• (0 2025 Kovalevsky, A. A.

At the same time, there are many works (see, e.g., [14–25]) concerned with the study of different types of solutions to the Dirichlet problem for equations of the form

n

— ^ D i a i ( x, u, Vu) + a o (x, u, Vu) = f                    (1.1)

i =1

in a bounded open set Q in R ⁿ , n ^ 2, where f G L m (Q), m ^ 1, and the set of functions a i : Q x R x R n ^ R, i = 1 ,..., n , satisfy a degenerate coercivity condition like

£ а^ЯЬ >  (TTH) T                 (1.2)

for a.e. x G Q and every s G R and £ G R n . Here, the parameters p G (1 , n ), т >  0, and c> 0 are prescribed, and if we formally set т = 0, inequality (1.2) becomes the usual coercivity condition. As for the function a 0 in (1.1), it can be zero or satisfies certain conditions.

We also note that there are a number of works concerned with the study of solutions of equations of the form (1.1) with f G L ^m (Q), m ^ 1, in different cases of a more general degenerate coercivity condition as compared to condition (1.2). In this relation, see, e.g., the papers [26–33]. However, these works do not contain results on the limit summability of solutions similar to ours.

The further content of this paper is organized as follows. In Section 2, we give initial assumptions, necessary definitions, and basic facts used in the sequel.

In Section 3, we state the definition of entropy solution of the Dirichlet problem under study and recall the corresponding existence result and the summability properties of an entropy solution established in [17]. In particular, Proposition 3.1 says that if u is an entropy solution of the considered problem, then, for every A G (0 ,r ), we have | 5u| G L ^A (Q). Here, 6u is the gradient of the solution u and r = n(p — 1 — т)/(n — 1 — т ). We note that this result coincides with a result obtained in [15] in the case where the leading coefficients of equation (1.1) have only a limited growth rate with respect to the unknown function itself and the lower order term is zero. We also note that Propositions 3.1 together with a result given in Section 2 implies that if r >  1 and u is an entropy solution of the considered problem, then, for every A G [1 ,r ), we have u G W o1 ^,A (Q). In the same section, we also give a useful integral identity for an entropy solution (see Proposition 3.2). A similar result was obtained in [34] in the case of another class of elliptic equations with L ¹ -data.

In Section 4, for an entropy solution u of the considered problem, we give estimates of the measures of the sets {| u | ^ k} and {| 5u | ^ k} with k ^ 1 (see Propositions 4.1 and 4.2). These estimates involve the function f : [0 , + ot ) ^ R defined by the right-hand side f of equation (1.1) as follows: for every s G [0 , + to ) , f ( s ) is the integral of the function | f | over the set {| f | ^ s } . In the case of equations with usual coercivity condition, similar estimates were established in [10].

In Section 5, using results of the previous section, we prove our main theorems on the limit summability of entropy solutions of the considered problem (see Theorems 5.1 and 5.2). The statement of each of these theorems includes an integral condition involving the function f . In particular, by the integral condition of Theorem 5.2, if u is an entropy solution, then | 5u | G L r (Q). The obtained theorems generalize the main results of the paper [10]. In the same section, we give some corollaries of Theorem 5.2 which provide conditions for the belonging of entropy solutions to TWq ^,r (Q) and, in particular, to W q ^{1 , 1} (Q) .

In Section 6, we study weak solutions of the considered problem. Here, we already assume that the leading coefficients of equation (1.1) have a limited growth rate with respect to the unknown function itself. The main result of the section is Theorem 6.1 which asserts the existence of a weak solution of the considered problem belonging to W 1^,r (Q) under the integral condition of Theorem 5.2 and an additional requirement on τ . Some corollaties of Theorem 6.1 are also given. In particular, according to Corollary 6.3, if 2 — 1 /n C p C 2, т (n — 1) = n(p — 2) + 1, A >  (n — p ) / ( n — 1), and f [ln(1 + | f | )] ( ^n-p ) / ( ^{n- 1}) [lnln( e + | f | )] ^a G L ¹ (Q), then the considered problem has a weak solution. This result is stronger than Theorem 1.2 in [20] given for the case p = 2. Moreover, in the case 2 — 1 /n C p C 2, Corollary 6.3 is a stronger result than Theorem 6 in [24], where it is required, as in [20, Theorem 1.2], that f ln(1 + | f | ) G P(Q).

Finally, in Section 7, we give two examples. The first one is an example of the functions a i satisfying the growth, degenerate coercivity, and strict monotonicity conditions stated in Section 3. In the second example, we consider a function f G L ¹ (Q) which does not belong to L ^{1+ e} (Q) for any e >  0 and satisfies the conditions in the statements of the results in Sections 5 and 6.

2.    Preliminaries

Let n G N, n ^ 2, let Q be a nonempty bounded open set in R ⁿ , and let p G (1 , n ).

We define p * = np/(n — p ). Recall that W₍ ^{1 ,p} (Q) C L^p* (Q) and there exists a positive constant c _n ,p depending only on n and p such that, for every function v G W₍ ^{1 ,p} (Q),

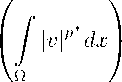
1 /p *

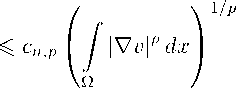
(2.1)

In this connection, see, e.g., [35, Chapter 7].

For every k >  0, let T k : R ^ R be the function such that

T k ( s ) = |

s           if |s| C k, k sign s if |s| > k.

As is known, if A >  1, v G W q^1,A (Q) , and k >  0, then T k ( v ) G W q^1,A (Q) and, for every i G { 1 ,... , n } ,

(2.2)

D i T k (v) = D i v • 1 {| v | } a.e. in Q .

We denote by T 01 ^,p (Q) the set of all functions v :Q ^ R such that, for every k >  0, T k (v) G W q^1,p (Q) . Obviously, W ₀1 ^,p (Q) C T 01 ^,p (Q). However, the converse inclusion does not hold, which is easily verified. For every v : Q ^ R and every x G Q, we define k ( v,x ) = min { j G N : | v ( x ) | C j } .

Definition 2.1. Let v G T 01 ^,p (Q), and let i G { 1 ,... ,n}. Then b i v : Q ^ R is the function such that, for every x G Q, ^v( x ) = D i T k ( v,x ) (v)(x).

Definition 2.2. If v G T 01 ^,p (Q), then bv : Q ^ R ⁿ is the mapping such that, for every x G Q and every i G { 1 ,..., n } , ( bv ( x )) i = b i v ( x ).

Proposition 2.1. Let v G T 01 ^,p (Q) , and let i G { 1 ,..., n}. Then, for every k > 0, we have D i T k ( v ) = b i v • 1 {| v | } a-e- in Q -

This proposition and (2.2) imply that if v G W 01 ^,p (Q), then, for every i G { 1 ,...,n } , b i v = D i v a.e. in Q.

Proposition 2.2. Let v G T 01 ^,p (Q) , and let w G W 1^,p (Q) П L “ (Q) . Then the following assertions hold :

• (a)    v — w G T 01 ^,p (Q);

• (b)    for every k >  0 and every i G { 1 ,... ,n}, we have D i T k (v — w) = b i v — b i w a.e. in {| v - w | < k } .

Proposition 2.3. Let v G T 01 ^,p (Q) , let A G [1 ,p ] , and let | bv | G L ^X (Q). Then v G Wq^,A (Q) and, for every i G { 1 , . . . , n } , we have D i v = b i v a.e. in Q .

For every v G T 01 ^,p (Q) and every k >  0, we define

I k ( v ) = I |V T k ( v ) | ^p dx.

Ω

Proposition 2.4. Let v G T01,p(Q), and let k > 0- Then meas{|v| > k} C cn,pk~p* [Ik(v)]p*/p.

Proposition 2.5. Let v G T01,p(Q), and let k, l > 0- Then meas{|bv| > k} C Cn,pl-p [Il(v)]p /p + k~pIi(v).

As far as the proofs of Propositions 2.1–2.5 are concerned, we refer the reader, for instance, to Sections 1.1 and 1.5 in [36].

Finally, concluding this section, we state a useful result on the summability of a function with a prescribed behaviour of its distribution function.

Proposition 2.6. Let v : Q ^ R be a measurable function- Let а > 0,let ^ : [1 , + w ) ^ R be a nonnegative nonincreasing measurable function, and let k 0 ^ 1 - Assume that

+ ^

J ^ _da< + „ .

( V k ^ k 0 ) meas {| v | ^ k } C k ^-a ^ ( k ) .

Then v G L ^a (Q) -

For the proof of this result, see [10, Lemma 2.1].

3. Dirichlet Problem and Its Entropy Solutions

For every i G { 1 ,..., n } , let a i : Q x R x R n ^ R be a Caratheodory function. We assume that, for every k >  0, there exist a positive number C k and a nonnegative function g k G L 1 (Q) such that, for almost every x G Q, every s G R, | s | C k , and every £ G R n ,

n

£ |a i ( x,s,£ ) | ^{p/ ( p- 1)} C C k | £ | ^p + g k ( x ) .

i =1

(3.1)

In addition, we assume that there exist т G [0 ,p — 1) and c >  0 such that, for almost every x G Q, every s G R, and every £ G R n ,

Д                 c l £ l ^p

^T a i ⁽x,s,^{£ ) £} i >  (1 + | s | ) T .

(3.2)

Finally, we assume that, for almost every x G Q, every s G R, and every £,£ ‘ G R n , £ = £ ‘ ,

n

£ [a i ⁽x, s,^{£) —} a i ⁽x, s, ^{£ )}] ^{( £} i ^{— £} i ) >  ⁰ - i =1

(3.3)

Remark 3.1. If v G T 0^{1 ,p} (Q), w G W q^,p (Q) A L “ (Q), k >  0, and i G { 1 ,... ,n } , then a i (x, v, 8v)D i T k (v — w) G L 1 (Q). This is a consequence of (3.1) and Propositions 2.1 and 2.2.

Now, let f G L 1 (Q). We consider the following Dirichlet problem:

n

— ^^D i a i (x,u, V u ) = f in Q , u = 0 on d Q .                  (3.4)

i =1

Definition 3.1. An entropy solution of problem (3.4) is a function u G Tq^,p(Q) such that, for every v G C “ (Q) and every k >  0,

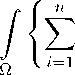
a i ( x, u, 6u)D i T k (u

—

v )

j dx C J

fT k (u — v ) dx.

The existence of an entropy solution of problem (3.4) follows from Theorem 2 in [17]. We note that along with inequalities (3.1) and (3.2), inequality (3.3) is also important for the proof of this theorem.

We define

n(p — 1 — т )         n(p — 1 — т )

q =-------------- , r =------;------- •

• n — p          n — 1 — т

Proposition 3.1. Let u be an entropy solution of problem (3.4) . Then the following assertions hold:

• (a)    for every A G (0 , q ) , we have u G L ^A (Q) ;

• (b)    for every A G (0 ,r ) , we have | ^u| G L ^A (Q) .

This result was established in [17] (see also [18, Proposition 3.2] for a more general case).

Remark 3.2. The summability properties described in Proposition 3.1 are the same as those of entropy solutions of the Dirichlet problem for the equations considered in [15]. In the case т = 0, these properties coincide with the known ones for equations with usual coercivity condition (see, e.g., [4]).

Remark 3.3. From Propositions 3.1 and 2.3, it follows that if r >  1 and u is an entropy solution of problem (3.4), then, for every A G [1 , r ), we have u G Wo ^,A (^).

Further, we give an additional information on entropy solutions of problem (3.4). For this goal, for every function v G T^ p fQj, we define

M ( v ) = { w G W q^1,p (Q) П L “ (Q) : a i (x, v, 8v)D i w G L ¹ (Q) , i = 1 ,..., n } .

By Proposition 2.2 and Remark 3.1, we have v G T01,p(n),  w G W01,p(Q) П L“(Q),  k> 0  =^  Tk(v - w) G M(v).      (3.5)

Therefore, for every function v G T 0^{1 ,p} (Q), the set M(v) is nonempty.

Proposition 3.2. Let u be an entropy solution of problem (3.4) . Then, for every function w G M ( u ) , we have

Q

’i w ddx = / fw dx.

' Q

<1 Let v G W g^{1 ,p} (Q) П L “ (Q), and let k >  0. We define l = ^ v ^ l ^ (q) + 1. It is easy to find that there exists a sequence {v j } C C “ (^) such that v j ^ v strongly in Wj^Q), v j ^ v a.e. in Q, and, for every j G N, | v j | C l in Q. Since u is an entropy solution of problem (3.4), for every j ∈ N, we have

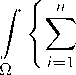
a i (x, u, 6u)D i T k (u

-

v j )

j dx C У

fT k (u - v j- ) dx.

By the properties of the sequence { v j } , we have

T k (u — v j ) ^ T k (u — v) a . e . in Q , T k (u — v j ) ^ T k (u — v) weakly in W₀ ^{1 ,p} (Q) . Using (3.7), we establish that

У fT k (u — v j ) dx ^

Q

У fT k (u — v) dx.

Q

(3.6)

(3.7)

(3.8)

(3.9)

Next, we fix i G { 1 , ... ,n} and define w i = a i (x,T k + i (u), VT k + i (u)). In view of (3.1), we have w i G L ^{p/ ( p- 1)} (Q). Then (3.8) implies that

У w i D i T k (u — v j ) dx ^

Q

У w i D i T k (u — v) dx.

Q

(3.10)

Using Propositions 2.1 and 2.2, we find that w i D i T k (u — v) = a i (x,u, 8u)D i T k (u — v) a.e. in Q and, for every j G N, w i D i T k (u — v j ) = a i (x, u, 8u)D i T k (u — v j ) a.e. in Q. Therefore, in view of (3.10), we have

У a i (x,u,8u)D i T k (u — v j ) dx ^

Q

У a _i (x,u,8u)D _i T k (u — v ) dx.

Q

This along with (3.9) and (3.6) implies that, for every v G W g^{1 ,p} (Q) П L ^ (Q) and every k >  0,

a i (x, u, 5u)D i T k (u

— v) d dx C У fT k (u — v) dx. ' Q

(3.11)

Now, let w G M(u). For every m G N, we define w _m = T _m (u) — w. We fix k >  ||w^l « (qj , and let m G N. Since w m G W 1^,p (Q) A L “ (Q), it follows from (3.11) that

a i (x, u, 5u)D i T k (u

-

w m )

j dx C У

fT k (u — W m ) dx.

(3.12)

Using Propositions 2.1 and 2.2, we find that, for every i G { 1 , ... ,n } ,

D i T k ^(u - w m ) = ⁽5 i u • l {| u | > m } + D i w) • 1 {| u - w m | } a . e . in ^Q .

This along with (3.2) and (3.12) implies that

У । ^ a i (x,u,6u)D i w > dx C У fT k (u — w m ) dx.

(3.13)

{| u - W m | } ^⁼¹                 J Q

It is easy to see that meas(Q \ {| u — w _m \ < k}) C meas {| u | > m } . Consequently, we have meas(Q \ {| u — w _m| < k}) ^ 0. In addition, T k (u — w _m ) ^ w a.e. in Q. Using these facts, we pass to the limit in both sides of inequality (3.13) and then, taking into account the arbitrariness of w G M(u), we obtain the required result. >

Remark 3.4. In the case of a class of degenerate anisotropic elliptic equations with L ¹ -data, a result similar to Proposition 3.2 was proved in [34] using, as here, an idea of [4, Corollary 4.3].

From Proposition 3.2 and implication (3.5), we deduce the following result.

Corollary 3.1. Let u be an entropy solution of problem (3.4) . Then, for every function v G W₀ ^{1 ,p} (Q) П L “ (Q) and every k >  0 ,

a i (x, u, 5u)D i T k (u

— v) d dx = / fT k (u — v) dx. ' Q

(3.14)

Remark 3.5. In view of Definition 3.1 and Corollary 3.1, u is an entropy solution of problem (3.4) if and only if u G T ^{1 ,p} (Q) and, for every function v G W₀ ^{1 ,p} (Q) П L “ (Q) and every k >  0, equality (3.14) holds.

4.    Estimates of Entropy Solutions

Let f : [0 , + to ) ^ R be the function such that, for every s G [0 , + ro ),

^f(s)= у^{|f 1} dx.

{I f IM

The function f is nonnegative, nonincreasing, and measurable. Using this function, we obtain some estimates for an entropy solution of problem (3.4). They are important for the proof of our main theorems in Section 5.

In what follows, we denote by C i , i = 1 , 2 ,..., positive constants depending only on n, p, c, and meas Q.

We define в=p -1 -T.

2 p - 1

Proposition 4.1. Let u be an entropy solution of problem (3.4) , and let k ^ 1 . Then

I k (u) <  ck [k ^-e + f k )],

(4.1)

(4.2)

meas {| u | >  k} <  c ₂ k q [k ^e + f (k) j ^n/(n p ) .

<1 By Definition 3.1 and Proposition 2.1, we have

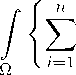
a i (x, u, ^T k (и))D i T k (u)

j dx <  У

f T k ( u ) dx.

Hence, using (3.2), we obtain the inequality cIk (u) <

(V^f

Q

f T k ( u ) dx.

(4.3)

We estimate from above the integral in the right-hand side of this inequality. It is clear that

I fT k (u) dx

Q

=

{| f 1 <к ^в }

fT k (u)

dx +

/

fT k (u) dx.

{| f l ^ k ^e }

Then, using the properties of the function T k and the definition of the function f , we get

J fT k (u) dx <  k ^e ^T k ( u ) \\ l i (q) + kf (k).                      (4.4)

Q

Since u E Tq’^p(Q), we have T k (u) E Wo ^,P (Q). Therefore, by (2.1),

II TkMb- (Q) « C n,p [I _k ( u )] ^{1 /p} .

Then, using the H¨older and Young inequalities, we obtain

\\T k ( u ) \\ l 1 (Q) <  C ₄|| T k ( u ) \ l _p - (q) ^ c ₅ [ I k ( u )] ^{1 /p} <  c , k ^{)/(p - 1)} +2 -^{1 - t} k       cI k (u).

This along with (4.3) and (4.4) implies the inequality

I k (u) <  c 1 [ k ^{p ( e + T )/(p - 1)} + k ^{1+ T} f (k ) ] .

Hence, taking into account the definition of β , we get inequality (4.1). In turn, Proposition 2.4

and inequality (4.1) yield inequality (4.2). О

We define

=    ^{в(п -} P)

Y в + n - 1 — т

Proposition 4.2. Let u be an entropy solution of problem (3.4) , and let k ^ 1 . Then meas> u | >  k} C C 3 k ^-r [k - + f (k - 1)] ^{n/ ( n- 1 -T} ) .                 (4.5)

<1 Let h: [1, +w) ^ R be the function such that, for every s G [1, +w), s h(s) = I s-1

f (t) dt.

Obviously, the function h is continuous. In addition, for every s G [1 , + ro ), we have

f(s) ^C h^{(s) C} f ⁽s - 1) .                                    ⁽4.⁶⁾

This is due to the fact that the function f is nonincreasing.

Now, let ф : [1 , + to ) ^ R be the function such that, for every s G [1 , + to ) ,

^ ( s ) = s ^{p ( n- 1 -T ) / ( n-p )} [ s ^-e + h(s ^e ) ^{] -p/ ( n-p )} .

It is clear that the function -0 is continuous, ^ (1) C k^p, and ^(s) ^ + ^ as s ^ + to .

Therefore, there exists l G [1, +to) such that ^(l) = kp. Hence, l = k(n-P)/(n-i-T) [re + h(ie)]1/(n-1-T), k-pl1+T [l-e + h(le)] = l-q [l-e + h(le)]n/(n-p).

In turn, by (4.7), k-pl1+T [l-e + h(le)] = k-r [l-e + h(le)] n/(n-1-T).

Next, by Proposition 2.5, we have meas{|5u| > k} C c^pl~p* [Ii(u)]p*/p + k-pIl(u).                   (4.10)

In addition, we deduce from (4.1) and (4.6) that

I i (u) C C 1 l ^{1+ T} [ l ^-e + h(l ^e ) ] -

This along with (4.8)–(4.10) implies that meas{|5u| > k} C c3k-r [l-e + h(le)]n/(n 1 T).

Note that, by (4.7) and the definition of y , we have k ^Y C l ^e . Then, using (4.6) and the fact that the function f is nonincreasing, we obtain

h(l ^e ) C f (l ^e - 1) C f (k - 1) .

This along with the previous two inequalities yields inequality (4.5). О

Remark 4.1. The function f was introduced in [10], where estimates similar to those in

Propositions 4.1 and 4.2 were established in the case т = 0.

5.    Limit Summability Results for Entropy Solutions

In this section, we prove our two main theorems on the limit summability of entropy solutions of problem (3.4) and then we give some corollaries of the second one on the belonging of entropy solutions to the limit space W Q^,r (Q) and, as a particular case, to the space Wj^Q).

Theorem 5.1. Assume that

+m

I s [ /МГ^Л" ^{-Р )} ds< + “ , 1

(5.1)

and let u be an entropy solution of problem (3.4) . Then u G L q (Q) .

<1 Let ^ : [1 , + to ) ^ R be the function such that, for every s G [1 , + w ),

f ( s ) = с[, ^{- 1} + ;           .

The function ϕ is positive, nonincreasing, and measurable. In addition, by (5.1), we have

+ ^

[    ds< + „ .

We also note that, by Proposition 4.1, for every k ^ 1, meas{|u|e > k} < k q/e^(k).

Therefore, by Proposition 2.6, we get | u | ^e G L ^q/e (Q). Hence, u G L ^q (Q). >

Theorem 5.2. Assume that

+m

У “ [ Л ⁵) ] ”/ ' ” ^{- 1-}") ds <  +^ю >                            (5.2)

and let u be an entropy solution of problem (3.4) . Then | 5u | G L^r (Q) .

< Let ^ : [1 , + ot ) ^ R be the function such that, for every s G [1 , + w ), ? ( > ) = C 3 [ s ^{- 1} + Ж] "^Л" — ^{1 -Т )} .

The function ϕ is positive, nonincreasing, and measurable. In addition, by (5.2), we have

+m

I ^И ds <  + „

We also note that, by Proposition 4.2, for every k ^ 1, meas

1 2 IM ^Y >  kJ <  k^-rh ^ ( k ) .

Therefore, by Proposition 2.6, we get | 5u | ^Y G L ^r / ^Y (Q). Hence, | 6u | G L ^r (Q). >

We note that Theorems 5.1 and 5.2 generalize Theorems 3.1 and 3.2 in [10] related to the case т = 0.

From Theorem 5.2 and Proposition 2.3, we immediately obtain the following result.

Corollary 5.1. Assume that r ^ 1 and that inequality (5.2) holds. Let u be an entropy solution of problem (3.4) . Then u G W q¹ '" (^) .

It is easy to see that if ε >  0 and f G L ^1+s (Q), then inequality (5.2) is satisfied. We now give a weaker condition guaranteeing that inequality (5.2) is satisfied.

Proposition 5.1. Let A >  (n — 1 — т ) /n , and let

f [ln(1 + | f | )] ^{( n- 1 -T ) /n} [lnln( e + | f D] ^A G L ¹ (Q) .

(5.3)

Then inequality (5.2) holds.

<1 We define F = f [ln(1 + | f | )] ^{( n- 1 -T ) /n} [lnln( e + | f | )] ^A . Let s > e . Assume that the set {| f I ^ s } is nonempty. Then, fixing an arbitrary x G {| f | ^ s } , we find that

| f ( x ) | С (ln s ) ^{- ( n- 1 -T ) /n} (lnln s ) ^-A | F ( x ) | .

Therefore, taking into account condition (5.3), we obtain f (s) С (lns)-(n-1-T)/n(lnlns)-AHFIIli(q).

Obviously, the same inequality holds if the set {| f | ^ s } is empty. Then, for every s > e ,

[ f' ( s )] ^{n/ ( n- 1 -T} ) <  (ln s ) ^{- 1} (lnln s ) ^{-An/ ( n- 1 -T} ) | F n (Q ' ^T )

This along with the inequality A >  ( n — 1 — т ) /n implies that inequality (5.2) holds. >

As a consequence of Corollary 5.1 and Proposition 5.1, we obtain the following result.

Corollary 5.2. Assume that r ^ 1 . Let A >  ( n — 1 — т ) /n , and let inclusion (5.3) hold.

Let u be an entropy solution of problem (3.4) . Then u G W q¹ '" (Q) .

Remark 5.1. Since 1 < p < n and 0 С т < p — 1, we have n — 1 — т > 0. Therefore, by the definition of r , we get r ^ 1  ^^ т С

n(p — 2) + 1

n — 1

This implies that if p < 2 — 1 /n , then the inequality r ^ 1 does not hold. We also note that if p ^ 2 — 1 /n , then

0 С

n ( p — 2) + 1

n — 1

< p — 1 .

Corollary 5.3. Assume that p ^ 2 — 1 /n and

n(p — 2) + 1

n — 1

(5.4)

In addition, assume that

+m

I s f ( s ) ] ^{( n- 1) / ( n-p )} ds< _{+ ro} .

(5.5)

Let u be an entropy solution of problem (3.4) . Then u G W o^{1 , 1} (Q) .

• <1 By equality (5.4) and the definition of r, we have r = 1. Moreover, equality (5.4) yields that n/(n — 1 — т ) = ( n — 1) / ( n - p ). This and (5.5) implies that inequality (5.2) holds. Then, by Corollary 5.1, we get the required conclusion. >

Corollary 5.4. Assume that p ^ 2 — 1/n. Assume also that equality (5.4) holds. Let A > (n — p)/(n — 1), and let f [ln(1 + |f |)](n-p)/(n-1)[lnln(e + |f |)]A G L1(Q).                      (5.6)

Let u be an entropy solution of problem (3.4) . Then u G Wj^Q) .

• < By equality (5.4), we have (n — 1 — т)/n = (n — p)/(n — 1). Then A > (n — 1 — т)/n and, by (5.6), f [ln(1 + |f|)]^(n-1-T)/n[lnln(e + |f|)]^AG L1(Q). In addition, equality (5.4) implies that r = 1. We now deduce from Corollary 5.2 the required conclusion. >

6.    Weak Solutions and Their Summability

The main result of this section provides conditions for the existence of a weak solution of problem (3.4) belonging to the space Wg ^,r (Q). We also give some corollaries of this result.

Definition 6.1. A weak solution of problem (3.4) is a function u G Wj^Q), such that:

• (i)    for every i G { 1 ,... , n } , a i ( x, u, V u ) G L 1 (Q);

• (ii)    for every function v G C “ (Q),

  

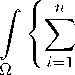
  a i ( x, u, Vu)D i v

  
  

  } dx = I

  Q

  
  

  fv dx.

  
  

Proposition 6.1. Assume that

τ<

n ( p — 2) + 1 n — 1

(6.1)

Let u be an entropy solution of problem (3.4) , and, for every i G { 1 ,..., n}, let a i ( x, u, 6u) G L 1 (Q) . Then u is a weak solution of problem (3.4) .

< Inequality (6.1) implies that 1 < r. Therefore, by Proposition 3.1, we have | ^u| G L 1 (Q). Then, using Proposition 2.3, we find that u G Wj^Q) and, for every i G { 1 ,..., n } , D i u = & i u a. e. in Q. Now, it is clear that, for every i G { 1 ,..., n } , a i (x, u, Vu) G L 1 (Q). In addition, we have C ^ (Q) C M(u). This and Proposition 3.2 imply that, for every function v G C “ (Q),

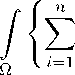
a i (x, u, Vu)D i v

dx =

Q

fv dx.

Thus, we conclude that the function u is a weak solution of problem (3.4). >

Remark 6.1. Since т ^ 0, inequality (6.1) can be satisfied only if p >  2 — 1 /n .

We now describe a particular case where any entropy solution of problem (3.4) is its weak solution.

Let p) G (0,pq/(p — 1)), let c >  0, and let g G L 1 (Q), ) ^ 0 in Q. We assume that, for almost every x G Q, every s G R, and every £ G R ⁿ ,

n

£ ^i( x,s,£ )r ^{/ ( p- 1)} <  )( | s | p + l £ l p ) + g ( x ) .                        (6.2)

i =1

By this, we make a restriction on the growth of the functions a i with respect to the variable s .

Proposition 6.2. Assume that

Г n(p - 2) + 1   p - 1 I т < min -----------,------— ,                       (6.3)

[ n — 1 n — p + 1 J and let u be an entropy solution of problem (3.4). Then u is a weak solution of problem (3.4).

• < 1 We first note that inequality (6.3) implies that inequality (6.1) holds. Next, we fix an arbitrary i G { 1 ,..., n } . By (6.2), we have

| a i ( x, u, 5u)l C c ^{( p- 1) /p} (| u | ^{p ( p- 1) /p} + |5u|^{p -1} ) + g ^{( p- 1) /p} a . e . in Q .           (6.4)

Since p(p — 1)/p < q, by assertion (a) of Proposition 3.1, we have u G L ^{p ( p— 1) /p} (Q). In addition, | ^u| G L ^{p- 1} (Q). Indeed, by (6.3), we have т < (p — 1) / ( n — p + 1). Hence, p — 1 < r. This and assertion (b) of Proposition 3.1 lead to the claimed inclusion for | δu | . Now, taking into account the inclusion g G L 1 (Q), we deduce from (6.4) that a i (x,u,8u) G L 1 (Q). Then, applying Proposition 6.1, we get the required conclusion. >

We note that Proposition 6.2 is a particular case of Corollary 3.2 in [18].

The main result of this section is the following theorem.

Theorem 6.1. Assume that т C min

( n(p — 2) + 1

[ n — 1

p — 1

n — p + 1

(6.5)

In addition, assume that inequality (5.2) holds. Then there exists a weak solution of problem (3.4) belonging to W Q^,r (Q) .

• <    As mentioned in Section 3, there exists an entropy solution u of problem (3.4). In view of inequality (6.5) and Remark 5.1, we have r ^ 1. Then, taking into account inequality (5.2), we deduce from Corollary 5.1 that u G W( 1 ^,r (Q). By (6.5), we have т C ( p — 1) / ( n — p + 1), which implies that p — 1 C r . Therefore, |V u | G L ^{p- 1} (Q). Moreover, in view of assertion (a) of Proposition 3.1, u G L ^ ^{p- 1) /p} (Q). Fixing an arbitrary i G { 1 ,... ,n } , by (6.2), we have

| a i ( x,u, V u ) | C c ^{( p- 1) /p} (| u | ^{p ( p- 1) /p} + |V u | ^{p- 1}) + g ^{( p- 1) /p} a . e . in Q .

This along with the above inclusions for u and |V u | implies that a i ( x, u, V u ) G L ¹ (Q). We also note that, by Theorem 5.2 and Proposition 2.3, we have 6u = Vu a.e. in Q. Then we conclude that, for every i G { 1 ,...,n } , a i (x,u,Su) G L 1 (Q). Hence, C “ (Q) C M ( u ). Therefore, by Proposition 3.2, for every function v G C “ (Q),

a i ( x, u, Vu)D i v

} dx = I

Q

fv dx.

Thus, we conclude that the function u is a weak solution of problem (3.4) belonging to W₀ ^{1 ,r} (Q). >

The following result is a direct consequence of Proposition 5.1 and Theorem 6.1.

Corollary 6.1. Assume that inequality (6.5) holds. Let A >  ( n — 1 — т ) /n , and let inclusion (5.3) hold. Then there exists a weak solution of problem (3.4) belonging to W^ r (Q) .

We give two other corollaries of Theorem 6.1.

Corollary 6.2. Assume that 2 — 1 /n C p C 2 and that equality (5.4) and inequality (5.5) hold. Then there exists a weak solution of problem (3.4) .

• < 1 Since p C 2, equality (5.4) implies that inequality (6.5) holds. In addition, by (5.4) and (5.5), inequality (5.2) holds. Then Theorem 6.1 leads to the required conclusion. >

Corollary 6.3. Assume that 2 — 1 /n C p C 2 and that equality (5.4) holds. Let A> (n — p)/(n — 1) , and let inclusion (5.6) hold. Then there exists a weak solution of problem (3.4) .

• <    By (5.4), we have ( n — 1 — т)/n = ( n — p)/(n — 1). This equality along with the inequality A >  (n — p)/(n — 1) and inclusion (5.6) implies that A >  (n — 1 — т)/n and that inclusion (5.3) holds. Therefore, by Proposition 5.1, inequality (5.5) holds. Then, by Corollary 6.2, we get the required result. >

Remark 6.2. The above corollary is a stronger result than Theorem 1.2 in [20] given for the case p = 2. Moreover, in the case 2 — 1 /n C p C 2, this corollary is a stronger result than Theorem 6 in [24], where it is required, as in [20, Theorem 1.2], that f ln(1 + | f | ) G L 1 (Q).

Finally, we give two corollaries of Theorem 6.1 which provide conditions for the existence of a weak solution belonging to the space Wq^,p 1 (Q).

Corollary 6.4. Assume that n > 2, p G (2,n), and p—1 т =---------.

(6.6)

(6.7)

n — p + 1

In addition, assume that

+m

I ¹ [ / ( s j j f n - p +D / f n - p ) ds< + _TO .

Then there exists a weak solution of problem (3.4) belonging to Wq^,p 1 (Q) .

• <    Since p >  2, equality (6.6) implies that inequality (6.5) holds. In addition, by (6.6), we have n/(n — 1 — т ) = (n — p +1) / ( n — p) and r = p — 1. The first of these equalities along with inequality (6.7) implies inequality (5.2). Now, applying Theorem 6.1 and using the equality r = p — 1, we obtain the required result. >

Corollary 6.5. Assume that n > 2 and p G (2 ,n ) . Assume also that equality (6.6) holds. Let A >  (n — p)/(n — p + 1) , and let f [ln(1 + | f | )] ( ^n-p ) ^/ ( ^n-p +¹) [lnln( e + | f | )] ^A G L 1 (Q) . Then there exists a weak solution of problem (3.4) belonging to W ^ 'p 1 (Q) .

• <    By the conditions of the corollary on т, A, and f, we have A > (n — 1 — т)/n and inclusion (5.3) holds. Therefore, by Proposition 5.1, inequality (5.2) holds. This along with the equality n/(n — 1 — т) = (n — p +1)/(n — p) implies inequality (6.7). Then, by Corollary 6.4, we get the required result. >

7. Examples

We first give an example of the functions a i satisfying conditions stated at the beginning of Section 3.

Example 7.1. Assume that p > 2, a G (2,p), т G [0,p — 1), and c > 0. Let b: R ^ R be a bounded continuous function such that, for every s G R, we have b(s) ^ c. In addition, let bo, bi: R ^ R be nonnegative continuous functions. Finally, let g be a nonnegative function in Lp/v 2)(Q). Now, for every i G {1,..., n}, let ai: Q x R x Rn ^ R be the function such that, for every triple (x, s, £) G Q x R x Rn, ai(X’S’$ = Wr-r + Ь1^ЖГ% + g(x)bo (s)^

• ⁽¹ + ^{|s| ) T}

Then the functions a i satisfy the growth, degenerate coercivity, and strict monotonicity conditions stated at the beginning of Section 3.

In the next example, we consider a function f G L ¹ (Q) satisfying inequality (5.2) and inclusion (5.3) for a suitable λ .

Example 7.2. Assume that Q = {x G Rn : |x| < 1/e}, and let a > 1. Let f: Q ^ R be the function such that f (0) = 0 and, for every x G Q \ {0}, f (x) = r4(lnn) • |x|n |x|

Since a >  1, we have f G L ¹ (Q). However, f G L ^{1+ e} (Q) for any e >  0. In addition, it is easy to verify that if s > e ⁿ , then f ( s ) C e n,_a (ln s ) ^{1 -a} , where в п,а is a positive number depending only on n and α . Then the following implication holds:

λ>

a — 1

= ^

+m

У ^_ [/( s ) ] ^A ds <  + “ .

Therefore, under the conditions p G (1 ,n ) and т G [0 ,p — 1), the inequality a >  2 — (1 + т ) /n implies inequality (5.2). Furthermore, under the same conditions on p and τ , the inequality a > 2 — (1 + т ) /n implies that, for every A >  (n — 1 — т ) /n , inclusion (5.3) holds. However, the inclusion f ln(1 + | f | ) G L 1 (Q) holds if and only if a >  2.