Constructing of OE-postman path for a planar graph

Great number of industrial branches is dealing with cutting the material such as metal, wood, plywood, glass and others. These materials are presented in industrial flow as sheets, boards, pipes, profiled rolls etc. Obviously, the usage of these materials implies their separation (or cutting) on parts of the given size and form (the samples of some details).

That is why the significance of industrial cutting is a source of economy and it is mentioned in technical literature and some industrial journals [1]. Theoretically this field is rather unexplored. There are some researches devoted to maximization of wood volume at lumbering process. The well known problem of circles placement on a plane is also similar to a cutting problem for an infinite sheet and equal round billets.

The experience of advanced engineering plants shows that accurate planning of cutting process allows to achieve the economy of materials [1].

Nowadays the problems of creation of the high-effective technologies of social sphere development, flexible automated enterprises on the base of information technologies, particularly, clothes production for individuals, particularly, the development of software for personified high quality clothes projecting for individual customer are actual. The brunch connected with flexible automated enterprises of consumer goods is officially called as one of prior branches of science development.

The interest to routing problems can be explained by their usage as mathematical models of different control problems and automation of projection. Particularly, for automated system of sheet material cutting process preparation the model of cutting plan can be presented as a planar graph. The aim of such modelling is a definition of the shortest path of a cutter. This path is to have no parts requiring any additional cuttings. However, to solve this problem one needs a formal statement in terms of a problem of path constructing as a planar graph. Due to the lack of a statement the algorithms of such rational trajectories definition should be developed.

One of the researches on special problems on graph theory is the monograph by Herbert Fleischner "Eulerian Graphs and Related Topics" [2,3] where some special types of Eulerian trails (for example, trails without forbidden transitions, А -trails, pairwisecompatible trails) are considered in rather detailed and systematised way.

There are also some papers of other authors where some problems on special type Eulerian trails are considered. For example, For example, the extension of forbidden transitions class [4], non-intersecting trails, bidirectional double paths [2,3], Petrie walks [5], straight-ahead walks [6], and edge-ordered paths [7] are among them.

Let’s solve the problem of constructing of the Eulerian trail with considered restriction as a cutting problem. Let the model of cutting sheet be presented as a plane S, and the model of cutting plan be a planar graph G with outer face f о on plane S. For any part J C G of this graph (a part of cutter movement trajectory) let's define by Int ( J ) a set-theoretic union of its inner faces (the union of all its connected components S \ J not containing outer face). Then Int( J ) can be interpreted as a part cut off a sheet. Let the sets of vertices and edges of graph J be denoted by V ( J ) and E ( J ) correspondingly, and IM| be a number of set M elements.

Let any path in graph G be considered as a part of graph consisting of all vertices and edges belonging to a path. This allows to formalize requirement to a cutter path as no intersection of inner faces of any initial path part for a fixed graph G with unpassed edges [8]. Let’s call such paths as ordered enclosing paths [9] (or OE -paths for short).

Int ( Ci ) П E ( G ) = 0

holds.

For example, let’s consider a plane Eulerian graph on fig. 1. Cycle

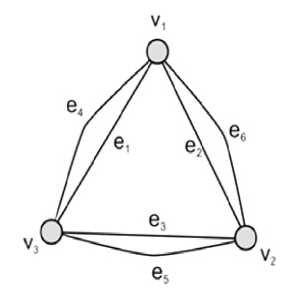
Fig. 1. Example of Eulerian graph v 1 e 1 v3e3v2e2v 1 e4v3e5v2e6v 1 satisfies the condition of ordered enclosing and cycle v 1 e4v3e5v2e6v 1 e 1 v3e3v2e2v 1 does not 1.>ecause Int (v 1 e4v2e5v3e6v 1) D {e 1, e2,e3}.

If a cutting plan is presented as plane Eulerian graph G then it can be passed without any additional (idle) cuts [10]. If this graph G is not Eulerian and has 2k odd vertices then it is possible to use Listing-Luke algorithm [2,3] to cover this graph by k trails. An algorithm for constructing of a cover with defined restrictions (OE-cover) is proposed in [11,12]. For an arbitrary chosen planar graph G the problem of OE-path constructing can be considered in terms of Chinese postman problem where a path to be defined consists only of graph G edges. Let’s consider this problem in details.

1. Algorithm Specification

Consider a planar graph G = ( V, E ) and a problem of constructing of a path C on the set of its edges E ( G ). To get a closed path we need some edges to be passed twice. Later we shall consider that edges passed twice are duplicated by additional edges belonging to set H ( G ).

Let’s show that algorithm for constructing of closed path P for non-Eulerian graph G be the algorithm for constructing of Eulerian OE -cycle C for Eulerian graph G being the modification of G received by addition of edges from set H ( G ).

Definition 2. A path C = v 1 e 1 v2e2 .. .v_k of graph G has an ordered enclosing (be an OE-path) if for any its initial part Ci = v 1 e 1 v 2 e 2 .. .ei, i <  ( |E ( G) | + |H ( G) | ) the condition

Int( Ci ) П ( E ( G ) U H ( G )) = 0

holds. I.e. the intersection of inner faces Ci with set of edges is empty.

In terms of cutting problem (for model of cutting plan as plane non-Eulerian graph) the edges of set H ( G ) are interpreted as idle passes of a cutter.

Using approach similar to Chinese Postman Problem one can define a set of edges to be duplicated. Obviously, the computing complexity of an algorithm may increase.

Here we shall add the duplicates in such a way that the recursive algorithm presented in [8] for Eulerian graphs will have less modifications. This modification can be as the following.

In the first part of algorithm when we need decision which edges bound the outer face it occurs that field Mark pointing to a next edge in this cycle consists of edge pointing on itself (terminal vertex of a current component) or this edge does not coincide with the initial one for this component and points to marked edges (bridge). In both cases one needs duplication of these edges. After adding these edges as it is shown on fig. 2 a) for a terminal vertex and on fig. 2 b) for a bridge some pointers are to be modified. By the way, each edge e E E of graph G is presented by pointers (functions) vi ( e ) (vertices incident to e ) and li ( e ) (adjacent edges-neighbours laying first in rotation of e around vi ( e )). i = 1 , 2.

After making such constructions the field Mark on a first stage of algorithm execution is to be formed such a way that all other functions for Eulerian graphs algorithm do not require any modifications. So, after adding all idle edges one has Eulerian graph, and a cycle found in it is to be an OE -cycle. That is why we have a path in initial graph where any cycle of passed edges does not contain inside any unpassed ones. Let’s call this modification of recursive algorithm as algorithm CPP_0E (see algorithm 5) (this algorithm solves the OE -Postman problem). The recursive call of function for each unmarked edge incident to vertices of a cycle received on a previous stage is made without changes. After constructing of a path for the considered component the path obtained is included to a resulting path.

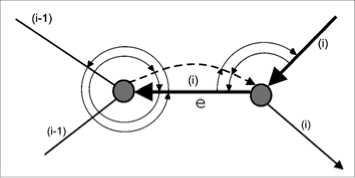
a)

б)

Fig. 2. Pointers modification after adding the edges: a) for a terminal vertex; b) for a bridge

Let’s generalize all above considerations as a following theorem.

Theorem 1. A path constructed by algorithm CPP_OE has to be an OE-path. The complexity of this algorithm is O ( IE ( G ) | ■ |И ( G ) | ).

The proof of this theorem is obvious because all additional edges are to be lacking parts of cycles determined by algorithm. We need less than O ( |E ( G)| ) edges additions, and each addition needs changing of four pointers (frictions).

Let’s organize the first part of algorithm as function ExternCycle (see algorithm 1) to make algorithm more descriptive. Input data for this function are:

e the first edge of a graph (it’s the edge from which the searching of edges bounding outer face of the current component starts);

e edge next to the starting one;

e the initial vertex for a currtnt component (for organising the correct edges orientation);

e some additional variables.

This function calls the process of edges addition in all considered above cases. The duplicating of a bridge occurs directly in a function ExternCycle, for the remained two cases of different modifications of function Add are called (see algorithm 3 and 4). The first one is used to drop-out the terminal vertex of a current component, and the second one is to finish a cycle in a current component.

The example of this algorithm execution is shown on fig. 3. The dashed line corresponds to the additional (idle) edges. The considered algorithm allows to find path v3v1v3v7v10v8v10v7v8v6v4v6v5v6v8v9v11v12v11v13v11v9v7v3v2v1v4v5v12v13v2.

Algorithm 1. ExternCycle (Part 1)

Require: G = (V, E) be a planar (graph where Ve G E the functions Vk(e) (vertices iundent to e) and lk(e) (edges iieighbouring to e received by its rotation counter-clockwise around Vk(e)). k = 1,2; First be the first considered edge: Next be a, pointer to the next edge: Vertex be a current vertex; Number be the number of edges in graph

Ensure: NewFirst be the number of additional edge finishing a cycle

procedure ExTERNCYGLE(In: G = ( V, E ), First, Next, Vertex, Number; Out: NewFirst) NewFirst = 0;

while true do

First = Next'. Vertex = v i( First ): Next = 1 1( First ):

if Mark(Next) = to then if Next = Start then if vi(First) = vi(Next) then

Add( G. Next. Mark ( Next )): Number = Number + 1;

Mark ( First ) = Number; Mark ( Number ) = Next:

Level ( First ) = L; Level ( Number ) = L. NewFirst = Number;

return NewFirst:

end if

Mark(First) = Next: Level(First) = L. return NewFirst: else e = 12( Mark (Next)):

if e = Start then while Mark(e) = to do e = 12( 11( e));

if e = Start then break;

end if end while end if if e = First then if Mark(Next) = to and Level(Next) = L then

Number = Number + 1;

v ₁ ( Number ) = v ₂( Next ): v ₂( Number ) = v ₁( Next ):

1 1( Number ) = 1 ₂( Next ): r ₁( 1 ₂( Next )) = Number;

r 1( Number ) = Next: 1 ₂( Next ) = Number;

if v 1( r 1( Next )) = v ₂( Number ) then

1 1( r 1( Next )) = Number;

else

1 2( r 1( Next )) = Number;

end if r2(Number) = r 1(Next); r 1(Next) = Number; 12(Number) = Next:

Next = Number:

end if

Next = e:

else

Number = Number + 1; A dd( G. Number. First):

Next = 1 ₁( First );

end if end if end if

Algorithm 2. ExternCycle (Part 2)

45:	if Vertex = v 2( Next ) then
46:	REPLACE ( Next);
47:	end if
48:	Mark ( First ) = Next: Leve1 ( First ) = L.
49:	if Next = Start then
50:	break;
51:	end if
52:	end while
53:	return NewFirst:

54: end procedure

Algorithm 3. Add (Function for adding of an idle edge for a terminal vertex)

• 1:    procedure ADD(In: G = ( V, E ) be a plan ar graph; Number be a number of additional (idle) edge; First be an edge leading to this terminal vertex)

• 2:     v ₁( Number ) = v ₂( First ): v ₂( Number ) = v ₁ (First ):

• 3:     1 1( Number ) = 1 ₂( First ): r i( Number ) = First:

• 1:      if v ₁ ( 1 ₂( First )) = v ₂( First ) then

5;         r i( 1 ₂( First )) = Number:

• 6:     else

7;         r ₂( 1 ₂( First )) = Number:

• 8:    end if

• 9:     1 ₂( First ) = Number:

• 10:     r ₂( Number ) = First:

• 11:      if v i( r i( First )) = v i( First ) then

• 12:         1 1( r i( First )) = Number:

• 13:      else

• 14:         1 ₂( r i( First )) = Number:

• 15:     end if

1G:     r i( First ) = Number: 1 ₂( Number ) = First: 1 i( First ) = Number:

• 17:    end procedure

Algorithm 4. Add (Function of adding of the idle edge for finishing a cycle)

• 1:    procedure ADD(In: G = ( V, E ) be a plan ar graph; Number be the number of added idle edge; Next be the edge belonging to an outer cycle)

• 2:     v i( Number ) = v ₂( Next ): v ₂( Number ) = v ₁( Next ):

• 3:     1 1( Number ) = Next: 1 ₂( Next ) = Number; 1 ₂( Number ) = Mark ( Next ):

• 1:     if v i( Mark ( Next )) = v ₂( Number ) then

5;        r i( Mark ( Next )) = Number:

• 6:     else

7;        r ₂( Mark ( Next )) = Number:

• 8:    end if

• 9:     r ₂( Number ) = Next: r i( Number ) = Next: r ₂( Next ) = Number;

• 10:    end procedure

Algorithm 5. CPP_OE (OE -chinese postman problem)

Require: G = (V, E) be a plan ar graph: Number Ire the number of graph vertices: First Ire a first considered edge

procedure CPP_OE(In: G = (V, E); Number', First; Out: Mark, Ret for all e E E do

Mark ( e ) = to:

end for

Start = Next = First:

NewFirst=ExternCycle (G. Start. Next. First. Vertex. Number}: Mst = 0; while true do if 12(Next) = First and Mark(12(Next)) = to then if Mst = 0 then

Mst = 1 2 ( Next ):

end if if v = v2(12(Next)) then

REPLACE! 1 2( Next )):

end if

Ret=CPP_OE ( G. 1 2( Next ). Number}:

if Mark ( First ) = to then

Mark ( First ) = 1 ₂( Next ):

else

end if end if

First = Next: Next = Mark ( First ): Vertex = v i( e ):

end if return Ret;

end procedure

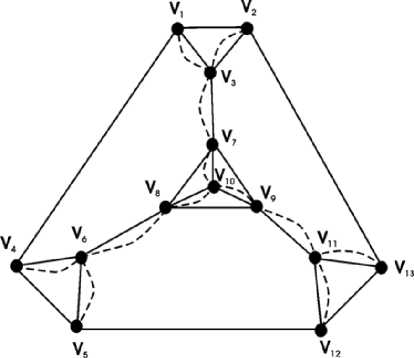
Fig. 3. The example of algorithm execution for a plane non-Eulerian graph

This algorithm allows to define |V | different paths for a given graph G. Here V is a set of graph G vertices adjacent to outer face of this graph. In fact it is only the low bound for number of solutions. However this algorithm allows to define only |V| of different solutions due to certainty of choosing of the next edge of the path.

• 2.    The Software for Constructing of Postman Pathwith Ordered Enclosing

Consider some examples demonstrating how the developed algorithm runs for non-Eulerian graphs. Figure 4 demonstrates the simplest example when graph has only two odd vertices (vertices 2 and 4) and both of them are adjacent to the outer face.

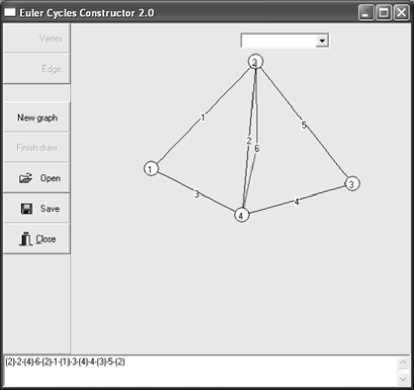
Fig. 4. One of the simplest examples of planar non-Eulerian graph

The additional (idle) edges are shown by a polyline. The significance of these idle edges is laid at a stage of model projecting (in terms of cutting problem they are understood, for example, as idle way of a cutter), not at a stage of solution finding. In a bottom of the window we see the defined path. Numbers of vertices are embraced.

For graph on fig. 4 algortighm constructs the additional edge 6 connecting vertices 2 and 4.

Consider the example of graph having no even vertices (see fig. 5).

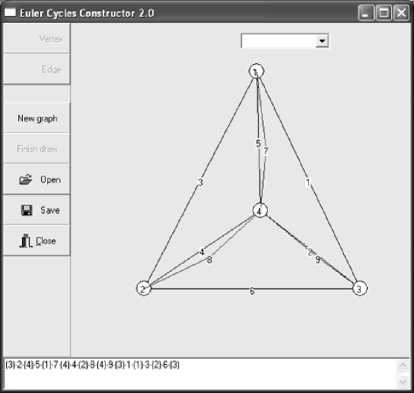
Fig. 5. Raph without even vertices

Obviously, after marking the outer cycle of edges 1, 3, and 6 we have a subgraph with three terminal vertices. To get an inner cycle we need a construction of three additional edges 7, 8, and 9. Such a construction is not optimal by the number of added edges because graph with four odd vertices needs only two additional edges to become Eulerian. Nevertheless, the received construction allows to get Eulerian graph while algorithm CPP_0E is running.

Consider more complex example (fig. 6) where one needs duplication of edges (that are bridges) not adjacent to exterior face.

Note that the condition of ordered enclosing holds because idle edges are the lacking parts of the inner cycles, and as the received Eulerian graph has an OE -cycle then a path where some edges are replaced by idle ones also has ordered enclosing.

Conclusion

The considered algorithm allows to find one of possible postman paths satisfying the condition of ordered enclosing corresponding to a chosen initial vertex. Algorithm has polynomial complexity. The developed software allows to solve the problem for an arbitrary planar graph. The software is tested for the typical cases of planar graphs. In all of these cases graph was completed to become Eulerian using considered above functions and OE- path for initial graph is defined.

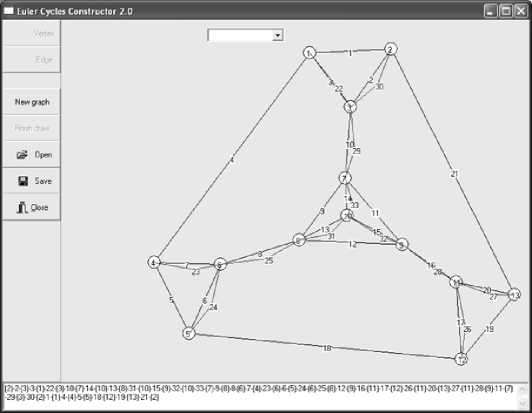
Fig. 6. Plane non-Eulerian graph where there are no planar matching of odd vertices