Деформационное состояние листа графена в рамках континуальной моментно-мембранной теории упругих пластин

Графен — это двумерный материал, представляющий собой монослой атомов углерода и обладающий уникальными свойствами [1] . Необычность графена проявляется не только в электронных, но и в механических свойствах. Графен является очень прочным, гибким материалом, который обладает выдающимися механическими характеристиками [2] : высокими модулем сдвига, модулем Юнга, продольной скоростью звука и другим.

При исследовании процессов деформирования однослойного листа графена (или других однослойных наноматериалов, например, однослойной нанотрубки) можно непосредственно рассматривать атомную или молекулярную природу строения этих наностуктур. Широкое распространение получило молекулярнодинамическое моделирование графена [3 –5] . На практике, для моделирования механического поведения графена или других двумерных наноматериалов, развит метод молекулярной механики (а также метод молекулярной структурной механики) [6 –10] и дискретно-континуальные модели [11 –15] .

При применении метода молекулярной динамики в основном предполагается, что между атомами двумерных наноматериалов имеют место силовые взаимодействия центрального характера. С этой точки зрения в работе [16] отмечается, что если в атомной модели однослойной нанотрубки (также для однослойного графена) учесть только силовое взаимодействие центрального характера между формирующими трубку атомами, тогда нанотрубка (или лист графена) не имела бы изгибной жёсткости и была бы неустойчива. Это означает, что только существование однослойной нанотрубки (или листа графена) будет свидетельствовать о необходимости учёта моментного взаимодействия между её атомами. Исходя из этого, далее, в работах [17 –20] , как континуальная модель деформационного поведения однослойной нанотрубки (а также однослойного листа графена), устанавливается трёхмерная моментная теория упругости с независимыми полями перемещений и вращений.

Так как графен и углеродная однослойная нанотрубка состоят из одного атомного слоя, следовательно, актуальной является проблема: для изучения механического поведения двумерных наноматериалов, необходимо

Статья опубликована в открытом доступе по лицензии CC BY 4.0

построение на основе трёхмерной моментной теории упругости адекватной двумерной модели пластин или оболочек. С этой точки зрения отметим, что в работе [21] сначала изучается линейная атомная цепочка, когда между атомами силовое взаимодействие нецентрально и также имеется моментное взаимодействие (для силового поля атомных взаимодействий выбран гармонический потенциал), а затем строится соответствующая её одномерно-стержневая континуальная модель. При рассмотрении ячейки периодичности кристаллической решётки графена взаимодействие между атомами заменяется указанными стержнями, в результате чего получается дискретно-континуальная (стержневая) модель графена и предельным переходом — его континуальная линейная модель. В этой же работе устанавливается, что построенная континуальная модель графена полностью идентична моментно-мембранной линейной теории упругих пластин [22, 23] и, при помощи сравнения этих двух моделей, определяются упругие жёсткостные характеристики указанной теории пластин через физические параметры гармонического потенциала углерода (которые в литературе известны).

Таким образом, моментно-мембранная линейная теория упругих пластин: а) плоское напряжённое состояние, б) поперечный изгиб, с определёнными указанным выше способом жёсткостными характеристиками, трактуется как континуальная теория деформаций графена, которая открывает большие возможности для изучения различных прикладных задач статики, динамики и устойчивости листа графена.

Возможно рассмотрение задач листа графена в его плоскости; для этого необходимо использовать модель плоского напряжённого состояния моментно-мембранной теории пластин. Аналогично, при его поперечном изгибе требуется применение модели поперечного изгиба указанной теории пластин. В данной работе для решения граничных задач плоского напряжённого состояния и поперечного изгиба моментно-мембранной теории упругих пластин разработаны варианты применения метода конечных элементов (МКЭ), которые дают возможность для изучения различных конкретных прикладных задач статики и собственных колебаний листа графена.

Отметим работы [24 –26] , которые посвящены применению МКЭ для решения различных прикладных граничных задач моментной теории упругости. Полученные численные результаты в работе [26] рассматриваются как дополнение к аналитическим решениям с позиций их использования для экспериментального подтверждения моментных эффектов при деформировании упругих материалов и в решении проблемы идентификации механических постоянных моментной теории упругости.

• 2.    Постановка задачи

В работах [22, 23] построена моментно-мембранная линейная теория упругих тонких оболочек (срединная поверхность оболочки отнесена к криволинейной ортогональной системе координат, в которой любой точке поверхности отвечают числа ( а 1 ,а ₂ ) ). Эта теория основывается на следующих гипотезах:

• 1)    кинематической: компоненты векторов перемещения ( V ) и свободного поворота ( ω ) не зависят от координаты z , которая отсчитывается по нормали от точки ( а 1 ,а ₂ ) срединной поверхности до произвольной точки оболочки:

V i = U i ( a i ,а 2 ) , V 3 = w ( a i ,a 2 ) (i =1 , 2); U k = П к ( a i ,a ₂ ) (k =1 , 2 , 3) ,                  (1)

то есть перемещения, прогиб, повороты распределены равномерно по толщине оболочки.

• 2)    статической: в физических соотношениях не принимаются во внимание напряжения как существенно меньшие: j ₃₃ — относительно напряжений ^ ii , где i = 1 , 2 ; a _{3 i} — относительно a _{i 3} ; моментное напряжение µ ₃₃ — относительно µ _ii ; µ _{3 i} — относительно µ _{i 3} .

• 3)    предполагается, что оболочка тонкая.

• 2.1.    Основные уравнения и граничные условия моментно-мембранной теории для случая плоского напряжённого состояния упругих тонких пластинок

Следует отметить, что решения трёхмерной граничной задачи моментной теории упругости в тонких областях, построенные в [27, 28] имеют свойства, отвечающие указанным гипотезам.

При переходе к рассмотрению пластинки из уравнений и граничных условий моментно-мембранной линейной теории упругих тонких оболочек [22, 23] , получаются две отдельные постановки, представляемые: 1) системой уравнений и граничными условиями для плоского напряжённого состояния упругих пластин, 2) системой уравнений и граничными условиями при поперечной изгибной деформации упругих пластин. Ниже приводятся обе системы уравнений и граничные условия в декартовых координатах x,y .

Основные уравнения и граничные условия, описывающие плоское напряжённое состояние упругих тонких пластин в рамках моментно-мембранной теории имеют вид [22, 23] :

– уравнения равновесия (движения, где t — время)

dT ii , dS 21     f d² U 1 \

∂x ∂y       ^{ρ 0} ∂t ^{2    ,}

dS 12 , dT 22     ^f 0 2 u 2 \

∂x ∂y      ^{ρ 0} ∂t ^{2 ,}

∂x

∂y

∂L 13 ∂L 23

1H( S 12 ∂x ∂y

S 21 )=o f j o ^d 2 S 3 ∂t ²

;

– геометрические соотношения

∂u1        ∂u2

r 11 =     , r 22 =     , r 12 ——

∂x        ∂y∂x

Ω 3 ,

Г 21 = du ¹ + '    k 13

∂y

∂Ω3

, k23 =;

∂x∂y

– физические соотношения упругости

~

~

^T 11 = ^Е * ^(Г 11 + ^vr 22 ) , T 22 = ^Е * ^(Г 22 + ^vr i1 ) ,

S 12 = C * ^[Г 12 + П 1 ^Г 21 ] ,

S 21 = C * ^{[ Г} 21 + П 1 ^Г 12 ^] ,

L 13 = B * ^k 13 ,  L 23 = B * ^k 23 ,  П 1

µ - α

^ + a ’

– граничные условия

—

—

—

x = const: T 11 = T 11 , S 12 = S 12 , L 13 = L 13 ; y = const:

S 21 = S — 21 ,

—

—

^T 22 = T 22 , L 23 = L 23

или

x = const: u 1 = u i , u ₂ = u ₂ , ^ 3 = ^ 3 ; y = const:

U 1 = — 1 , U 2 = U 2 , ^ 3 = ^ 3 ,

где чертой сверху отмечены заданные значения величин на контуре пластинки. Также могут иметь место смешанные граничные условия. В формулах (1) – (6) приняты обозначения: u 1 , u 2 — перемещения в плоскости ( x,y ) ; ^ ₃ — свободный поворот пластинки в плоскости ( x,y ) ; Г 11 , Г ₂₂ , Г ₁₂ , Г ₂₁ — тангенциальные деформации; k ₁₃ , k ₂₃ — изменения кривизны вокруг осей x,y соответственно; T ₁₁ , T ₂₂ , S ₁₂ , S ₂₁ — тангенциальные усилия hh

( T ii = f ^ ii dz , S ij = f G ij dz , i ^,j = 1 , 2 , i = ^{j )}; L 13 , L 23 — моменты относительно оси z от моментных напряжений - h            - h

h

M13, M23 (Li3 = f yi3dz, i = 1,2), распределённые вдоль осей x,y соответственно; p0 — поверхностная плотность -h материала пластинки; J0 — поверхностная плотность, мера инерции при вращении. В физических соотношениях (4) величины E∗, C∗, B∗ представляют собой жёсткостные характеристики плоской пластинки, которые связаны со свойствами её материала (E — модулем упругости, ν — коэффициентом Пуассона, µ, α, B — упругими постоянными пластинки) и с толщиной пластинки 2h формулами: E* = 2Eh, E* = E*/ (1 — v2), C* 2h(p + a), B* = 2Bh). В работе [21] для графена определены значения его жёсткостных характеристик (отметим, что для двумерных материалов удобно использование именно жёсткостных характеристик [20]). А это означает, что в континуальную модель графена (2)–(4) не требуется вводить числовое значение толщины пластинки, что является определённым преимуществом перед другими стандартными (классическими) моделями упругих пластин. Для численного расчёта пластинки графена с помощью МКЭ предполагается запись энергетического функционала, под которым в данной работе подразумевается выражение полной потенциальной энергии пластинки, состоящее из суммы потенциальной энергии деформации U и потенциала внешних сил и моментов V :

П = U — V,

где [23] :

U =

Wdxdy,

( S )

ab

V = У ( ^S 21 • ^u 1 + T 22 ^ ^u 2 + L 23 • ^ а)|   ^^dx + У ( Т 11 • ^u 1 + S 12 • ^u 2 + -£ 13 ’ ^ 3 ) |   ^У ■

Здесь W — поверхностная плотность потенциальной энергии деформации пластинки:

¹       22   22                     22   22                       2    2

W =2 р* (^Г11 ^{+ Г} ₂₂ ^{+2 vr} 11 ^r 22) ⁺ C * (^Г₁₂ ^{+ Г} ₂₁ ⁺² П 1 ^Г 12 ^Г 21) ^{+ B} * \^к 3 ₃ ^{+ k} ₂ 3) J .

Итак, имеем функционал для анализа плоского напряжённого состояния пластинки из однослойного графена в рамках моментно-мембранной теории упругих пластин. С математической точки зрения решение системы уравнений (2) – (4) с граничными условиями (5) , (6) эквивалентно отысканию минимума функционала (7) с учётом соотношений (8) – (10) [23] .

Следует отметить, что модель плоского напряжённого состояния моментно-мембранной теории упругих пластин идентична модели плоской задачи моментной теории упругости [29, 30] . Здесь эта модель относится к графену (с известными жёсткстными характеристиками). При а = 0 , B = 0 модель (2) - (6) переходит к плоскому напряжённому состоянию пластин как в классической теории упругости.

• 2.2.    Основные уравнения и граничные условия моментно-мембранной теории для случая поперечного изгиба упругих тонких пластинок

Описание поперечного изгиба упругих тонких пластин в рамках моментно-мембранной теории включает [22, 23] :

– уравнения равновесия (движения)

dN i3 + dN 23 ∂x ∂y

/ d ² w \    dLn dL 2i             / d ² ^ i \

-q³ <^{P o} dtfi / ~xr ⁺ ~y^ ⁺ N ²³ = ^-m1 J ⁰    /

∂L 12	∂L	∂ 2 Ω 2
∂x	+ -- N 13 = ∂y	m 2 J 0 dt 2

где q 3 , m 1 , m 2 — распределённые в плоскости пластины нормальная нагрузка и моменты-пары; – геометрические соотношения

Г 13 = dw + « , , ∂x

∂w          ∂Ω 1        ∂Ω 2        ∂Ω 2        ∂Ω 1

• ²³ dy 1 ,     11~ 9x’     22 dy ,    ¹² dx'    ²¹ dy ’

  – физические соотношения упругости

N 13 = D * r i3 , N 23 = D * r 23 , L 12 = D ‘ [ k i2 + П 2 к 21 ] , L 21 = D ‘ [ k 2i + П 2 к 12 ] ,

L 11 = ^D ' ^[(1+² n 2 ^{) k} 11 + П 2 ^к 22 ^] , L 22 = ^D ‘ ^[(l+² n 2 ) ^k 22 ⁺ П 2 ^к 11 ^] , П 2 = ⁽ 7 * ^{— e} * ^)/( 7 * + ^£ * )i

– граничные условия x = const: N13 = N13, L11 = L11, L12 = L12 или w = w, Q1 = ^1, ^2 = ^2;           (14)

y = const: N 23 = N 23 , L 21 = L 21 , L 22 = L 22 или w = w, ^ 1 = ^ 1 , ^ 2 = ^ 2 .            (15)

Здесь чертой сверху отмечены, величины заданные на контуре пластинки. Также могут иметь место граничные условия смешанного типа. В формулах (11)–(15) обозначено: w — прогиб срединной поверхности пластинки; Ω1 , Ω2 —свободные повороты точек пластинки относительно осей x и y; Γ13, Γ23 — поперечные сдвиговые деформации вплоскостях (x,z) и (y,z); k11, k22, k12, k21 —компоненты тензора изгиба-кручений; N13, N23 —перерезывающие hh усилия (Ni3 = f ai3dz, i = 1,2); L11, L22, L12, L21 —изгибающие и крутящие моменты (Lij- = f ^ijdz, i,j = 1,2); -h                                                                          -h

D * , D ‘ ( D * = 2 Gh , D' = 7 * + e * = ( 7 + e ) • 2 h) — жёсткостные характеристики материала пластинки при поперечном изгибе (при этом G — модуль сдвига, γ и ε — упругие постоянные моментной теории упругости, 2 h — толщина пластинки). Указанные жесткостные характеристики для графена определены в работе [21] .

Сформулированная граничная задача (11) – (15) , согласно моментно-мембранной теории поперечного изгиба упругих пластин [23] , эквивалентна вариационной задаче, имеющей в основе принцип возможных перемещений. Решение задачи в вариационной форме сводится к минимизации функционала полной потенциальной энергии пластинки размерами a x b :

П =

^Wodxdy — ^qwdxdy

a

( S )                ( S )

J ( N ₂₃ • w + L 22 • ^ 2 + L 21

x |y = b

• ^1     dx— y=0

b

У ( N 13 • ^w + ^L 11 ^ ^ 1 + ^L 12 ^2 ) |   (dy,

где поверхностная плотность потенциальной энергии её деформации W 0 выражается как

W 0 = 2 { D * ( ^Г 23 + ^Г ₂з ) + D ‘ [ ⁽¹ + ² П 2 ) ( k ll + ^k ₂₂ ) + ² n 2 k 11 k 22] + D ‘ ( ^k 12 + ^k 21 + 2 П 2 ^к 12 ^к 21 )} . ⁽¹⁷⁾

Отметим, что модель поперечного изгиба моментно-мембранной теории упругих пластин в силу того, что по толщине пластинки все искомые величины (1) распределены равномерно, при обращении в нуль моментной жёсткостной постоянной D ^′ не переходит в модель классической теории изгиба пластин. Однако эта модель, с математической точки зрения, аналогична модели изгиба пластин с малой сдвиговой жёсткостью, то есть модели пластин типа Тимошенко [31] . Это означает, что обе модели описываются одинаковыми уравнениями, но физические уравнения содержат различные коэффициенты.

• 3.    Конечно-элементное решение краевых задач статики и собственных колебаний в рамках моментномембранной теории упругих пластин на примере прямоугольного листа графена при плоском напряжённом состоянии и при поперечном изгибе

  • 3.1.    Задача статики

В рассматриваемых задачах действительные поля переменных сообщают минимум функционалу полной потенциальной энергии. Для задачи плоского напряжённого состояния (модель А) функционал задаётся выражениями (7) – (10) , для задачи поперечного изгиба (модель Б) — выражениями (16) , (17) . В рамках основных процедур МКЭ будем отыскивать приближение к точному решению для обеих граничных задач.

После разбиения прямоугольной срединной поверхности на прямоугольные конечные элементы полная потенциальная энергия пластинки представляется в виде:

П =

mm

X n e = x (2    ^

e =1       e =1 _s e

m

X/ a-1

l ^e

U ^T p ^e dl ^e ,

где s ^e — площадь конечного элемента, l ^e — его контур, m — общее число элементов, ε ^T , σ , U ^T , p ^e — векторы переменных, T — символ операции транспонирования.

Модель А. Плоское напряжённое состояние пластинки. В этом случае величины, входящие в (18) , выражаются через следующие параметры элементов: { e e } ^T = ( Г^ ,Г 1₂ ,Г ₁ ^е ₂ ,Г 2₁ ,k e ₃ ,k e ₃) — вектор обобщённых деформаций, { ^ e } ^T = (Tf^T ^ e S^S^L^ Le)} — вектор обобщённых усилий, { u e } T = ( u ! ,u 2 ,^ ₃) — вектор обобщённых перемещений, { p e } T = ( Tie^ S^jL^ )) — усилия на контурах x = const прямоугольного элемента, { p e } T = ( S 2 ₁ ,T2 2 ⁾ ,L 23) ) — усилия на контурах y = const прямоугольного элемента. Символ T указывает на операцию транспонирования.

Рассмотрим равновесие некоторого элемента e с узлами i, j, k, l , каждый из которых характеризуется 9 степенями свободы (9 независимыми переменными): u ⁽ ₁ ^e) , u ^(e) , Ω ₃ ^(e) ∂ u ⁽ ₁ ^e) /∂ x , ∂u ^(e) /∂x , ∂Ω ₃ ^(e) /∂x , ∂u ⁽ ₁ ^e) /∂y , du ^(e) /dy , d^ ^(e) /dy . Представим переменные u 1 e ) , u ^(e) , ^ ^(e) в плоскости { x,y } в виде полиномиальных рядов, содержащих в общей сложности 36 коэффициентов α 1 ,α 2 ,...,α 36 :

• u 1 e ) = а ₁ + а ₂ х + а з у + а 4 Х ² + а 5 у ² + а б ху + а 7 Х ² у + а 8 ху ² + а 9 Х ³ + а ₁о у ³ + a ₁₁ x ³ y + а ₁₂ ху ³ , u 2 e = а 1з + а 14 х + а 15 у + а 1б Х ² + a 17 y ² + a 18 xy + a 19 x ² y + a^xy ² + ацх ³ + ацу ³ + а 2з х ³ у + a 24 xy ³ , ⁽¹⁹⁾ ^ ⁽²⁾ = а 25 + a 26 x + a 27 y + a 28 x ² + a 29 y ² + а зо ху + а з1 Х ² у + а з2 ху ² + а зз х ³ + а з4 у ³ + а з5 Х ³ у + а зб ху ³ .

После выполнения процедур МКЭ придём к соответствующим дискретным представлениям:

{ u e } =[ N ] {Н , К} =[ R ][ N ] {П =[ В ] {П , К} =[ D ][ B ] { ^ ² } ,               (20)

где [ N ] — матрица базисных функций конечного элемента (матрица функций формы), [ R ] — матрица дифференциальных операторов, связывающих линейные деформации и деформации изгиба–кручения с перемещениями и свободным поворотом, [ D ] — матрица упругости:

	д / дх	0	0		1-    ~ E ∗	E ∗ ν	0	0	0	0
	0	д/ду	0		E ∗ ν	E ∗	0	0	0	0
[ R ] =	0	д/дх	- 1	, [ D ] =	0	0	C ∗	C ∗ η 1	0	0
	д/ду	0	1		0	0	C ∗ η 1	C ∗	0	0
	0	0	д / дх		0	0	0	0	B ∗	0
	0	0	д / ду		0	0	0	0	0	B

Далее вектор узловых обобщённых перемещений в элементе e выражается через искомые переменные:

e }T = G. "     d e ue. "  e д ■      d^ ei д^    ^д ■ ^д       du j du j     d£ j dn j

1i, ∂x , ∂y , 2i, ∂x , ∂y , 3i, ∂x , ∂y , 1j, ∂x , ∂y , 2j, ∂x , ∂y , 3j, ∂x , ∂y e ∂ue1k ∂ue1k ue ∂ue2k ∂ue2k Ωe ∂Ω3ek ∂Ω3ek ue ∂ue1l ∂ue1l ue ∂ue2l ∂ue2l Ωe ∂Ω3el ∂Ω3el 1k, ∂x , ∂y , 2k, ∂x , ∂y , 3k, ∂x , ∂y , 1l, ∂x , ∂y , 2l, ∂x , ∂y , 3l, ∂x , ∂y .

Модель Б. Поперечный изгиб пластинки. При поперечном изгибе входящие в выражение полной потенциальной энергии пластинки (18) обобщённые параметры связываются с характеристиками конечных элементов, которые отвечают состоянию поперечного изгиба: { u ^e } ^T = (w e ,^ e ,^ e ) — вектор обобщённых перемещений, { e e } T = ^{(г е} 3 ^,г 2 > 3 ^,к 1 1 ^к 2 ,^ ^— вектор обобщённых деформаций, ^{ ff ^e } ^T = ⁽ N e 3 ,N e 3 ,L 1 ₁ ,L e_!2 ,L 1 ₂ ,L 2 ₁ ^{) —} вектор обобщённых усилий, { p ^e } T = ( N e ₃ ,L 11) ,L 12) ) — усилия на контуре x = const прямоугольного элемента, { p e } T = (N 23 ,L 21 L 2 ) — усилия на контуре y = const прямоугольного элемента.

Узлы прямоугольного конечного элемента также имеют по 9 степеней свободы ( w e , ^ e , кД дw^e/дх , dw ^e /dy , д^ е /дх , д^ е /ду , d^ e /дх , д^ ^ /ду) . Прогиб w e и независимые повороты n e , ^ e представляются подобно (20) :

w = а 1 +а ₂ х+а з у + а 4 х ² + а 5 у ² + а б ху + а 7 х ² у + а 8 ху ² + а 9 х ³ + а 1о у ³ + а 11 х ³ у + а ₁₂ ху ³ , ^ 1 = а 13 + а 14 х + а 15 у + а 1б Х ² + а 17 у ² + а 18 ху + а 19 х ² у+а 2о ху ² + а 21 Х ³ + « 22 у ³ + а 23 х ³ у + а 24 ху ³ , ^ 2 = а 25 + а 2б х + а 27 у + а 28 х ² + а 29 у ² + а 3о ху + а 31 Х ² у+& 32 ху² + а 33 х ³ + а 34 у ³ + а 35 х ³ у + а 3б ху ³ .

В этом случае также приходим к дискретным выражениям вида (20) , где на этот раз

	д/дх	0	+1	D ∗		0	0	0	0	0
	д/ду	- 1	0		0	D ∗	0	0	0	0
[R] =	0	д /дх	0	,    [D] =	0	0	D ‘ (1 + 2 n 2 )	D ′ η 2	0	0
	0	0	д / ду		0	0	D ′ η 2	D (1+2П 2 )	0	0
	0	0	д / дх		0	0	0	0	D ′	D ′ η 2
	0	д/ду	0		0	0	0	0	D ′ η 2	D ′

Вектор узловых обобщённых перемещений в элементе e связан с другими узловыми переменными:

= ( w e д< д< _П.   ■      _П.          w e         _П.   ^ ^> _П .

i , ∂x , ∂y , 1i, ∂x , ∂y , 2i, ∂x , ∂y , j , ∂x , ∂y , 1j, ∂x , ∂y , 2j, ∂x , ∂y , we ∂wke ∂wke Ωe ∂Ω1ek ∂Ω1ek Ωe ∂Ω2ek ∂Ω2ek we ∂wle ∂wle Ωe ∂Ω1el ∂Ω1el Ω(e) k, ∂x , ∂y , 1k, ∂x , ∂y , 2k, ∂x , ∂y , l , ∂x , ∂y , 1l, ∂x , ∂y , 2l ,

_{∂Ω 2}( e _l ) _{∂Ω 2}( e _l ) ∂x ^, ∂y

.

Далее, для задач А и Б, исходя из функционала (18) , после дифференцирования в соответствии с МКЭ [32 –34] и введения обозначений:

{ f e } = / [ N ] T { p ^e } dl e , [ K e ] = JJ[B] T [D][B]ds e ,

( l ^e )

( s ^e )

придём к уравнению равновесия элемента e :

e

— = [Ke]{Se}-{f e} = 0, где [Ke] — матрицы жёсткости конечного элемента e, {fе} — вектор эквивалентных узловых сил.

Далее, объединим эти элементарные матричные соотношения в одно матричное соотношение, в которое внесём изменения в целях учёта кинематических граничных условий (при представлении вектора узловых сил статические граничные условия выполняются автоматически), получим окончательную систему алгебраических уравнений:

[Kdw = {fP}, порядок которой соответствует числу введённых в рассмотрение неизвестных. Матрица KP носит название глобальной матрицы жёсткости, {fP} — глобального вектора узловых сил системы, а {Д} — глобального вектора узловых неизвестных:

{ Д } = {2,.../n}^t.

Здесь: N — общее число узлов в системе; δ i — вектор неизвестных i -го узла вида (21) или (22) .

• 3.2.    Задача собственных колебаний листа графена

Решение этой задачи также будем находить численно, с помощью МКЭ.

При исследовании собственных колебаний пластины по модели А функционал (7) – (10) заменяется лагранжианом:

L 2   2              2   2              22

1 = 2    [* (^Г 11 + ^Г 22 + 2 ^vr ii ^r 22) +C * \Г 2 2 + ^Г 21 + ² П 1 ^Г 12 ^Г 21) + B * У 13 + + ^k ₂ 3J \dxdy~

- 2 ^2// ^ Р 0 ( u 1 + u 2 ) ⁺ J o ^ ² ] dxd^y’                                (25)

( s )

где ω — круговая частота колебаний. В случае модели Б функционал (16) , (17) заменяется лагранжианом вида:

L 2 — x   { D * ( ^r 13 + ^r 23 ) + D [ ⁽¹+² П з ) (^кп + ^к ₂₂ ) +2П 2 ^1^22 ] + D ( k ₁₂ + к ₂₁ +2П 2 • k i2 k 2i\ ] dxdy —

( S )

- 2 ^ 2 Ц [ p o w ² + J o ( ^ 2 +Q 2 )]dxdy,                           (26)

( S )

Экстремальные свойства (см. [35] ) функционала (25) или (26) приводят в задаче на собственные колебания к следующим конечно-элементным уравнениям для элемента:

{[K e]-w2[M e]Hn—0, где [Ke] — матрица жёсткости (23), [Me] — матрица массы конечного элемента e. Глобальная система однородных алгебраических уравнений метода МКЭ в целом для пластины примет вид:

{[ K P ] -M' — 0 ,                         (27)

при этом [KP] —глобальная матрица жёсткости, [MP] —глобальная матрица масс, { 4 } — глобальный вектор узловых неизвестных (24) . В системе (27) необходимо учесть кинематические граничные условия.

Система (27) является задачей на собственные значения, решениями которой служат частоты и формы собственных колебаний пластины в рамках моделей А и Б листа графена.

• 4.    Результаты решения задач

Рассмотрим задачи статики и собственных колебаний прямоугольного листа графена по модели Б (поперечный изгиб пластинки) (Рис. 1) при двух вариантах закрепления по контуру: 1) шарнирное опирание; 2) жёсткое защемление. В задаче статики зададим q3 = const, m1 — 0, m2 — 0. Первый вариант граничных условий записывается так:

x — 0 ,a : w — 0 , —2 —0 , ^ 1 — 0; dx

y — 0,b : w — 0 , ^ 2 — 0 , 1 — —0 . dy

В расчёте использовались характеристики графена из [21] (размерности содержат приставку «н» — нано: наноНьютон (нН), нанометр (нм) и так далее): D * — 86 нН/нм; D ' — 0 . 415 нН^нм; п ₂ — - 0 . 219 . Для q ₃ принималось значение: q ₃ —10 ^-3 нН/нм ² . Пластинка графена имела размеры 0 — 20 нм, b — 20 нм.

Из решения матричного уравнения (27) с учётом граничных условий (28) получим значения всех искомых величин в любой точке прямоугольной области. Таблица 1 содержит вычисленные значения компонент обобщённых переменных в центральной точке D ( a /2 ,b /2) прямоугольной области размерами a х b . Для сравнения здесь и в последующих таблицах приведены точные значения, определённые из решения граничной задачи методом двойных тригонометрических рядов.

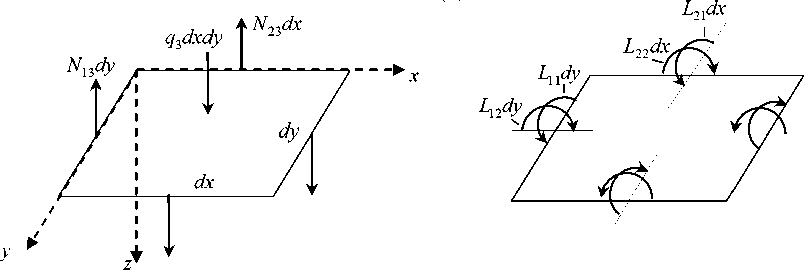
Рис. 1. Распределённые усилия ( а ) и моменты ( б ) в элементе пластины при расчёте по модели Б

Таблица 1. Значения компонент обобщённых переменных в центре прямоугольной области

Компонента	Число конечных элементов в дискретизирующей область сетке				Точное значение
	4	16	36	64
Прогиб w , нм	0.1019	1.1214	1.4664	1.5231	1.5665
Свободный поворот Ω 1 , рад относительно оси x	0	0	0	0	0
Свободный поворот Ω 2 , рад относительно оси C	0	0	0	0	0
Перерезывающее  усилие N 13 , нН/нм	0	0	0	0	0
Перерезывающее усилие N 23 , нН/нм	0	0	0	0	0
Крутящий момент L 11 , нН	0	0	0	0	0
Крутящий момент L 22 , нН	0	0	0	0	0
Изгибающий момент L 12 , нН	0.0023	0.0156	0.0182	0.01817	0.01775
Изгибающий момент L 21 , нН	–0.0023	–0.0156	–0.0182	–0.01817	–0.01775

Таблица 2. Значения компонент обобщённых переменных в точке с координатами B ( a,b/2)

Компонента	Число конечных элементов в дискретизирующей область сетке				Точное значение
	4	16	36	64
Свободный поворот Ω 2 , рад относительно оси y	0.0133	0.1786	0.2391	0.2504	0.2598
Перерезывающее усилие N 13 , нН/нм	–0.0597	–0.0377	–0.0144	–0.0086	–0.0067
Крутящий момент L 11 , нН	0	0	0	0	0
Изгибающий момент L 12 , нН	0	0	0	0	0

Таблица 3. Наименьшая частота собственных колебаний листа графена

Наименьшая частота собственных колебаний	Число конечных элементов в дискретизирующей область сетке			Точное значение
	4	16	36
ω , ГГц	19.5	6.47	5.80	5.72

Результаты решения задачи на собственные колебания прямоугольного листа графена приведены в таблице 3 ( р ₀ = 0 . 76 • 10 - 15 нкг/нм ² ; J 0 = 0 . 46 • 10 - 19 нкг [21] ).

Данные таблиц 1–3 демонстрируют сходимость численного решения к точному с измельчением конечноэлементной сетки.

Рассмотрим задачу при втором варианте граничных условий:

x = 0 ,a : w = 0 , Q 1 =0 , Q 2 = 0;

x = 0 ,b : w = 0 ,   12 1 =0 ,   12 2 = 0 .

При 64 конечных элементах получены следующие результаты: w ( O ) = 0 . 478 нм; 12 1 ( O ) = 12 2 ( O ) = 0 ;

N 13 ( O ) = N 23 ( O ) = L ii ( O )= L 22 ( O )=0 ; L 12 ( O ) = 0 . 00897 нН; L 2i ( O ) = - 0 . 00897 нН; w =10 . 9 ГГц.

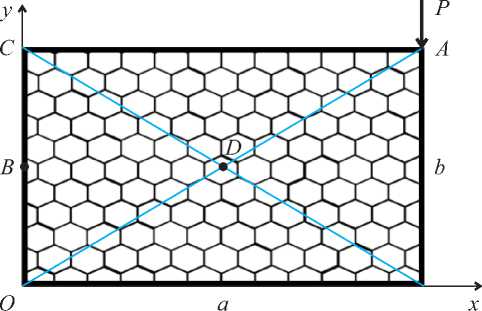
Рис. 2. Расчётная область в задаче плоского напряжённого состояния прямоугольного листа графена

Теперь рассмотрим задачи статики и собственных колебаний прямоугольного листа графена по модели А (плоское напряжённое состояние). На рисунке 2 показан прямоугольный лист графена с контрольными точками. Левый конец этой области жёстко защемлён, в точке A приложена сосредоточенная нагрузка P . Граничные условия этой задачи имеют вид:

x = 0: u 1 =0,u ₂ = 0 ,^ 3 = 0

y = 0: S 21 = 0 ,T 22 = 0 ,L 23 = 0 ,

У = b: S21 = 0,T22 = -P6(x-a,y) L23 =0, x = a : S12 = 0, T11 = 0, L13 = 0, где S(x,y) — дельта-функция Дирака.

Расчёты выполнены при значениях параметров: E * = 287 нН/нм; E * = 304 нН/нм; C * = 168 нН/нм; B * = 0 , 505 нН•нм [21] , a = 20 нм, b = 20 нм, P = 0 , 5 нН. В результате вычисленный получены следующие данные в точках A (a,b) , B (0 ,b /2) при w = 93 ГГц: u 1 ( A ) = 0 . 0115 нм, u ₂ ( A ) = - 0 . 0226 нм, П 3 ( A ) = - 0 . 00481 рад, T 11 (B) = - 0 . 0014 нН/нм, S ₁₂ ( B ) = 0 . 00328 нН/нм, L ₁₃ ( B ) = 0 . 00014 нН.

• 5.    Заключение

На основе построенной в рамках моментно-мембранной линейной теории упругих тонких пластин континуальной математической модели деформационного поведения листа графена представлен его конечно-элементный расчёт в случае задач статики и собственных колебаний. Использован четырёхузловой прямоугольный конечный элемент с характерными узловыми кинематическими параметрами, отвечающими моментно-мембранной теории упругих тонких пластин. При вариационной реализации метода конечных элементов для задач статики листа графена получены матрицы жёсткости и векторы эквивалентных узловых усилий, а для задачи собственных колебаний — матрица жёсткости и матрица масс. С использованием разработанного алгоритма конечно-элементного подхода решены и проанализированы прикладные задачи статики и собственных колебаний листа графена при его плоском напряжённом состоянии и поперечном изгибе. Численные результаты демонстрируют достаточно хорошую сходимость. Построенные конечно-элементные соотношения обладают универсальностью и могут применяться при решении других задач с наноструктурами в рамках моментно-мембранной линейной теории упругих оболочек.

Работа выполнена в рамках контракта N: 10-12/23-I/SHSU, финансируемого Комитетом по науке Республики Армении.