Design of Fast Pipelined Multiplier using Modified Redundant Adder

Published Online April 2012 in MECS

• I.    INTRODUCTION

  The circuits for arithmetic operations like adder and multiplier have long propagation time delay, limited range of bits and complexity in hardware. RBSD numbers is gaining much attention due to carry free addition property and thus fast addition[1,2]. The computation time also depends upon the suitable circuit design[3]. Therefore it is highly desirable to construct efficient digital logic circuit. In 2006, N. Sharma proposed the adder cell design using universal logic gates for fast

addition[5]. In this paper the adder cells are modified and which further used for the computation of high speed adder and multiplier circuit.

Multiplication is the repetitive addition of the partial products[6,7]. The partial products generated can be reduced by applying RBSD booth’s encoding technique [8]. The concept of pipelining is desirable to speed up the operation[9,10]. Therefore for the fast multiplication, reduced number of partial products are added simultaneously using proposed adder cell structure and addition is carried out in pipelined structure due to which the entire ALU operation can be fast.

This paper emphasizes briefly about the RBSD addition in section 2. The concept of fast adder cell using universal logic is described in the sections 3. Section 4 gives comparison among the previous and proposed cell structures. An implementation and comparison between CLA and RBSD adder upto 64 bit is made in section 5. Idea to design fast multiplier with the concept of pipelining is given in section 6. Finally in section 7 implementation and comparison of Wallace Booth Multiplier (WBM) and pipelined RBSD Multiplier is presented.

• II.    RBSD Addition

  Avizienis[1] in 1961 proposed RBSD number system in which the digit set (1, 0, 1 ) is used to represent numbers. The decimal value of RBSD number can be calculated by following relation.

Let the number (10)10 can be represented in binary as

1010 while in RBSD it can be represented by more than one way i.e. 1 1 1 1 0 or 1 1 0 11 0. These redundant representations of numbers gives technique of carry free arithmetic.

Adder is the basic building block for the computation of all mathematical operations. Hence a carry free addition technique is desirable which achieved using following equations[1].

These equations 2-4 gives the result of addition in three steps. There was no carry propagation chain as at the last stage of computation the digit w i ’’ and t i ’’ both never 1 or 1 simultaneously. A number of any bit length can be added in constant time period.

The digital systems do not support the -1 logic therefore for the logic circuit design of RBSD Adder, Kal

and Rajashekhar, 1990 has given following Boolean expressions 5-9[11].

d i   = m , ®_ X i+ X i" ® y i+ yf                    (5)

m i+1 = x i + y i+                                           (6)

b i+1 =  m i x i+ x i- + x i+ y i+ +  y i+   y i- m i

+ x i+ x i- y i+ y i-                                 (7)

s i+ = d i _ b i                                                  (8)

s i- = d i b i                                                     (9)

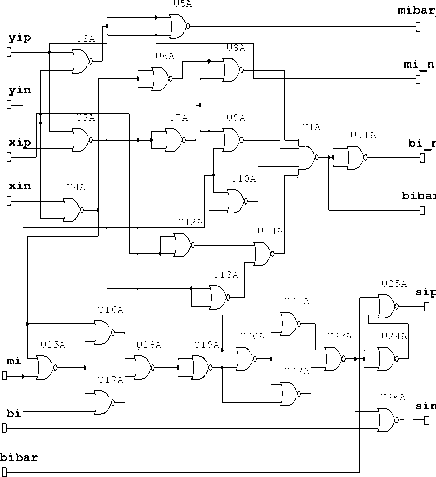
Figure 1. RBSD Adder Cell: NOR-NOR Logic

Here m i , b i and d i are binary variables with digit set {0,1} and x_i ⁺ x_i ^- , y_i ⁺ y_i ^- are RBSD input numbers and s_i ⁺ s_i ^- output sum in RBSD with digit set (-1,0,1) represented by binary encoded form i.e. (0,1), (0,0), (1,0) respectively.

• III.    Fast Adder Design

  N Sharma et. al. in 2006 designed the adder cells by

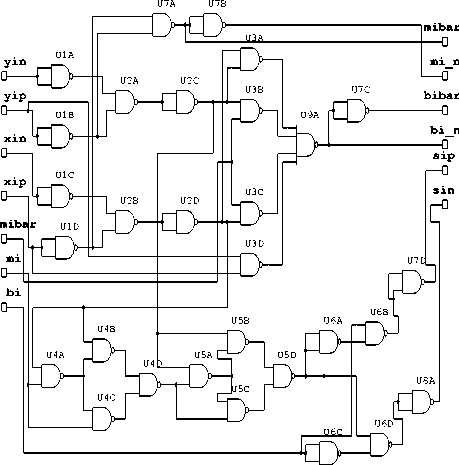
Figure 2. RBSD Adder Cell: NAND-NAND Logic.

TABLE I. variable used

+ xi+ xip ■ xi xin + yi+ yip ■ yi yin mi mibar m i+1 mi_n mi+1 mibar_n bi bibar b i+1 bi_n bi+1 bibar_n universal logic gates using equations 5-9[5]. The logic circuit design using these gates is desirable due to uniformity in the circuit and these circuits are inexpensive in manufacturing aspects and preferred by the logic designers. Keeping above aspects adder cell was designed using NOR-NOR logic and NAND-NAND logic as shown in figure 1 and 2 respectively. In these logic diagram the various inputs and outputs used from equations 5-9 are expressed as per table I. This cell was designed to add 1 bit RBSD number and the same circuit connected in parallel can be used to add n bit numbers. The delay time of these adder cells found less as compared to the previous adder cell developed using basic logic gates and suggested by Kal and Rajshekhar [11].

Proposed Adder Cell design

A modification has been made in the architecture of universal logic adder cell structure by reducing the gate count. The reduction in gate count is due to redesign of part of the circuit which is giving intermediate output d i . This output is produced through XOR gate as given in equation 5.

If A, B, C are the input bits and Y is output then the logic equation for 3-input XOR gate will be

Y = A ⊕ B ⊕ C

(Let A, B, C input and Y output)

=

The above logic equation can be implemented using 4 AND and 1 OR gate. This logic equation can also be implemented using either 6 NOR gates or 5 NAND gates by replacing equivalent universal logic implementation of

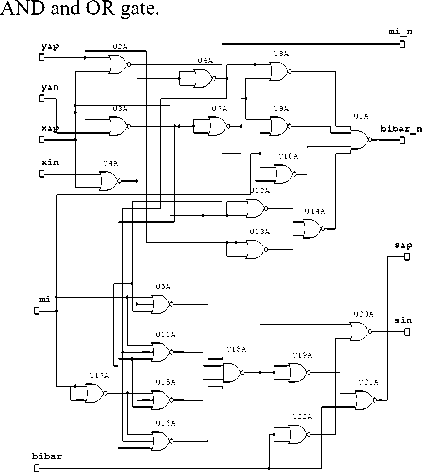
Figure .3. Modified Cell: NOR-NOR logic and after 2 logic levels as shown in fig 4. One more NAND gate is reduced due to no need of signal mi_n for further stages in modified design.

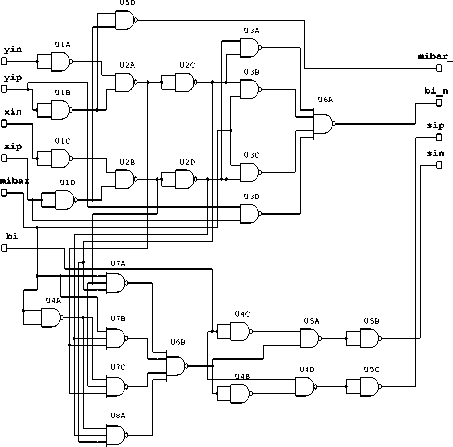
Figure 4. Modified Cell: NAND-NAND logic

Hence the output d i produced by 3-input XOR gate have been achieved after 10 NOR gates (U15A to U24A) and passing the signal over 8 logic levels in the adder cell designed by N Sharma using NOR-NOR logic as shown in figure 1. But in proposed modified design the same output can be achieved using 6 NOR gates (U5A, U11A, U15A, U16A, U18A and U19A) only and crossing the 3 logic levels as shown in fig 3 [4]. Similarly the output d_i in NAND-NAND adder cell proposed by N Sharma shown in fig. 2 has been achieved after 8 NAND gates (U4A, U4B, U4C, U4D, U5A, U5B, U5C & U5D) and passing the signal over 7 logic levels. But in proposed modified design the same output can be achieved using five NAND gates (U7A, U7B, U7C, U8A & U6B) only Hence the Modified adder cell has been designed using reduced number of NOR or NAND gates.

• IV.    Comparison of various Adder Cell

Hardware

Figure 5 and Table II shows a clear comparison among the circuit shown in figure 1, 2, 3 and 4. It is clear that the modified architectures are better as the numbers of inputs are less as compared to other cell structures. Further the number of gates required in proposed designs is also less. To get the final output, the input crosses less levels in proposed design.

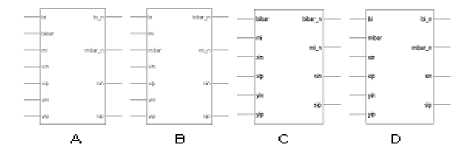
Figure 5. Block diagram representation of adder cell (A) NOR-NOR (B) NAND-NAND (C) modified–NOR (D) modified-NAND

T able II. C omparative A nalysis among various adder cells

Type of Adder Cell	Total NOR / NAND Gate used	Required I/P Signals	Levels Crossed to get O/P
			si +	s i-
NOR-NOR	26	7	9	8
Modified NOR-NOR	22	6	6	6
NAND-NAND	30	7	11	10
Modified NAND-NAND	26	6	8	8

Simulation Result

All the modified Adder cell architectures are verified using Multisim software and their timing reports are generated on Xilinx project navigator.

T able III. T ime D elay

RBSD Adder Cell Type	Time Delay (ns)
NOR-NOR	11.861
Modified NOR-NOR	11.807
NAND-NAND	11.978
Modified NAND-NAND	11.861

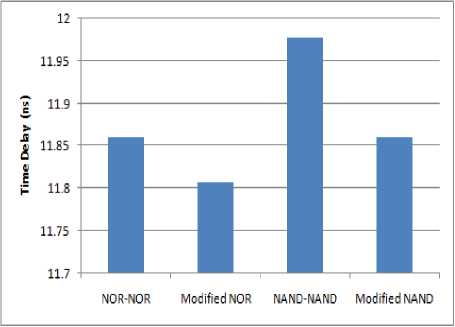
Figure 6. Time delay in different architectures of Adder cell

The FPGA implementation of these circuits is made on Spartan II XC2S50-5pq208. It is clear from the table III and figure 6 that the propagation delay time to get the addition result for one bit addition is less in modified architectures as compared to previous.

• V.    Implementation of CLA and modified RBSD Adder

In this section the VHDL implementations of Carry Look Ahead (CLA) Adder[12] and RBSD adder of n-bit is simulated on modelsim simulator and synthesized on xilinx project navigator and their timing reports were observed for various values of n up to 64 bits.

A comparative graph between CLA and RBSD adder is shown in figure 7. It is observed that the delay produced in RBSD adder is high compared to CLA initially as the number of bits are less but as the number of bits increases CLA adder takes more time but in RBSD time remains constant which is very less for any number of bit additions. In CLA the add time increases gradually due to logic for carry calculation and hence hardware circuit changes with increase in bits.

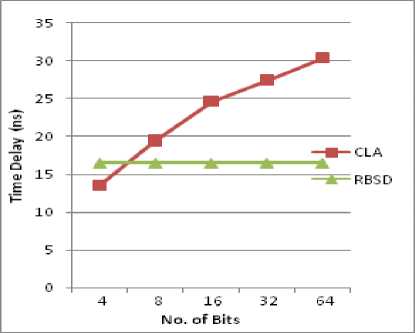
Figure 7. Timing comparison among CLA and Modified RBSD Adder

Hence for higher bit length, RBSD adders are suitable due to carry free addition and same adder cell structure is used for the addition of any bit number.

• VI.    Fast Multiplier Design

Multiplication is the most critical operation in every computational system. It is the repetitive addition of partial products. It involves two basic operations [7].

• 1.    The generation of partial products

• 2.    Their accumulation to produce the final product.

Hence for speeding up the multiplication process firstly there should be reduction in number of partial products generated which can be achieved by Booth’s encoding technique [6,8]. Secondly the time needed to add these partial products which can be achieved by using the carry free SD pipelined adders. This approach reduces the delay time immensely instead of carry save adder. The steps for multiplication are detailed below. Take two binary numbers one multiplicand and other multiplier.

• 1.    Convert the multiplicands from two’s complement form to RBSD representation (multiplier is retained in two’s complement form).

• 2.    Generate n/2 RBSD partial products using Booth’s bit-pair recoding technique on the n-bit two’s complement multiplier and the RBSD multiplicand.

• 3.    Add the partial products pair wise by means of a binary tree of log 2 (n/2) levels of RBSD adders.

• 4.    Convert the resulting RBSD product into two’s complement form.

As per the steps the multiplicand is converted into two’s compliment form and then to RBSD form. Multiplier is also converted to 2’s compliment form and then the partial products are generated as per Booth Bit pair recoding technique.

The partial products are added simultaneously using RBSD adders to generate the partial product sums. Log2 (n/2) levels of RBSD adders are required to obtain the product in RBSD. Finally the product is converted to 2’s compliment form using CLA adder.

Pipelined design

The 16 x 16 fixed-point multiplication units can be divided into six pipeline stages as shown in figure 8. Stage S1 generates the partial product and stage S2 converts the partial products to RBSD numbers. Stages S3, S4 and S5 add the RBSD numbers. Here it is important to note that since RBSD adder delay time is independent of word length with increased complexity, stages S3, S4 and S5 will have the same delay time. Stage S6 is a CLA adder used to convert the RBSD number in two’s complement form.

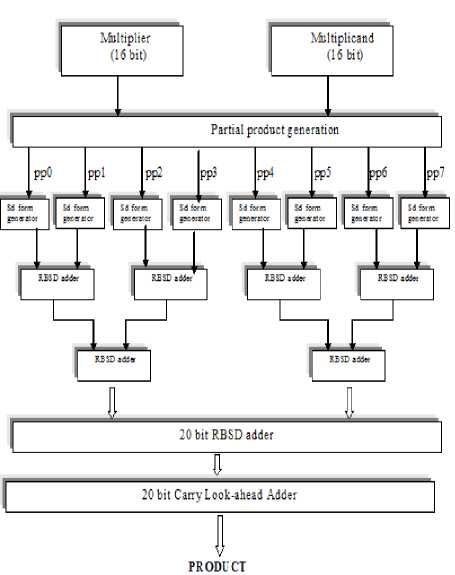
Figure 8. Block Diagram for multiplication of 16 x 16 bits.

Delay times of stages S1, S2 and S6 can be further adjusted. The pipeline is thus divided into six stages and the clock rate can be fixed as desired to give appropriate results. The pipeline unit for 16x16 bit multiplication is shown in figure 8. Fast addition techniques i.e. Booth’s encoding, addition of partial product using modified cell and pipelining will help in increasing the processing speed [9],[14].

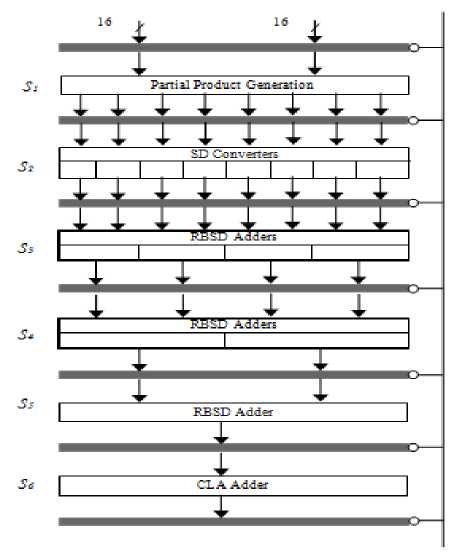
Figure 9. Pipeline unit for fixed-point multiplication of 16x16 bit numbers.

• VII.    Implementation and timing analysis of Pipelined multiplier with WBM

Pipelined RBSD multiplier and Wallace Booth multiplier (WBM) upto 16x16 bit length was simulated and synthesized using VHDL. The software used for simulation was FPGA Advantage and that for synthesis was Xilinx Project Navigator.

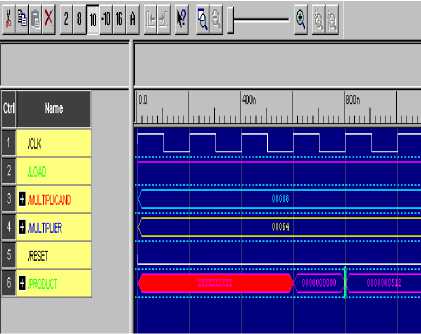
Figure 10. Simulation Result of Pipelined Multiplier Comparison of WBM and RBSD multiplier

Simulation output after multiplication is shown in figure 10 and timing analysis between WBM and RBSD Multiplier is shown in figure 11. The working of multiplier is also verified using field programmable gate array XC2S50-5pq208.

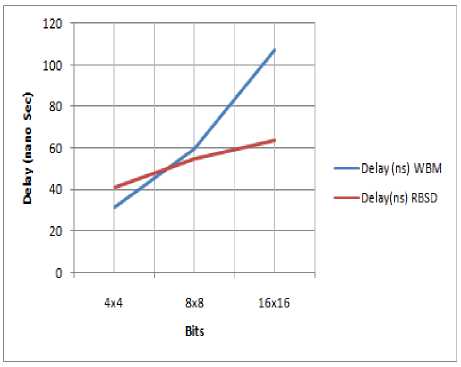
Figure 11. Comparison between WBM and RBSD Multiplier

• VIII.    Conclusion

The delay time of the adder cell has been reduced in the modified architectures using NOR-NOR logic and NAND-NAND logic. The number of gate counts has been reduced in the proposed adder cell and hence overall reduction in number of logic levels and inputs will also reduce the circuit complexity.

The efficiency of RBSD adder increases as bit length of the summands increases. The higher the bit length, the efficiency of RBSD adder is high as compared to CLA. The delay time of RBSD multiplier is reduced using the pipelined design and fast RBSD adder cell for the addition of partial products. It is concluded that delay time of multiplication is less in RBSD multipliers as compared to Wallace Booth Multiplier and verified by the result of synthesis due to carry free addition using modified adder cell and pipelining.

Finally addition is the base for all the mathematical operations[13],[15],[16] like division, reciprocation, square rooting, inverse square rooting etc., fast arithmetic processor of higher bit length can be designed using proposed architectures of adder cell. Therefore the proposed modified RBSD adder cell is highly appreciable for the design of ALU of higher bit length. The new designs will be simpler, fast and will consume less power.