Детектирование дефекта в металлических объектах транспортной инфраструктуры в зависимости от частотного спектра ультразвуковых волн при использовании систем неразрушающего контроля

В настоящее время для решения различных задач дефектоскопии объектов транспортной инфраструктуры (ОТИ) достаточно часто используют установки с использованием активного эхо- импульсного метода (эхо- метода), подразумевающего излучение и приём ультразвуковых волн (УЗВ) [0 -0] .

К основным недостаткам относят: необходимость разработки спецметодик диагностики для конкретных типов изделий и наличия мертвых зон‚ которые снижают эффективность диагностики. Кроме того, необходимо отметить, что иногда дефектоскопия на базе УЗВ может и не дать точного ответа о реальном размере дефектов, так как детектируется только их отражательная способность в направлении приемника. Хотя размер и отражательная способность коррелируют, но не для любых классов дефектов.

Способ возбуждения УЗВ в системах дефектоскопии базируется на использовании пьезоэлектрического эффекта. В этом случае генерация УЗВ происходит при помощи обратного пьезоэлектрического эффекта, то есть электрические колебания преобразуются в акустические. Отраженные УЗВ, после прохода исследуемого объекта и призмы, падают на приёмную пьезопластину пьезоэлектрического преобразователя (ПЭП) и, благодаря прямому пьезоэлектрическому эффекту, преобразуются в электрические, регистрирация которых происходит при помощи соответствующих измерительных цепей.

В основном применение систем дефектоскопии связано с возможностью применения методов неразрушающего контроля (НК) твердых объектов разных размеров [0]. Эти методы особенно эффективны при обнаружении различных дефектов, таких как поры, небольшие трещины и т. д.

Существующие системы дефектоскопии на базе УЗВ применяют ПЭП с прямым или наклонным лучом (НЛ). Отличие состоит в том, что в установке с НЛ присутствует специальная призма, которая обеспечивает падение упругих волн под требуемым углом на поверхность исследуемого изделия. Коэффициент затухания УЗВ материала, из которого изготовлена призма, достаточно большой. Это необходимо для быстрого затухания не вошедшей в изделие УЗВ.

Методы НК с НЛ применяются в ситуациях, когда при прямолинейном контроле поиск дефектов становиться достаточно сложным. Например, тонкие вертикальные трещины могут быть не обнаружены ввиду их малого отражения.

Работа системы НК с НЛ базируется на нескольких физических явлениях, а именно. При падении ультразвуковой волны (УЗВ) на границу раздела двух сред, каждая из которых обладает своим акустическим сопротивлением, часть энергии будет отражена обратно в первую среду. Оставшаяся часть энергии перейдет в другую среду. Необходимо отметить, что акустическое сопротивление влияет не только на отражение и поглощение, но и на излучение и распространение УЗВ. При этом характер отражения и преломления УЗВ существенным образом зависит от угла между направлением распространения волны и нормалью к поверхности раздела сред (угла падения). Следовательно, на границе раздела призма/исследуемый объект про- исходит трансформация УЗВ одного типа в УЗВ другого типа, благодаря чему на границе в общем случае возникают две отраженные и две преломленные УЗВ, распространяющиеся в разных направлениях.

ПЭП, входящий в состав системы НК с НЛ, обычно генерирует частоты от 1 до 10 МГц, которые определяются подаваемым на ПЭП краткосрочным электрическим импульсом, вырабатываемым генератором зондирующих импульсов. Выбор диапазона частот является компромиссом между наличием эффекта отражения УЗВ от дефекта с одной стороны, и быстрым затуханием УЗВ с другой. ПЭП крепится к линзе через соответствующий согласующий слой. Кроме того, с нерабочей стороны ПЭП содержится защитный слой, который называют демпфирующим блоком. Он служит для создания однонаправленного излучения.

Задача компьютерного моделирования распространения упругих волн в процессах контроля изделий ОТИ, в частности с использованием систем НК с НЛ, является актуальной. Это связано с тем, что ее решения позволяют проектировать системы НК с НЛ с необходимыми характеристиками, обеспечивающих эффективный контроль, и как следствие, повышение технической безопасности изделий ОТИ.

Постановка задачи

В данной работе рассматривается модель установки НК с НЛ в соответствии с рис. 1. Математическая модель (ММ) НК при помощи УЗВ должна служить базой для:

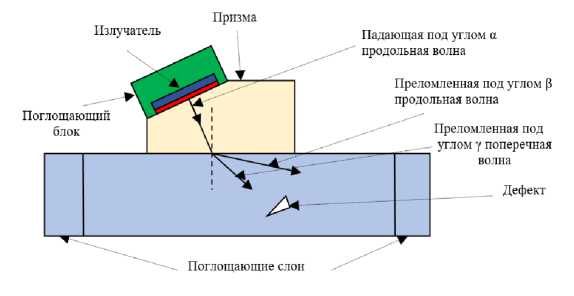
Рис. 1. Модель установки неразрушающего контроля с наклонным лучом.

• 1.    Моделирования процесса возбуждения УЗВ и их распространения в заданной среде.

• 2.    Моделирования процесса рассеяния волн на дефекте.

Также ММ должна включать основные черты следующей физической модели, которую можно описать следующим образом. Система НК с НЛ расположена на алюминевой пластине недалеко от дефекта. Актуация одиночного модельного импульса будет производиться от ПЭП. Дефект расположен на пути преломленного импульса. Основные этапы процесса работы системы НК НЛ следующие. От ПЭП запускается модельный импульс, который, попав в призму, распространяется в ней в виде волны давления. Дойдя до границы, призма/исследуемый объект, она преломляется, попадает в исследуемый элемент, преобразуется в сдвиговую волну, которая доходит до дефекта и рассеивается на нем, отражается, и проделав обратный путь, попадает на приёмную пьезопластину ПЭП.

Основные задачи, решение которых необходимо получать в ходе вышеописанного процесса следующие: анализ типа волн, возбуждаемых в исследуемом элементе, выделение волн сдвига, обработка которых является основной для системы НК с НЛ, оценка отражённого импульса.

Необходимо отметить, что в данной работе не рассматривается процесс восстановления изображения дефекта.

Частоту УЗВ необходимо задавать исходя из задачи исследования. При поиске дефектов в исследуемом объекте принято использовать УЗВ от 0.25 до 25 МГц. Но на практике, верхнюю границу обычно ограничивают 14 МГц.

Кроме того, при моделировании необходим учет следующих фактов. УЗВ на частотах 0.25–1 МГц слабо рассеиваются. Но так как угол раскрытия пучка УЗВ на этих частотах большой, то их применение для поиска небольших дефектов нецелесообразно. Для детектирования дефектов небольшого размера следует применять УЗВ на частотах 2–6 МГц. В этой ситуации угол раскрытия пучка достаточно небольшой, а лучи образуют пучок иглообразной формы, достаточно сильно рассеивающий на границах исследуемого изделия. Поэтому их следует выбирать только для небольшого радиуса действия, несмотря на то что их проникающая способность велика. При выборе УЗВ выше 6 МГц на практике возникают сложности, заключающиеся в том, что в этом случае пьезоэлементы являются тончайшими кристаллическими пластинками, легко разрушающимися от механических воздействий.

Компьютерное моделирование для решения задачи анализа применения УЗВ разной частоты в конкретной системе НК НЛ для определения заданного дефекта в исследуемом объекте с определенными характеристиками позволяет разрабатывать методики и рекомендации для контроля изделий ОТИ. Это моделирование базируется на математическом аппарате описания распространения УЗВ в линейноупругих средах [0 ,0] .

В данной работе распространение возмущения для каждого блока представлено волновым уравнением в следующей форме [0] :

Р--V- S + У, — = F - ХР

¹ a t      (       ¹ a t J ^{1     11}

P -1 (V v+(v v) T ) = 0

S = CE где v - скорость возмущающегося воздействия, pi - плотность материала i - го блока, S - тензор напряжений, E - тензор деформаций, С - тензор упругости (или жесткости) и Fi - сила, действующая на i - тый блок, у, Xi - коэффициенты демпфирования и сопротивления для i – го блока.

Начальные условия выбираются из физических соображений. Например, в начальный момент времени излучатель не генерирует УЗВ. Поэтому и возмущающие воздействия отсутствуют во всех блоках.

Физическая интерпретация (1) выглядит следующим образом.

Продольная волна, распространяющаяся в призме из акрилового пластика со скоростью c = 2080 —, падает под углом p1 с а = 28° на исследуемый аллюминиевый образец. После этого происходит разделение этой волны на отраженую в призму, и преломленную в исследуемом образце в виде продольной (под углом в) и поперечной (под углом у) волны. Скорость распространения продольной УЗВ в аллюминии c = 6200 м, поперечной c = 3120 м.

p2             с                             2

Углы в и у определяются по закону

Снеллиуса [0] :

sin а  sin в sin

=      =

С лС p1          p 2

УЗВ, дойдя до дефекта или границ исследуемого образца, отражаются, и проде- лывают обратный путь до ПЭП с соответствующей трансформацией в призме.

Компьютерное моделирование проводилось для разных значений центральной частоты: f 0 = [1,0; 1,5; 2,0; 4,0; 8,0] МГц.

Актуация сигнала соответствует формуле:

U_o • e ~⁴⁽ tf ⁰ - ^{2 )} • sin ( 2 пf^t ) .

Амплитуда U _o = 200 вольт.

Решение (1) проводилось при помощи разрывного метода конечных элементов Галеркина (dG-FEM) [0] . В этом методе применяется дискретизация 4 порядка. Следовательно, можно ограничиться величиной размера конечного элемента равной f 0 /1,5.

Результаты компьютерного моделирования

Компьютерное моделирование проводилось с использованием системы MATLAB, применяемой для решение различных задач [0 -0] . Моделирование проводилось для образцов с дефектом и без. На Рис. 2 представлены сигнал напряжения на выходе ПЭП преобразователя для исследуемых образцов с (зеленый) и без (синий) дефектом при f 0 = 1 МГц.

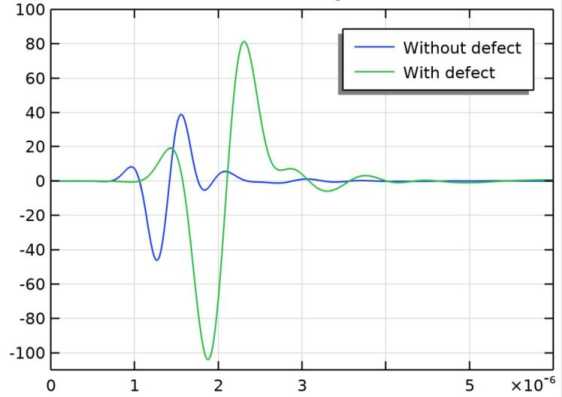
Рис. 2. Сигнал напряжения на выходе ПЭП с f 0 = 1 МГц

Ось абцисс соответствует времени в секундах, а ось ординат – напряжению в вольтах. На Рис. 2 видно, что УЗВ в образце с дефектом приходит к ПЭП позже, чем без дефекта. Профиль УЗВ представлен на

Рис. 3. Продольные и поперечные волны разделены: первые представлены синим цветом, а вторые — оранжевым.

На Рис. 4 представлены сигналы напряжения на выходе ПЭП преобразователя для исследуемых образцов при fo = [1,5; 2,0; 4,0; 8,0] МГц. На Рис. 4–а видно, что время прихода сигнала на ПЭП от образца с дефектом совпадает с временем от образца без дефекта. А на Рис. 4–б и Рис. 4–в видно, что время прихода сигнала на ПЭП от образца с дефектом меньше, чем время от образца без дефекта. На Рис. 4–г отсутствует сигнал от образца без дефекта. Это связано с расположением дефекта и свойствами призмы, ввиду которых не происходит обратнатная трансформация достаточно слабых УЗВ из исследуемого образца в призму. На Рис. 4 отчетливо видно затухание выходного сигнала в зависимости от fo.

На Рис. 5 представлены профили УЗВ для f 0 = 1,5 МГц.

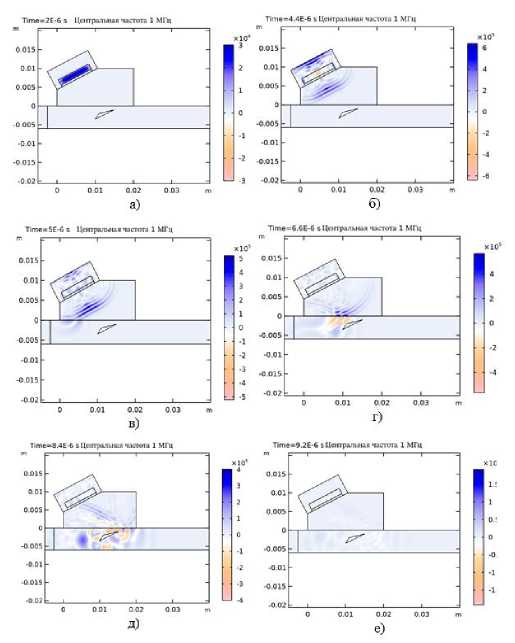
Рис. 3. Профили волн при t = 2, 4.4, 5, 6.6, 8.4 и 9.2 мкс. Центральная частота 1 МГц.

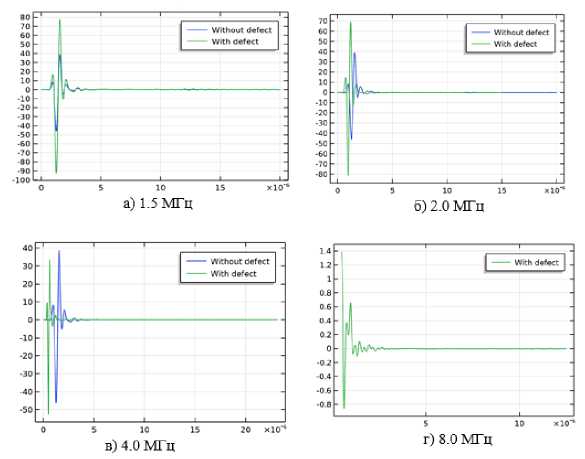
Рис. 4. Сигнал напряжения на выходе ПЭП с f ) = [1,5; 2,0; 4,0; 8,0] МГц.

Заключение

Основные выводы состоят в следующем.

• 1.    Представленные         результаты

• 2.    Зависимость от центральной частоты времени прихода сигнала, позволяет создавать методики для хорошей оценки местоположения дефекта.

• 3.    Применение разрывного метода конечных элементов Галеркина (dG-FEM) для нахождения решений волнового уравнения в задачах прикладного характера позволяет проводить качественный и ко-

• личественный анализ полученных решений с меньшими затратами вычислительных ресурсов. Это связано с возможность ограничения величины размера конечного элемента.

• 4.    Полученные результаты можно применять при решении различных задач дефектоскопии металлоконструкций ОТИ.

показывают нелинейную зависимость обнаружения дефекта в исследуемом образце от частоты напряжения подаваемого на ПЭП. Но необходимо учесть, что для разных материалов, из которых изготовлены призма и исследуемый образец, результаты будут отличаться от приведенных в работе.

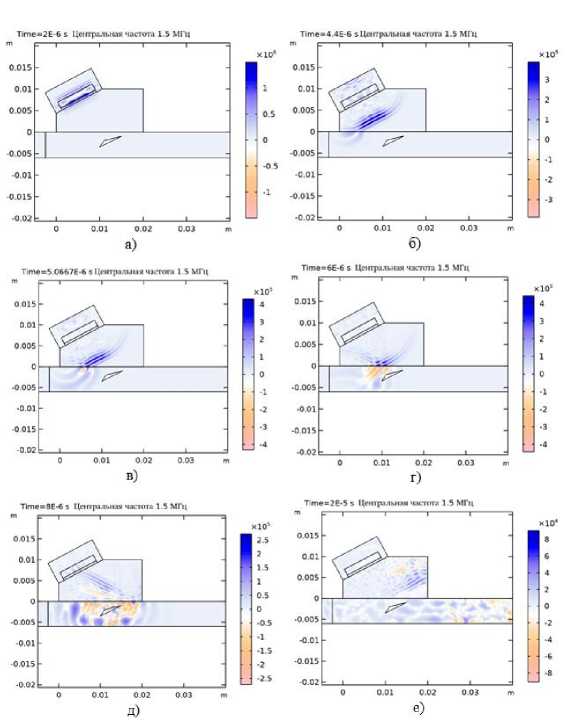
Рис. 5. Профили волн при t = 2, 4.4, 5.066, 6, 8 и 20 мкс. Центральная частота 1.5 МГц.