Determination of parameters behind an oblique shock wave on a wedge using numerical methods in the Python programming language

The goal of this study is to investigate conditionally and unconditionally converging iterative methods for solving nonlinear equations.

Problem Statement:

Determine the parameters behind an oblique shock wave on a wedge using numerical methods for solving nonlinear equations, specifically

Newton's Method (Tangent Method) and the Secant Method.

A flow of an ideal inviscid gas with an adiabatic index к = 1.4 impacts the wedge. The task is to determine the shock wave inclination angle в from equation (1):

/(0c) = sin2 вс —

^+1 sin в с sin p cos(e c -0)

- (“)2 = °'

\ mJ     ’

Where:

ft - wedge angle in radians (degrees);

0_S - shock wave inclination angle in radians (degrees);

M 1 - Mach number of the incident flow, defined by the formula;

K - adiabatic index of air.

The solution is to be found in the interval (0, π/2) using both Newton's Method and the Secant Method.     The     following     parameters

( pressure P₂, temperature T₂, density p₂, Mach numbe ) behind the shock wave are to be calculated. The results for 0 must be presented in degrees and compared in a summary table alongside the other parameters.

Table 1. Parameters of the Incident Flow (Example)
P 1 , Pa	T 1 , К	М 1		в, °	Method
98000	278	4		25	Newton
Theory The key feature of supersonic flows is that, under deceleration conditions, they form discontinuity surfaces where the flow parameters			change abruptly. These surfaces, whose positions do not change over time, are called shock waves (SW).

A shock wave formed under real-world conditions has a certain thickness comparable to the mean free path of gas molecules. The change in gas parameters within such a shock wave is not instantaneous but occurs rapidly, with continuous changes in the gas state.

The most common scenario for shock wave formation occurs when bodies are moving recti-linearly at a constant supersonic speed (Figure 1).

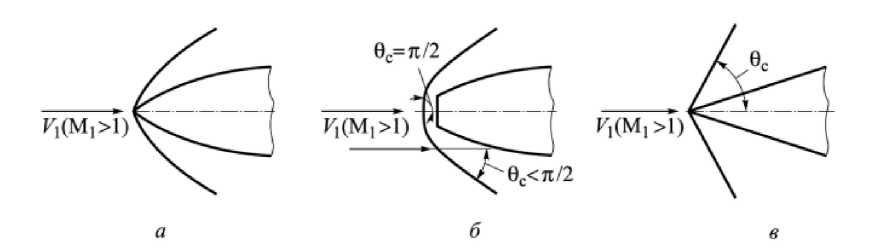
Figure 1. Types of Shock Waves

From the figure, it can be seen that shock wave surfaces can either be oriented perpendicular (Figure 1b) to the incident flow velocity vector v1v1 or inclined at some angle (Figure 1c). In the first case, the shock wave is called a normal shock wave (NSW), and in the second case – an oblique shock wave (OSW).

The ultimate goal is to determine the parameters behind the shock wave, as well as the angle of inclination of the shock on the wedge (Figure 2).

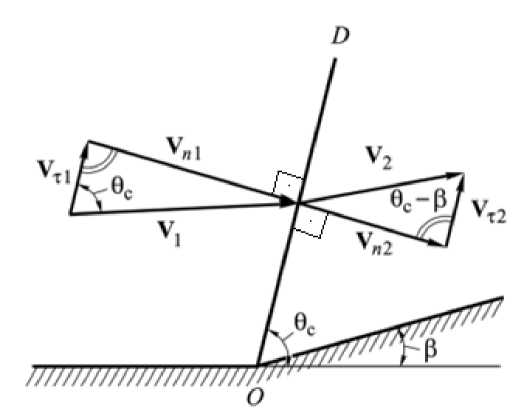
Figure 2. Diagram of Velocity Decomposition Before and After the OSW

Newton’s Method (Tangent Method)

Newton's method is based on approximating the studied function f(x)f(x) by a simpler function—in this case, a tangent. Geometrically, a tangent line is drawn at the initial point x0x0 of the curve f(x)f(x) and its intersection with the x-axis is found (Figure 3).

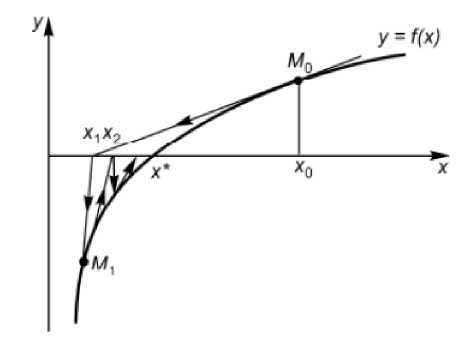
Figure 3. Newton's Method

The successive approximations can be found by drawing tangents from points M 1 , ...,M_n-1 , keeping in mind that f'(x_n) ^ 0 :

xn+1 = x1   \\хпУ(2)

Newton's method is conditionally convergent, meaning that for convergence:

lim xi = x*(3)

i^ от

The following condition must be met in the root-finding region:

|/(x)/"(x)| < (f'(x))2,(4)

Where x * is the desired root value. It is important to note that fulfilling Bolzano-Cauchy theorem conditions is not sufficient for accurate convergence. The verification of If (x)f '' (x)| < Cf'(x')')² over the entire interval is mandatory. Otherwise, convergence will only occur in the vicinity of the root.

Secant Method

Calculating the derivative f'(x), required for Newton's method, is not always convenient or feasible. Replacing the derivative with the first divided difference, found from the two most recent iterations (i.e., replacing the tangent with a secant), leads us to the Secant Method. From the perspective of analytical methods, a straight line passing through the two most recent points xn and xn-1 is used, meaning that instead of the derivative in Newton’s method, the following is substituted:

f' =

f&n ) f&n—l )

^xn ~ ^X n-1

This results in the secant method formula:

xn+1

x

n

—

^ n ^ n-1 ^fCx n )^—f(x n-1 )

fM-

The Secant Method is a two-step process, meaning it requires two initial points x₀ and x 1 . For x₀, we can take the boundary of the initial interval. This method is illustrated graphically in Figure 4.

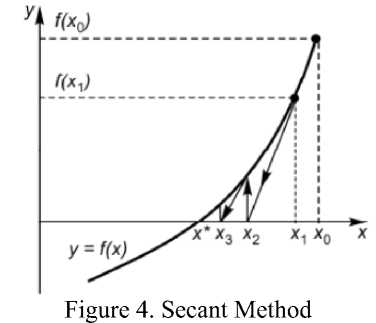
In the Secant Method, boundary values x₀ and x 1 can be taken if the Bolzano-Cauchy theorem conditions hold in the interval.

First, we draw a straight line through the selected points (x₀,f(x₀)), (x₁,f(x₁)) and determine x₂, with the vertical line at point x₂ giving f(x₂). Then, the line is drawn through points (x₁,f(x₁)) and (x₂,f(x₂)) and so on, until one of the following conditions is met: |x_n+1 — x_nl <  e or |f (x_n)| <  E 1 , signaling the end of the iterative process.

Task Execution:

The code for all tasks was implemented in Ju-pyter Lab on a local machine in Python. The following libraries are required for code execution:

Upon applying Newton's method under the given conditions, it was found that the derivative does not change sign in the interval (0, π/2), and the function does not take different signs within this interval. Therefore, the equation has no single root on this interval. We manually selected different intervals for further calculations.

Let's manually select different intervals:

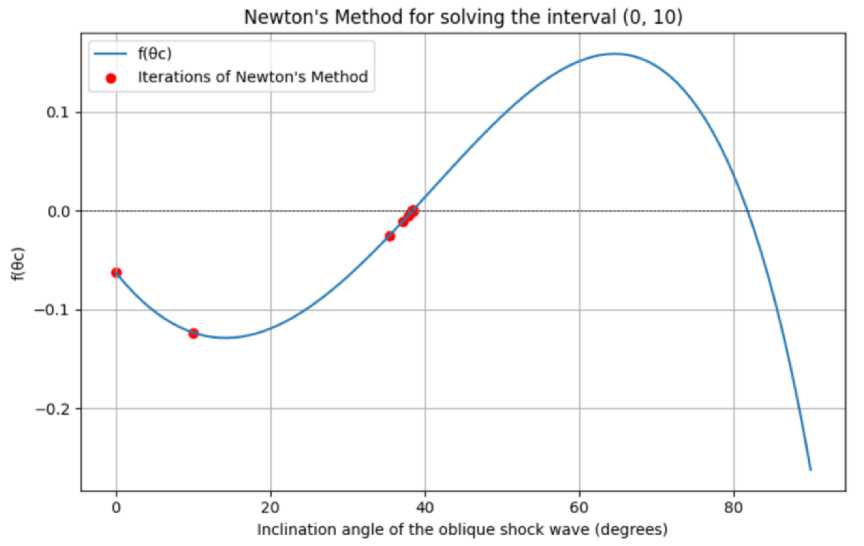
Figure 5. Graph of the function depending on the oblique shock wave inclination angle (degrees) for the interval from 0 to 10

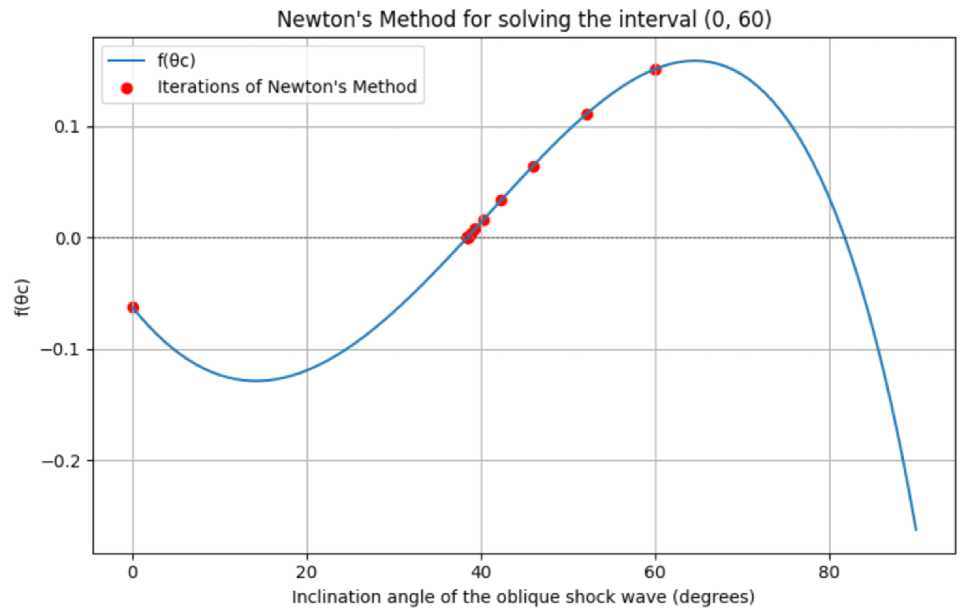
Figure 6. Graph of the function depending on the oblique shock wave inclination angle (degrees) for the interval from 10 to 60

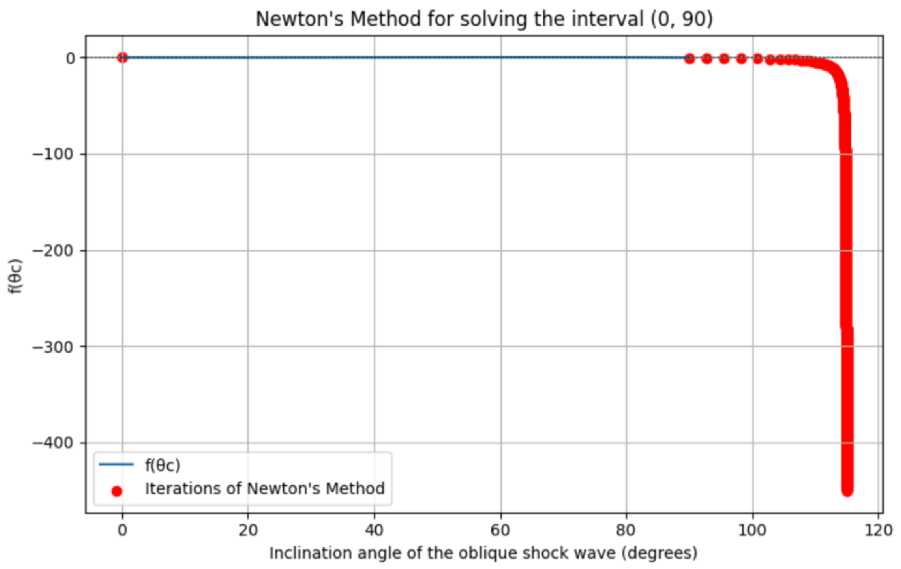
Figure 7. Graph of the function depending on the oblique shock wave inclination angle (degrees) for the interval from 0 to 90

After selecting a new interval, it was found that the function takes on different signs in the interval (π/18, π/3). It was also found that the derivative does not change sign in the interval

(π/18, π/3). Thus, we select the interval (π/18, π/3).

We call Newton's method on the new interval:

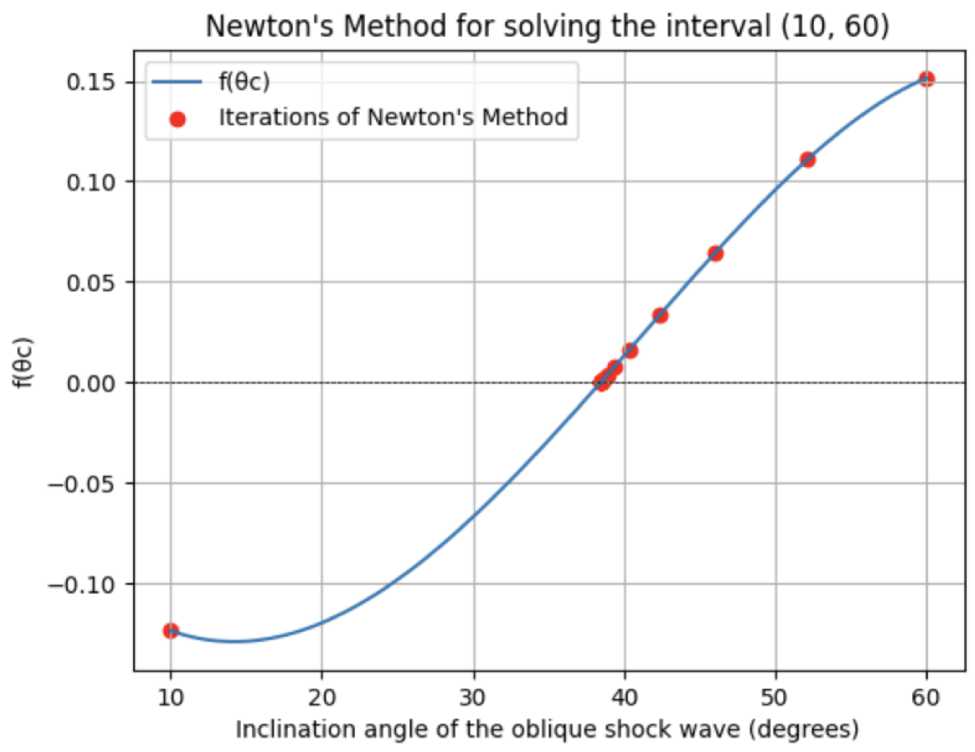
Figure 8. Graph of the function depending on the oblique shock wave inclination angle (degrees) for the interval from 10 to 60

Next, we measure the execution time of the method and calculate the given parameters.

Results:

For Newton’s method:

Iterations: 24

Execution time: 0.00186 seconds

Table 2. Results for Newton’s Method

0 , °	P 2 , Па	Тг, К	₽.5 м3	м 2
38.459	691298.770	590.878	4.081	2.209

For Secant Method:

Iterations: 4

Execution time: 0.00085 seconds

Table 3. Results for Secant Method

0 , °	Р г , Па	Т г , К	р^ м 3	М г
38.459	691298.770	590.88	4.081	2.21

Table of results for finding 0 sing different methods (Secant and Newton):

Table 4. Results for finding в using different methods

в , °	P 2 , Pa	T 2 , К	kg p2 ’m 3	М 2	Method	Time, sec	Iterations
38.459	691298.770	590.878	4.081	2.209	Newton	0.00186	24
38.459	691298.770	590.880	4.081	2.210	Secant	0.00085	4