Developing a Compact and Practical Online Quiz System

Published Online September 2014 in MECS DOI: 10.5815/ijmecs.2014.09.01

E-learnings have been widely acknowledged as useful methods to teach and learn. The authors as college teachers have been conducting many quizzes online for several courses of mathematics and statistics and computer sciences by using a web based system called QDB ( abbr. Quiz DataBase) [1][2]. Although the 1-st author is not a specialist of programming at all, he could develop this online quiz system almost by himself and modify it as he wished. This is mainly because the web browsers provide us with generic user interfaces and the web server and background programs such as relational databases and script languages provide us with a fairly sufficient power to develop what we want and most importantly they are easy to use owing to the decades of the fine efforts to improve the usability of computer software. Who could imagine twenty years ago when the web just started that an amateur can make a practical online application in a week? But this is what the 1-st author did six years ago when he developed the first form of QDB to conduct a math placement test to new students. Of course until then the author had learned by himself the script language Perl and the relational database language SQL and the web language HTML but had (has) no time or knowledge to concentrate on programming because teaching is the author's job and programming is just a tool for helping his job. The magic of the web applications comes from the fact that the main tasks are done by the web server and the browser and the database etc and what you have to do is just to paste together the tasks they do by writing short programs of pragmatic languages like Perl, Python, PHP etc. Our system stays simple mainly because it has been developed according to our practical needs which resulted in keeping the system from being unnecessarily complicated and in keeping the system easily modifiable. In this paper, we show how our system can satisfy our needs in an effective way and how simple to implement a functionality to the system thus suggest a possibility of such systems in e-learning.

The paper is organized as follows. In the rest of this introduction, we explain the structure and the functionalities of QDB thus let the reader get a basic understanding of the system. In the next section II, we review the related works which focuses math online quizzes as we do. In the section III, we show the effectiveness of QDB by analyzing the questionnaires to the students and the records of online practices and quizzes and the recently added functionality which allow the students to retry on an online quiz. In the section IV, we show the simplicity and the speed of the QDB which are the advantages to of the system. The final section V argues how easily online quiz systems can be developed.

• A.    The Structure of QDB

The structure of QDB has no secret. It is a simple web application which consists of the followings:

• •    Web browser as the user interface

• •    Apache web server to be in charge of communications between clients and the server

• •    MySQL database to store problems and quizzes and records of conducted quizzes etc.

• •   LaTex to MathML transformation program

written in Perl

• •    Maxima to evaluate (auto-scoring) student's

answers

• •    Perl scripts to make use of the players above

• •    Javascript to implement some GUI interfaces

All software we use in QDB are open source and Apache and MySQL are popular web server and relational database. Among web browsers, we usually use Firefox because we rely on MathML to display mathematical equations on screen and Firefox can render MathML and display equations quite well. MathML is a markup language for math equations recommended by W3C and provides a much needed foundation for the inclusion of mathematical expressions in web pages. There are other methods of including math equations in web pages but the reason why we chose MathML is that MathML can put html input boxes in an equation. In QDB, equations should be able to include html input boxes because most problems QDB deals with are fill-inblank questions and it should be better to have input boxes inside the equations (see Fig.1 problem 2) than to have them outside of the equations.

Maxima is an open source computer algebra system which can evaluate the validity of an equation in the form the correct answer = the student’s answer thus can evaluate student’s answers. Perl we use as our web script language can also evaluate student’s answers in a similar form (= = instead of =) but Perl doesn’t care much about the preciseness of rational numbers calculations maybe because of the floating point number system. We can use both Maxima and Perl to evaluate student’s answers. For speed, we can choose Perl and for functionalities, we can choose Maxima.

The only lines of code of the system the author had to write were those of web scripts in Perl which now are just about 2600 lines altogether. The rest are provided free and ready to use.

For running QDB, we use just one server with CPU Xeon 3.0MHz and Memory 2GB run by Linux Fedora 10 which has been proved quite enough to serve at most 120 students at a time through 100 BASE-T LAN.

Javascript is used to reorder problems and categories of problems displayed on screen (as in Fig.3) by drag and drop operations of a mouse and to display math equations in the course.

• B.    The Functionalities of QDB

What QDB can do are the followings:

• • Teachers can make problems (or questions for questionnaire) and quizzes which consist of those problems and register them.

• >    A problem to be solved online should be a fill-in-blank type if the examiner wants the student’s answer evaluated automatically.

• >    A quiz consists of problems and can be an online quiz or a printed quiz.

• >    An online quiz can be an exam or a questionnaire or an exercise.

• >    A link to an online quiz entry page can be generated and set at the site of QDB.

• >    A PDF or LaTeX source of a page of a quiz can be generated and can be used for a paper exam.

• Students can take an online exam or answer a questionnaire or do an online exercise through network.

• >    Students can do online exercises in their home on a networked PC or a Smart Phone in which a browser with MathML support is available.

• >    If students are stacked in solving a problem during an online exercise, then they can refer a hint or a related problem with an answer by a ‘hint’ buttpon or a ‘sample’ button on an exercise page.

• >    If students are asked to input an answer in the Maxima's way, then students can check their inputs ( see Fig.1 and explanations for it).

Teacher’s accesses to administration pages of QDB require a login for securities and student’s accesses to exercise pages require a login for storing student’s history to display what has been done on exercises (see Fig.1 and Fig.2).

In Fig.1 and Fig.2 and Fig.3, we show some visual images of QDB interfaces to give the reader more concrete understandings of QDB.

Fig.1 is a PC screen of an online quiz (made for a demonstration consisting of two problems) in which the examinee is checking the well-formedness of the equation in the answer box and whether the equation is what he/she intended by pushing 'Check your equation' link. If the student’s input is well-formed equation in the Maxima’s way, then the image of the equation is displayed on a small window (as in Fig.1) and if not, then QDB displays a warning.

After a student taking an online exam of QDB finishes the exam, he/she pushes the submit button (one below left in Fig.1) and he/she will immediately get his/her score. Fig.2 below is a Smart Phone screen showing all the problems in an exercise (made for a demonstration consisting of one problem) were done with a congratulation message on top.

Fig.3 is a partial view of an adminitrator’s page in which teachers can make, edit and delete problems. Each problem is shown in a line in which there are from the left, the problem id number and the title (the equation involved with the problem in Fig.3) and the update copy delete buttons and the quiz id numbers which uses the problem. The expression [maxima] in the title means that the problem is evaluated by Maxima. The problem without this expression is evaluated by Perl. The copy button is used when we want to make a similar problem. The blue characters represent links to the problem and the quizzes that it occurs. A problem which occurs in an online exam (not an exercise) cannot be deleted and so the delete button is not shown.

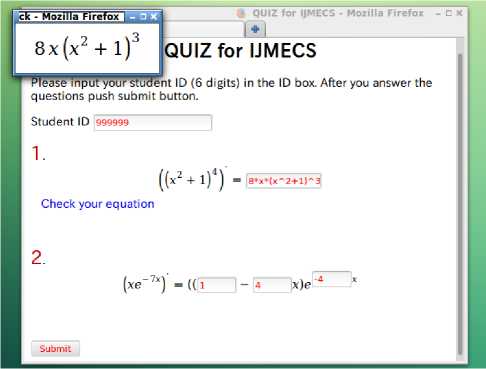
Fig.1 : A view of an online examination on PC screen

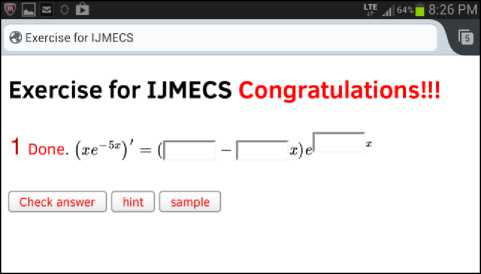
Fig. 2 : A view of an exercise on Smart Phone screen

897 p cos х - ^[maxima] 944 xe"px2[maxima]	| update 1 1 pdate	copy | copy |	208 : 220
875 xpVx[maxima]	| update 1 1	copy ||	delete | 206
622 sin ^ + езх 642 cos4 x sin x	update | | update 1 1	copy II copy |	delete | 92 2 95 11
872 -^[maxima]	| update 1 1	copy ||	delete | 212

Fig. 3 : A partial view of an administrator’s page to make and edit and delete problems practices of online quiz systems which focuses on math quizzes as we do.

Anderson [3] suggests teachers in STEM (Science, Technology, Engineering and Mathematics) fields to use the right tools for e-learning which include math equation editors and real time communication tools. She showed fine examples of students' comunications with their presentations of math equations using these tools. The paper suggests the possibilities of math communications (if not real time) online that could help students do online exercises with assistance from teachers and other students.

Major LMSs (Learning Management Systems) like BlackBoard, WebCT, and Moodle have online quiz functionalities. Moodle [5] is an open source LMS which is a web application written in PHP and backed by MySQL or PostgreSQL. Moodle has online quiz functionalities in which quizzes are classified into Moodle qtypes. Among those qtypes we would like to focus on Stack 3.0 [6], an open source math quiz system, because of its innovativeness for math tests. Stack can be used by adding it to Moodle as a Moodle qtype module. Stack uses the computer algebra system Maxima to evaluate complex mathematical equations in student's answers. QDB had used Perl to evaluate student's answers on online quizzes. But because our policy of developing QDB is to exploit the strong power of open technologies, QDB followed Stack to utilize Maxima's versatile applicability to math equations for auto-scoring student's answers. But still QDB uses Perl for evaluating simpler answers for speed. Stack also inspires us by its ability to evaluate partially correct answers which QDB still lacks. In Stack a teacher can give a partial score to a partially correct answer by using the so-called potential response tree. The potential response tree is a quite elaborate mechanism which people might find difficult to understand. But partial scoring is definitely a necessary function for evaluations of relatively complex problems with many points to be evaluated. For students to write mathematical equations, Stack adopted Maxima's way of writing equations. For example, see Fig.1, or Maxima writes the equation (1)

xsinx

II. Related Works

1 + x2

There are many online quiz systems around. We review here recent activities of developments and as the character string:

(sqrt(x)*sin(x)) / (1+x^2).

The Maxima's way of writing equations is fairly common among computer languages and applications. But it is not an easy task for students without experiences of this kind of type settings to input their answers in the Maxima's way. QDB uses the Maxima's way of writing equations only for experimental purposes because a main purpose of QDB is conducting examinations which affect the grades of students and we think that our students are not accustomed to write equations in the Maxima's way. Thus compared to QDB, Stack is of a research oriented nature and aims at higher ideals for math online quizzes. QDB has been developed so that it satisfies daily needs of our classes and so of a quite practical nature. But both uses today's open technologies to realize their needs or ideas.

As we came to use Maxima in QDB, the use of Open Source applications on the high level like Maxima, Octave, Scilab, R, etc have gained considerable attention in science and engineering education in different fields of various disciplines across the globe [8]. In the future, more and more intelligent functionalities will be expected in e-learning systems and we acknowledge the importance of open source technologies in higher level math related applications therewith.

• III.    Effectiveness of QDB

The effectiveness of QDB will be shown on the basis of practical uses in the authors' classes. We have conducted more than a hundred online quizzes in classrooms for 6 years using QDB and had no accidents which delayed the exams or caused the results of exams invalid.

• A.    Student Questionnares and Quiz records

The authors conducted two questionnaires on online quizzes of QDB in Calculus classes [1][2]. We summarize here how students respond to the two questionnaires (we cite them as 1st and 2nd) in Table 1. 216 students answered the 1st and 212 students the 2nd. The questions ask how good the QDB is for the point concerned. The highest evaluation answer is assigned the score 5 and the lowest 1. While the questions were asked in Japanese, we translate them into English in Table 1.

Table 1. Summary of the two questionnaires on QDB

Question	Avg .
Q1. Didn't you have any difficulties to choose Firefox as the browser during the online exams in classrooms?	3.71
Q2*. Didn't you have any difficulties to input your answers into the answer boxes during the online exams in classrooms?	3.61
Q3. Didn't you have any difficulties in process between the quiz submission and the score check?	3.83
Q4. How good is it to get your score of an online exam immediately after you submit your answers?	4.53
Q5*. Did the online exams motivate your learning?	3.89
Q6**. How good is it to collate your online exam answer with the correct answer after the exam?	4.39
Q7**. How good is it to see the congratulation message when you finish an online exercise?	4.14
Q8**. Did hints and samples help you?	4.00

* indicates the question is in the 1st questionnaire.

** indicates the common questions of the two questionnaires for which the Avg. shows the total average of the two questionnaires.

Non-marked questions are only in the 2nd questionnaire.

The most popular functionality of QDB is the instant scoring of the exams (Q4) which helps teachers a lot too and seems the most successful functionality of online tests in general. Relatively high average scores of the questions Q6,7,8 are the results of the improvements which correspond to the feedbacks from students and our experiences.

The questions Q1,2 show the negative aspects of the system. As many researchers of e-learning admit ([7][9] for example), computer literacy is the key for the success of online systems and human communications help the systems working a lot which in fact we found in our experiences in QDB. This implies the needs of more intelligent supports of the system when no human supporters exist since autonomous learning of students is important ([10] shows the importance of such autonomous learning in Engineering, for example) .

For online exercises we compared the improvements of the scores of the quizzes from the scores of the placement test between the Calculus students who used the online exercises more than 40 times and the students which did not use the online exercises. The number of uses of the online exercises are counted by the login records of the online exercises. The scores of the quizzes are represented by the average of the two quizzes. Fig. 4 shows the differences between the two groups. We can see that the regression lines distinguish the two groups.

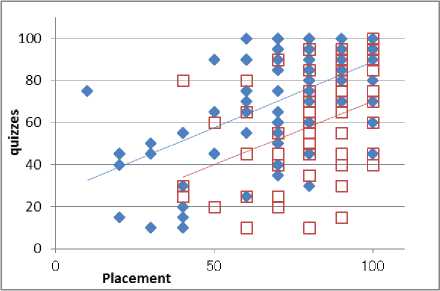
Fig 4. The relationships between the scores of quizzes and the scores of the placement for the two groups

Blue are the group with more than 40 times usage of the online exercises. Red are the group with no usage of the online exercises.

The averages of the differences of the scores of the quizzes from the scores of the placement are calculated for the two groups: 0.51 for the group using the online exercises more than 40 times and -22.5 for the group not using the online exercises. If we regard the two groups as statistical samples from populations, then we can test the significance of the difference of the two averages by Welch's t-test which results in that the P value is just 2.86E-9.

• B.    Effects of Retry on Online exams

When a teacher registers an online exam in QDB, he has an option to make the exam to be retried (namaly, a student can correct the wrong answers after he/she submits the exam). Of course, the instant evaluation functionality specific to an online exam make this retry functionality possible. We show by a case study the effectiveness of the combination of these two online merits.

In Linear Algebra class 2013, the first author conducted three quizzes during the semester in each of which he allowed the students to retry. We set QDB so that students are allowed to retry just once. Table 2 shows the results. Each line in the table represents the scores of a student in the class and a blank cell means he/she did not take (or retry) the quiz.

Table 2. Results of Retry in Quizzes

Quiz1		Quiz 2		Quiz 3
1st	Retry	1st	Retry	1st	Retry
71.4	85.7	100		40	40
100.0		25	25	80	100
100.0		100
71.4		100		20	60
		0		60	100
71.4	85.7	25	25	80	100
100.0		0		80	100
85.7	100.0	100		100
71.4	85.7	75	75	80	100
71.4	100.0	25	25	80
57.1	71.4	0	0	80	80
100.0		100		100
28.6	57.1	0		80	100
100.0		100		80	100
100.0		100		100
100.0		75	75	60	80
100.0		75	75	100
28.6	28.6	75	100	100
100.0		25		60
85.7	100.0	25		100	100
85.7	100.0	100		100
85.7	100.0	75	100	80	100
100.0	100.0	75	75	100	100
		75	100	60	100
100.0		50		80	100
28.6	57.1	25	50	100
71.4	100.0	0	25	40	40
80.6	89.7	56.5	61.1	78.5	90.0

The figures are the percentages of correct answers.

1st means the first attempt. The bottom row shows the averages of the class (the averages of Retry mean the averages of the class after Retry).

Significant improvements of the scores can be observed by comparing the class averages of the 1st attempts and the class averages after the retries. Retry not only improves students' scores but also compensates for the lack of partial scoring functionality in QDB by providing students with chances to correct a few errors in multiple answer boxes in a problem (if they can't correct, the score for the problem is zero) etc.

• IV.    Simplicity And Speed Of QDB

  As we said before, the maintainable part of QDB is just 2600 lines of Perl code. Accordingly the amount of the work needed to add a functionality is not huge. As a case, we show how easy it was to add the retry functionality described in the last section. We added a table quiz_result_2 to the MySQL database for QDB to store the retry results. The structure of quiz_result_2 is just identical to that of the table quiz_result to store the 1st attempts. Then, we added the retry option in registering a quiz and let students notice the possibility of a retry when they submit their 1st attempt and the modification of showing the results of the quiz (for teachers) was just to distinguish to add the contents of the quiz_result_2 table or not. That's all. The details of these tasks described above were not lengthy at all because programs like the web server and the relational database and Maxima etc do the almost all essential jobs instead of us. All the tasks above took less than 50 lines of Perl code added and less than a week to add those lines.

Our measurement shows that QDB is fast (Table 3). The measurements were done with a single client (Core i5 3.33GHz) and a server (Xeon 3.10GHz) using app.telemetry addon of Firefox on the client.

Table 3. Responses of QDB

Action	Avg	Stdev
(1) Registration of a problem	559	42.9
(2) Display of a quiz	153	19.1
(3) Check of an equation	276	15.2
(4) Submit quiz and get the score	393	34.3

Avg is the average response. Stdev is the standard deviation. The figures are milliseconds.

Every action ends in a second and our experiences showed all the actions but (2) end alike in a class room maybe because the actions (1)(3)(4) do not concentrate in a short time period. For (2), in a classroom where more than 50 students use QDB, displaying a quiz on each screen of the students sometimes take a few seconds or more at the beginning of an exam but has never been disturbing for the exams. If there are more than ten problems in an exam and all the problems use Maxima to evaluate students' answers and more than fifty students take the exam, then it usually take about thirty seconds to evaluate the exam which is fairly a long time to wait but we don't evaluate exams so often.

• V.    Conclusion: How System Can Be Developed

Acknowledgment

The authors wish to thank our students who took our online exams and gave us useful feedbacks through their e-learning and questionnaires without which our work could not be done.