Диагностика насыщения внутренних атмосферных волн и определение их характеристик в стратосфере земли с помощью радиозондовых измерений

Фундаментальной задачей физики атмосфер планет является исследование волновых процессов, которые, как показывают результаты наблюдений, определяют атмосферную динамику на всех высотах [Губенко и др., 2012] . Важная роль внутренних гравитационных волн (ВГВ), в первую очередь, связана с тем, что они обеспечивают эффективный механизм переноса энергии и импульса из нижних слоев атмосферы в верхние. Большой интерес к ВГВ со стороны специалистов по ионосфере связан с тем, что многие ионосферные процессы и процессы распространения радиоволн хорошо объясняются путем привлечения понятий атмосферных волн. Согласно интерпретации, принятой в настоящее время, перемещающиеся ионосферные возмущения и спорадические слои E s представляют собой ионосферное проявление волн в преимущественно нейтральной атмосфере [Госсард, Хук, 1978; Gubenko et al., 2018] . Источниками генерации ВГВ в атмосфере могут быть тепловые контрасты вблизи поверхности, топография, сдвиговая неустойчивость ветра, конвекция и фронтальные процессы. В атмосфере Земли в отсутствие диссипации энергии амплитуда волновых возмущений скорости ветра или температуры растет примерно экспоненциально с увеличением высоты и поэтому возмущения с малой амплитудой вблизи поверхности могут производить значительные эффекты на больших высотах, где происходит обрушение волн и передача энергии и импульса ВГВ в невозмущенный поток. Поскольку ВГВ являются характерной особенностью устойчиво стратифицированной атмосферы, аналогичные эффекты можно ожидать в атмосферах Венеры и Марса. Полагают, что на Марсе внутренние атмосферные волны могут играть более важную роль, чем на Земле, так как во многих случаях амплитуды ВГВ в атмосфере Марса оказываются существенно больше своих земных аналогов [Creasey et al., 2006; Gubenko et al., 2008a; Губенко и др., 2012, 2015, 2016a] .

Зондирование внутренних волн любыми способами сталкивается с проблемой, суть которой в том, что измеряемыми являются параметры возмущенного состояния атмосферы, например скорость ветра, температура или плотность, и по этому измерению необходимо определить, какая часть сигнала обусловлена ВГВ. Общий подход здесь заключается в том, чтобы отделить мелкомасштабные вариации от медленных изменений невозмущенного состояния и считать эти вариации связанными с волновыми проявлениями. Так, если измерения представляют собой временные реализации для фиксированного места наблюдений, например, как в случае измерений, выполняемых с помощью лидаров или радаров, указанное выше разделение масштабов можно осуществить в результате частотного анализа. Однако при этом необходимо учитывать, что не все анализируемые мелкомасштабные вариации обусловлены ВГВ. Наблюдаемые вариации могут быть связаны не только с внутренними волнами, но также с влиянием регулярных тонких слоев или турбулентности в атмосфере планеты. Корректная интерпретация результатов исследования ВГВ предполагает наличие дискриминационного критерия идентификации волновых событий. Только в том случае, когда данный критерий удовлетворяется, анализируемые вариации могут рассматриваться как волновые проявления в атмосфере планеты [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015, 2016a, b, c].

Спутниковые наблюдения в атмосфере радио-затменным методом являются мощным средством радиофизических исследований активности ВГВ по всей планете с почти однородным и высоким качеством экспериментальных данных [Gorbunov, Gurvich, 1998] . Анализ вертикальных профилей вариаций температуры, определяемых из радиозатменных экспериментов, дал возможность найти некоторые статистические характеристики (потенциальную энергию ВГВ на единицу массы) внутренних волн в атмосфере Земли [Steiner, Kirchengast, 2000; Tsuda et al., 2000; Tsuda, Hocke, 2002] . Преимуществом радиоза-тменных измерений с целью изучения внутренних атмосферных волн является широкий географический и временной охват исследуемых районов, позволяющий проводить глобальный мониторинг волновой активности в атмосфере планеты [Gavrilov et al., 2004; Гаврилов, Мануйлова, 2016] . Этот метод дает возможность получать в глобальном масштабе вертикальные профили атмосферных параметров (давления, плотности и температуры) с высоким вертикальным разрешением при любых погодных условиях [Liou et al., 2003, 2004; Pavelyev et al., 2009, 2012, 2015] . Однако до недавнего времени исследователи полагали, что восстанавливаемых вертикальных профилей температуры и плотности в радиозатменных экспериментах недостаточно для количественного описания волновых эффектов в атмосфере планеты [Губенко и др., 2012, 2015] .

В этой связи мы разработали оригинальный метод идентификации дискретных волновых событий и реконструкции параметров ВГВ по результатам анализа индивидуальных вертикальных профилей температуры, плотности или квадрата частоты Брента— Вяйсяля в атмосфере планеты [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015]. Метод не требует какой-либо дополнительной информации, не содержащейся в профиле, и может быть использован для анализа вертикальных профилей, полученных любыми способами. Сформулирован и обоснован пороговый критерий идентификации волновых событий, при выполнении которого анализируемые вариации могут рассматриваться как волновые проявления [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015, 2016b]. Метод базируется на анализе относительной волновой амплитуды, а также на положении линейной теории ВГВ, согласно которому волновая амплитуда ограничена пороговой величиной динамической (сдвиговой) неустойчивости в атмосфере. Предполагается, что, когда амплитуда внутренней волны достигает порога сдвиговой неустойчивости по мере распространения волны вверх, диссипация волновой энергии происходит таким образом, что амплитуда ВГВ поддерживается на уровне указанного порога (насыщение волновой амплитуды). Для апробации и проверки разработанного метода мы использовали данные одновременных зондовых измерений температуры и скорости ветра в стратосфере Земли [Cot, Barat, 1986]. С помощью анализа годографа скорости ветра авторы этой работы идентифицировали насыщенную ВГВ и определили ее характеристики. Использование зондовых измерений температуры и разработанного нами метода позволило независимым способом реконструировать все характеристики идентифицированной внутренней волны с погрешностями, не превышающими 30 % [Gubenko et al., 2008b; Губенко и др., 2012]. Применение метода к анализу радиозат-менных данных о температуре позволило нам впервые идентифицировать волновые события в атмосферах Земли и Марса, определить ключевые характеристики обнаруженных волн, включая собственную частоту ВГВ, вертикальные потоки волновой энергии и импульса [Gubenko et al., 2008b, 2011; Губенко и др., 2015, 2016a, b, c]. Результаты мониторинга волновой активности могут быть полезными при построении численных моделей циркуляции атмосферы, включающих параметризацию волновых эффектов. Экспериментальное определение и анализ географических и сезонных распределений характеристик внутренних волн [Губенко и др., 2012, 2015, 2016b] являются необходимыми и важными этапами при построении адекватных моделей общей циркуляции атмосферы Земли. Разработанный нами оригинальный метод идентификации волновых событий и реконструкции характеристик ВГВ в атмосферах планет [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015, 2016a, b, c] получил широкое признание научного сообщества как в России, так и за рубежом и в настоящее время успешно применяется при исследовании волновых процессов в атмосфере Земли [Horinouchi, Tsuda, 2009; Xiao, Hu, 2010; Rechou et al., 2014; Sacha et al., 2014; Noersomadi, Tsuda, 2017; Zagar et al., 2017] и Венеры [Altieri et al., 2014; Peralta et al., 2015]. В частности, исследователи из Франции и Швеции в своей работе [Rechou et al., 2014] показали, что данные численного моделирования и анализ независимых радарных и зондовых измерений в атмосфере Земли демонстрируют высокую эффективность разработанного нами метода и хорошую надежность получаемых на его основе научных результатов.

Радиозатменные исследования внутренних волн в средней атмосфере Земли [Gubenko et al. 2008b, 2011; Губенко и др., 2012, 2016b] используют данные одной системы наблюдения. Обычно это обеспечивает информацию только об одной независимой переменной (температуре или плотности) и обусловливает некоторую неоднозначность описания волнового поля. Когда две инструментальные системы измерений используются вместе, можно добиться значительно более полного определения характеристик волнового поля и атмосферных эффектов ВГВ. Одновременные данные о скорости ветра и температуре, полученные в ходе проведения радио- зондовых измерений, позволяют больше внимания уделить роли, которую играют внутренние волны в атмосферной динамике. В некоторых отношениях зондовые данные обеспечивают проверку радиозат-менных волновых исследований, которые используют анализ обусловленных внутренними волнами вариаций температуры или плотности в предположении насыщения амплитуды волнового поля (разработанный нами SWA-метод (saturated wave assumption)). Измеряя одновременно возмущения температуры и скорости ветра и анализируя их, можно оценить степень насыщения ВГВ без каких-либо предположений, проверить обоснованность и корректность предположения о насыщении внутренних волн и, следовательно, определить эффективность разработанного SWA-метода. Знание реальных и пороговых волновых амплитуд необходимо при оценке воздействия внутренних волн на невозмущенную атмосферу. Поскольку предположение о насыщении амплитуды внутренних волн играет ключевую роль при радиофизическом мониторинге ВГВ в атмосферах планет [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015, 2016a, b, c], радиозондо-вые исследования процессов насыщения в атмосфере Земли являются актуальными и важными. Для ради-озондовых исследований ВГВ будет применен классический метод анализа годографа скорости ветра. Предлагаемый в данной работе усовершенствованный метод годографа основан на комбинированном анализе одновременных измерений скорости ветра и температуры, в котором используется поляризационное соотношение между волновыми вариациями скорости и температуры с целью достижения минимальных погрешностей в результатах реконструкции характеристик внутренних атмосферных волн.

ТЕОРЕТИЧЕСКИЕ СООТНОШЕНИЯ И МЕТОД ГОДОГРАФА

Дисперсионное уравнение связывает собственную частоту волны ω (частота, определяемая в системе отсчета, которая движется со скоростью невозмущенного ветра) с пространственными характеристиками ВГВ (горизонтальным k h и вертикальным m волновыми числами) и с параметром стабильности невозмущенной атмосферной стратификации N b (частота плавучести, или Брента — Вяйсяля). Если для внутренних волн выполняются условия гидростатического режима: N _b ² 2 ω²> f ², m ² 2 k _h ² и m 2 ^ (2 H) ^-2, дисперсионное уравнение имеет вид [Fritts, Alexander, 2003; Gubenko et al., 2008b, 2011; Губенко и др., 2012] :

( c - u ) 2

ю² _ N 2    1

k h = m ² 1 - f ² / ю²,

где (c - u) — собственная горизонтальная фазовая скорость волны, с — горизонтальная фазовая скорость в системе отсчета земного наблюдателя (не- подвижная система отсчета), u — проекция невозмущенной скорости ветра на направление вектора kh и H.7 км — приведенная высота средней атмосферы Земли. Инерционная частота (параметр Кориолиса) f определяется выражением f=2Ω sinφ, где Ω=7.292·10–5 рад/с — угловая скорость вращения Земли и φ — географическая широта. Вектор (kh, m) определяет направление распространения фазы волны. Для внутренних волн, энергия которых переносится вверх (составляющая групповой скорости направлена вверх), фаза распространяется вниз (m<0) и наоборот. Собственная частота считается положительно определяемой величиной (ω>0).

Если ось системы координат выбрана в направлении горизонтальной составляющей k h волнового вектора, поляризационные соотношения приобретают простой вид [Zink, Vincent, 2001; Gubenko et al., 2008b, 2011; Губенко и др., 2012] :

v * = - if и', (2) ω w ' = - kh- и',                                         (3)

m

T ‘

и' = i——,         ,

N ь 4 1 - f 2/ to²

где u′ и v′ — комплексные возмущения компонент скорости ветра, направленных параллельно и перпендикулярно горизонтальной составляющей волнового вектора соответственно; w′ — комплексное возмущение скорости ветра в вертикальном направлении; T' = T' / Tb — нормированное комплексное возмущение абсолютной температуры (T=t+273°); i — мнимая единица. Комплексное и реальное физические возмущения связаны между собой простыми соотношениями. Так, комплексному возмущению u′ соответствует реальное возмущение Re u′, а его амплитуда равна модулю |u′| комплексного возмущения [Gubenko et al., 2008b; Губенко и др., 2012]. Из уравнения (2) следует, что разность фаз между возмущениями скорости и' и v' равна 90°, а отношение амплитуд |v'|/|и'| равно f/го. Поскольку годограф горизонтальной скорости ветра описывает эллипс и движение происходит в плоскости, перпендикулярной волновому вектору [Гилл, 1986], ВГВ на низких частотах при го~f является эллиптически поляризованной поперечной волной. На более высоких частотах, когда справедливо неравенство f/го^1, эл- липс вырождается в прямую линию и внутренние волны становятся линейно поляризованными. Отметим, что поляризационное соотношение (4) выполняется для внутренних волн, энергия которых переносится вверх (m<0), в противном случае (m>0) необходимо в правой части уравнения (4) поменять знак плюс на минус [Pfister et al., 1993]. Дисперсионное уравнение (1) и поляризационные соотношения (2)–(4) являются приближениями, которым соответствуют два интервала гидростатического волнового режима. Интервал промежуточных собственных частот определяется как область частот го, для которых N2 2 го2 2 f2. Здесь дисперсионное уравнение (1) сильно упрощается и дает простую связь собственной горизонтальной фазовой скорости (c - и) с вертикальным волновым числом m и частотой Брента — Вяйсяля:

|c-и| = го/|kh| = Nb /|m| [Fritts, Alexander, 2003; Гу- бенко и др., 2012]. Интервал низких собственных частот определяется как область частот, для которых го2 имеет тот же порядок, что и f2, но го2>f2.

Для вычисления частоты плавучести Nb по данным измерений вертикального профиля темпе- ратуры Tb(z) мы использовали следующее выраже- ние [Gubenko et al., 2008b, 2011; Губенко и др.,

2012] :

N2 = g f^ + g 1

b T   dz   c b V p /

где g — ускорение свободного падения, g/cp=9.8·10–3 K/м — адиабатический градиент температуры, Tb — невозмущенная (средняя) абсолют- ная температура, z — локальная вертикальная коор- дината.

Идея анализа годографа состоит в отслеживании движения (вращения) вектора возмущений скорости ветра с высотой [Hines, 1988]. Согласно теории, волновой годограф (траектория, которую описывает конец вектора возмущений скорости) имеет форму эллипса, большая ось которого параллельна направ- лению горизонтального распространения волны, а длины большой и малой полуосей эллипса представляют амплитуды возмущений скорости ветра вдоль вектора kh и в поперечном направлении соответственно. Собственная частота волны ω может быть определена из выражения для аксиального отношения AXR, в котором учтено влияние вертикального сдвига поперечной компоненты средней скорости VT ветра [Hines, 1988]:

v 1

AXR =   =

I и 1

f 1 dV _T — ω N _b dz

где | u ′| и | v ′| — длины большой и малой полуосей эллипса соответственно. Таким образом, определяя из эксперимента величины N _b, f /ω, ω и | m |=2π/λ_z (λ z — вертикальная длина волны) и учитывая дисперсионное уравнение (1), можно найти значение | k h |, горизонтальную длину волны λ h =2π/| k h | и собственную горизонтальную фазовую скорость | c - и |. Амплитуда вертикальных возмущений скорости | w ′| определяется из поляризационного соотношения (3).

Для исследования процессов насыщения ВГВ на основе найденного отношения f /ω мы вычислили относительную пороговую амплитуду a сдвиговой неустойчивости [Fritts, 1989] :

| и ; _at|      241 - f ²/ го²

I ^{c - и}\ 1 + V 1 - f ²/ го²

где |u′sat| — амплитуда насыщения горизонтальных возмущений скорости ветра, направленных парал- лельно вектору kh. По результатам анализа конкретного сеанса радиозондовых измерений мы имеем две независимые оценки относительной волновой

амплитуды a _e и a _u [Gubenko et al., 2011] :

a

e

±L J* H,2S H I c - 1 N 2^{1 1} X z N 2 I

a

u

I ¹ 1 | c - й|

hi m 1 1 - ft

N b       ω²

Величина a e вычисляется на основе анализа только температурных данных, в то время как при определении a u используются измерения как скорости, так и температуры. Степень насыщения ВГВ определяется нами как отношение амплитуды возмущений скорости | u ′| к величине волновой амплитуды насыщения | u ′ sat |, и ее можно найти из выражений (8) двумя разными способами [Gubenko et al., 2011] :

a de    «11at| a ’ d = ^1 = 0u du 1't| a

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ И ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Для демонстрации возможностей изложенного метода рассмотрим пример его практического применения к анализу одновременных баллонных измерений температуры и скорости ветра в атмосфере Земли. Данные указанных измерений находятся в свободном доступе на сайте Центра данных SPARC []. Регистрация измерений проводилась с интервалами 6 с, что соответствует вертикальному разрешению данных ~30 м при средней скорости подъема аэростата ~5 м/с. Точность измерений температуры и скорости ветра составляют ~0.2 K и ~1 м/с соответственно.

На рис. 1 представлены два профиля температуры, полученные по измерениям в атмосфере Земли над пустынным районом Desert Rock, которые проводились с интервалом ~12 ч. Высотная корреляция ква-зипериодических вариаций температуры для указанных профилей в выделенном интервале предполагает, что эти вариации могут быть обусловлены ВГВ или полусуточным тепловым приливом с периодом ~12 ч в системе отсчета земного наблюдателя. Для проверки данного предположения мы провели совместный анализ данных о температуре (рис. 1, слева), зональной и меридиональной скорости ветра (рис. 1, справа) для сеанса измерений 06.11.2008. Зональным принято направление с запада на восток, меридиональным — с юга на север.

На рис. 2 показаны анализируемые профили для выделенного нами интервала 22.5–30 км волновых проявлений. Пунктиром показаны соответствующие средние (невозмущенные) профили, вычисленные на основе аппроксимации исходных данных полиномом 3-й степени методом наименьших квадратов (МНК). Применив выражение (5) к среднему про-

филю температуры, мы получили оценку частоты Брента — Вяйсяля N b (параметр стабильности атмосферной стратификации) для анализируемого интервала N b . 2.18·10^–2 рад/с.

На рис. 3 показаны высотные профили вариаций температуры и составляющих скорости, которые определялись как разность исходных и соответствующих средних профилей на рис. 2. По ним мы определили амплитуду вариаций температуры | T ′| . 2.74 K и вертикальную длину волны λ z . 3.4 км возмущений скорости и температуры. Также был выбран интервал для построения годографа и определено значение T b средней температуры T b . 218 K в центре указанного интервала на высоте 26 км.

На рис. 4 представлен годограф горизонтальных вариаций скорости ветра для интервала высот 24.3– 27.8 км. Абсцисса и ордината показывают значения зональной и меридиональной компонент соответственно. Здесь точки — оригинальные данные, ® — начальная точка годографа, числа вблизи экспериментальных точек указывают высоту в километрах. Стрелкой показано направление средней скорости ветра V _b на высоте 26 км. Там же гладкой сплошной линией показан эллипс МНК-аппроксимации анализируемых данных, длины большой и малой полуосей которого определяют амплитуды | u ′| и | v ′| горизонтальных возмущений скорости: | u ′| . 5.63 м/с и | v ′| . 2.98 м/с. Согласно теории ВГВ, вращение конца вектора вариаций скорости по часовой стрелке с увеличением высоты в Северном полушарии соответствует распространению фазы вниз и переносу волновой энергии вверх.

Мы вычислили значение параметра Кориолиса f . 0.86·10^–4 рад/с в пункте наблюдений и, используя (6), нашли отношение f /ω и собственную частоту ω: f /ω . 0.53 и ω . 1.63·10^–4 рад/с (собственный период волны равен T ⁱⁿ=2π/ω . 10.7 ч). Далее с помощью уравнения (1) была определена величина собственной горизонтальной фазовой скорости | с - и | . 13.9 м/с и вычислена горизонтальная длина волны X h = c - й\Т ^1П . 535 км. Учитывая соотношение (3), была найдена амплитуда вертикальных возмущений скорости ветра | w ′| . 3.6·10^–2 м/с. Используя известное соотношение между собственной частотой ω и частотой волны σ в системе отсчета земного наблюдателя σ=ω+ k h V b , мы определили частоту σ. Зная направление большой оси эллипса годографа, можно найти направление горизонтального волнового вектора k h с неопределенностью 180°. Угол между векторами k _h и V b (рис. 4) близок к прямому углу (92.2° или 87.8°), поэтому k h V b . 0 и σ . ω . 1.63·10^–4 рад/с. Период волны в неподвижной системе отсчета T ^ob=2π/σ . 10.7 ч совпадает с собственным периодом T ⁱⁿ, его значение близко к обсуждаемой ранее величине ~12 ч. Это подтверждает гипотезу, что наблюдаемые квазипериоди-ческие вариации (рис. 1) обусловлены ВГВ, а не полусуточным тепловым приливом.

у 20

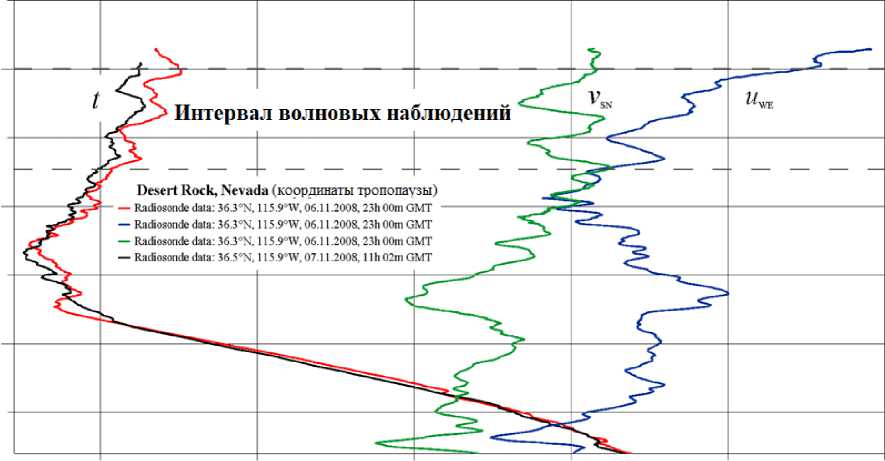
Интервал волновых наблюдений

Desert Rock, Nevada (координаты тропопаузы) — Radiosonde data: 363^ 115.9*W, 06.11.2008» 23h 00m GMT — Radiosonde data: 363°N, J15.9°W, 0611.2008,23h00m GMT — Radiosonde data: 36.3°N, 115.9 W, 0611.2008,23h 00m GMT — Radiosonde data: 36.5*N, 115.Ф1¥, 0711.2008,1 lh02m GMT

-60                -40                -20                 0                 20                 40

Температура (/), °C Скорость ветра (и^р:,г^), м/с

Рис. 1. Вертикальные профили температуры t , зональной u _WE и меридиональной v _SN скорости ветра, найденные из радиозондовых измерений в атмосфере над пустынным районом Desert Rock, Nevada

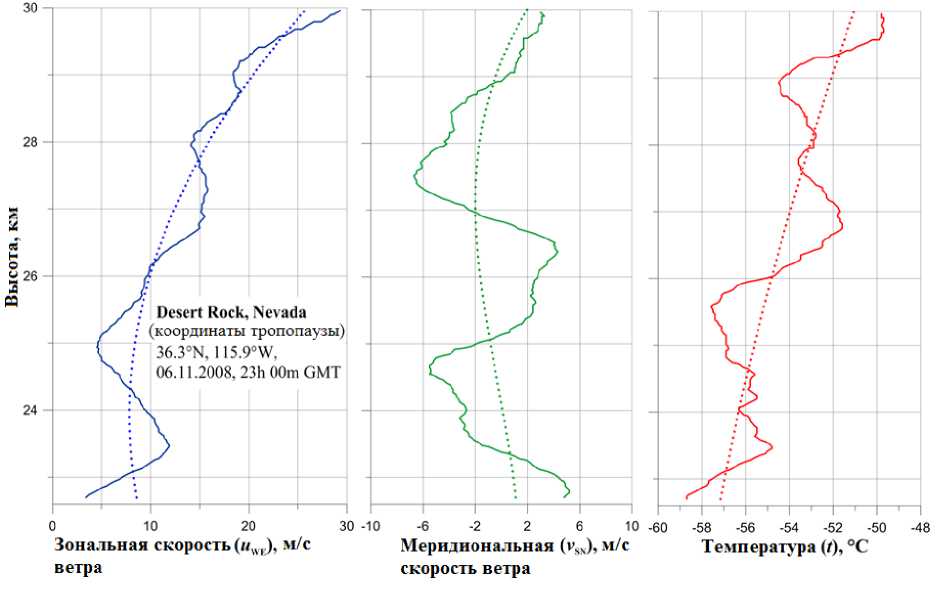
Рис. 2. Высотные профили температуры, зональной и меридиональной компонент скорости ветра, полученные из зондовых измерений 06.11.2008 в атмосфере над районом Desert Rock

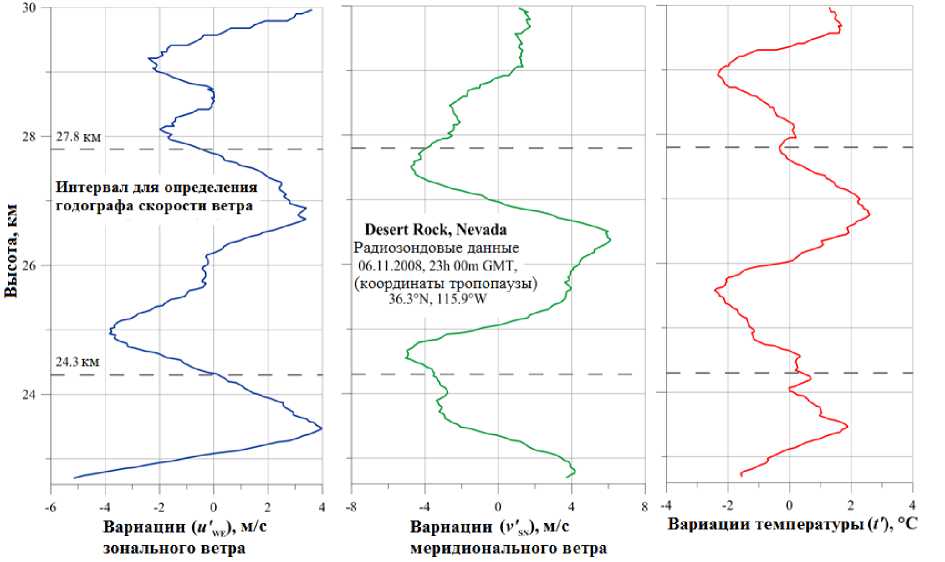
Рис. 3. Высотные профили вариаций температуры и составляющих скорости ветра, найденные из радиозондовых измерений 06.11.2008 в атмосфере над районом Desert Rock

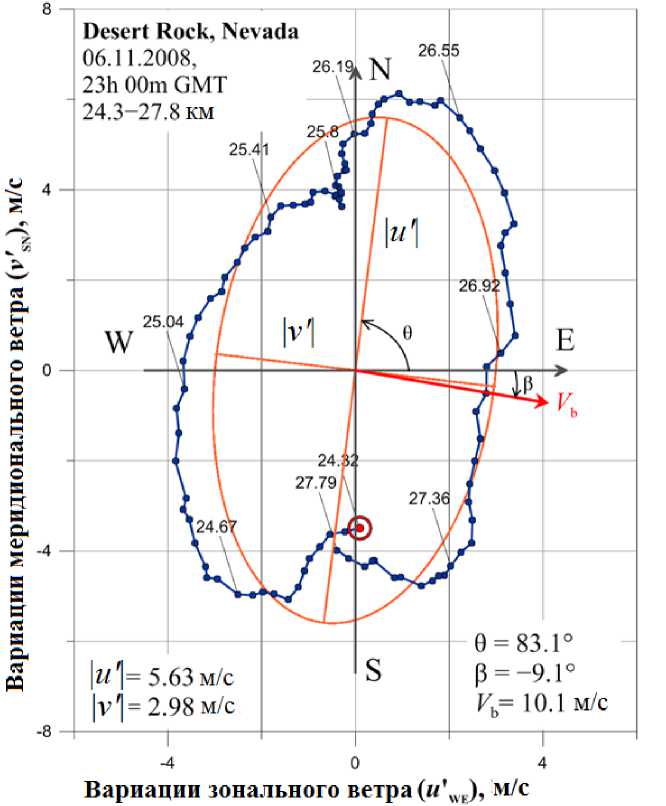
Рис. 4. Годограф вариаций скорости ветра, построенный для интервала высот 24.3–27.8 км

Внутренние волны будут только тогда воздействовать на невозмущенный ветер или приводить к перемешиванию составляющих в атмосфере, когда возникает волновая диссипация энергии. Полагают, что динамическая и конвективная неустойчивости являются основными процессами, приводящими к диссипации [Fritts, 1989; Fritts, Alexander, 2003] , однако имеют место и другие механизмы (молекулярная диффузия, радиационный демпинг, нелинейные взаимодействия). Конвективная или динамическая неустойчивость приводит к обрушению ВГВ, когда ее амплитуда превышает определенный порог. С помощью выражения (7) мы вычислили пороговую амплитуду а . 0.92 для сдвиговой неустойчивости, которая является определяющей для низкочастотных ВГВ с ω~ f [Fritts, 1989] . Из-за существования пороговых амплитуд механизмы насыщения становятся нелинейными, поэтому важно знать величины реальных волновых амплитуд в экспериментах. Используя выражения (8), мы получили две независимые оценки волновой амплитуды а е . 0.43 и а u . 0.40, которые хорошо согласуются между собой. Это указывает на высокое качество анализируемых данных по температуре и скорости ветра, а также свидетельствует, что поляризационное соотношение (4) удовлетворяется. Из выражений (9) двумя разными способами были найдены оценки степени насыщения ВГВ d _e . 0.47=47 % и d _u . 0.44=44 %.

Проведенный анализ свидетельствует о том, что предлагаемый метод позволяет надежно идентифицировать следы ВГВ в данных радиозондовых измерений, а также определять характеристики и степень насыщения внутренних волн в атмосфере Земли без привлечения каких-либо предположений. При радио-затменном мониторинге волновой активности в атмосферах планет [Gubenko et al., 2008b, 2011; Губенко и др., 2012, 2015] используется предположение о насыщении волновой амплитуды. Полученные результаты показывают, что положение о насыщении ВГВ выполняется не всегда, что может приводить к систематическим погрешностям и смещению восстанавливаемых волновых характеристик. В частности, оценки собственной частоты могут систематически занижаться, а значения горизонтальной длины волны — завышаться.

Работа выполнена при частичной поддержке Программы 28 Президиума Российской академии наук. Авторы выражают благодарность двум анонимным рецензентам статьи за содержательные и конструктивные замечания.