Дидактическая инженерия: цифровая модель педагогического тестирования

С точки зрения развития цивилизации, образовательные системы любой эпохи нацелены на решение проблем этой эпохи. При этом, образовательные системы одних стран это делают лучше, и как результат экономики этих стран, имеют большие значения показателя валового продукта за счет эффективных образовательных систем, научных достижений, производительности труда и других ресурсов. С исторической точки зрения, образовательные системы являются одним из основных «толкающими вперед» механизмов развития цивилизации.

Стоит подчеркнуть, что до нашей эпохи человек решал все проблемы в пространстве с двумя степенями свободы, т.е. он решал их в когнитивно – реальном пространстве жизнедеятельности. В нашу эпоху добавилась еще одна степень свободы, и пространство жизнедеятельности человека стало с тремя степенями свободы: когнитивное, виртуальное, реальное. Этот факт позволяет использовать системы, основанные на технических средствах, Web коммуникациях и «искусственном интеллекте» во всех сферах жизни. Бесспорно, что эти системы из техносферы внедряются через образовательную систему в качестве интернет вещей в быт и в экономику. За рубежом эти системы коротко назвали smart системами. Таким образом, эта новая степень свободы развития цивилизации на практике позволила во многих странах построить «цифровую экономику» с высокими значениями показателей производительности труда. В связи с этим, очевидно, миссия образовательных систем нашей эпохи состоит в том, чтобы научить людей жить и работать в обществе с «цифровой экономикой». Из сказанного следует, что «Дидактическая инженерия» как наука об организации обучения это продолжение «Дидактики» в пространстве жизнедеятельности с тремя степенями свободы, востребованное в силу исторической необходимости, на основе которого строятся дидактические smart системы нового поколения.

При решении проблем, знания человека в зависимости от качества его сформированности (информационной полноты, структурной целостности) проявляются через его «мыслительные умения» [1–3]. В целом, при столкновении человека с проблемой определенной сложности, которую необходимо ему решить «мыслительные умения» являются его инструментальным средством формирующим мотив, цель, систему возможностей и ограничений, образ ожидаемого результата и т.д. Таким образом, «мыслительные умения» являются генератором, формирующим среду окружения (контекст) проблемы [4, 5], которая представляет собой ментальную модель [6] окружающей среды проблемы. В свою очередь, проектно-конструктивные способности [7] человека определенного уровня развития, необходимые для решения проблемы в полной мере могут проявиться только в среде этой ментальной модели решаемой проблемы. Очевидно, что если ментальная модель среды проблемы, построенная в когнитивной сфере человека неадекватно реальной среде из-за недостатка достоверной информации или плохого качества сформированости его знаний, то его проектно – конструктивные способности не имеют возможность проявиться в полной мере как интеллектуальный инструмент для решения рассматриваемой проблемы в этой среде .

Численные значения интегративных показателей, характеризующих качество сформированности знаний человека, являются латентными, поэтому значения показателей информационной полноты и структурной целостности его знаний, можно оценить только через педагогический тест. Как известно, значения латентных показателей могут быть оценены с разной точностью и только опосредовано, через специально построенные разного рода тесты [8-10]. При этом, эти результаты, с разной надежностью, объективно отражают уровень развития «мыслительных умений» учащегося [11-15], которые он как интеллектуальный инструмент использует при решении проблем. Бесспорно, что это обстоятельство сильно влияет на значение показателя эффективности любой дидактической системы.

В целом, потребность решения проблем проектирования эффективных автоматизированных дидактических систем нового поколения [16-20] on-line обучения на основе цифровых технологий [21-25], вызвало необходимость использования инженерного подхода для их решения. В свою очередь, это обстоятельство породило в методологии дидактики новое направление «Дидактическая инженерия» [26-31], в которой на основе системного анализа [32-35] разрабатываются модели, нацеленные на автоматизированную организацию учебной деятельности и контроля качества результата с использованием элементов «искусственного интеллекта» [36-38].

Знания и способности

Рассмотрим знание как интеллектуальное инструментальное средство (ресурсы), позволяющую решить какую-то проблему. С системной точки зрения, рассмотрим процесс (деятельность) решения проблемы сложности S человеком, имеющим определенный деятельностный потенциал. Для установления роли и значимости этого ресурса в этом потенциале используем системный анализ как методологию, которая через методы моделирования (вербальное, математическое, табличное, графическое, имитационное) позволяет познать системы с разных точек зрения согласно цели исследования. На рисунке 1 приводится универсальная модель структуры организации деятельности, которую человек использует при решении любой проблемы. По этой модели решение проблемы происходит следующим образом: ВХОД (проблема сложности S) преобразуется им через ДЕЯТЕЛЬНОСТЬ в ВЫХОД (со случайным результатом X – решил проблему или нет) под УПРАВЛЕНИЕМ (проектно – конструктивных (ПК) – способностей определенного уровня развития) с помощью МЕХАНИЗМА (ресурсы: знания о среде проблемы определенного качества сформированности). На этом же рисунке и показано закономерность, как значение показателя на шкале 1 ограничивает на шкале 2 возможность проявления в полной мере ПК-способностей человека при решении проблемы.

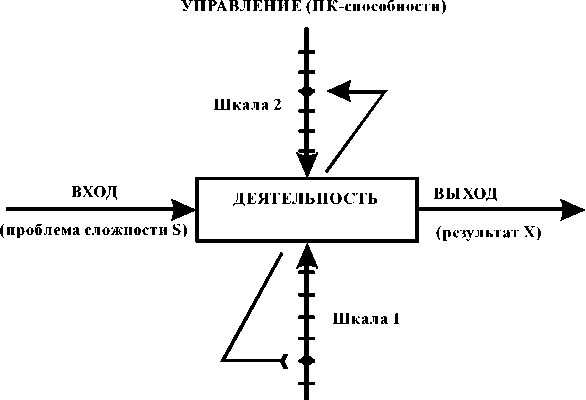
МЕХАНИЗМ (ресурсы: знание)

Рис. 1. Модель структуры организации деятельности по решению проблемы

Таким образом, результаты анализа по модели и литературных источников по психологии (Б. Блум, В. П. Беспалько, Л. С. Выготский, А. А. Леонтьев, С. Л. Рубинштейн) показывают, что при решении проблем, знания как результат «внутренней деятельности» человека представляют собой механизм (ресурсы) для проявления в когнитивной сфере его «мыслительных умений». В свою очередь, «мыслительные умения», сами являются ресурсами для поддержки проектно -конструктивных способностей во «внешней деятельности», которые проявляется как практические умения при решении проблем.

Следует подчеркнуть, что алгоритмы, построенные на базе цифровой модели тестирования, показывают объективную оценку качества сформированности знаний обучающегося с надежностью более 95% в соответствии с таксономией Б. Блума.

Модель организации и формирования знаний

Знание это переработанное и заново структурированное через сознание человека информация. В модели этот процесс можно представить, так как показано на рис. 2.

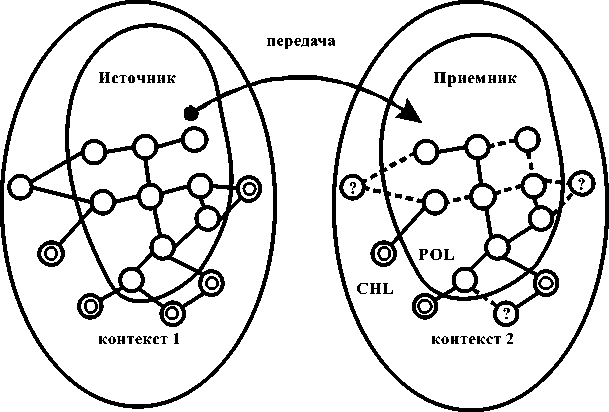
Рис. 2. Процесс формирования знаний в полноте и целостности

Из «источника» информация с определенной структурой (на рисунке показано, что только со структуры из внутреннего контура «источника») передается в «приемник» и воспринимается там, в определенной полноте (мера полноты восприятия, т.е. значение показателя POL – качества восприятия меняется от 0 до 100 %). Одновременно с процессом восприятия информации происходит процесс синтеза знаний с организацией новой структуры, т.е. воспринятая информация «встраивается» в контекст (в мировоззренческую модель) «приемника». Очевидно, чем ближе мировоззренческая модель «приемника» к модели «источника», тем более целостна структура организации информации у «приемника». При этом, меру качества целостности (валидности) новой структуры относительно структуры «источника», обозначим через CHL (изменяется от 0 до 100 %). Таким образом, в целом, качество сформированности знаний «приемника», т.е. качество его мировоззренческой модели в какой-то предметной области, можно охарактеризовать только парой (комплексом) показателей {POL, CHL} с их численными значениями [4-10, 15]. Из сказанного следует, что передать знания от одного человека к другому, даже в рамках предметной области, практически невозможно, т.к., в основном, «источник» физически (как бы он не старался) не может передать знания без ее контекста, т.е. без своей мировоззренческой модели.

Модель организации деятельности по решению проблем

В течение всей жизни, человек, как правило, нацелен на решение каких-то проблем и обучению их эффективному решению. При этом, роль и значимость знаний в процессе решении проблем можно понять только с системной точки зрения.

Как не парадоксально, все люди организуют свою деятельность по решению проблем одним и тем же способом, который состоит из трех основных операций. 1. Операция А – формализация проблемы, т.е. создания образа проблемы в когнитивной сфере и преобразование ее в среде своих знаний в задачу согласно цели. 2. Операция

В – конструирование плана решения задачи на базе имеющихся знаний. 3. Операция С – исполнение плана в какой-то среде на базе знаний с использованием других ресурсов. Модель организации деятельности по решению проблемы можно представить через диаграмму SADT [40]. Как уже было отмечено (см. рис. 1), что в общем случае, любая система по модели SADT функционирует так: ВХОД перерабатывается в ВЫХОД под определенным УПРАВЛЕНИЕМ с помощью определенного МЕХАНИЗМА. Разумеется, качество и количество материала на ВЫХОДЕ, т.е. результата будет зависеть от качества и количества материала на ВХОДЕ, качества организации УПРАВЛЕНИЯ и МЕХАНИЗМА на базе имеющихся ресурсов определенного количества и качества. Произведем декомпозицию (см. рис. 1) и распишем ДЕЯТЕЛЬНОСТЬ по операциям, т.е. операции формализация проблемы с преобразованием в задачу, конструирование плана (алгоритма) решения задачи, исполнение плана в какой- то среде. При этом, как уже было сказано, мера возможного проявления АВС способностей в конкретном случае будет ограничено знаниями о среде проблемы.

СПОСОБНОСТИ (управление)

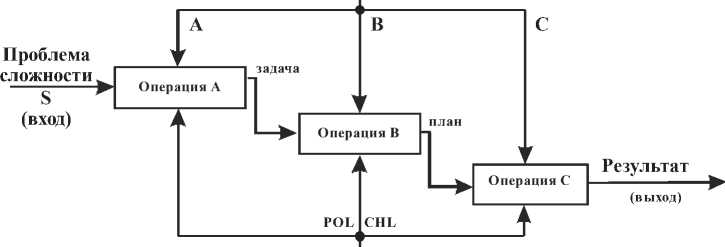
ЗНАНИЯ (механизм)

Рис. 3. Модель организации деятельности по решению проблем

Обозначим через X случайное событие (результат), что определенный человек R решить проблему сложности S. Из модели следует, что вероятность P(X), что R решит проблему зависит от уровня развития его формализационной (А), конструктивной (В), исполнительской (С) способностей и качество сформированности его знаний {POL, CHL}, а также других ресурсов, которые в рамках данной модели учитываться не будут. В рассматриваемом случае, формально вероятность P(X) можно представить через функционал F(*)

P(X) = F(A, B, C, POL, CHL, S).

Очевидно, что комплекс показателей

Pot (t) = {A, B, C, POL, CHL} с их конкретными значениями, в целом, характеризует уровень развития деятельностного потенциала человека X на момент времени t. Исходя из этого, можно записать так

P(X) = F(Pot (t), S).

Таким образом, т.к. P(X) всегда меньше или равно единицы, то деятельностный потенциал человека Pot (t) всегда ограничен сложностью проблем S, которые он с вероятностью P(X) = 1 способен решить.

Следует особо подчеркнуть, что знания человека нельзя отделить от его способностей, на практике они проявляются в совокупности как разного рода умения, т.е. знания проявляются через «мыслительные умения», т.е. как умения запоминать и воспроизводить, анализировать, информацию, синтезировать новые знания [1-3]. Способности проявляются на основе «мыслительных умений» как практические умения, т.е. как умения сделать что-то конкретное: решить проблему той или иной сложности, например, построить дом той или иной величины и качества и т.д. В теории деятельности А.Н. Леонтьева, С.Л. Рубинштейна выделяется и подчеркивается необходимость согласованности «внутренней» и «внешней» деятельностей для получения необходимого результата, в конкретном случае, решения проблемы.

Очевидно, что по состоянию уровня развития деятельностного потенциала Pot (t) человека можно построить прогноз, до какой сложности S проблему может решить человек с большой вероятностью из какой- то предметной области на определенный момент времени. В то же время, состояние развития потенциала любого человека можно отобразить в модели в псевдо – фазовом пространстве [4, 23, 36]. В этом пространстве, изменения значений показателей A, B, C, POL, CHL показано как изменение траектории уровней развития человека во времени (рис. 4).

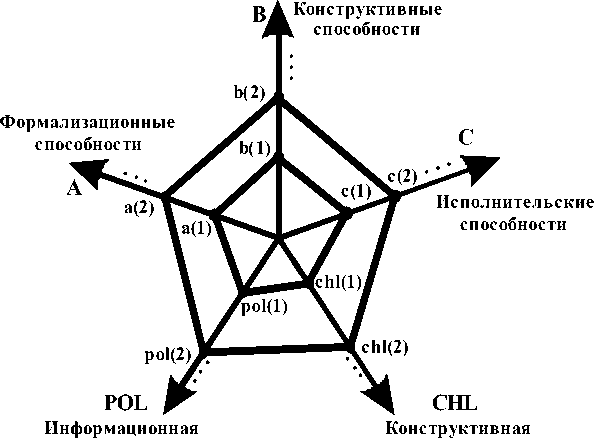
полнота знаний                  целостность знаний

Рис. 4. Псевдо – фазовое пространство развития деятельностного потенциала

В псевдо – фазовом пространстве, так же можно отобразить сложность проблемы, которую (согласно прогнозу) человек с определенным потенциалом может решить, с определенным значением вероятности (надежности). Приведем пример. В псевдо – фазовом пространстве рассматривается ситуация (рис. 5). На этом рисунке сложность проблемы изображен как треугольник с определенными координатами вершин (sa, sb, sc) и с их конкретными значениями, где sa = 3, sb = 6, sc = 9 – трудности формализации, конструирования, исполнения решения проблемы, по мнению эксперта. Известен деятельностный потенциал Pot (t) = {A = a = 5, B = b = 7, C = c = 3, POL = pol = 0,8, CHL = chl = 0,5} человека, решающего проблему. В этой ситуации возникает математическая задача: требуется спрогнозировать, с какой вероятностью человек решит проблему. Подробный метод решения это задачи изложен в работе [22]. В этой работе решение приведем только вкратце.

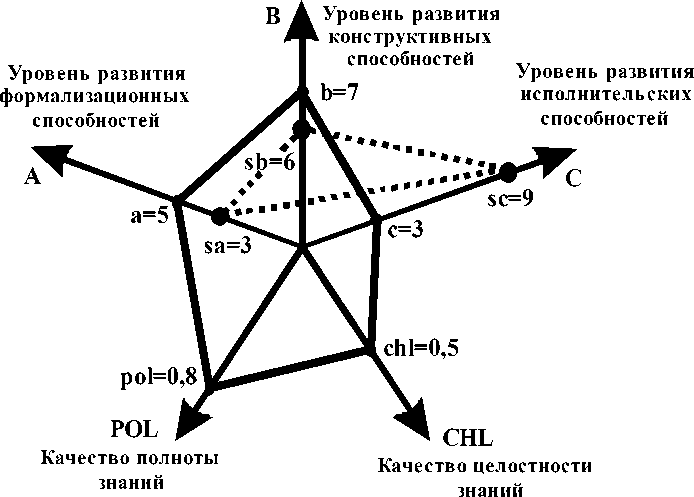
Рис. 5. Эпизод ситуации расположения значений различных показателей в фазовом пространстве

Решение задачи: RA – случайное событие, что человек сможет адекватно формализовать проблему и преобразовать в задачу, тогда вероятность P(RA) = 1 (т.к. a > sa); аналогично, P(RB) = 1 (т.к. b > sb); P(RC) = 1/3 (т.к. с / sc). На рис. 5, показано, что качество сформированности знаний человека, решающего проблему KZ = SQR(0,8 * 0,5) = 0,64. Вероятность (шанс, т.к. RA, RB, RC – зависимы) решить проблему, вычисляется как вероятность произведения независимых случайных событий, т.е. P(RA* RB*RC) = P(RA) * P(RB) * P(RC) * KZ = 1/3 * 0,64 = 0,213. Таким образом, у человека, имеющего деятельностный потенциал (А = 5; В = 7; С = 3), вероятность полностью решит проблему сложности (SA = 3; SB = 6; SC = 9) равен P(RA*PB*PC) = 21,3 % из возможных ста процентов, т.е. вероятность решить эту проблему примерно равна P = 0,213.

В целом, на этой теоретической основе [16] проектируются дидактические системы нового поколения [20, 21, 28, 29]. Главной особенностью дидактических систем нового поколения с цифровыми технологиями является то, что они позволяют создать образовательную среду целенаправленного управляемого развития обучающихся. В этой среде можно эффективно управлять (в автоматическом или в ручном режимах) процессом развития (повышения уровня развития) деятельностного потенциала обучающегося, в каком-то промежутке времени от t1 до t2. Как было показано в модели (рис. 4, рис. 5), это означает, что на базе их создается образовательная среда, в которой студент при старании и с учетом его природных особенностей, может развить свой деятельностный потенциал до требуемого уровня. На рисунке 4 отображена цель развития через обучение. Там показано, что студент должен и может (согласно своей природе и предыдущему состоянию развития) развить свой деятельностный потенциал со значениями показателей Pot(t1) = {a(1), b(1), c(1), pol(1), chl(1)} до потенциала со значениями показателей Pot(t2) = {a(2), b(2), c(2), pol(2), chl(2)}.

Цифровая модель таксономии Блума – Беспалько

В модели, на основе показателей качества информационной полноты, усвоенной информации и качества структурной ее целостности, можно выделим несколько классов качества сформированности знаний человека. В настоящее время известно множество разнообразных вариантов таксономий (классификаций) качества сформированности знаний учащихся. Наиболее популярными являются варианты, предложенные Б. Блумом и В.П. Беспалько [1-3]. Хотя в этих вариантах классификаций имеются различия, но, в целом, при некоторой их модификации, по мнению авторов, их можно объединить. В объединенной классификации, рассмотрим вариант с четырьмя классами качества сформированности знаний учащихся. В каждом конкретном случае на актуальный момент времени, класс качества сформированности знаний обучающихся можно определить через педагогический тест. Достоверность этого способа обосновывается так. По результатам практик и исследований установлено [3], что принадлежность знаний обучающегося к определенному классу идентифицируется, опосредовано через уровень развития его «мыслительных умений», т.е. каждому классу качества сформированности знаний можно поставить в соответствие его «мыслительные умения» определенного уровня развития. Поэтому на практике в качестве инструмента для оценки уровня развития «мыслительных умений» предлагается тест и уже через оценку качества ответов на вопросы теста, устанавливается уровень развития «мыслительных умений» обладателя знаний, а также соответствующий класс качества сформированности знаний обущающихся. Это соответствие знаний – умений по таксономии Блума – Беспалько выглядит следующим образом:

1. Знание – воспроизведение. Это первый класс качества сформированности знаний учащегося. Его обладатель может (умеет) только воспроизвести в определенной полноте усвоенную информацию. 2. Знание – понимание. Это второй класс качества сформированности знаний. В этом классе его обладатель, умеет («мыслительные умения») усвоенную в определенной полноте информацию не только воспроизвести, но и переформатировать ее, например, перевести с одного языка на другой, сделать чертеж, пояснить смысл и т.д. 3. Знание – применение. Это третий класс качества сформированности знаний. В этом классе его обладатель в интеграции со своими способностями умеет променять свои знания для решения практических задач, например, способен сделать анализ проблемной ситуации, сконструировать план решения и получить требуемый результат. 4. Знание – синтез. Это четвертый класс качества сформированности знаний. Обладатель знаний этого класса качества умеет системно мыслить. Это позволяет ему на базе своих знаний и при условии высокого уровня развития его способностей разрешать сложные проблемы, т.е. синтезировать новые знания и объекты, а также проводить экспертизу качества уже созданных объектов и технологий, решать задачи прогноза поведения больших и сложных систем.

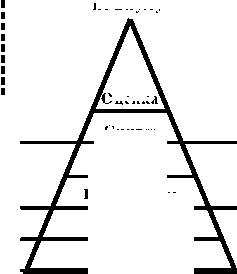
На практике, через данные статистики, цифровой показатель качества сформированности знаний Z человека с конкретными значениями, полученными в результате педагогического теста [6-9] Z = {POL= pol > 0, CHL = chl > 0} можно соотнести с «мыслительными умениями» на «пирамиде» таксономии Б. Блума (рис. 6). Для этого необходимо оцифровать «мыслительные умения» по классификации Б. Блума по следующему алгоритму: 1. Вычислить значение CZ – среднее геометрическое по формуле CZ = SQR(pol * chl), т.е. сделать мультипликативную свертку показателей POL и CHL в единый показатель CZ через их среднее геометрическое. 2. Установить статистически обоснованное (по критерию согласия Пирсона) устойчивое соответствие между качественной шкалой (классом по Блуму – Беспалько) и цифровой шкалой. Таким образом, качество сформированности знаний по классификации Блума – Беспалько, можно обоснованно преобразовать в метрическую (цифровую) шкалу. Согласно статистическим данным, можно установит связь с оценками «достижений» в пятибалльной шкале, которая используется в образовательном делопроизводстве в РФ и в ряде других стран.

Номера классов

качества сформированности знаний по таксономии Блума

Уровни качества проявления “мыслительных умений” по Блуму

Оценка

Синтез

Анализ

Применение

Понимание

Знание

Оцифрованная  Пятибальная шкала качества     шкала

“мыслительных  “достижений”

умений” в интервале

(0,1]

Незнание

0,87<=CZ         5

i I i i

0,74<=CZ<=0,86;4

i I i

0,60<=CZ<=0,73!3

i

_______________________________I______________

CZ<0,602

Рис. 6. Оцифрованная шкала «мыслительных умений» по таксономии Б. Блума

Модель организации теста по цифровой технологии

Рассмотрим конкретную ситуацию. Допустим, что on – line курс, в рамках которого студент должен освоить какую–то компетенцию, состоит из пяти разделов. Будем считать, что если показатель качества сформированности, т.е. величина CZ = SQR(pol * chl) знаний студента, например, в рамках этого курса больше 80% с надежностью HZ не менее 95%, то количественная оценка качества получена, и он может получить соответствующий сертификат о качестве сформированности знаний в этой компетенции. В свою очередь, это факт гарантирует проявление его соответствующих «мыслительных умений» при решении проблем с надежностью не менее 95%.

Как уже отмечалось, что показатели POL, CHL являются латентными и непосредственно их измерить нельзя. Поэтому, их значения можно выявить только опосредованно через специально организованную технику педагогического тестирования, нацеленного на выяснение уровня «мыслительных умений» студента. Разумеется, это можно сделать только после освоения компетенции в рамках on – line курса. Структура организации цифровой модели педагогического тестирования приводится на рисунке 7.

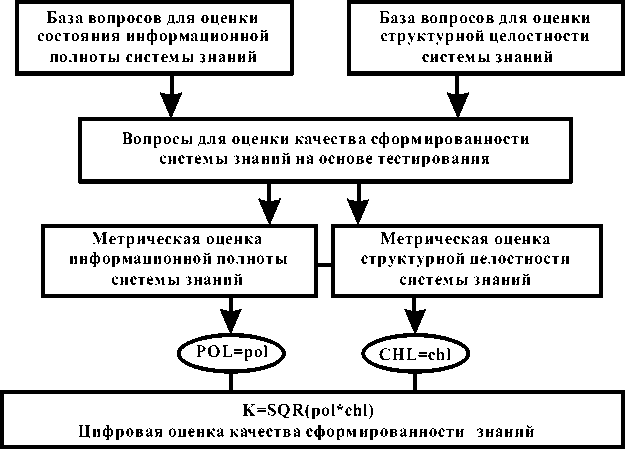
Рис. 7. Структура организации цифровой модели тестирования

Организация базы вопросов для оценки информационной полноты знаний. Структуру организации базы вопросов для оценки информационной полноты системы знаний студента (показатель POL) формируется исходя из ситуации. Напомним, что в рассматриваемой ситуации on – line курс состоит из 5 разделов. Значение показателя качества полноты знаний студента, т.е. значение POL можно оценить из результата ответов студента. Из требования надежности результата тестирования следует, что вариант контрольного задания (билет) должен содержать минимум 10 вопросов. Это позволяет, сформировать билет из расчета по 2 вопроса из 5 разделов курса. При этом вопросы должны быть определенной сложности и ответы на них должны выявить «мыслительные умения» студента, соответствующие первому и второму уровней сформированности знаний студента по классификации (таксономии) Блума – Беспалько. Из сказанного следует, что база вопросов в оцифрованном виде для оценки информационной полноты системы знаний студента, должен иметь формат, как показано на рисунке 8. На рисунке приводится только первый вариант билета организованному по этому формату.

№ варианта	№ вопроса	№ раздела	Вопрос Р(*,*)	Сложность вопроса S(*,*)
1	1	1	Р(1,1)	S(1,1)=0,5
1	2	1	Р(1,2)	S(1,2)=1
1	3	2	Р(2,1)	S(2,1)=0,7
1	4	2	Р(2,2)	S(2,2)=0,9
1	5	3	Р(3,1)	S(3,1)=0,5
1	6	3	Р(3,2)	S(3,2)=1
1	7	4	Р(4,1)	S(4,1)=0,5
1	8	4	Р(4,2)	S(4,2)=1
1	9	5	Р(5,1)	S(5,1)=0,8
1	10	5	Р(5,2)	S(5,2)=1

Рис. 8. Формат организации базы вопросов для оценки качества информационной полноты знаний студента

Отметим, что в первом столбце таблицы базы вопросов указывается номер варианта тестового задания. Таким образом, если требуется, например, 25 вариантов заданий, то база состоит из 25 таких однородных индивидуализированных таблиц, которые в процессе тестирования формируются случайным образом. Через Р(*,1) и Р(*,2) обозначены вопросы, для оценки качества информационной полноты системы знаний студента, усвоенных им в рамках on – line курса. Еще раз напомним, что для ответа на эти вопросы студенту необходимо и достаточно обладать «умственными умениями» соответствующему первому и второму классам по качественной шкале таксономии Блума – Беспалько.

Оценка сложности вопроса теста в системе профессиональной трудности. Очевидно, с наибольшей вероятностью (достоверностью) объективно оценить сложность информационного материала: проблемы, задачи, вопроса в системе реального времени, может только эксперт (группа экспертов [8]). При этом бесспорно, что согласованная оценка этой сложности группой экспертов, покажет по вероятности лучший результат, т.е. будет ближе к объективной оценке сложности. Следует так же подчеркнуть, что других способов оценки сложности информационного материала, т.е. проблемы, задачи, вопроса, в системе реального времени, кроме экспертной оценки (на сегодняшний день) просто не существует. В то же время задачу оценки сложности информационных материалов в образовательном пространстве во всем мире, как правило, решает преподаватель (субъективная оценка). Разумеется, это было допустимо, когда преподаватель может выступать в роле эксперта и управлять учебным процессом, исходя из своей оценки сложности. Автоматизация учебного процесса с «потерей» преподавателя – эксперта, например, обучение через on – line курс, привело образовательное пространство почти в хаос при оценке качества сформированности знаний, а соответственно «мыслительных умений» студента. Разумеется, речь не о том, что надо вернуться к классической системе обучения. Переход образовательного пространства в цифровой формат это объективная закономерность, т.е. веление времени и с этим надо обязательно считаться, но при этом необходимо избавится от хаоса и ввести в образовательном пространстве порядок с точки зрения оценки сложности. Без преувеличения, можно утверждать, что введение численной оценки сложности учебного материала в единой системе профессиональной трудности (назовем это в системе PD) позволит организовать полноценную подготовку через автоматизированные дидактические системы с цифровыми технологиями обучения с гарантированной оценкой качества этой подготовки. Как это можно сделать на практике покажем на примере. В данных, приведенных на рисунке 8, сложность вопроса S(*,*) задается в условных единицах в системе профессиональной трудности (PD). В этой таблице, например, сложность вопроса Р(3, 1) = S(3, 1) = 0,5, т.е. сложность этого вопроса равна 0,5 условных единиц в системе PD. По факту это означает, что эксперт на этот вопрос сам может ответить за 0,5 минуты своей работы, т. е. 0,5(мин / раб) это – трудоемкость работы эксперта. Очевидно, что эксперт сложность S – информационного материала оценивает через свою «субъективную» трудность T, но бесспорно, что значение его оценки T будет ближе к S, чем все остальные субъективные оценки не специалистов. Можно также выдвинуть гипотезу, что во всем образованном мире, все эксперты покажут примерно одинаковый результат. Достоверность этой гипотезы не раз подтверждалось. К сожалению, только в локальном масштабе при небольших выборках. Ну, все же, это в определенной мере (в зависимости от данных статистики) является основанием возможности введения в образовательное пространство единой системы профессиональной трудности, т.е. системы PD для оценки сложности информационного материала. Следует отметить, что в более широком смысле, систему PD можно использовать для оценки сложности любого информационного объекта, т.к. принятое измерение в «байтах» характеризует информационный объект только с точки зрения объема информации и никак не характеризует с точки зрения сложности этого объекта.

Оценка качества информационной полноты знаний через тест. Конкретно, значение оценки качества (в процентах) информационной полноты знаний студента, т.е. значение показателя POL(1), вычислим по формуле

POL(1) = (R1/R2) * (R3/SS) + (R4/R2) * (R5/SS)

где введены обозначения:

R1 – количество правильных ответов на вопросы типа Р( *, 1) первого уровня сложности. Например, студент правильно ответил на 3 вопроса из 5 первого уровня сложности, это означает что R1 = 3.

R2 – общее количество всех вопросов первого уровня сложности, например, в рассматриваемом случае R2 = 5.

R3 – суммарная сложность вопросов типа Р(*, 1) на которые студент дал правильный ответ. Допустим, студент правильно ответил на вопросы Р(1,1), Р(2,1), Р(5,1), тогда R3 = S(1,1) + S(2,1) + S(5,1) = 0,5 + 0,7 + 0,8 = 2.

R4 – количество правильных ответов на вопросы типа Р(*, 2) второго уровня сложности. Например, студент правильно ответил на 2 вопроса из 5 второго уровня сложности R4 = 2.

R5 – суммарная сложность вопросов типа Р( *, 2) на которые студент дал правильный ответ. Допустим, студент правильно ответил на вопросы Р(1,2), Р(2,2), тогда R5 = S(1,2) + S(2,2) = 1 + 0,9 = 1,9.

SS - суммарная сложность всех вопросов теста. Например, в рассматриваемом случае SS = 8.

Для ясности, рассмотрим два примера вычисления значения показателя POL(1).

Пример 1. Рассчитаем значения POL(1) для случая, по данным приведенным по ходу трактовки обозначений, т.е. R1 = 3; R2 = 5; R3 = 2; R4 = 2; R5 = 1,9; SS = 8. POL(1) = (3/5) * (2/8) + (2/5) * (1,9/8) = 0,245. В итоге, полнота, усвоенной информации студентом в рамках on – line курса составляет всего 24,5% из 100% возможных, т.е. 24,5% это подтвержденное значение показателя качества полноты его знаний с надежностью не менее HZ = 95%, из воспринятой им информации. Таким образом, по таксономии Б. Блума, студент может показать «мыслительные умения» только из нулевого класса, после освоения компетенции через on-line курс.

Пример 2. Рассмотрим случай, когда студент освоил компетенцию на основе on – line курса и в рамках этого курса ответил правильно на все вопросы теста, т.е. R1 = 5; R2 = 5; R3 = 3; R4 = 5; R5 = 5; SS = 8. POL(1) = (5/5) * (3/8) + (5/5) * (5/8) = 1. В этом случае, показатель качества полноты, усвоенной информации студентом в рамках on – line курса составляет 100% с надежностью не менее HZ = 95%, но выдавать сертификат (как часто это делают) без проверки структурной целостности его знаний нельзя, т.к. его «мыслительные умения» подтверждены только для 1 класса.

Организация базы вопросов для оценки структурной целостности знаний. Как было сказано ранее, что знание это переработанное и заново структурированное через сознание человека информация, т.е. знание человека это продукт синтеза в его когнитивной сфере воспринятой им информации. Качество сформированности знаний характеризуется только в комплексе его полнотой и структурной целостностью. Высокое качество целостности структуры (характеризующий показатель CHL) организации знаний человека рассматривается, прежде всего, с точки зрения возможности применения этих знаний в совокупности со способностями в практической деятельности в рамках (согласно цели) освоенной компетенции, например, для разрешения проблем. Это означает, что при тестировании, через специально сформулированные вопросы третьего, четвертого класса (уровней) сложности, которые соответствуют этим же уровням в шкале «умений» по таксономии Блума – Беспалько, должны проявиться ожидаемые «мыслительные умения» студента. Разумеется, что вопросы должны быть такого качества, чтобы правильные ответы на них позволили бы оценить способность

(умственные умения) анализировать и синтезировать новые знания на основе усвоенной студентом информации. Если студент это умеет, то это означает, что качество структурной целостности его системы знаний и уровень развития его способностей достаточно для разрешения проблем в рамках, освоенной им компетенции. Из этого следует, что при условии надежности результата тестирования ему можно выдавать сертификат. Из контекста следует, что база вопросов для оценки показателя структурной целостности системы знаний студента, должен иметь формат (рис. 9).

№ варианта	№ вопроса	№ раздела	Вопрос Н(*,*)	Сложность вопроса S(*,*)
1	1	1	Н(1,1)	S(1,1) = 4
1	2	1	Н(1,2)	S(1,2) = 6
1	3	2	Н(2,1)	S(2,1) = 3,5
1	4	2	Н(2,2)	S(2,2) = 5
1	5	3	Н(3,1)	S(3,1) = 4
1	6	3	Н(3,2)	S(3,2) = 6,5
1	7	4	Н(4,1)	S(4,1) = 4,5
1	8	4	Н(4,2)	S(4,2) = 6
1	9	5	Н(5,1)	S(5,1) = 3,5
1	10	5	Н(5,2)	S(5,2) = 7

Рис. 9. Формат организации базы вопросов для оценки структурной целостности знаний студента

Значение показателя CHL структурной целостности системы знаний человека вычисляется по формуле

CHL(1) = (R1/R2) * (R3/SS) + (R4/R2) * (R5/SS)

Все переменные при расчетах значения CHL имеют тот же смысл, что использовались при расчете значения POL, с учетом того, что вместо вопросов Р(*, *) используются вопросы Н(*, *) соответственно с другой сложностью S(*,*). Следует также учесть, что любой вариант билета из базы вопросов для оценки структурной целостности системы знаний формируется по – другому. Это связано с установленной закономерностью [9, 10], которая звучит так: если сложность вопроса больше S(*,*) = 1 (мин/раб) в шкале PD, то для ответа на этот вопрос студенту потребуется 3*S(*,*) (мин/раб). Например, вопрос Н(5,2) в системе PD имеет сложность S(5,2) = 7, то при расчетах для ответа на этот вопрос студенту отводится 21(мин/раб). Также следует учесть, общеизвестный факт уставания студента, т.е. общее время тестирования не должно превышать 45 (мин/раб). Рассмотрим пример сформированного тестового задания (вариант №1). Задание состоит из двух билетов или объединенного одного билета, т.е. билет 1 (см. рис. 2) и билет 2 (см. рис. 10).

№ варианта	№ вопроса	№ раздела	Вопрос H(*,*)	Сложность вопроса S(*,*)
1	9	5	Н(5,1)	S(5,1) = 3,5
1	10	5	Н(5,2)	S(5,2) = 7

Рис. 10. Формат вопросов для оценки структурной целостности знаний студента

Таким образом, билет 2 сформирован случайным образом и предназначен для проверки «мыслительных умений» студента на примере раздела 5 из on – line курса. Продолжительность Т(студ) тестирования студента будет рассчитана по последующей формуле

Т(студ) = S(1,1) + S(1,2) + S(2,1) + S(2,2) + S(3,1) + S(3,2) + S(4,1) + S(4,2) + S(5,1) + S(5,2) + 3 * (Н(5,1) + Н(5,2)) = 8 + 31,5 = 39,4 (мин/раб).

Оценка результатов тестирования в единой цифровой шкале в системе профессиональной трудности. Например, человек после тестирования имеет такие значения показателей (POL = 98%; CHL =5%), т.е. согласно классификации « умственных умений» по таксономии Блума – Беспалько, этот человек в рамках курса способен (умеет) выдать обратно почти полностью, т.е. 98% (0,98) усвоенную им в рамках курса информацию, понимает ее и может переформатировать. При этом, использовать, свои знания для анализа и синтеза (согласно результату теста, всего 5 % его знаний структурировано) он не может. Поэтому маловероятно, что он способен решить какую – то проблему на практике. Через показатель CZ обозначим единую характеристику качества сформированности знаний человека, полученную им по результатам теста. Значение величины CZ вычислим по следующей формуле

CZ = [(max1 * POL + max2 * CHL) / (max1 + max2)] *100% где max1, max2 – соответственно значения S(*, *) максимальной сложности вопросов типа POL и CHL. Значение величины CZ имеет следующий смысл: в системе профессиональной сложности (PD) с порядком сложности теста (max1 + max2), тестируемый показал CZ% качества сформированности своих знаний. Например, после тестирования пять студентов (С1, С2, С3, С4, С5) имеют результаты: С1(POL = 98%; CHL =5%); С2(POL = 95%; CHL = 55%); С3(POL = 60%; CHL =30%); С4(POL = 90%; CHL =80%); С5(POL = 100%; CHL =100%). В системе PD с порядком сложности теста (1+7) = 8, первый студент показал CZ = [(1 * 0,98 + 7 * 0,05) / 8] *100% = 16,6% качество сформированности своих знаний; второй показал CZ = 49,3%; третий показал CZ = 33,75%; четвертый CZ = 81,25%; пятый CZ = 100%.

Очевидно, в системе PD (в рамках предметной области) можно договориться о едином порядке сложности теста и тем самым измерить «близость тестируемого к профессионалу» в едином масштабе. В целом, это наведет определенный порядок в образовательном пространстве, значимо уменьшит дисперсию в оценках качества сформированности знаний в предметной области.

Заключение

Необходимый высокий темп освоения компетенции, качество которой позволяет разрешать сложные проблемы, потребовало организацию «умных» дидактических систем нового поколения с цифровыми технологиями, позволяющими быстро освоить эту компетенцию в on-line (интерактивном) режиме. В работе показано, что качество сформированности знаний человека, во многом, определяют его «мыслительные умения», от которых в комплексе с его проектно – конструктивными способностями определенного уровня развития, зависит значение вероятности: решит или не решит проблему данной сложности этот человек. Умение решать сложные проблемы в системе реального времени одно из главных способностей человека, работающего в государстве с цифровой экономикой. В работе, также показано, что качество сформированности знаний можно оценить только опосредовано, т.е. через проявление «мыслительных умений» при ответах на вопросы теста определенной трудности. Так же показано, что результаты тестирования могут считаться объективными, если вопросы этого теста разделены на два класса заданий. Первый класс – содержит вопросы для оценки качества полноты, усвоенной информации. Второй класс – содержит вопросы для оценки качества целостности знаний, синтезированных через сознание в когнитивной сфере обладателя информации. В первом и во втором классах вопросов учитываются их сложности в единой системе профессиональной трудности, и результаты ответов оцениваются с учетом этих сложностей. Из статистических данных следует, что алгоритмы, построенные на базе цифровой модели тестирования, показывают объективную оценку качества сформированности знаний обучающегося с надежностью более 95% в соответствии с классами по таксономии Б. Блума. На практике этот факт объективности результата является очень значимым, т.к. качество сформированности знаний человека во многом определяет его деятельностный потенциал.