Дифференциация студентов по признаку изменения рейтинговых достижений на основе анализа трендов прогнозных данных

Среди всего многообразия математических моделей в педагогической прогностике [1, 2] выделяются особые модели, способные сами анализировать вновь поступающую информацию, находить в ней закономерности и производить прогнозирование, так называемые нейронные сети - самообучающиеся системы, имитирующие деятельность человеческого мозга [3]. Мониторинг процесса образования на основе функционирующей нейросетевой модели прогноза позволяет осуществить индивидуальный подход к каждому студенту и вносить адресные коррективы в его образовательный процесс, что обеспечивает реальный положительный эффект по критерию успешности усвоения учебного материала каждым студентом [4, 5].

В данном исследовании после накопления определенного объема прогнозной информации индивидуально по каждому из студентов контрольной группы проводится ее анализ с целью подтверждения или отклонения гипотезы о том, что каждая учебная группа представляет собой совокупность отдельных подмножеств студентов, условно разделяемых на три вида по признаку величины тенденции к повышению рейтингового балла в балльнорейтинговой системе (БРС):

• 1)    сильная положительная;

• 2)    слабая положительная, либо слабая отрицательная;

• 3)    сильная отрицательная.

Очевидно, что данные тенденции могут быть выявлены только в динамике изменения рейтинговых достижений студентов. Поскольку полученные нами ранее индивидуальные прогнозные данные высококоррели-рованы с фактическими, то используем именно их для выявления тенденций развития достижений каждого из учащихся. С этой целью построим персональные прогнозные ряды и аппроксимируем их линейными трендами. Выбор линейного тренда обосновывается тем, что требуется определить, по сути, вектор направленности учебной деятельности студента в рамках БРС, и определить положителен он или отрицателен по величине углового коэффициента. Если же его направленность выражена слабо (угловой коэффициент близок к нулю по абсолютной величине), то можно считать, что студент стабилен в своих рейтинговых достижениях.

Практическая ценность подобной процедуры дифференциации может быть объяснена следующим обстоятельством: множество студентов по отношению к учебной деятельности мотивировано различно как по направленности, так и по силе мотивации. Можно сказать, что в данном контексте учебная группа представляется векторным полем. Направление векторов определяет движение отдельных студентов, а в совокупности и группы, к успеху либо неуспеху в учебной деятельности по данной дисциплине.

Выявить данные тенденции можно только в динамике, так как моментные срезы не позволяют судить об их характере. Очевидно, что разные студенты, имеющие в данный мо- мент времени одинаковые баллы, в дальнейшем могут повести себя совершенно различным образом и их моментное рейтинговое равенство может оказаться не более как пересечением двух разнонаправленных трендов. Знание направленности тенденций всей группы в целом и степень ее дифференциации, а также объемы подмножеств позволяют преподавателю правильно спроектировать дальнейший образовательный процесс, внося индивидуальные коррективы для каждого из учащихся.

Апробируем предложенный алгоритм на примере контрольной группы студентов по дисциплине «Математика». Линейные тренды по прогнозным рейтинговым данным были построены по методу наименьших квадратов в пакете Excel MS Office. Множество угловых коэффициентов трендов было обработано пакетом «Описательная статистика» и по результатам построена гистограмма (рис. 1).

(см. таблицу). Выделим группу студентов, имеющих среднее значение рейтингового балла (диапазон от 30 до 70 %), отсекая заведомо высоко успешных и низко успевающих. Расставляя знаки тенденций (знаки угловых коэффициентов трендов) можно сделать вывод о том, что данное множество, однородное по величине рейтингового балла, неоднородно по знакам тенденций. С учетом сказанного, можно с определенной долей уверенности спрогнозировать, что 4 из 12 студентов в ближайшей перспективе ухудшат свои результаты, 3 останутся стабильными, а 5 студентов, скорее всего, улучшат свои достижения.

Таким образом, описанный выше алгоритм выявления скрытых тенденций в индивидуальных учебных достижениях студентов, позволяет произвести дифференциацию внешне однородного множества студентов.

На основе выделения подмножеств студентов с положительной и отрицательными

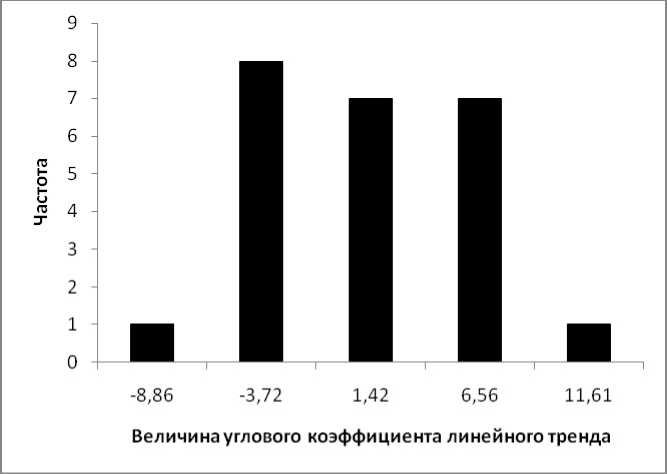
Рис. 1. Гистограмма частот значений угловых коэффициентов линейных трендов

По результатам расчетов можно сделать вывод, что большинство студентов группы (15 из 24) имеют выраженную тенденцию к повышению результатов рейтинга по математике, а 9 из 24, скорее всего, ухудшат свой рейтинг. Именно эта группа из 9 человек и должна являться объектом особого внимания преподавателя по данной дисциплине. Для более тщательного анализа произведем распределение студентов по величине рейтинга тенденциями в своих достижениях, преподаватель может скорректировать образовательный процесс с целью достижения наибольшей его эффективности.

Далее на основе спрогнозированных значений построим векторные поля тенденций в индивидуальных учебных достижениях студентов учебной группы. Рассмотрим три поля векторов, соответствующие трем этапам прогнозирования (рис. 2–4).

Знаки тенденций достижений учащихся

№	Ф.И.О.	Факт	Тренд	Знак тенденции
1	Иванова Татьяна Валентиновна	3,20	–1,16
2	Белогорцев Юрий Андреевич	6,30	–4,00
3	Симашева Карина Андреевна	18,00	–8,86
4	Зарипова Гузель Наилевна	19,00	–4,80
5	Мустаева Гульнара Маратовна	19,70	–4,60
6	Раздьяконов Вадим Александрович	21,40	–5,20
7	Жуков-Дуккарт Антон Игоревич	21,50	–2,70
8	Абзанова Юлия Дамировна	25,00	–7,90
9	Краснов Александр Валерьевич	27,10	–6,20
10	Кучарова Эльмира Илдаровна	32,60	2,80	+
11	Батталова Вероника Игоревна	34,00	–0,18	-
12	Шаймарданов Самат Раильевич	39,70	–5,44	-
13	Легковой Станислав Вячеславович	40,30	1,28	+
14	Гизатов Кайдар Русланович	41,50	–2,10	-
15	Новокшонова Дарья Юрьевна	43,90	–2,14	-
16	Лабукин Михаил Васильевич	49,40	1,50	+
17	Галяутдинова Эльвина Райхановна	61,00	3,50	+
18	Габдуллина Динара Ринатовна	64,30	–4,80	-
19	Ибрагимова Айгуль Азатовна	66,40	–0,59	-
20	Байназарова Дина Ириковна	66,70	1,70	+
21	Ишаева Алия Якубовна	69,80	3,80	+
22	Насибуллина Регина Ринатовна	81,60	11,70
23	Гильманшина Карина Айдаровна	95,50	2,22
24	Николаев Руслан Владимирович	96,00	2,94

Направление каждого вектора соответствует направлению линейного тренда. Модули векторов, очевидно, должны интерпретировать силу мотивации студентов как положительную, так и отрицательную. Предлагается в качестве модулей векторов принять значение коэффициента аппроксимации тренда (рис. 5). Обоснованность данного предложения следует из того факта, что чем меньше разбросанность данных, тем сильнее выражена мотивация к успешности образования, и, соответственно, чем больше разброс эмпирических данных, тем более нестабильно данное направление изменения и, следовательно, менее четко выражена тенденция. Далее, действуя по правилам операций над векторами, произведем сложение векторов, приводя их в точку графика, соответствующую среднему значению группового рейтингового балла и вычислим равнодействующую векторов тенденций (пунктирный вектор) (рис. 6).

Данная равнодействующая определяет вектор направленности успешности образования всей учебной группы в целом и соответственно является интегральным информационным ориентиром для преподавателя.

Отметим, что в данном случае рассматривается не простая сумма векторов в декартовой системе координат. Каждый индивидуальный вектор, с одной стороны, является носителем прогнозной информации, полученной на основе нейронной сети модели, а с другой, – носителем степени стабильности данной информации, полученной на основе статистических методов обработки информации. Таким образом, каждый подобный вектор тенденции характеризует синтез направленностей студента в освоении учебного материала с силой мотивации, стабильности в этих достижениях.

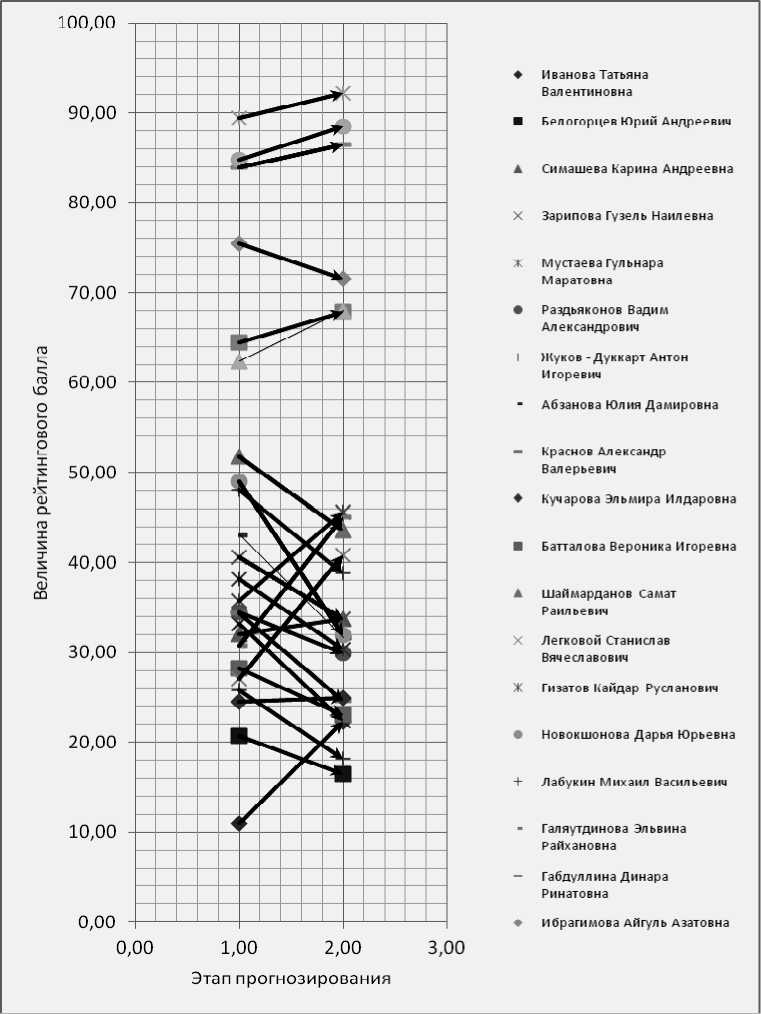
Рис. 2. Векторы индивидуальных тенденций успешности образования на I этапе прогнозирования

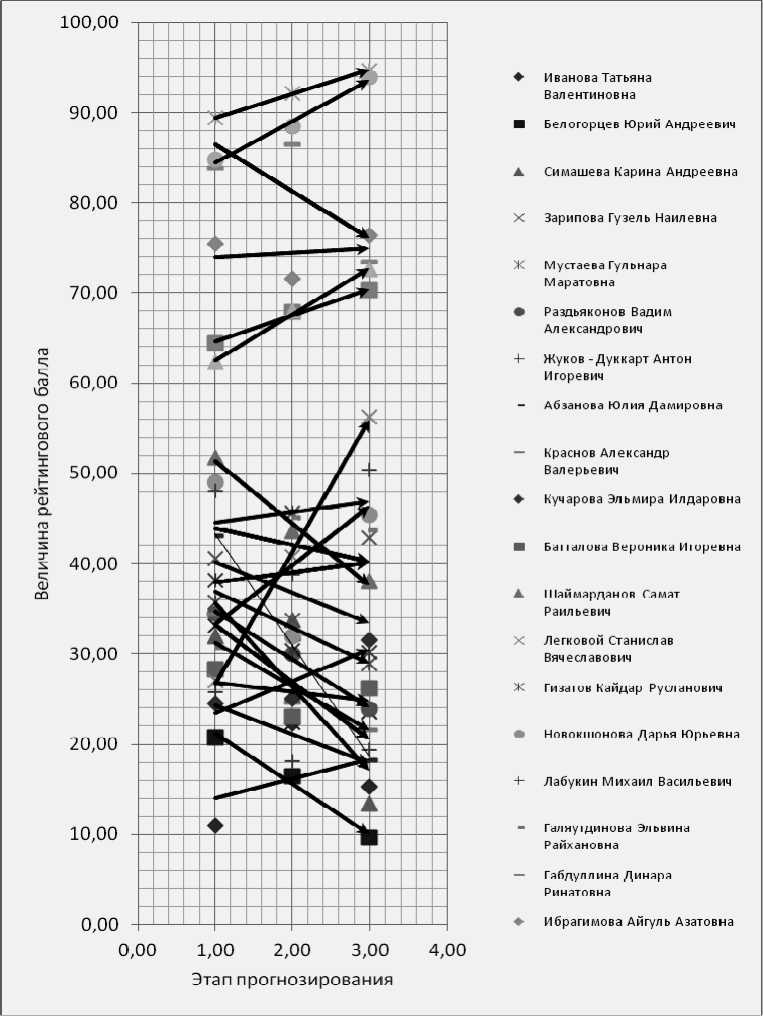
Рис. 3. Векторы индивидуальных тенденций успешности образования на II этапе прогнозирования

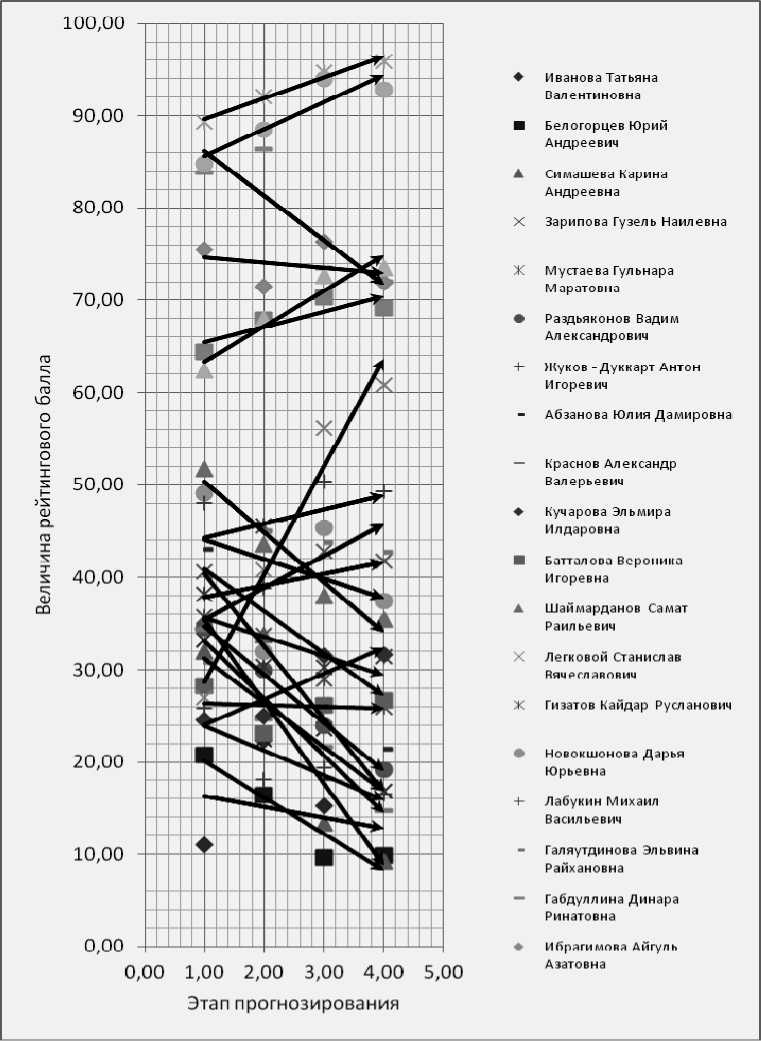
Рис. 4. Векторы индивидуальных тенденций успешности образования на III этапе прогнозирования

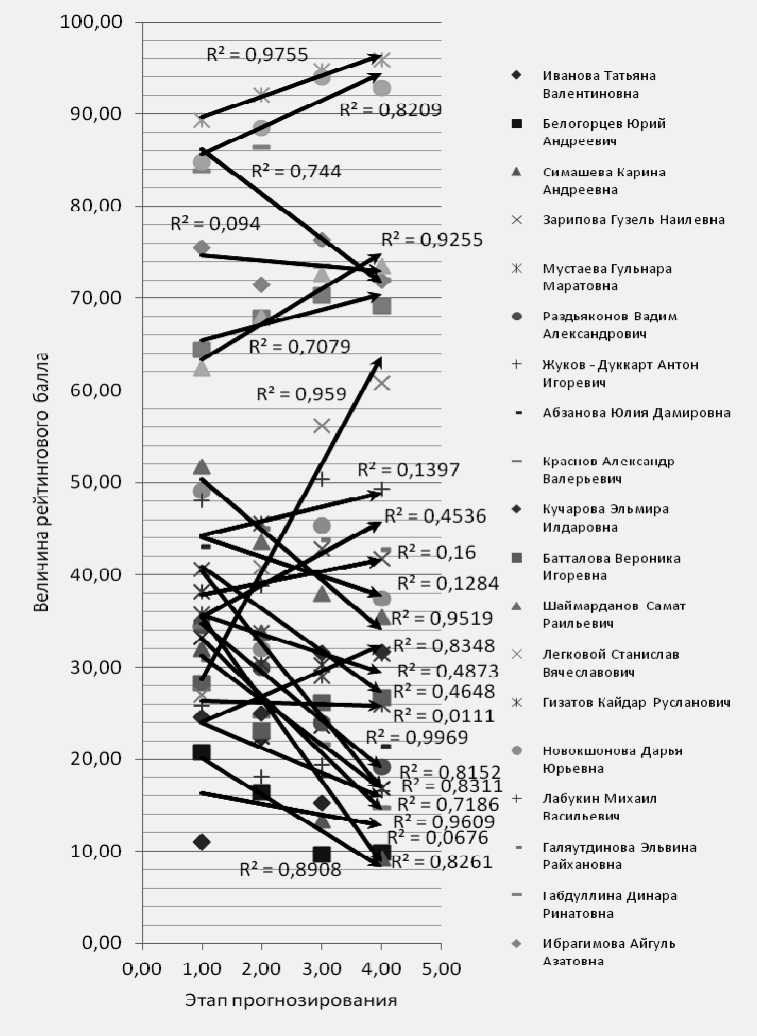
Рис. 5. Мера достоверности векторов индивидуальных тенденций успешности образования на III этапе прогнозирования

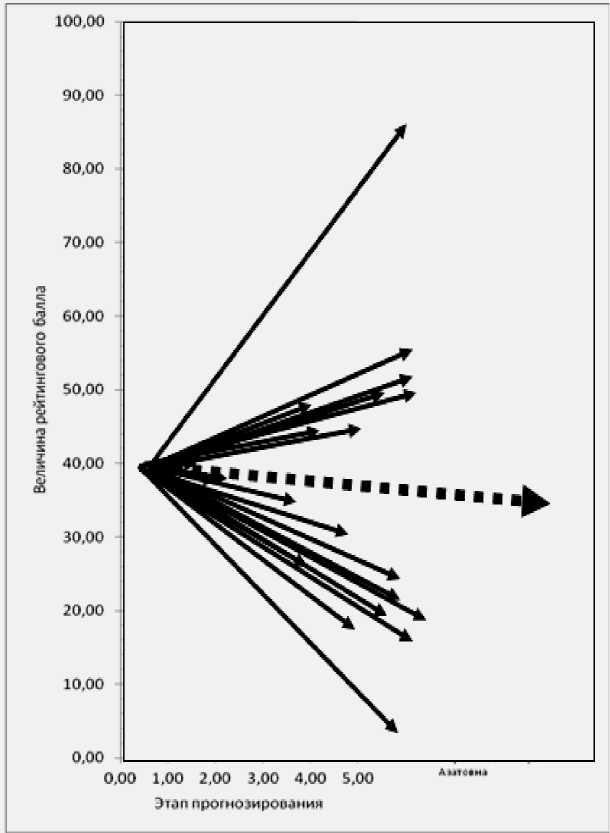
Рис. 6. Результирующий вектор векторов индивидуальных тенденций успешности образования на III этапе прогнозирования

Отметим, что колебания прогнозных значений не являются погрешностями прогнозирования НС модели, а скорее представляют отклик данной ассоциативной модели прогноза на нестабильность достижений самого студента - чем меньше стабильность, тем сильнее разброс прогнозных значений. Отметим, что в идеале погрешность таких разбросов в прогнозных значениях падает, но принципиальный факт их существования состоит в том, что меньшая стабильность в рейтинговых достижениях студентов рождает больший разброс в их индивидуальных прогнозах, и это не является слабым местом в НС моделях прогнозирования. Данная особенность является другой характеристикой НС модели прогнозирования - диагностической [6]. Заметим, что в данном случае речь идет о соответст- вующим образом обученной НС модели [3], так как в противном случае, очевидно, прогнозы не могут являться достоверными. Выделяя подгруппу индивидуальных нестабильных прогнозов, мы, тем самым, выделяем подгруппу нестабильно работающих студентов. Далее, производя коррекцию учебного процесса именно по отношению к студентам этой подгруппы, можно добиться более стабильной их работы, с последующим проявлением эффекта повышения результатов их обучения.

Отдельным пунктом стоит работа со студентами, показавшими устойчивую отрицательную тенденцию к освоению материала. Первоначально необходимо разобраться с возможными причинами данной тенденции применительно к каждому студенту, которых может быть достаточно много. Затем, выбрав соответствующую стратегию коррекции, воздействовать на данный контингент учащихся.

Изменение группового вектора успешности обучения в соответствии с этапами НС прогнозирования носит характер корректирующего воздействия преподавателя на данную учебную группу. Интерпретация индивидуальных прогнозных данных как векторов тенденций позволяет одновременно учитывать и индивидуальные особенности студентов и общее направление образовательного процесса в группе.

Таким образом, предлагаемая методика дифференциации позволяет разделять множество студентов на подмножества по признаку направленности и силы тенденций к изучению учебного материала. Подобная дифференциация позволяет скорректировать образовательный процесс, используя адресный поход к студентам. Построение же результирующего группового прогнозного вектора позволяет определить общую направленность успешности образования студентов учебной группы и при необходимости внести изменения в текущий образовательный процесс.