Диффузионная модель перемешивания сливочно-растительных спредов

Горбатова А.В., Шендрик Т.А., 2015

Одной из основных стадий производства сливочно-растительных спредов является эмульгирование. Качество готового продукта и возможность его длительного хранения определяется условиями получения стабильных эмульсий. При реализации этой стадии необходимо учитывать, что излишнее механическое воздействие может привести к дестабилизации жировых эмульсий, а также требует дополнительных затрат энергии [2, 3, 5]. Поэтому определение продолжительности перемешивания спредовых композиций до достижения однородности является актуальной задачей технологии их производства.

Продолжительность процесса перемешивания можно определить по поведению частиц трассера, вводимого в перемешиваемую среду. Необходимо, чтобы частицы трассера имели одинаковую плотность с окружающими их объемами жидкой фазы. В этом случае траектории движения частиц трассера и жидкости совпадают, а степень однородности перемешиваемой композиции можно рассчитать через коэффициент вариации, определяемый формулой:

В этом случае геометрия аппарата не имеет значения и можно рассматривать задачу как одномерный перенос частицы трассера в плоском слое перемешиваемой жидкости (рисунок 1):

^{д n (} x^{, т} )      ^{д 2} n ⁽ x^{, т} )

дт           дx2    ’ n (x ,0) = 0,(3)

^^ = 0 ,(4)

д x

D Mhr) = jо [1(т) _ 1(т — то)],(5)

дx где τ – время, с; n – счетная концентрация частиц в объеме жидкости, шт/м3; D – эффективный коэффициент перемешивания, м2/с; T — продолжительность ввода частиц трассера в жидкость, с; x - координата, м; 1(т) - функция Хэвисайда; j – средняя штучная плотность поверхностного потока частиц за время их ввода т0, шт/(м2-с).

По определению:

К

var

m

Z ^{( n}i - n )

i=1________________ m -1

z j о =      ,

⁵ "^т о

где n – средняя по объему перемешиваемой среды концентрация частиц трассера; n – их локальная концентрация в m точках, равномерно распределенных по всему рабочему объему аппарата.

Локальные концентрации трассера определяются закономерностями движения жидкой фазы. Если для описания ее поведения использовать уравнения движения Навье-Стокса в общей постановке, то в силу их нелинейности принципиально невозможно получить решение задачи в аналитическом виде. Различные упрощающие допущения как, например, модели перемешивания, предусматривающие разбиение потока на области с восходящим и нисходящим движением жидкости, неприменимы в данном случае, т. к. не отражают в полной мере трехмерный характер течения перемешиваемой среды.

Высказано предположение о том, что интенсивность перемешивания, одинаковая по всему объему жидкости, позволяет воспользоваться диффузионными представлениями о характере протекания процесса [1].

где z – общее количество вводимых частиц, s – площадь свободной поверхности жидкости.

Пусть n₀ = z IV - средняя по объему жидкости концентрация частиц. Тогда z = nV и с учетом (6):

_ n 0 V _ ⁿ о h

J 0 =     =

⁵ • ^т о     ^т о

Принимая во внимание (7), граничное условие (5) примет вид:

D ^ = n o h _{[ 1 (} т ) _ к т _ т 0 ) ] .   (8)

д x      т₍

Приведем систему уравнений (2-4), (8) к безразмерному виду:

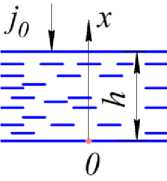
Рисунок 1. Расчетная схема

д N ( X ,Fo) _ д ² N ( X ,Fo)

дРо   =    дX2    ,( )

N (X ,0) = 0,(10)

5N<0iPo>=о,(ii)

дx,

^Щ0) = -^ [1(po)- 1(ро-ро0)],(12)

д-X      Ро₀

где N = n I n ₀, Fo = D т I h ², Fo₀ = D ^ I h ², X = x I h .

Применим к системе уравнений (9)-(12) одностороннее преобразование Лапласа по переменной Fo:

d ² N_L ( X , 5 )

5 • N (X, 5) =-----L '

dX1

dN (0,5) =0 dX dNL (1,5) _ 1   1 - exp(-5Fo0)

dX    Fo0

где 5 и N_l ( X , 5 )  - изображения Fo и

N ( X ,Fo) .

Решение задачи (13)-(15) в изображениях имеет вид:

N l ( X , 5 ) = -¹- ^Foo

[ 1 - exp( - 5 Fo₀) ] ch( V s • X )

. (16)

5-Js • sh ( V $ )

Используя теоремы обращения Ващенко-Захарченко и осуществляя переход от изображений к оригиналам функций в (16), получаем решение задачи в виде:

N(X,Fo) = 1 - — TT Cos(^”X) x

^Foo n = 1 M_n^cos Ц п         (17)

^{x ex} p ^{( -} ^ 2^Fo) [ 1 ^{- ex} p ⁽ ^ 2^Foo ) ]

Изменение безразмерной концентрации частиц трассера, рассчитанной по формуле (17) для начала процесса перемешивания, представлено на рисунке 2. Зависимость концентрации от времени была уточнена по высоте перемешиваемого слоя жидкости (рисунок 3).

В верхней половине перемешиваемого слоя (рисунок 3) объемная концентрация частиц проходит через максимум. Это связано с перемещением вниз за счет конвективного перемешивания вводимых импульсно частиц трассера. В нижней части слоя концентрация монотонно возрастает до единицы, что соответствует физическому смыслу задачи.

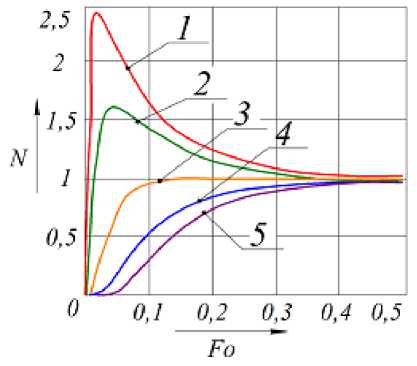
1 – Х = 0,8; 2 – Х = 0,7; 3 – Х = 0,5;

4 – Х = 0,3; 5 – Х = 0,1

Рисунок 3. Изменение объемной концентрации частиц трассера по высоте перемешиваемого слоя

Отбирая пробу продукта в определенной точке перемешиваемого слоя в различные мо- менты времени, получаем экспериментальную зависимость безразмерной концентрации частиц от числа Фурье N3Kcn (Х, Fo). С ее помощью можно рассчитать коэффициент эффективного перемешивания, используя следующий алгоритм.

Задаются произвольным значением коэффициента эффективного перемешивания D ,

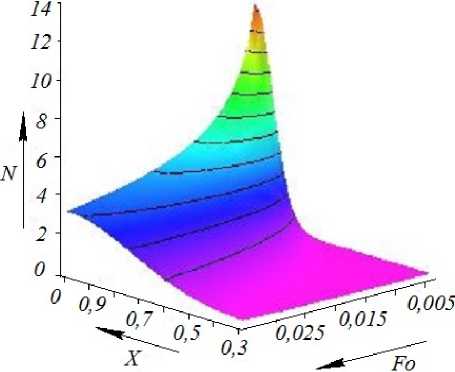
Рисунок 2. Изменения объемной концентрации частиц трассера в начале процесса перемешивания

рассчитывают соответствующую величину безразмерной продолжительности ввода им-

DT пульса частиц трассера Fo0 = —^, а также без-o    h2

D^- размерное текущее время процесса Fo = —у i     h ²

( т - размерное текущее время, с).

Экспериментальное значение безразмерной концентрации частиц трассера находят по формуле:

Nэксп = nпр / П0 , где ппр = znp / Vnp - счетная концентрация частиц трассера в пробе, zпр – количество трассеров в пробе, шт; Vпр – объем пробы перемешиваемой жидкости, м3.

Минимизацией функционала г Г Nрасч (0,96;Fo i) - Nэксп (0,96;Fo ,)

V [          N расч (0,96;FO i )

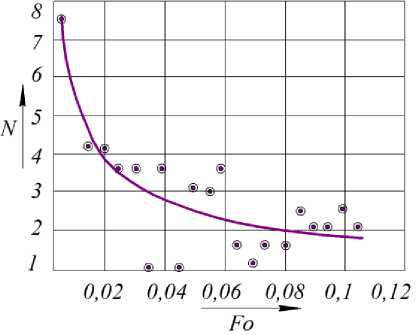
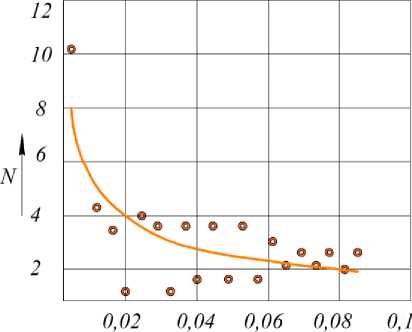
где N расч (0,96;Fo i ) находили по (17), с использованием экспериментально полученных данных (рисунки 4-5), были идентифицированы значения коэффициента эффективного перемешивания для различных условий проведения процесса.

Процесс получения сливочно-растительных спредов складывается из двух стадий: перемешивание при температуре 65 °С; процесс кристаллизации при температуре от 30-15 °С. Для оценки коэффициента эффективного перемешивания в зависимости от числа Рейнольдса мешалки [4] в исследованном интервале изменения параметров процесса получения спредов предложены соотношения:

• -    для процесса перемешивания:

D = 3,5 - 10 ^{- 13} - Re² - 1,8 - 10 ^{- 9} - Re + 3,7 - 10 ^{- 6}; (19) - для процесса кристаллизации:

D = 1,8 • 10 ^{- 10} - Re² - 2,1 - 10 ^{- 8} - Re + 1,2 - 10 ^{- 6} .(20)

При анализе процессов перемешивания обычно рассматриваются две взаимосвязанных задачи:

• -    определение продолжительности перемешивания до получения продукта заданной однородности;

• -    определение однородности продукта при заданной длительности процесса перемешивания.

Указанные задачи могут быть решены с использованием временной зависимости для коэффициента вариации, характеризующего однородность перемешиваемой системы согласно уравнению (1).

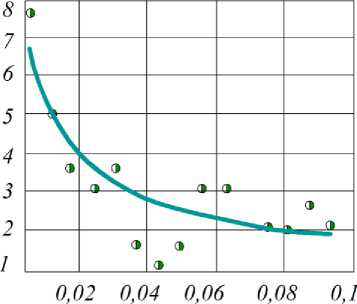
Но

в а - спред № 1, п = 150 мин-1, D = 2,29-10-6 м2/с; б - спред № 3, п = 140 мин-1, D = 1,82-10-6 м2/с; в - спред № 2, п = 130 мин-1, D = 1,49 -10—6 м2/с

Рисунок 4. Сравнение результатов эксперимента (точки) с расчетом по (17) (линия) процесса перемешивания

а

б

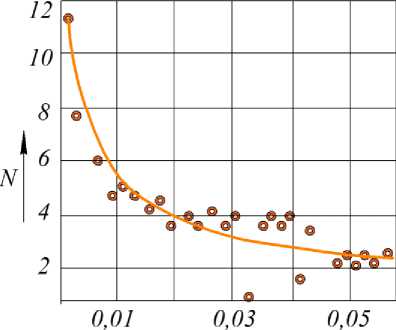
Fo

в

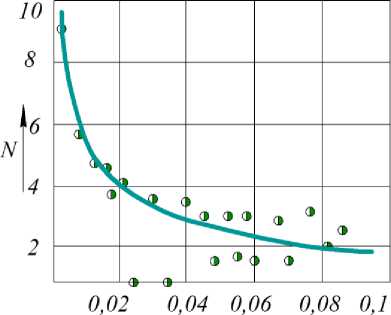
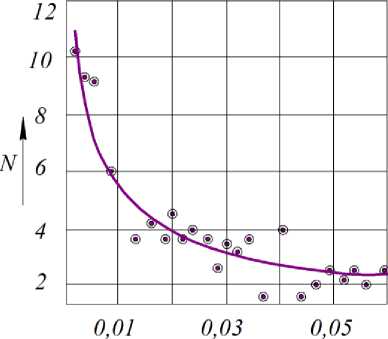
а - спред № 1, п = 150 мин^-1, D = 0,954 - 10 — 6 м²/с;

б - спред № 3, п = 140 мин^-1, D = 0,617 - 10 6 м²/с; в - спред № 2, п = 130 мин^-1, D = 0,586 - 10 ^{- 6} м²/с

Рисунок 5. Сравнение результатов эксперимента (точки) с расчетом по (17) (линия) процесса кристаллизации

Переходя в правой части уравнения (1) к безразмерным величинам, получаем следующую расчетную формулу для коэффициента вариации, которая учитывает его изменение как по высоте слоя жидкости, так и по времени:

N (Fo) = 1 -

2      ^ [sin⁽ ^ n^Xк ) ^{- sin(} M n X н )] _х

^Fo 0 ⁽ X к ^- Х н ) n = 1        A 3 • cos M n

X exp^{( -} A 2 ^Fo) • [1 ^- exp⁽ A ^2Fo 0 ) ]

^К var

m

Е m - 1 i = i

N £W _ Л²

N (Fo)     _

.

Здесь m – число точек разбиения отрезка [ X н , Х к ] , для которого среднее по его длине значение концентрации частиц трассера определяется выражением

Определим коэффициент вариации в конце процесса перемешивания спреда № 1 при n = 150 об/мин. Безразмерная длительность процесса составляет Fo = 0,0935. Этому значению числа Фурье согласно соотношениям (17) и (21) соответствует К,^ = 3,2 %, что свидетельствует о достаточно хорошей однородности получаемой спредовой композиции.

Используя данный способ, можно оценить однородность продукта в любой момент времени.

Вестник ВГУИТ, №3, 2015