Динамическая и химическая трансформации сталкивающихся облаков H I

В последние годы в связи с развитием технологий мониторинга околоземного космического пространства и резким ростом обнаруженных потенциально опасных для Земли астероидов проблема астероидно–кометной угрозы стала серьезно осознаваться человечеством. Примером реальной опасности могут служить события, произошедшие 15 февраля 2013 г., когда астероид 2012DA14 прошел в опасной близости от Земли на расстоянии меньшем радиуса геостационарной орбиты, а Чебаркульский суперболид вошел в атмосферу и взорвался над Челябинском.

Время подлета астероида от геостационарной орбиты до поверхности Земли составляет 20–40 минут при скорости в 30–60 км/с. В такой ситуации время на обнаружение и защитные действия крайне ограничено, что стимулирует разработку систем космической защиты, размещенных в космосе в окрестности Земли и содержащих средства обнаружения и поражения быстро движущихся опасных космических объектов (БДОКО).

При определении положения БДОКО необходим быстрый и точный прогноз его траектории для вычисления точки встречи средств поражения с объектом. Очевидно, что на заключительном этапе сближения с объектом должны оперативно измеряться параметры движения астероида радиолокационной системой (РЛС), расположенной на самих средствах поражения, работающих в режиме самонаведения. Прогноз траектории производится по измерению скорости объекта на основе анализа доплеровского сдвига частоты отраженного радиолокационного сигнала. Необходимым условием эффективной работы РЛС космической защиты является повышение точности и скорости измерения частоты доплеровского сигнала. Неточность в определении параметров движения объекта приведет к срыву операции по его уничтожению, учитывая разность скоростей астероида (> 30 км/с) и средства поражения (~ 10 км/с).

В работе [3] предлагается использовать алгоритм оценки радиальной скорости космического тела в течение времени прихода доплеровского сигнала (то есть без дополнительной спектральной обработки) с помощью дробнодифференцирующего фильтра. В настоящей работе мы приводим оптимальную схему работы аналогового дробнодифференциру-ющего фильтра для сверхбыстрого оценивания положения центра тяжести спектра отраженного доплеровского сигнала.

Процедура дробного дифференцирования порядка Ѕ представляет собой интег- ральное преобразование сигнала x(t) в реальном времени вида

D¹ ' ² x ( t ) = F - {V T ^ F [ x ( t ) ] } ,             (1)

где F[x(t)] – спектральная плотность амплитуды сигнала, щ– частота, j – мнимая единица, а формула (1) определяет свертку входного сигнала с импульсной характеристикой фильтра h (t) = F-1{j

Дробная производная Римана-Лиувилля порядка S определяется по формуле [2]:

1/2 d t x ( t ') dt'

^D x ⁽ t )= dt ¹ VT-7 ’      ⁽²⁾

всякую линейную операцию, выполняемую над функцией, в том числе операцию вычисления дробной производной, можно представить как свертку функции с импульсной характеристикой:

D ^1/2 x ( t ) =     h ( t ') x ( t - 1 ') dt ' .           (3)

-to

Импульсная характеристика дробно– дифференцирующего фильтра порядка 1/2, впервые полученная в работе [1], имеет вид

h ( t ) = d-q(( t ) + lim _e ^₀-^ dt            P

д ⁽ t )      y ⁽ t )

- --- v t+ e  2( t + e)2

, (4)

где д( t ) есть дельта-функция Дирака, y ( t ) – функция Хевисайда.

Аналоговый фильтр строится на аппроксимации импульсной характеристики (4) набором из N затухающих экспонент, каждая из которых отвечает импульсной характеристике некоторого звена первого порядка, что подразумевает возможность аппаратной реализации аналогового фильтра набором стандартных радиотехнических звеньев первого порядка. Фактически задача сводится к нахождению при фиксированном значении аппроксимации наивысшей степени точности степенной составляющей импульсной характеристики (4), которая при обезразмеривании времени на шаг дискретизации по времени e имеет вид

H ( t ) =-----3

( t + 1) 2

Аппроксимирующая функция представляет собой конечную сумму вида

H N ( t ) = Z N = , b k=~" ' ,         (6)

содержащую 2 N неопределенных коэффициентов а_k и b_k . Предложена оптимальная аппроксимация (6), построенная на квадратуре наивысшей степени точности. На рисунке 1 приведены в логарифмической шкале графики временной зависимости аппроксимируемой функции H ( t ) (верхняя кривая) и аппроксимирующих функций H ^~ _N ( t ) , последовательно приближающихся к H ( t ) при N = 6, 10, 14, 16, 18.

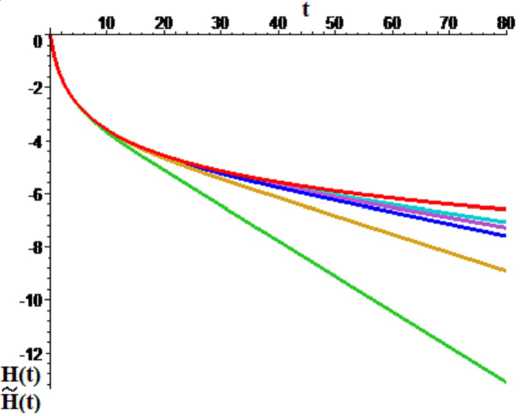
Рис. 1. Графики аппроксимируемой функции H ( t ) и аппроксимирующих функций H ^~ _N ( t )

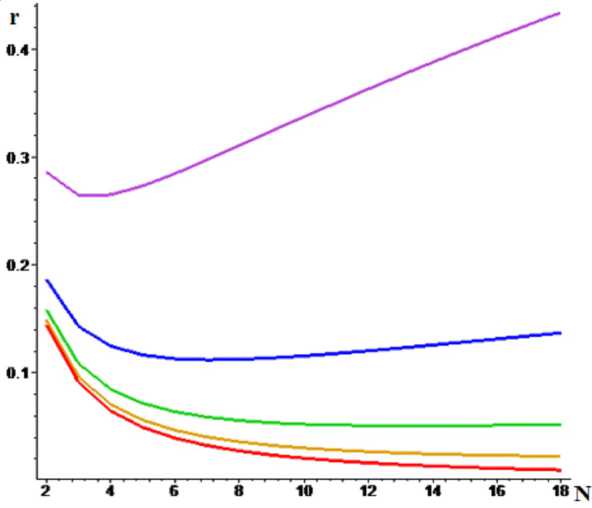
Рис. 2. Графики функций полных погрешностей r_N . Нижняя кривая соответствует среднеквадратической погрешности R_{N .} Снизу вверх расположены кривые, соответствующие погрешностям прибора p = 0.003, 0.01, 0.03, 0.1.

Мерой точности аппроксимации может служить среднеквадратическая погрешность to                                           to

R n =A 1 (( H ( t )- H ~ N ( t )) 2 dt Ч H ( t) 2 dt . (7) 00

Расчеты показывают, что R_N убывает с ростом N , но стремление к нулю относительно медленное в силу того, что экспоненты убывают быстрее чем любая степень. Те же расчеты свидетельствуют, что для достижения общепринятой в радиотехнике точности в 1 % (то есть R_N = 0.01) необходимо взять N = 18 звеньев. Надо иметь в виду, что звенья, составляющие реальный фильтр суть устройства, обладающие погрешностями, обусловленными неидеальностью изготовления этих устройств. Составлять фильтр из такого большого количества элементов в N = 18 невыгодно, так как на практике начнет накапливаться погрешность, вносимая каждым элементом в отдельности.

Пусть каждое звено характеризуется относительной погрешностью изготовления прибора p. Естественно ожидать, что суммарная погрешность, вносимая N элементами, должна определяться как статистическая погрешность, пропорциональная корню из числа элементов. Тогда суммарная погрешность фильтра есть to                                           to rN 4 1 ((H(t)-11N(t))2dt/£ H(t)2dt + P^N, (8) 00

На рисунке 2 представлены графики полной погрешности r_N . Если допустимая погрешность прибора составляет p = 0.01, то, как следует из рисунка, минимум полной погрешности как функции числа звеньев достигается примерно при N = 12. Минимум при этом пологий, и это значит, что при уменьшении количества звеньев погрешность изменится незначительно. Отсюда следует, что при почти той же точности аппроксимации экономически более выгодно составлять фильтр из 6–8 элементов.

ПРИМЕЧАНИЕ волновых процессов и радиотехнические системы. – 1999. – Т. 2, №3–4. – С. 39–41.

• 2.    Samko, S. Fractional integrals and derivatives / S. Samko, A. Kilbas, O. Marichev // Theory and Application. – Gordon & Breach Sci. Publishers, 1993.

• 3.    Zakharchenko, V. D. On protecting the planet against cosmic attack: ultrafast real-time estimate of the asteroid’s radial velocity / V. D. Zakharchenko, I. G. Kovalenko // Acta Astronautica. – 2014. – Vol. 98C. – P. 158–162.

APPLICATION OF A FRACTIONAL DIFFERENTIATION FILTER FOR ULTRAFAST ESTIMATION OF MOTION VARIABLES

OF HAZARDOUS ASTEROIDS

Kazankova Ekaterina Arkadievna